2017年高考数学全国卷I试题和答卷分析

华南师范大学数学科学学院(510631) 刘秀湘

2017年高考数学全国卷I试题和答卷分析

华南师范大学数学科学学院(510631) 刘秀湘

2017年数学科全国I卷(乙卷)(后文简称“全国卷”或“试卷”)遵循考试大纲的各项规定,坚持能力立意的命题原则,渗透数学文化,体现了对“核心素养”的考查,体现了数学的科学价值和理性价值.简约而不简单,深刻但不深奥,有利于高校选拔优秀人才,有利于引导中学数学教学.本文就2017年高考数学试卷的试卷设计、试题特点和考生答卷情况进行分析,希望有助于高中数学教学及今后的高考备考.

一、试卷设计分析

2017年的高考文、理科试卷的题型与分数与往年相比略有调整,选做题由三选一改为二选一,其他与往年基本保持一致.高中数学的主干内容函数与导数、数列、三角、立体几何、解析几何和概率与统计等6大知识板块的分值在文、理科试卷中的分值分别达到125分、120分,体现了主干内容重点考的试卷设计思路.表一、表二分别为2017年高考数学文科、理科考查内容与分值分布:

表一2017年高考数学文科考查内容与分值分布

表二2017年高考数学理科考查内容与分值分布

2017年全国卷从学科整体意义和数学素养的高度立意,淡化特殊技巧,加强针对性,有效地检测考生对数学知识中所蕴涵的数学思想方法的掌握程度.在试题的命制上,各题目不仅注意了知识考查的水平要求有层次性区分,还侧重基础知识和基本技能的考查,注重考查逻辑推理能力、运算能力、数学思想方法、应用能力、创新能力,强调对数学本质的理解.表三、表四是文、理科试卷的数学知识目标结构:

表三2017年数学知识目标结构（文科卷）

表四2017年数学知识目标结构（理科卷）

二、试题的特点分析

2017年高考数学全国I卷试题难度适中、稳中求变、导向明确,体现了基础性、综合性、应用性和创新性,没有偏题怪题,考查通性通法.具体体现了以下几个特点.

(1)突出数学思维学科特点,强化理性思维考查

2017年修订后的数学科考试大纲削枝强干,加强主体内容,强调理性思维.2017年高考充分发挥数学思维学科的特点,加强理性思维的考查,把考查逻辑推理能力作为命题的首要任务,运用数学知识作为载体,考查考生缜密思维、严谨推理能力.

首先,考查考生运用数学公式的严谨性,如文科第17题运用等比数列求和公式时要分析公比是否为1,文、理科第20题要求考生掌握使用韦达定理的前提是判别式Δ≥0;其次,运用数形结合考查严谨性,如理科第18题,利用向量法计算出夹角的余弦值后(根据所选的法向量,可能是正,也可能是负值),要根据所给的立体图形判定二面角A−PB−C是否为钝角,才能得到正确的答案是负值(如果改为求正弦值,则不会有正负号的选择问题);最后,利用分类讨论考查数学推理的严谨性是经典的题型,但2017年的试卷除了第21题是标准的分类讨论外,在两道选做题都设置了参数,考查分类讨论.

(2)考查数学阅读能力,强调数学语言的表达

社会越来越数字化,对数学阅读与表达能力的要求将会越来越高,数学阅读与表达能力是学生学会数学学习(自学)的基础能力,2017年试题从两方面加大了数学语言能力的考查.第一是数学语言的阅读,文科第19题题干部分的文字、标点和数学式子(含字母)一共716个,理科是640个,试题占所在卷页面的三分之二！考生在阅读审题时对常用的数据公式及其意义应了然于心,从而能够尽快从冗长的文字、标点和数学式子(含字母)中得到有用的解题信息.第二是数学语言的表达,如文科第17题要求考生能够正确用综合法方式或者分析法方式书写结论,文、理科第19题第(2)问第(i)小问更是要求考生能够用数学语言表述何为生产过程中出现异常情况以及此时进行检查的合理性.

(3)考查通用数学方法,凸显创新性

2017年试卷加强基础性和创新性,以数学基础知识、基本能力、基本思想方法为考查重点,注重对数学通性通法的考查.考查时从学科整体意义和思想价值的高度立意,淡化特殊技巧,加强针对性,有效地检测考生对数学知识中所蕴涵的数学思想方法的掌握程度.试题在命制时充分考虑到考生数学能力的个体差异,绝大多数试题的解答方法、思维方式不是唯一,而是一题多解,给考生提供了较大的发挥空间.如文科第4题,理科第2题是渗透我国传统文化的一道试题,可以结合四个选择答案,根据对称性和圆面积的计算容易发现概率是小于且与圆面积公式πr2有关,故答案为.文科第6题问得是直线AB与平面MNQ不平行的图形,“正难则反！”,观察图形,可以发现B,C,D四个选项都是平行的,利用排除法选A!文、理科第19题特别考查了运算技巧,要计算剔除离群值后零件尽寸的均值和标准差,快捷的做法是利用题目所给的数据进行运算,但有些考生不懂变通,死记公式,用题目中的15个数据重新计算平均值和方差,耗费大量时间而且容易算错.这样通过方法的选择、解题时间的长短,甄别出考生能力的差异,达到精确区分考生的目的.

三、考生答卷情况及反映的问题

从评卷情况来看,存在的主要问题有:数学语言的阅读与表达能力薄弱,书写不规范,推理论证严谨性不够,运算技巧有待提高.从考生的具体答题情况来看,除了文科第20题,21题外,其它文、理科解答题的0分卷均未超过50%,明显好于去年.但是理科第17题得分出人意料,该题考查解三角形,主要涉及正、余弦定理以及三角变换,这道题本来是容易的解答题,但得分甚至低过第18题立体几何题.解答中的主要问题一是考生没有正确理解正弦公式“边角互换”的本质,想当然地将sinA换成a.二是不能从众多的三角变换公式中选择适合本题的变换,导致复杂的运算出现错误.理科第19题的平均分甚至低过文科,反映出理科考生一方面对冗长的文字阅读不适应,另一方面对正态分布这个知识点的掌握不到位.文科第17题这道看似简单的试题在数学表述的严谨性方面要求很高.文科第18题得分比去年提高较多,第19题的解答比理科也要好.

选做题方面,考生选做22-23题的人数比例如表五.从表中可以看出,绝大部分考生都是选做第22题.但是两道选做题得分比去年均有所下降,主要是试题中出现了含参数分类讨论的问题.

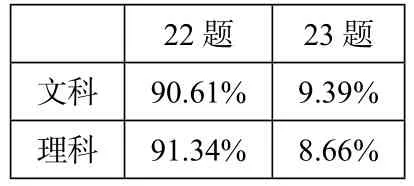
表五选做题各题选做人数百分比

文、理科试卷抽样平均分如下表.

表六2016-2017年文、理科各题抽样平均分

与2016年相比,文科选择、填空题、第18,19,20题的得分都上升,理科除了第18题、21题外,其他题目的得分都低于去年,这是出乎很多师生的预料,其中原因值得引起重视.文、理科试卷难度分别为0.38,0.50.考生主观题答卷典型错误及分析情况如下.

(一)文科卷

题 号典型错误原因分析13题−1 2,−2未区分向量平行,垂直时内积关系,计算出错14题y=3x−1对y=x2+1 x在(1,2)求导时,对 1 x求导出错,少了“−”号y=2x 对y=x2+1 x在(1,2)求导时,对x2求导出错15题1随便猜测3√2 2计算出错16题4π估计的半径为1 16π估计的半径为2 17题用Sn= a1(1−qn)1−q时，忽略了q1条件对公式理解片面证明等差数列的充分条件与必要条件混乱对等差数列的概念理解不够清晰,等差数列的判定与性质混淆导致逻辑不清指数函数的运算出错运算过程中观察不仔细,对数列的项数不理解书写不规范,如 (−2)n写成−2n初中开始对指数、幂的书写不规范养成了这种错误的书写习惯18题第一问直接由AB⊥AP,CD⊥PD推出平面PAB⊥平面PAD.线面垂直,面面垂直的判定定理不清楚

题 号典型错误原因分析18题不 会 将 ∠BAP =∠CDP=90°转化为AB⊥AP,CD⊥PD不会作几何的基本推理直接由AB⊥AP推出AB⊥平面PAD.错用线面垂直的判定定理不会证明或不能准确计算四棱锥P−ABCD的高PE逻辑推理能力和计算能力不足,尤其是在计算高PE的时候不善于将立体几何问题“平面化”符号表述错误,如AB∈平面PAB,等.数学表述不规范第一问推出AB⊥AP，CD⊥PD，不会继续推理与证明或乱推理逻辑推理能力差矩形ABCD的面积和四棱锥P−ABCD的侧面积计算错误计算能力不足和概念不清楚.19题■(∑16i=1x2i−162)≈0.212看错,忽略连加号前的1 16;=1 16,而非=1 16∑16 i=1xi概念不清,数学符号认识不清,观察能力不强,计算代入出错不理解“若|r|＜ 0.25,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小”对题目题意理解不清未用已知数据进行数据,作无用功运算技巧掌握不好20题k = x2−x1y2−y1或x2+x1y2+y1或 y2+y1x2+x1等未记住两点间的斜率公式利用特殊点求斜率,例k=94−1 4 3−1=1点A,B为曲线C上两动点利用特殊直线求斜率,例直线AB过焦点F 动直线AB不一定过焦点F x2+x1=8或|x2|+|x1|=4或x1−x2=4审题错误或书写错误未求出点M的坐标不会将M的坐标与相切问题联系起来未求出x1x2,y1y2,y1+y2的值不会将x1x2,y1y2,y1+y2与韦达定理联系起来−−→AM ·−−→BM=x1x2+y1y2−(y1+y2)2−−→AM ·−−→BM=x1x2+y1y2−(y1+y2)2−3计算出错21题求导错误 1:f′(x)=e2x−aex−a2求导公式不熟练求导错误 2:f′(x)=2e2x−aex−2ax 求导对象不清晰求导错误 3:f′(x)=2ex2−aex−a2指数运算有误或者表达符号有误

题 号典型错误原因分析22题■■ ■■x+4y−3=0 x2+9y2=9仅得1解(3,0)由25y2−24y=0即得y=0■■■ ■x+4y−3=0 x2+9y2=9求解出错由25y2−24y=0两边除以y■■ ■■x+4y−3=0 x2+9y2=9得到2个错解或0个解把y=−1 4x+3 4代入消元,计算繁琐,得2个错解或0个解由|5sin(θ+ φ)− a−4|max=17得|−5−a−4|=17,a=8或a=−26认为−a−4= −(a+4)是负的不懂得验根,增根不知舍去由|5sin(θ+ φ)− a−4|max=17得|−5−a−4|=17,a=−16或a=18把a看成了常数,正弦,值最大,绝对值就最大.不懂得验根,增根不知舍去由|5sin(θ+ φ)− a−4|max=17得a=8（舍去）或 a = −26,a= −16（舍去）或a=18不懂得验根,真假不分由|5−a−4|=17得2个错误a值没有理解绝对值的含义点到直线的距离公 式 错 误,d =3cosθ+4sinθ−a−4√1+42 ,缺绝对值符号，或d=|3cosθ+4sinθ−a−4|√1+4等公式不熟三角变形出错3cosθ+3sinθ = √5sin(θ+φ)3cosθ +3sinθ =25sin(θ+φ)公式不熟23题分类讨论出错不理解绝对值的定义,不会去掉绝对值误用绝对值不等式不理解大于与恒大于的区别解不等式出错计算能力差,特别是二次不等式的求解不熟练解不等式后,集合运算出错没有在分类的条件下求交集,概念不清不等式符号使用错误数学符号表达混乱,书写不注意细节解题步骤不完整解题逻辑性不强,关键步骤不会表达

(二)理科卷

题 号考生的典型错误原因分析13题12粗心,忘记开方3 a,b的模用错或计算错误14题−1 3找错区域端点13没正确认识到z在目标函数中的几何意义15题3 2,2,√2,1 2.概念不清及计算错误16题126√6 32三个侧面三角形取特例:等边三角形17题a2 3 sin A=sin A sin A3 sin A ;sinB sinC=23错用正弦定理cosB cosC+sinB sinC=cos(B+C);cosB cosC−sinB sinC=cos(B+C)两角和与差的余弦公式记忆错误cos(B+C)=cosA 诱导公式记忆错误√18题第一问不会证线面垂直基础差,不会入手第一问错将AB⊥PD写为AB//PD 笔误所建系三条坐标轴不两两垂直想当然地根据图形认为两两垂直建系后点坐标错误错将底面当成正方形或是边长比为1:2的矩形最后结论正负号错误不会或忘记判断二面角的平面角是钝角19题X−B(0.0026,16),B−X(16,0.0026),X−(16,0.0026)等二项分布概念模糊EX=np(1−p)二项分布期望与方差公式混淆P(X≥1)=1−P(X≤1),P(X≥1)=P(X＜1)对立事件理解不到位s2=1 16∑16i=1(xi−)2等方差公式不熟练1−0.997416≈ 0.0418,16×0.0026=0.416,1 15(16×9.97−9.22)=10.2.计算失误20题在第(1)问,将四个点全部代入椭圆方程,求出a,b,没对P1的位置作出判断说明.审题粗心在第(1)问,将P3,P4分别代入椭圆方程,求出a,b,但没对P1的位置作出判断说明.审题粗心在第(1)问,将P2,P3,P4代入椭圆方程,求解方程组出错.运算能力差

题 号典型错误原因分析20题在第(2)问,漏写l与x轴垂直的情形 审题粗心,思维不严谨在第 (2)问,将直线 l:y =kx+n代入 x24+y2=1得整理出错运算能力差在第 (2)问,将直线 l:y =kx+n代入 x24+y2=1得到(4k2+1)x2+8kmx+4m2−4=0后计算x1+x2,x1·x2出错一元二次方程的根与系数的关系公式记忆出错在第(2)问,未能将k1+k2=y1−1 x1+y2−1 x2转化成2kx1x2+(m−1)(x1+x2)x1x2运算能力差把k1+k2= −1错写成k1·k2= −1计算粗心在第 (2)问,设直线 l:x =my+b,漏写直线l:y=t的情形思维不严谨,分类不准确21题第一问导数计算出错(1)不会复合函数的求导法则;(2)求导时混淆指数函数和幂函数;(3)计算马虎.第一问的分类错误或分类不全:(1)分a＜ 2,a=2,a＞ 2三类讨论;(2)分a＜0,a＞ 0讨论,漏了a=0;(3)f′(x)=2ae2x+(a −2)ex−1=(3a−2)ex−1分a＜2 3,a=2 3,a＞2 3讨论.第(1)种分类学生主要受到了(a−2)ex的影响;第(2)种分类主要漏了a=0,不全面;第(3)种错误是因为计算错误,学生以为可以把ex与e2x合并在一起,结果也导致了分类的错误.第一问讨论a＞0的单调性时,单调性判断错误(增减区间写反了)主要原因是解不等式时＞与＜号判断错误,或者笔误第一问利用换元法令t=ex,没有注意t＞ 0,最后没有把g(t)还原为f(x)学生有换元的意识,但容易忽略换元后必须先讨论新元t的取值范围第二问,没有找到两个点使其函数值大于0,或者没有说明limx→−∞f(x)=+∞,limx→+∞f(x)=+∞学生认为先减后增的函数,只需要保证极小值小于0,就可以保证函数有两个零点(类似于二次函数),对函数存在零点的问题本质理解不到位第二问,计算到f(−lna)=1−1 a+lna＜0后,不会解不等式,或计算不准确.学生不会利用函数的思想处理不等式的问题22,23同文科

四、对中学数学教学的几点思考

1.教学上要正确认识数学概念与数学解题的关系

数学概念是反映数学对象的本质属性的思维形式,是数学知识体系(定理,法则等)的基石,是数学思想方法的载体,也是数学研究的起点,判断、推理、计算、证明和解决问题的依据.“一个定义、几项注意、举例训练、反复练习、准备考试”,只会让学生认为学数学就是解题.重解题技巧、轻概念生成,追求习题讲解的最大化和概念学习的最小化,这是目前数学教学存在的误区.《普通高中数学课程标准》指出:“数学教学中应强调对基本概念和基本思想的理解和掌握,对一些核心的概念和基本思想要贯穿高中数学教学的始终,帮助学生逐步理解．由于数学高度抽象的特点,注意体现基本概念的来龙去脉．在教学中要引导学生经历具体实例抽象数学概念的过程,在初步运用中逐步理解概念的本质”.数学概念内涵与外延的理解需要通过解题来完成,解题之后留给学生的应是概念而不是题.“走出题海”就是需要教师善于利用有限的解题帮助学生通过数学解题达到理解概念、掌握方法.

2.高一、高二的学习与高三的应试复习要有机结合

从师生对试题的感觉来看,2017年全国高考数学卷没有一道难题、偏题,但是文、理科平均得分都不尽人意.评卷过程中我们发现令人惋惜的现象是计算能力支撑不了正确的解题思路,书写不规范导致失分或后面解答全盘皆错.这些问题的解决不是高三一年的应试复习就能解决的.高三复习超越高一、高二学习的关键在于横向优化和纵向深化,即横向综合性的加强和纵向思想性的揭示,形成从知识到方法,到能力的提高,实现数学概念理解与解题的双向沟通.这种超越没有高一、高二养成的思维习惯是难以完成的.这就要求高一、高二教学过程中教师要为学生示范计算的过程,书写的规范.数学思想的渗透,也需要从高一、高二的教学开始.否则高三各种题型解法、解题策略、专题讲座训练都是空谈.

3.重视培养数学的阅读能力

2017年全国卷试题加强了数学阅读与表达能力,学生的答卷反映出“哪里不会考哪里！”,特别是理科第19题的解答非常不理想.从笔者的经验来看,中学数学教学对数学语言的表达、数学符号书写的规范性强调较多,但对数学的阅读强调不足.

前苏联教学、教育家斯托利亚尔言:“数学教学也就是数学语言的教学”.而语言的教学是离不开阅读的.阅读数学是一个特殊的认识过程,决不是“授”、“受”之间能交割完的事.不少学生上课听得津津有味,下课做的一塌糊涂,其中的原因之一就是没能正确地“阅读”老师讲课的笔记.事实上,老师的讲课与板书、学生的作业与考试最后都是以“文字”呈现在学生的笔记、解答之中,学生只有通过阅读才能实现对数学知识的认知加工、思维消化,从而通过自身的再创造活动才能被接受,并纳入其认知结构中.

如何在教学中培养学生的阅读能力?需要广大中学教师从课堂教学到课后学习多方面结合起来进行研究.如预习是教学中的一个重要环节,也是培养学生阅读能力的一个重要途径.预习的过程中学生必须对教材进行全篇的阅读,了解所学内容的目标,重点与难点以及与旧知识间的内在联系,找出自己不懂或不足的地方,然后带着问题听课.带着学生阅读数学论文,特别是各种解题方法的小论文也是一种很好的途径.通过培养学生的数学阅读能力,养成学生优良的数学阅读习惯和方式,才能提高课堂教学效果.