2017年高考函数与导数试题分析与2018年高考备考建议

2017-10-13深圳市教育科学研究院518024李志敏

中学数学研究(广东) 2017年17期

深圳市教育科学研究院 (518024) 李志敏

深圳市教育科学研究院 (518024) 李志敏

“函数与导数”是中学数学的重点内容,依据高考重点内容重点考查的原则,在历届高考试题中“函数与导数”试题是重点考查对象,其试题往往综合性强,解法灵活多变,部分试题承载压轴使命.因此,要想在高考中取得较好的成绩,函数与导数试题不可小觑,我们有必要研究其命题规律和解题策略.

一、2017年高考I卷“函数与导数”试题分析

(一)试题展示与评析

2017年全国高考I卷理科数学“函数与导数”试题如下

1．(2017年全国高考新课标I卷理科数学第5题)函数f(x)在(−∞,+∞)单调递减,且为奇函数．若f(−1)=−1,则满足−1≤f(x−2)≤1的x的取值范围是( )

A.[−2,2] B.[−1,1] C.[0,4] D.[1,3]

评析本题主要考查函数的单调性和奇偶性等知识点,在全国高考试题中,考查函数的单调性和奇偶性是一类常考题型,题目形式常考常新,本题属基础题.

2．(2017年全国高考新课标I卷理科数学第11题)设x,y,z为正数,且2x=3y=5z,则( )

A.2x＜3y＜5z B.5z＜2x＜3y

C.3y＜5z＜2x D.3y＜2x＜5z

评析本题常见的解法是设

显然k＞1,然后,通过取对数(如取常用对数),用k分别表示2x、3y、5z,采用作差或作商比较法比较其大小,答案为D.主要考点是指数函数与对数函数的性质,指数和对数的运算,等价转换的数学思想,考查考生的运算求解能力,难度中等.

3．(2017年全国高考新课标I卷理科数学第16题)如图1,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.

图1

当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为.

评析本题主要考点是圆的性质(垂径定理),正棱锥的性质,勾股定理,棱锥的体积,以及用导数研究函数的最大值的有关知识等.基本解法是恰当引进变量建立目标函数,并求函数的最大值,是一道典型的运用函数解决几何问题的应用题.也是一道非常漂亮的函数应用题,充分体现了数学的应用价值,考查了考生的空间想象能力、数学建模能力和运算能力等.本题综合性强,难度较大,属于压轴题.依据历届高考命题规律,理科函数小题往往是2道小题,据此我们研判,命题者是将此题以立体几何题模块设置的试题.

4．(2017年全国高考新课标I卷理科数学第21题)已知函数f(x)=ae2x+(a−2)ex−x．

(1)讨论f(x)的单调性;

(2)若f(x)有两个零点,求a的取值范围．

评析本题是导数在函数上的应用题,主要考点是函数的单调性、函数的极值和函数的零点问题.与2016年全国高考新课标I卷理科数学第21题的第1问和文科第21题基本类似,其解法也基本相同,其创新之处在于确定零点存在性时,寻找使函数值为正值的点需进行巧妙的转换(不等式放缩).考生在解答本题时的主要错误是:求导错误、分类不全和考虑不周等,第2问大部分考生默认函数的图象与x轴是有交点的,忽略了函数零点的存在性的证明,即忽略了在函数图象与x轴交点两侧函数值异号的说明.本题不偏不怪,入口浅,区分度好,综合性强,属压轴题.

2017年全国高考I卷文科数学“函数与导数”试题如下

评析本题是函数图象的识图问题,需考生在研究函数的性质的基础上,判别函数图象的形状,这类问题在全国高考试题中屡屡出现.实际上,这类问题主要考点是函数的单调性、奇偶性、函数的定义域和值域等知识,考查考生综合运用函数知识分析问题和解决问题的能力.本题属中等难度试题.

2．(2017年全国高考新课标I卷文科数学第9题)已知函数f(x)=lnx+ln(2−x),则

A.f(x)在(0,2)单调递增

B.f(x)在(0,2)单调递减

C.y=f(x)的图像关于直线x=1对称

D.y=f(x)的图像关于点(1,0)对称

评析本题考查考生综合运用函数知识来分析问题和解决问题的能力,主要考点是函数的单调性、对称性.函数的对称性是高考中一类较难的问题,其题型不断创新.在高考复习过程中,不可忽视函数图象对称性问题的复习和研究(函数图象的轴对称和中心对称问题).

3．(2017年全国高考新课标I卷文科数学第14题)曲线在点(1,2)处的切线方程为.

评析函数图象的切线问题是高考的高频考点,考生在解题时,要分清试题是“已知切点”问题还是“未知切点”问题,“未知切点”一般需设切点坐标,在平时的教学中要加强训练.

4．(2017年全国高考新课标I卷文科数学第21题)已知函数f(x)=ex(ex−a)−a2x.

(1)讨论f(x)的单调性;

(2)若f(x)≥0,求a的取值范围.

评析本题是导数研究函数的综合性试题,主要考点是函数的单调性和极值.第(2)问实际上是将不等式恒成立问题转化为求函数的最小值问题.考查分类讨论思想、等价转换思想和数形结合思想,本题难度并不是很大,属中等偏上难度试题.考生的主要问题是:运算不过关,分类不全面.

(二)试题分析

1.题型分值稳定,形式略有创新

2017年全国I卷高考数学试题中的“函数与导数”模块试题,继承多年来新课程高考命题风格,稳定与创新并存,题型与分值基本稳定,但综合性有所增加,注重从知识的交汇处命题,如2017年全国高考I卷理科数学第16题是代数与几何结合的综合题.从对历届高考全国I卷理科数学试题分析可知,通常理科数学只有2道函数小题,而立体几何也有2道小题,若将2017年全国高考I卷理科数学第16题定位为函数试题,则2017年理科数学相比前几年的“函数与导数”模块就多了1道小题,立体几何就少了1道小题,故我们认为,2017年全国高考I卷理科数学第16题应定位为立体几何小题.2017年文科数学也有一点变化,文科数学的第8题,若算“函数与导数”模块试题,则“三角函数与解三角形”模块就少了1道小题,综合多年全国I卷高考数学试题命题情况,我们认为:全国I卷高考数学试题中的“函数与导数”模块,一般来说,理科为2道小题和1道大题,总分值为22分;文科为3道小题和1道大题,总分值为27分.

下面是近三年全国新课标I卷导数与函数试题的分值、题型和考查知识点分布情况:

表一:近三年新课标I卷理科“函数与导数”试题考点与分值统计表

表二:近三年新课标I卷文科“函数与导数”试题考点与分值统计表

从以上两表不难看出,全国高考数学试题中的“函数与导数”模块试题总体稳定,小题主要考查函数的单调性、奇偶性和对称性问题,其中函数图象的识别是常考的一种题型,数形结合思想也常有涉及,指数和对数函数的性质及其运算有加强的趋势;解答题主要考查导数在研究函数中的应用,主要题型有函数的零点问题、不等式证明问题,不等式恒成立问题等.

2.凸显能力立意,承载压轴使命

2017年全国I卷在函数与导数试题的设计上,充分体现基础性、综合性、应用性和创新性,文理数学试题均有1道比较基础的小题,1道压轴小题,文科还多了1道中等难度小题,文理各有1道压轴的解答题.试题不偏不怪,入口浅,寓意深,层次分明,区分度好,解法灵活,较好地考查了不同层次学生的分析问题和解决问题的能力.文科第8题和第9题,深刻地考查了考生的直观想象能力和逻辑推理能力,第21题考查了考生运算求解和逻辑推理能力,理科第16题考查了考生的数学建模能力和运算求解能力等.对服务高校选拔,导向教学起着非常重要的把关作用.

3.考查数学素养,渗透思想方法

试题注重数学思想方法的考查,2017年全国高考I卷理科数学第16题,考查了函数与导数在立体几何中的应用,考查了考生数学建模、直观想象、数学运算等数学核心素养,考查了函数方程和等价转换等数学思想方法,文理科第21题,考查了数形结合思想、分类讨论思想和等价转换思想,试题灵活,解法多样,注意对考生思维灵活性的考查,注重考查考生的数学素养.

二、近年全国高考I卷数学“函数与导数”试题热点题型分析

纵观近几年全国高考I卷数学试题,在“函数与导数”试题的设计上,有下列一些热点题型:

1.有关“函数的图象和性质”试题

有关函数的图象和性质试题是高考热点问题,其命题形式主要有下列两种:

(1)根据函数的解析式确定函数的单调性、奇偶性、对称性,判别函数的图象形状等

如,2017年全国高考I卷文科数学第8题,2012年全国高考I卷理科数学第10题,2013年全国高考I卷文科数学第9题,2014年全国高考I卷理科数学第6题,2015年全国高考I卷理科第13题,2016年全国高考I卷文科第9题等.均是研究函数的性质的试题.

例1 (2017年全国高考新课标I卷文科数学第9题)题目见上文文科第2题.

评析本题是根据函数解析式研究函数的图象和性质.

例2(2016年全国高考I卷理科数学第7题)

(1)函数y=2x2−e|x|在[−2,2]的图象大致为

评析本题是根据函数解析式研究函数的图象形状.有时需要考生根据条件建立函数解析式,再来判断函数的图象或研究函数的其它性质等.如:

例3 (2014年全国高考新课标I卷理科数学第6题)如图2,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P作直线OA的垂线,垂足为M,将点M 到直线OP的距离表示为x的函数f(x),则y=f(x)在[0,π]上的图象大致为

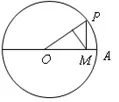
图2

评析本题需要考生根据条件建立函数解析式,这是函数试题中的一类重要题型,较深刻地考查了考生的数学抽象和数学建模能力.类似地,2017年全国高考I卷理科数学第16题也属于此类问题,只不过该题不是图象识别,而是求所列出的函数的最大值.

例3 (2017年全国高考新课标I卷理科数学第16题)题目见上文理科第3题.

简解如图3,依题意,连接OD,交BC 与点 G,则 OD⊥BC,

图3

评析本题以立体几何为背景,涉及平面几何和立体几何诸多知识,通过建立目标函数,将几何问题转化为代数问题,考查考生数学建模、直观想象、数学运算等数学核心素养.

(2)根据函数的性质,如根据函数的单调性、奇偶性和对称性,求函数解析式中的参数

例4 (2013年全国高考I卷理科数学第16题)若函数f(x)=(1−x2)(x2+ax+b)的图象关于直线x=−2对称,则f(x)的最大值是.

评析本题是根据函数的对称性求函数解析式中的参数,进而求函数的最大值.

评析本题是根据函数的奇偶性求函数解析式中的参数.

例6 (2015年全国新课标I卷文科第12题)设函数y=f(x)的图像与y=2x+a的图像关于直线y+−x对称,且 f(−2)+f(−4)=1,则 a=

A.−1 B.1 C.2 D.4

评析本题是根据函数对称性求函数解析式中的参数.

例7 (2016年全国新课标I卷文科第12题)若函数f(x)=sin2x+asinx在(−∞,+∞)单调递增,则a的取值范围是

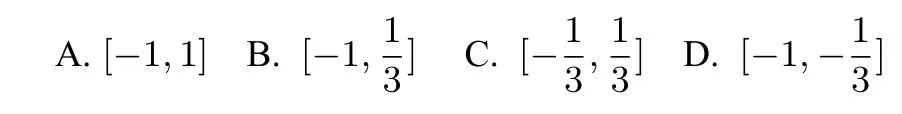
评析本题是根据函数的单调性求函数解析式中的参数.

2.运用导数研究函数的性质

导数是研究函数的工具,通过导数研究函数图象的切线,函数的单调性、极值、最值和函数的零点等,其中有关函数零点的试题出现的频率较大,是高考热点问题.

例8 (2015年全国新课标I卷文科第14题)已知函数f(x)=ax3+x+1的图像在点(1,f(1))的处的切线过点(2,7),则a=.

例10 (2013年全国高考I卷文科数学第20题)已知函数f(x)=ex(ax+b)−x2−4x,曲线y=f(x)在点(0,f(0))处切线方程为y=4x+4.

(I)求a,b的值;

(II)讨论f(x)的单调性,并求f(x)的极大值.例11(2014年全国高考I卷,理科数学第11题,文科数学第12题)已知函数f(x)=ax3−3x2+1,若f(x)存在唯一的零点x0,且x0＞0,则a的取值范围是

A.(2,+∞) B.(1,+∞) C.(−∞,−2) D.(−∞,−1)例12 (2015年全国高考I卷理科数学第21题)已知函数

(I)当a为何值时,x轴为曲线y=f(x)的切线;

(II)用min{m,n}表示m,n中的最小值,设函数h(x)=min{f(x),g(x)},讨论h(x)零点的个数.

例13(2016年全国高考I卷理科数学第21题)已知函数f(x)=(x−2)ex+a(x−1)2有两个零点.

(I)求a的取值范围;

(II)设x1,x2是f(x)的两个零点,证明:x1+x2＜2.

例14 (2016年全国高考I卷文科数学第21题)已知函数f(x)=(x−2)ex+a(x−1)2.

(I)讨论f(x)的单调性;

(II)若f(x)有两个零点,求a的取值范围.

例15(2015年全国高考I卷文科数学第21题)设函数f(x)=e2x+alnx.

(I)讨论f(x)的导函数f′(x)的零点的个数;

用导数研究函数问题时,应注意如下两个常见的解题技巧:

(1)画出函数图象的草图

导数是研究函数性态的工具,在解题时,要注意在研究“函数的定义域、单调性、奇偶性、函数图象与坐标轴的交点、函数图象的极值点、拐点、函数值的正负情况”的基础上,画出函数图象的草图,为了方便研究函数的单调性,常常还需画出导函数图象的草图或示意图,通过数形结合的思想方法来分析解决问题.

例16 (2016年全国I卷文科数学第21题)已知函数f(x)=(x−2)ex+a(x−1)2.

(I)讨论f(x)的单调性;

(II)若f(x)有两个零点,求a的取值范围.

分析本题也是2016年全国I卷理科的第1问,可考虑先求出函数的导数

求导后,尽可能将导数化成积或商的形式,便于判断导数值的符号.在分析问题时,可画出反映导函数值的正负的函数图象的示意图(可选择能决定导数值正负的函数,不是严格意义的函数的图象,而是反映其符号的示意图),表示出其单调性和轴的交点即可.如当a＜0时,令f′(x)=(x − 1)(ex+2a)=0,可得 x=ln(−2a)和 x=1,据此画出反映导函数值正负的示意图:

根据导函数值的示意图,可将问题分为三类:①当ln(−2a)＞ 1,即a＞时;②当ln(−2a)＜1,即a＜时;③当ln(−2a)=1,即a=时.这种通过画草图的方法,使分类合理自然,化难为易.类似地,第(II)问也可结合图象进行分析求解.

例17(2015年高考全国卷I理科数学第12题)设函数f(x)=ex(2x−1)−ax+a,其中a＜1,若存在唯一的整数x0,使得f(x0)＜0,则a的取值范围是( )

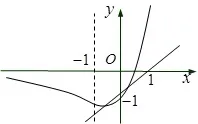
图4

解析问题可转化为存在唯一的整数x0,不等式ex(2x−1)＜a(x−1)成立的问题.设g(x)=ex(2x−1),h(x)=a(x−1).如图4,现在画出函数g(x)=ex(2x−1)和h(x)=a(x−1)的图象,运用数形结合的方法来解决问题.因为g′(x)=ex(2x+1),所以,当时,g′(x)＜ 0,当时,g′(x) ＞ 0,所以,函数g(x)在上单调递减,在单调递增,当时,,因为g(0)= −1,g(1)=3e＞ 0,直线h(x)=a(x−1)恒过(1,0)且斜率为a,由题设可知存在唯一的整数x0,使得g(x)＜h(x),结合图象分析可得g(0)＜ h(0)且g(−1)≥ h(−1),即−a＞−1且−3e−1≥ −a−a,解得＜1,故选D.

(2)导数零点的“设而不求”

在利用导数研究函数时,当导函数的零点存在且不易求出时,可采用导函数零点的“设而不求”技巧来研究问题.在解决问题时,要注意正确运用函数零点存在性定理.

例18 (2013年全国II卷理科数学第2题)已知函数f(x)=ex−ln(x+m)．

(I)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;

(II)当m ≤ 2时,证明f(x)＞ 0．

解析 (I)略.

评析本题中的第(II)问,导数f′(x)=的零点是存在的,但不易求出,可设导函数的零点为x0,设而不求,并注意到零点满足方程f′(x0)=0,通过适当的代换,问题便迎刃而解.

3.运用导数研究不等式问题

在高考试题中,常常出现“不等式证明问题”、“不等式恒成立问题”和“不等式有解问题”等等,这些问题有时可通过等价转换将问题转化为函数问题,进而用导数去研究函数.解决这类问题的关键是合理转化和恰当构造新函数.

例19(2013年全国高考I卷理科数学第21题)已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.

(1)求a,b,c,d的值;

(2)若x≥−2时,f(x)≤kg(x),求k的取值范围.

评析本题通过构造函数F(x)=kg(x)−f(x),把不等式f(x)≤kg(x)(x≥−2)恒成立问题转化为求函数F(x)的最小值问题.

例20(2016年全国高考卷I卷理科数学第21题)已知函数f(x)=(x−2)ex+a(x−1)2有两个零点.

(I)求a的取值范围;

(II)设x1,x2是f(x)的两个零点,证明:x1+x2＜2.

评析本题中第(II)问是一个不等式问题,通过合理转化,构造新函数,最终转化为求函数的最大值问题.

例21(2014年高考全国I卷第21题)设函数f(x)=,曲线y=f(x)在点(1,f(1))处的切线为y=e(x−1)+2.

(I)求a,b;

(II)证明:f(x)＞ 1．

评析将不等式问题转化为函数问题,需合理转化,本题中,若直接求函数的最小值,即证明f(x)min＞1很难达到目的,若进行适当变换,转化为证明不等式xlnx＞成立,并构造函数g(x)=xlnx和h(x)分别研究这两个函数,结果发现g(x)min≥h(x)max(最大值与最小值在不同处取得),问题便得到解决.

三、2018年高考数学备考建议

1.研究高考,把握高考命题方向

研究考纲,研究高考试题,把握全国高考命题方向,正确把握复习的重点和难度,不做无用功.高三教师要做一定量的高考题,建议认真研究2007年以来的全国(I)(II)(III)卷试题,体会高考试题的味道,了解高考命题方向.

2.因材施教,实施分层推进策略

根据本校本班学生的实际情况,实施有效教学,分类要求,分层推进.重点学校和重点班的学生,在夯实基础的前提下,可考虑挑战压轴题,争取拿高分,对数学“尖子生”可研究特殊的培优方式,使“尖子生”充分发挥其学科优势;对基础薄弱的学生的复习要重视基础,可考虑放弃一些讲了也不容易明白的较难问题.教学难度既要符合考纲,又要符合学生的实际,教学容量和难度要适中.