2017年高考全国卷I理科数学第20题结论的推广及其简证—该题的结论是《高考数学真题解密》定理6-22的特例

北京丰台二中(100071) 甘志国

2017年高考全国卷I理科数学第20题结论的推广及其简证—该题的结论是《高考数学真题解密》定理6-22的特例

北京丰台二中(100071) 甘志国

高考题 (2017年高考全国卷I理科数学第20题)已知椭圆,四点P1(1,1),P2(0,1),中恰有三点在椭圆C上.

(1)求C的方程;

(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为−1,证明:l过定点.

解 (1)若椭圆C过点P2(0,1),可得b=1,进而可得椭圆C不过点P1(1,1),所以椭圆C过三点

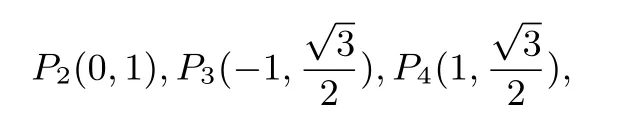
而椭圆C不可能同时过点P1(1,1),P4.综上所述,可得椭圆C的方程是

(2)可设直线PA:y=kx+1,进而可得

(2)的另证 当直线l的斜率存在时,可设直线l:y=kx+m.由

由直线l:y=kx+m不经过点P2(0,1),可得m1,所以m=−2k−1,得直线l:y=k(x−2)−1,所以直线l过定点,且该定点的坐标是(2,−1).

当直线l的斜率不存在时,由题设可求得直线l的方程是x=2,它也过点(2,−1).

综上所述,可得直线l过定点,且该定点的坐标是(2,−1).

(2)的再证 把原题中的所有图形全部向下平移1个单位,原图形中的点P2,A,B平移后分别变为O′(0,0),A′,B′,直线l,x轴,y轴平移后分别变为直线l′,x′轴,y′轴.椭圆C:平移后变为椭圆即椭圆 C′:x′2+4y′2+8y′=0.因为直线 l′不过点 O′(0,0),所以可设直线 l′:mx′+ny′=1.进而可得,由直线 O′A,O′B组成的曲线方程为

即该曲线表示过原点O′的两条直线.又因为不共线的三点O′,A′,B′在该曲线上,所以它就是表示由直线 O′A′,O′B′组成的曲线方程．

因为直线O′A′,O′B′的斜率均存在且不相等,所以以下关于的方程有两个不相等的实根即k1,k2(得8n+40):

的解(x′,y′)=(2,−2),进而可得直线l过定点,且该定点的坐标是(2,−1).解毕.

接下来就是研究这道高考题第(2)问的一般情形.

拙文[1]及拙著[2]由“(2)的另证”的方法,拙著[3]由“(2)的再证”的方法均给出了其一般情形及其证明.

下面介绍拙著[3]的相应结论及其证明.

定理 (即拙著[3]的定理6-22)设P(x0,y0)是定二次曲线

上的一个定点,PA,PB是该曲线的两条动弦,其所在直线的斜率均存在(分别设为k1,k2),直线AB不过点P,则

②k1k2为定值直线AB过定点

(2)①当b=0时,k1+k2为定值λ⇔直线AB的方向向量为(2by0+d,2(ax0+λby0)+(c+λd))．

证明 因为把直线平移后这条直线的方向向量不变(因而其斜率也不变),所以只需证明把定理中对应的所有图形沿向量(O是坐标原点)平移后的结论成立.

设OA,OB是定二次曲线

Γ:a(x+x0)2+b(y+y0)2+c(x+x0)+d(y+y0)+e=0,(|a|+|b|0),即

(1)①k1k2⇔ 直线AB 的方向向量为(bc′,−ad′)．

②k1k2为定值⇔直线AB过定点

(2)①当b=0时,k1+k2为定值λ⇔直线AB的方向向量为 (d′,c′+ λd′)．

证明如下.

因为直线AB不过原点O,所以可设

AB:mx+ny=1.

于是,由直线OA,OB组成的曲线方程为

因为该曲线上有三点O,A,B,又因为该式左边是x,y的二次齐次式,所以它可在ℝ上因式分解为

即该曲线表示过原点的两条直线.又因为不共线的三点O,A,B在该曲线上,所以它就是表示由直线OA,OB组成的曲线方程．

理由:因为直线OA,OB的斜率均存在且不相等,所以以下关于的方程有两个不相等的实根即k1,k2(得b+d′n0),

所以

由此可得,欲证结论成立．

推论1 设P(x0,y0)是定抛物线y2=2px(p＞0)上的一个定点,PA,PB是该抛物线的两条弦,其所在直线的斜率分别为k1,k2．

(1)k1k2为定值λ(显然λ0)⇔直线AB过定点

(2)k1+k2=λ(λ为定值且不为0)⇔直线AB过定点k1+k2=0⇔直线AB的方向向量为(−y0,p)．

推论2 设P(x0,y0)是定曲线λx2+µy2=1(λµ0)上的一个定点,PA,PB是该曲线的两条弦,其所在直线的斜率分别为k1,k2．

(1)k1k2= δ(δ为定值且不为)⇔直线AB过定点⇔直线AB的方向向量为 (−x0,y0)．

(2)k1+k2=δ(δ为定值且不为0)⇔直线AB过定点);k1+k2=0⇔直线AB的方向向量为 (µy0,λx0)．

由定理及隐函数的导数,还可证得

推论3 设P(x0,y0)是定二次曲线

上的一个定点,PA,PB是该曲线的两条动弦,其所在直线的斜率均存在(分别设为k1,k2),则

(2)若k1+k2=0,则直线AB与曲线Γ的过定点P的切线的斜率互为相反数或均不存在．

[1]甘志国.圆锥曲线的一条美丽性质[J].学数学,2014(1-3):43-47,24.

[2]甘志国著.高考压轴题(下)[M].哈尔滨:哈尔滨工业大学出版社,2014,153-161.

[3]甘志国著.数学高考真题解密[M].北京:清华大学出版社,2015,100-102