基于功率谱对消的时域相关认知跳频谱检测算法
2017-10-12李彤苗成林吕军
李彤, 苗成林, 吕军
(装甲兵工程学院 信息工程系, 北京 100072)
基于功率谱对消的时域相关认知跳频谱检测算法
李彤, 苗成林, 吕军
(装甲兵工程学院 信息工程系, 北京 100072)
认知跳频技术将认知无线电运用到跳频通信中,通过检测认知跳频频谱中的“频谱空穴”来更新跳频点集,避免频点碰撞,提高频谱利用率。针对频谱检测中的时域相关算法因噪声和授权信号的存在,导致频谱空穴的判定门限难以确定,从而使占用信号的检测概率较低的问题,提出了一种基于功率谱对消的时域相关算法来检测跳频谱。与未经过功率谱对消运算的传统时域相关算法相比,该算法能有效提高信号的检测概率,具有实时性好、克服白噪声不确定性、抑制授权信号干扰的优点。理论分析与仿真结果表明,基于功率谱对消的时域相关算法优于传统时域相关算法。
通信技术; 认知跳频; 功率谱对消; 时域相关
Abstract: Cognitive frequency hopping technology is to apply cognitive radio to frequency hopping communication. The spectrum hole in cognitive frequency hopping spectrum can be detected effectively to avoid the collision of frequency points and improve the spectral efficiency to update the frequency hopping points. The time-domain correlation algorithm in spectrum detection technology for cognitive radio has some defects in anti-interference, universality and real-time performance due to the existence of noise and primary signals. A time-domain correlation algorithm based on power spectrum cancellation is proposed to detect the cognitive frequency hopping spectrum. The proposed algorithm can be used to improve the detection probability of signals. Moreover, it can overcome the noise uncertainty and restrain the primary signals. Theoretical analysis and computer simulation demonstrate that the time-domain correlation algorithm based on power spectrum cancellation is superior to traditional time-domain correlation algorithm.
Key words: communication technology; cognitive frequency hopping; power spectrum cancellation; time-domain correlation
0 引言
跳频通信具有低截获、抗干扰等特点,在军事通信、网电空间战中广泛应用,当前战术通信电台多采用跳频技术来提高通信的抗干扰能力。然而传统跳频通信是在确定、静态的频点集上进行通信,尽管使用多套(约定的备用方案)跳频点集,但由于缺少对频谱的认知能力,使跳频点集固定,不能高效地利用频谱资源;同时,由于军事电磁对抗以及局部区域内众多的无线网络,跳频点碰撞概率增高,使通信误码率增加,造成通信质量下降。针对以上问题,认知跳频(CHF)技术被提出来[1]。CHF系统结构如图1所示。
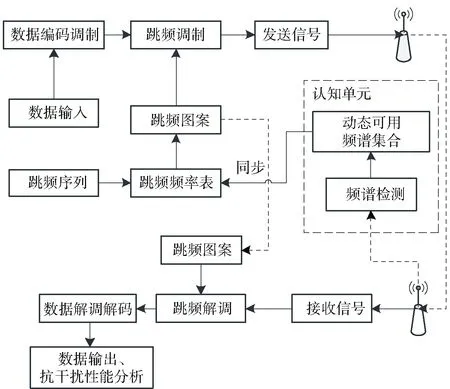
图1 CHF系统结构Fig.1 Cognitive frequency hopping system
图1所示的CHF系统与传统跳频相比,增加了认知单元。认知单元是CHF系统的核心部件,可在接收端获取并处理信道中的频谱信号,发现频谱空穴,更新可用频点集,从而降低频点碰撞概率,减小瞄准式干扰。军用电台跳频速率较快,CHF系统要求频谱检测的时间小于跳频序列周期,以确保进入下一周期时能及时更新跳频点集,因此需要实时性较高的频谱检测技术。
现有的认知无线电频谱检测技术可以分为两类:协作式频谱检测技术[2]和基于谱的检测技术[3-7]。协作式频谱检测技术需要多节点将各自的感知信息汇总到融合中心进行综合处理,该方法需要额外的通信开销,对收发端独立的CHF系统并不适用[2]。基于谱的频谱检测方法包括匹配滤波[3]、能量检测[4]、延迟相乘检测[5]、循环检测[6]和时域相关检测[7]等。其中:匹配滤波器检测方法需要发射端的先验信息,同步要求高[3];能量检测方法无需先验信息,但是受到噪声的影响严重[4];延迟相乘检测方法只针对特定的信号,需要获得发射端滤波参数,普适性差[5];循环检测方法计算复杂度高,实时性较差[6];时域相关检测方法无需先验知识,实时性好[7],但判决门限对噪声的期望和方差敏感,当存在其他频带内信号时,判决规则失效。鉴于以上方法的不足,本文对时域相关算法进行研究,以解决在CHF系统中授权用户的干扰问题,并克服噪声的不确定性。
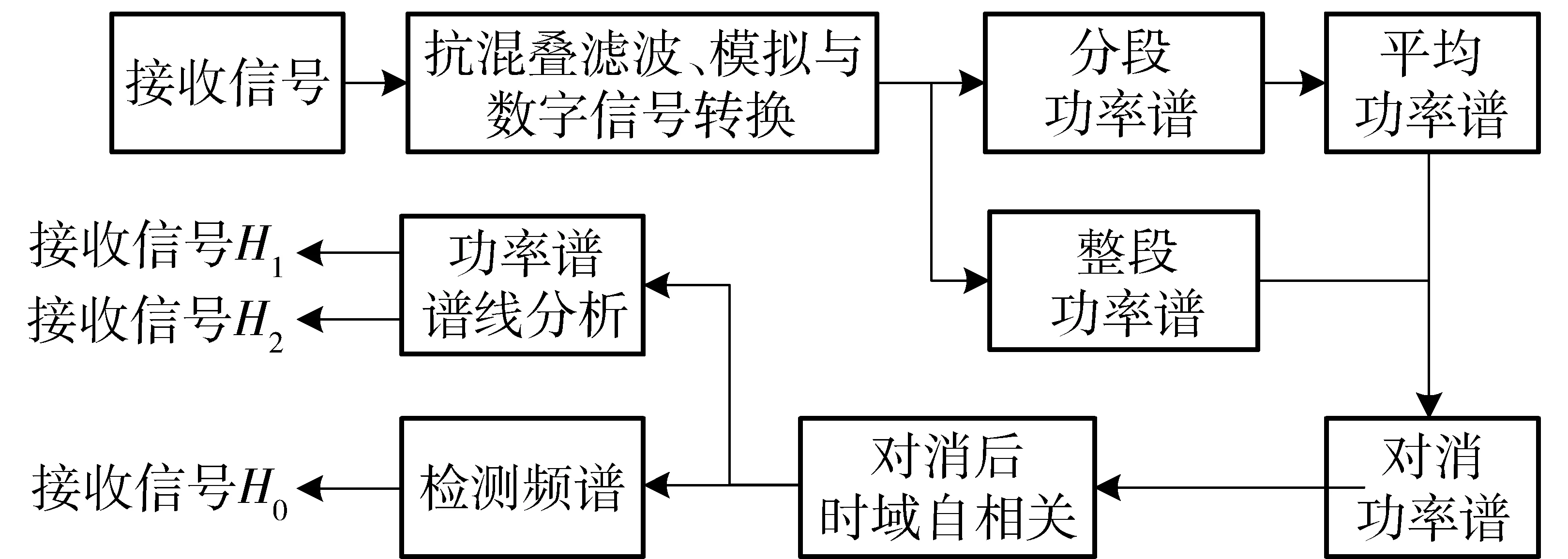
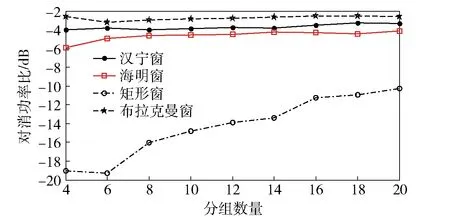
传统时域相关算法一般通过对信号自相关函数的幅度采样,将采样值累加运算得到统计量,依据该统计量的最大似然或者最小二乘法判决结果来判断频段内是否有跳频信号[7]。时域相关算法流程如图2所示。在观测时间0<τ 图2 时域相关运算流程图Fig.2 Time-domain correlation processing 在利用功率谱对消的方法中,文献[8]提出了功率谱对消的跳频信号检测算法,将功率谱对消的方法应用在跳频信号的检测中,通过对消运算来减小定频信号对跳频信号检测的影响。文献[9]提出对功率谱对消后的信号采用短时傅里叶变换来进行时频分析的算法,以有效提高跳频信号的检测概率。文献[10-11]提出分段对消频谱感知算法,将功率谱对消的方法应用到认知无线电的频谱感知上,以频带内一些谱线强度和与剩余谱线强度和的比值作为检验统计量,表明功率谱对消运算能克服噪声的不确定性,证明了在认知无线电系统中的可行性。文献[12] 提出基于功率谱密度中段平均算法,以接收信号功率谱最大值与最小值之差作为检测统计量,与分段对消的思想类似,应用于认知无线电中,具有很好的检测性能。 本文延续功率谱对消的思想,针对CHF系统,使用功率谱对消的方法对传统时域相关算法进行改进,在传统时域相关算法的基础上,提出了一种基于功率谱对消的时域相关(TCPC)CHF谱检测算法(简称TCPC算法),利用功率谱分段对消运算抵消跳频频段内其他长时信号的干扰,提出检测门限的确定方法,能够计算频谱空穴的概率,判断淹没在干扰信号中的跳频信号频点,以克服噪声不确定性、区分和抑制授权信号,提高检测概率。 自组织应急网络加入到现有的通信网络中所构成的通信环境如图3所示,包括授权信号、背景噪声、网内的跳频信号和网间干扰。其中邻近网络采用跳速较快的跳频传输,授权信号(PU)采用跳速较慢的跳频或定频传输,应急网络和邻近网络中的用户都是认知用户,基站是授权用户,基站发送的信号是授权信号,对频谱的使用优先级顺序为授权信号>邻近网络>应急网络。应急网络需要感知授权用户、邻近网络和背景噪声信号,当发现授权用户或者邻近网络信号占据频点时,及时调整跳频配置,更新跳频点集。该通信环境属于典型的CHF系统。 图3 通信环境模拟图Fig.3 Simulated communication environment CHF系统的邻近网络接收机接收到的信号x(t)模型表示为 (1)式中:H0表示接收的信号只有噪声n(t);H1表示接收的信号含有跳频信号SH(t)和噪声n(t);H2表示接收的信号含有跳频信号SH(t)、背景噪声n(t)和授权信号SF(t). 噪声类型是加性高斯白噪声。 接受到的信号x(t)经过抗混叠滤波器和模拟与数字信号转换器转换为数字序列x(m),共有N个数据,x(m)的功率谱为S(k). 把x(m)分成连续的L段数据,每段数据量为M,对第t数据xt(m)求快速傅里叶变换运算,xt(m)的功率谱St(k)为 (2) 式中:a、b分别为xt(m)中含有的授权信号和跳频信号的数量;ω为xt(m)与Xt(k)傅里叶变换之间的相位关系。 对每段数据的功率谱,在时间上求平均功率谱SA(k)为 (3) 式中:xl(n)为第l段数据,计算对消功率谱为 SS(k)=S(k)-SA(k). (4) 在观测时间内,PU长时间占据频带,而跳频信号在跳频图案中跳变,假设每段数据平均含有的跳频数为g,整段数据中跳频数为h,则(3)式求平均功率谱时,跳频信号的功率谱强度会变成原来的g/h,而PU的功率谱幅度基本不变。由此可知,通过(4)式运算可以抵消大部分PU功率、将跳频信号保留下来,从而可以通过保留的信号对CHF的存在性进行检测。 由维纳- 辛钦定理可得,自相关函数与功率谱函数是一对傅里叶变换[13],从而可得 (5) 对x(t)求其自相关函数Rx(τ),其中τ为时延,0<τ (6) 式中:RHH(τ)表示跳频信号的自相关;RNN(τ)表示噪声的自相关;RNH(τ)和RHN(τ)分别表示跳频信号和噪声的互相关;RNF(τ)和RFN(τ)分别表示PU和噪声的互相关;RFF(τ)表示PU的自相关;RHF(τ)和RFH(τ)分别表示跳频信号和PU信号的互相关。 由文献[7]可知,信噪比小于1时,信号乘噪声分量可忽略不计,因此RHN(τ)和RFN(τ)与信噪比有关,当信噪比小于1 dB时,RHN(τ)≈0,RFN(τ)≈0.RHH(τ)与跳频一跳驻留时间TH有关: (7) 综上所述,对Rx(τ)可变换为: 当0<τ (8) 当TH<τ (9) 取自相关函数两端时间的平均值做特征值E1和E2: (10) 将E1和E2的归一化比值ρ作为检测统计量,来判断接受端的信号情况。 若接收端信号为H0假设,检测统计量ρ0的数学表示式如下: (11) 由(11)式可知,ρ0只与噪声的自相关RNN(τ)有关。 若接收端信号为H1假设,检测统计量ρ1的表达式为 ρ1=ρ|H1≅ (12) 若接收端信号为H2假设,检测统计量ρ2的表达式为 (13) H1与H2比较,存在跳频信号,即频谱空穴被占据时,由于RFF(τ)分量的存在,在一跳时间TH内具有很强的自相关性,使ρ1有显著的增量。但由于PU的存在,不管是否在TH内,特征比值都会有明显增量,不能再用ρ1作为是否存在频谱空穴的检测统计量。使用(5)式中功率谱对消后的R′x(τ)作为(11)式中的Rx(τ),得到最终的判决统计量为 (14) 比较对消后功率谱和x(t)的功率谱,通过谱线强度的变化来判断授权信号对某频点的占用性,对H1、H2假设进行区分,该过程对频谱空穴的检测概率没有影响。 综合以上过程,TCPC算法流程图如图4所示。 图4 TCPC算法流程图Fig.4 Flow chart of TCPC algorithm (15) 式中:erf(x)是误差函数,其表达式为 (16) 根据Neyman-Pearson准则[13]可得到门限 (17) 式中:erf-1(x)是误差函数的反函数。从(17)式可以看出,门限λ与ρ0的期望、方差和Pf有关。由于ρ0的表达式是一个确定的比值关系,该比值难以寻找确定的数学表达式,且由RNN(τ)的波形估计出该比值为恒定值,计算白噪声的期望和方差对统计量ρ0的期望、方差影响的关系如图5所示。选取观测时间τ是跳频驻留时间TH的5倍,通过1 000次蒙特卡洛实验确定噪声方差和期望,ρ0的大小限制在±0.1范围内变换。从而可知门限λ对噪声的期望和方差不敏感,可以克服噪声不确定性。 图5 噪声影响ρ0统计量示意图Fig.5 Influence of noise on ρ0 在CHF系统中,检测概率Pd是指频谱中检测到信号的概率,即频谱空穴的概率。Pd的数学表达式为Pd=P(ρ′>λ|(H1&H2)). 对消后的功率谱傅里叶变换进行采样,将大量的随机采样值代入(14)式中计算均值得到ρ′,经过M次蒙特卡洛实验,统计ρ′>λ的数量为N,从而得到检测概率Pd=N/M(100%). 仿真参数设置如下:总数据点数20 000点,CHF的频率集为2 000 Hz、3 000 Hz、4 000 Hz、5 000 Hz、6 000 Hz、8 000 Hz. 由于PU的存在,接收的授权信号频点为1 000 Hz和7 000 Hz,(11)式~(13)式中的特征值ρ0、ρ1、ρ2存在明显增量。存在授权信号时的自相关系数如图6所示,不存在授权信号时的自相关系数如图7所示。由图6可知,由于授权信号的影响,自相关函数在非原点处存在明显增量,由此可以看出传统时域相关算法失效。 图6 存在授权信号时的自相关系数示意图Fig.6 Autocorrelation coefficient with PU 图7 不存在授权信号时的自相关系数Fig.7 Autocorrelation coefficient without PU 图8 无频点碰撞的对消功率谱Fig.8 Power spectrum cancellation without collision of frequency points 使用窗函数截取数据段,计算分段功率谱,进而求得平均功率谱,再代入(4)式中计算对消功率谱。PU可能与跳频信号发生频点碰撞。PU与跳频信号不存在频点碰撞时的对消功率谱如图8所示,PU为1 000 Hz、7 000 Hz的信号;PU与跳频信号存在频点碰撞时的对消功率谱如图9所示,PU为2 000 Hz、6 000 Hz的信号。由于加窗函数截断信号造成的频谱泄露以及噪声本身的随机性使对消功率谱在碰撞频点位置有残留能量,通过设置判决门限对频点进行识别,判定规则为将某一频点处低于判定门限的频点位置判定为频谱空穴。但确定判决门限十分困难,常用的寻找极值点确定门限方法[13]无法准确地寻找到所有频点位置,因此将对消功率谱转变为自相关函数并在时域上进行检测概率的计算,从而得到频点位置信息的估计。 图9 有频点碰撞的对消功率谱Fig.9 Power spectrum cancellation with collision of frequency points 由维纳- 辛钦定理知,自相关函数与功率谱是一对傅里叶变换[13],将对消功率谱代入(5)式中得到R′x(τ),图10所示为对消后的自相关系数,可见不管有无频率碰撞,只有在时延为0附近存在大于0.5的归一化系数,可以进行频谱空穴的概率计算。 图10 对消后的自相关系数Fig.10 Autocorrelation coefficient after cancellation 图11 窗函数影响对消运算示意图Fig.11 Influence of window function on cancellation 信噪比为5 dB,窗函数分别选择汉宁窗、海明窗、矩形窗和布拉克曼窗,经过1 000次蒙特卡洛计算,得到分组数量与功率谱对消比的关系如图12所示。由图12可见,TCPC算法中平均功率谱的计算与分组数量关系不大,而选择矩形窗时,分组数目越多、对消运算的性能越好,这是因为使用矩形窗截断数据时频谱能量泄露明显,而其他3个窗对旁瓣能量都有一定的抑制。 图12 分组数量影响对消运算示意图Fig.12 Influence of number of groups on cancellation 综合图11和图12可以看出,选择布拉克曼窗的功率对消性能优于汉宁窗,汉宁窗优于海明窗,矩形窗的性能最差。 在使用分段数目为10,窗函数选择布拉克曼窗,直接数字合成方法产生总数据点数20 000点,调制方式为二进制相移键控,虚警概率分别选取0.05、0.10、0.30的条件下,对TCPC算法与传统时域相关算法(未经过对消运算的自相关检测算法)进行比较,结果如图13所示。由图13可见,在同样的虚警概率下,特别是在较低信噪比条件下,TCPC算法具有更高的检测概率,基于功率谱对消的时域相关算法优于传统的时域相关算法。 图13 时域相关算法比较示意图Fig.13 Comparison of TCPC algorithm and tranditional time-domain correlation algorithm 本文提出了一种基于功率谱对消的时域相关算法来检测CHF谱,克服了传统时域相关算法中对噪声敏感、受授权信号干扰较大的缺点,分析了分段数、窗函数类型、接收信噪比3个因素对该算法的影响,在同样的虚警概率下,基于功率谱对消的时域相关算法比传统的时域相关算法具有更高的检测概率。表明基于功率谱对消的时域相关算法能广泛应用于CHF系统的频谱检测中,为应急网络接入现有通信环境提供了一种解决方案。 References) [1] 仇帅, 陈西宏, 王澈. 认知无线电在跳频通信中的应用研究[J]. 现代防御技术, 2013, 41(5):64-69. QIU Shuai, CHEN Xi-hong, WANG Che. Application of cognitive radio in frequency hopping com-munication[J]. Modern Defence Technology, 2013, 41(5):64-69. (in Chinese) [2] Wang T, Song L, Saad W, et al. Cooperative spectrum sensing in cognitive radio[J]. Frequenz, 2017, 67(3/4):93-98. [3] Shobana S, Saravanan R, Muthaiah R. Matched filter based spectrum sensing on cognitive radio for OFDM WLANs[J]. International Journal of Engineering & Technology, 2013, 5(1):142-146. [4] Ling X, Wu B, Wen H, et al. Adaptive threshold control for energy detection based spectrum sensing in cognitive radios[J]. IEEE Wireless Communication Letters, 2011, 1(5):1-5. [5] 熊辉,王鹰,张颖光,等. 基于延迟相乘和能量累积的DSSS信号参数估计算法[J]. 系统工程与电子技术, 2010, 32(10): 2227-2232. XIONG Hui,WANG Ying,ZHANG Ying-guang,et al. Parameter estimation of DSSS using delay-multiply and energy accumulation[J]. Journal of Systems Engineering and Electronics, 2010, 32(10): 2227-2232. (in Chinese) [6] 马彬, 方源, 谢显中. 一种基于信号循环平稳特征的抵御恶意模仿主用户攻击协作频谱检测算法[J]. 中国科学:信息科学, 2016,46(6):789-799. MA Bin, FANG Yuan, XIE Xian-zhong. Robust cooperative spectrum sensing against primary user emulation attacks based on cyclostationarity[J]. Scientia Sinica : Informationis, 2016,46(6):789-799. (in Chinese) [7] Chung C D,Polydoros A . Parameter estimation of random FH signals using autocorrelation techniques [J]. IEEE Transactions on Communications, 1995,43(2):1097-1106. [8] 高宪军, 李德鑫, 李娜,等. 基于功率谱对消的跳频信号检测算法[J]. 吉林大学学报:信息科学版, 2008, 26(3):238-243. GAO Xian-jun, LI De-xin, LI Na, et al. Algorithm for frequency-hopping signals detection based on suppressing power spectrum[J]. Journal of Jilin University: Information Science Edition, 2008, 26(3):238-243. (in Chinese) [9] 方志, 贾峰. 复杂电磁环境下跳频信号检测及拼接算法[J]. 无线电工程, 2010, 40(8):13-15. FANG Zhi, JIA Feng. Detection and mosaic algorithm of frequency-hopping signals in complicated electromagnetic environment[J]. Radio Engineering of China, 2010, 40(8):13-15. (in Chinese) [10] 齐佩汉, 司江勃, 李赞. 新型抗噪声不确定度谱分段对消频谱感知算法[J]. 西安电子科技大学学报:自然科学版, 2013, 40(6):19-24. QI Pei-han, SI Jiang-bo, LI Zan. Novel anti-noise uncertainty spectrum sensing algorithm based on power spectral density segment cancellation[J]. Journal of Xidian University:Natural Science, 2013, 40(6):19-24. (in Chinese) [11] 齐佩汉, 司江勃, 李赞. 基于功率谱分段对消频谱感知算法研究及性能分析[J]. 电子与信息学报, 2014, 36(4): 769-774. QI Pei-han, SI Jiang-bo, LI Zan. Research and performance analysis of spectrum sensing algorithm based on the power spectral density segment cancellation[J]. Journal of Electronics & Information Technology, 2014, 36(4): 769-774. (in Chinese) [12] 赵知劲, 吕曦, 郑仕链. 基于功率谱密度中段平均的频谱感知算法[J]. 电信科学, 2016, 32(7):53-60. ZHAO Zhi-jin, LYU Xi, ZHENG Shi-lian. Spectrum sensing algorithm based on average value of middle part of power spectral density[J]. Telecommunications Science, 2016, 32(7):53-60. (in Chinese) [13] 赵树杰, 赵建勋. 信号检测与估计理论[M]. 北京:电子工业出版社, 2013. ZHAO Shu-jie, ZHAO Jian-xun. Signal detection and estimation theory[M]. Beijing: Publishing House of Electronics Industry, 2013. (in Chinese) Time-domainCorrelationAlgorithmofCognitiveFrequencyHoppingBasedonPowerSpectrumCancellation LI Tong, MIAO Cheng-lin, LYU Jun (Department of Information Engineering, Academy of Armored Forces Engineering, Beijing 100072, China) TN925+.92 A 1000-1093(2017)09-1754-07 10.3969/j.issn.1000-1093.2017.09.012 2017-01-11 苗成林(1990—),男,博士研究生。E-mail: 644392162@qq.com 李彤(1964—),男,教授,博士生导师。E-mail:13601187076@163.com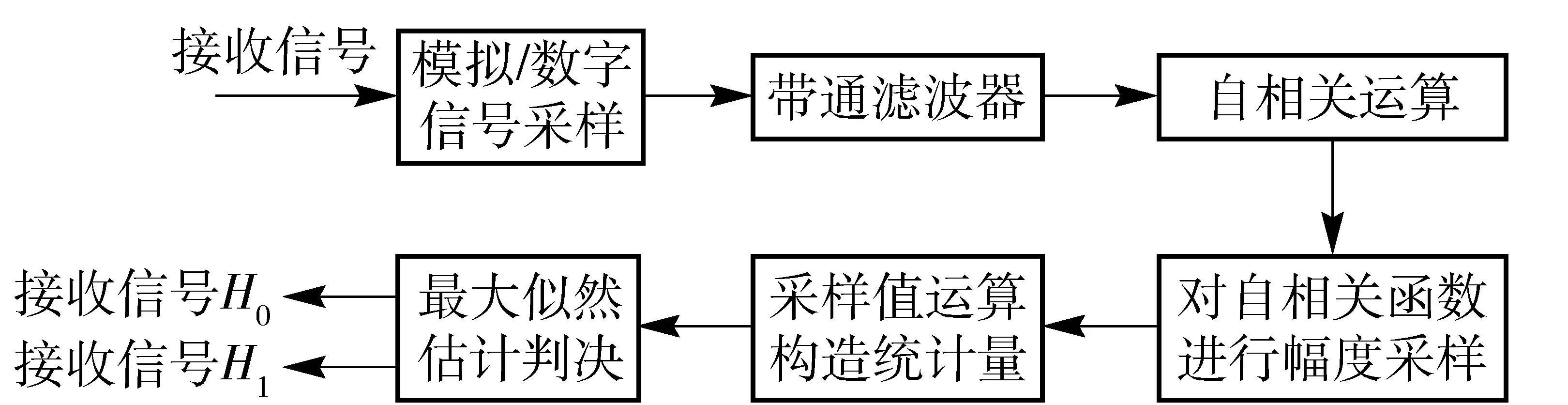
1 CHF系统模型

2 TCPC算法
2.1 TCPC算法过程
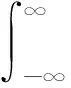

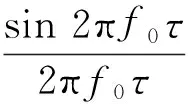

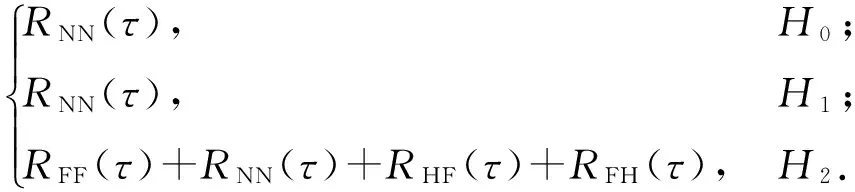




2.2 TCPC算法虚警概率和判决门限
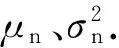
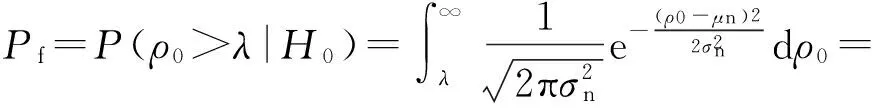
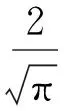
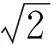

2.3 TCPC算法检测概率
3 TCPC算法过程仿真



4 TCPC算法性能分析
4.1 功率对消性能
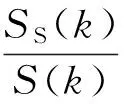

4.2 检测概率性能

5 结论
