扫频式干扰对调频多普勒引信的干扰机理研究

李泽， 闫晓鹏， 栗苹， 郝新红， 王建涛

(北京理工大学 机电动态控制重点实验室， 北京 100081)

扫频式干扰对调频多普勒引信的干扰机理研究

李泽， 闫晓鹏， 栗苹， 郝新红， 王建涛

(北京理工大学 机电动态控制重点实验室， 北京 100081)

为了揭示扫频式干扰对调频多普勒引信的干扰机理，在分析谐波定距调频多普勒引信的工作原理和扫频式干扰信号特征的基础上，理论推导了扫频式干扰信号作用下调频多普勒引信的响应过程，阐明了扫频式干扰对调频多普勒引信的干扰机理，并进行了仿真分析和试验验证。理论推导、仿真分析和试验表明：与点频干扰相比，扫频式干扰本身具有容错性，通过合理设置扫频参数，即可对谐波定距调频多普勒引信进行干扰，但引信加入各谐波间的严格逻辑时序判决措施后，其干扰效果会变差。

兵器科学与技术； 扫频式干扰； 调频多普勒引信； 逻辑时序判决

Abstract: In order to reveal the jamming mechanism of frequency sweep jamming to FM Doppler fuze, the response of FM Doppler fuze under the condition of frequency sweep jamming is deduced based on the analysis of the operational principle of FM Doppler fuze and the frequency sweep jamming signal feature. The jamming mechanism of frequency sweep jamming to FM Doppler fuze is elucidated, and the simulation analysis and experimental verification are carried out. Theoretical derivation, simulation analysis and experiment indicate that, compared with single-frequency jamming, frequency sweep jamming is fault-tolerant, and can successfully jam the FM Doppler fuze by reasonably setting the sweeping parameters; but its jamming effect will get worse when the FM Doppler fuze employs the strict logic timing judgment between different harmonics.

Key words: ordnance science and technology; frequency sweep jamming; FM Doppler fuze; logic timing judgment

0 引言

调频引信利用发射信号与回波信号的频率差来确定目标距离，距离测量并不依赖回波信号幅度，相对于连续波多普勒引信具有炸点散布小、定距精度高、抗干扰性能好等优点，在常规弹药中得到了广泛应用[1-3]。因此，伴随着电子对抗技术的快速发展，国内外均就调频引信的对抗技术进行了专门研究。资料显示，国外相关研究成果已达到装备实用阶段，如美国的“游击手”系统可成功对付M732、M734 和MK12近感引信炮弹、迫击炮和火箭弹的射击，干扰成功率为100%，其中M734采用的便是调频多普勒体制；俄罗斯的“SPR”干扰机据称能够对付在覆盖频率范围内80% 的引信，包括那些具有抗干扰措施的引信[4]。

目前，国内已经有学者对调频引信的对抗技术展开了一些研究，但尚停留在理论分析和样机研制阶段[5-9]。如文献[5]在分析有源干扰机理和模糊函数理论的基础上，提出用模糊函数切割法来测度线性调频连续波无线电引信的抗干扰性能；文献[6]提出一种基于分数阶傅里叶变换域相关的调频定距方法，以有效提高线性调频引信的抗噪声性能；文献[7]研究了基于数字射频存储的距离欺骗式干扰对线性调频引信的作用机理。

与此同时，国内相关研究单位针对调频多普勒引信展开了大量的干扰测试试验，试验结果表明，扫频式干扰可有效干扰调频多普勒引信，其中调幅扫频式干扰是对调频多普勒引信威胁最大的干扰波形，但国内外文献中针对该类干扰波形对调频多普勒引信作用的机理未见报道。

为此，本文选取应用广泛的谐波定距调频多普勒引信为研究对象，研究了扫频式干扰对调频多普勒引信的作用过程，以揭示扫频式干扰对调频多普勒引信的干扰机理。

1 谐波定距调频多普勒引信工作原理

典型谐波定距调频多普勒无线电引信的工作原理如图1所示[2-3]，图中fm为调制信号频率，m为谐波次数，fd为多普勒频率。系统工作过程为：经过三角波线性频率调制的发射信号遇到目标反射后由收发共用天线接收，回波信号与参考调频信号混频后输出包含目标距离信息的差频信号；差频信号经过带通滤波器，滤出包含第m次谐波的中频信号，然后与预定频率为mfm的参考信号进行2次混频和多普勒滤波；输出的多普勒信号经过后期的信号识别与逻辑判断后输出起爆信号。

图1 谐波定距调频多普勒引信原理框图Fig.1 Block diagram of FM Doppler fuze

三角波调频多普勒引信的发射信号通常表示为

(1)

式中：A表示发射信号幅度；fc表示信号载频；Δf表示信号单边调频带宽；T表示调制信号周期；T的倒数是调制信号频率fm；β=4Δf/T=4Δffm表示信号调频率；n为整数。因为很容易选取参数使得ΔfT为整数，所以相位项中含有ΔfT的项可省略不计。即(1)式所给出的发射信号可以简化为

(2)

目标回波信号可以表示为

Sr(t)=KSt(t-τ),

(3)

式中：K为信号从天线发射到接收过程中的衰减系数，它与探测目标的反射能力、方位和弹目相对距离R有关；τ=2R/c为回波延迟时间，c为光速。

回波信号被引信接收后，进入混频器并与耦合过来的载频信号混频，低通滤波后可得到中频信号为

(4)

式中：Am为混频器输出信号的幅值。此外，因为τ≪t，相对于时间t而言，其值可以忽略不计，故(4)式中已忽略不规则区。这样，中频信号Sm(t)表示成傅里叶级数的形式，有

(5)

式中：k(m,τ)为中频信号的傅里叶系数。

带通滤波后的中频信号与谐波发生器产生的m次谐波cos(2πmfmt)进行2次混频，并送入低通滤波器，输出m次谐波的多普勒信号Sd(t)为

Sd(t)=Adk(m,τ)cos (2πfdt),

(6)

式中：Ad为2次混频多普勒滤波后的信号幅值。

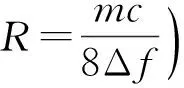
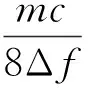
2 扫频式干扰信号分析

干扰机在对引信进行干扰时，扫频带宽必须覆盖引信的工作频带，扫频信号的载频会在一定频率范围内按一定规律来回摆动。设干扰机的扫频起始频率为fj0，扫频终止频率为fjN，扫频步长为Δfj，第n个扫频点的干扰信号载频为fjn，扫频总点数为N+1，则

fjn=fj0+nΔfj,n=0,1,…,N.

(7)

因为干扰机所发射的扫频干扰信号的载频是离散变化的，所以引信接收到的干扰信号表达式应该是一个分段函数，可以将其写成与门函数相乘的形式[10]。引信所接收到的扫频式干扰信号可表示为

Sj(t)=(Aj+f(t))cos (2πfjnt+φjn)gn(t)，
n=0,1,…,

(8)

Aj为干扰信号载波幅值；φjn为干扰信号起始相位，不失一般性，可设φjn=0；f(t)为干扰调制信号波形，扫频式干扰调制信号波形有各种形式，如正弦波、三角波、方波等，本文以正弦波调幅扫频干扰信号为例进行干扰机理分析，正弦波调制信号可以表示为f(t)=AjMcos (2πfjMt+φjM)，其中AjM为调制信号幅值，fjM为调制频率，一般设置为弹目交会过程中可能出现的多普勒频率，即fjM≈fd，φjM为调制信号起始相位，同样不失一般性，可设φjM=0. 正弦波调幅扫频式干扰信号的频谱如图2所示。

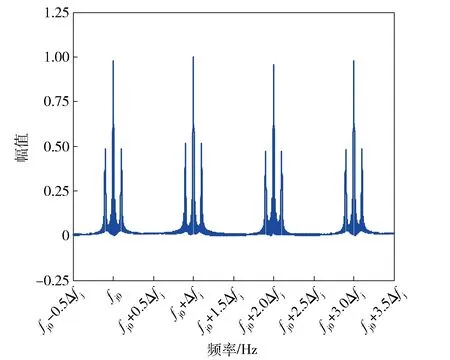
图2 正弦波调幅扫频式干扰信号的频谱Fig.2 Spectrum of sine AM frequency sweeping jamming signal

3 扫频式干扰对调频多普勒引信的干扰机理

为了简化公式推导，可将引信发射信号St(t)表示成傅里叶级数的形式：

(9)

根据前面的分析可知，扫频式干扰信号被引信接收后，首先要经过一次混频器，与耦合过来的发射信号进行混频，混频器的输出信号可以表示为

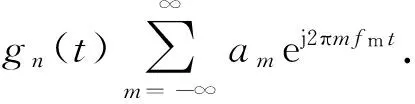
(10)

对(10)式进行化简，并通过低通滤波器滤掉高频信号，可得正弦波调幅扫频式干扰作用下引信中频信号的输出为

(11)

式中：M是低通滤波器通带内的谐波数。

扫频式干扰信号在每个扫频点的驻留时间Δt通常大于1 ms，远大于调制信号的周期，因此在一个驻留时间Δt内，各次谐波mfm都存在，即gn(t)对考虑当前驻留时间内中频信号特征的影响并不大。

第1次混频之后，混频器输出的干扰信号进入选定m次谐波的带通滤波器，与倍频器产生的m次谐波cos (2πmfmt)进行2次混频，并送入多普勒低通滤波器中提取多普勒信息。

设多普勒低通滤波器的截止频率为fd,l，正弦波调幅扫频式干扰信号通过选择参数，使得(12)式成立，则可以保证有干扰信号进入多普勒信号处理电路中。扫频干扰参数所需的条件为

m0fm≤|fjM+fΔ+nΔfj+mfm|≤m0fm+fd,l,

(12)

式中：n=0，1，…，N；m=0，±1，±2，…,±M；fΔ=fj0-fc为初始频率差，一般fΔ≫Δfj>fm≫fd,l≥fd≈fjM. 设m0为谐波定距调频多普勒引信所选取的定距谐波次数，对应的多普勒滤波器输出信号为

(13)

当干扰信号的能量同时满足多普勒信号处理电路所要求的阈值门限时，便可以实现对引信的干扰。

实际上，通过对比(6)式和(13)式，预定炸高处的目标回波与发射信号混频，所获得的中频信号相当于把回波信号μ个谐波分量的能量集中在所关注的m0次谐波上；而对于扫频式干扰，所获得的中频信号相当于把干扰信号的能量分散到μ个谐波上。因而相同能量下，扫频式干扰的干扰效果会随着调频指数μ的增大而减弱。

此外，由于(12)式中的m表示引信发射信号的谐波次数，与扫频式干扰信号的参数无关，因此若扫频干扰参数满足(12)式的条件，则一定满足：

(m0+l)fm≤|fjM+fΔ+nΔfj+mfm|≤
(m0+l)fm+fd,l,

(14)

式中：l=0，±1，±2，…. 由(14)式可知，扫频式干扰是同时进入引信各次谐波的滤波器通道的，其输出信号幅值的差异取决于对应发射信号的傅里叶系数am，并且根据(9)式可知，am≈am+l.

由此可知，若扫频参数设置合理，干扰信号会同时进入引信的各次谐波通道中，当干扰信号能量满足多普勒信号处理电路所要求的阈值门限时，便可成功干扰引信。然而，正常目标回波作用下，随着弹目距离的接近，一定是高次谐波先到达、低次谐波后到达。因此，若调频引信采用多次谐波联合定距，并在各谐波间增加严格的逻辑时序判决，则扫频式干扰在理论上干扰效果会变差。

4 仿真分析与讨论

为了验证上述结论，本文基于MATLAB分别构建了增加逻辑时序判决前后调频引信的仿真模型，并就扫频式干扰对两种调频引信的干扰效果进行了仿真验证。仿真工作参数设置如下：三角波调制频率fm=150 kHz；单边调频带宽Δf=15 MHz；调频指数μ=Δf/fm=100；多普勒频率fd=10 kHz；多普勒低通滤波器截止频率fd,l=20 kHz；所选择关注的谐波次数为2次和4次，对应2次混频的参考信号频率分别为300 kHz和600 kHz；信号幅值为1 V. 表1给出了不同干扰参数下，正弦波调幅扫频式干扰作用于调频多普勒引信的仿真结果。图3～图5分别给出了扫频步长Δfj为150 kHz以及扫频中心频率与引信载频频差分别为0 MHz和0.5 MHz时，两种调频引信2次、4次谐波通道多普勒滤波器的输出信号与引信启动信号。

表1 扫频式干扰作用于调频多普勒引信的仿真结果

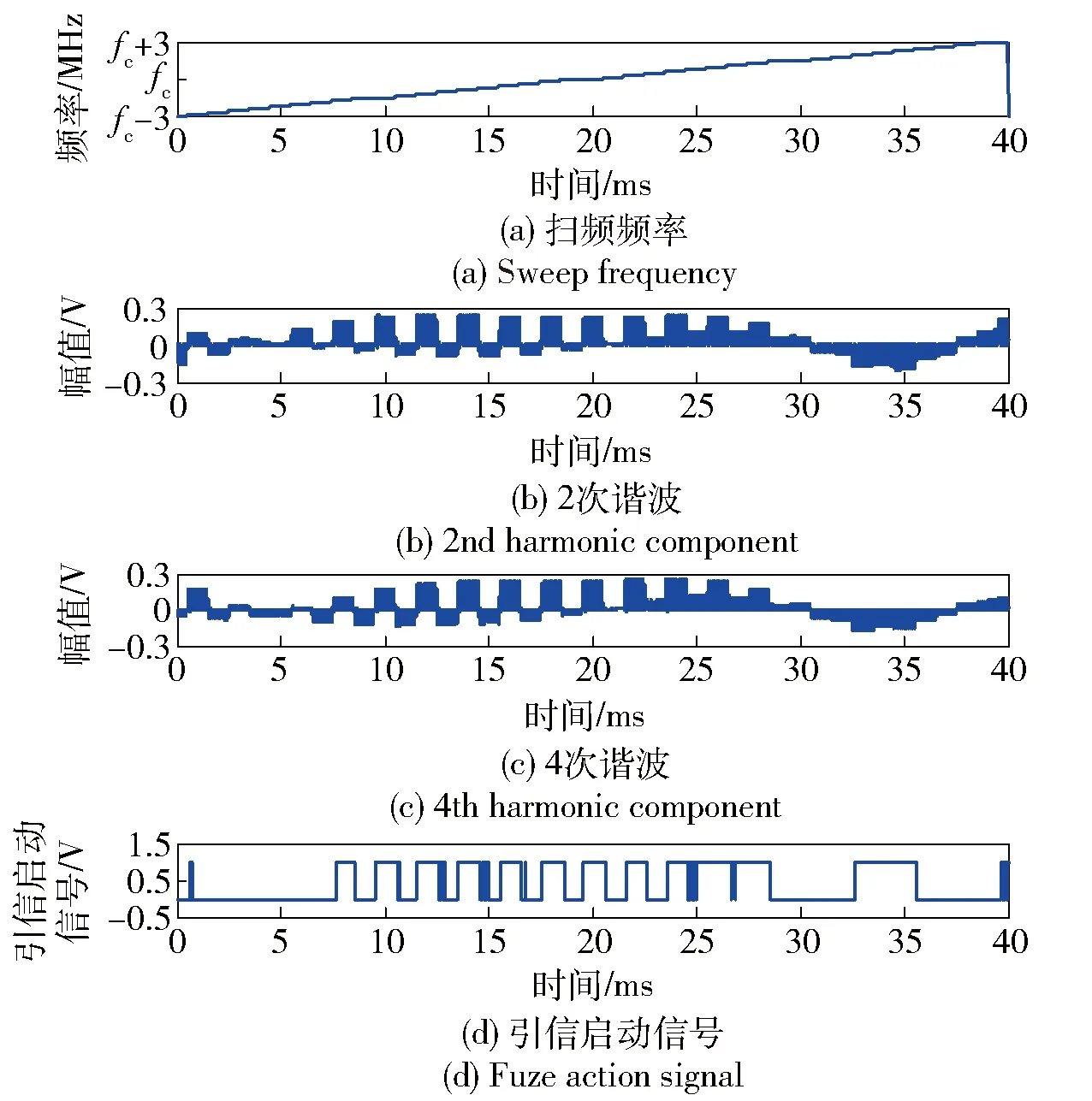
图3 调频引信响应情况(Δfj=150 kHz，无中心频差)Fig.3 Response of FM fuze for Δfj=150 kHz and no- center frequency difference

图4 调频引信响应情况(Δfj=150 kHz，中心频差0.5 MHz)Fig.4 Response of FM fuze for Δfj=150 kHz and center frequency difference of 0.5 MHz

图5 调频引信响应情况(Δfj=150 kHz，无中心频差，增加逻辑时序判决)Fig.5 Response of FM fuze for Δfj=150 kHz, no-center frequency difference, and logic timing judgment

理论推导与仿真分析表明：

1)仿真结果与理论推导相吻合，扫频带宽不必覆盖调频引信的工作带宽，扫频式干扰参数只需满足(12)式的条件，且干扰信号能量满足处理阈值，便可以成功干扰引信。一般情况下，扫频步长Δfj设置得越小，越容易干扰引信，但应尽量避免Δfj=kfm，其中k∈Z.

2)由图3、图5和表1可以看出，扫频式干扰信号是同时进入引信各次谐波通道内的，对于加入谐波间严格逻辑时序判决的调频引信来说，其干扰效果变差。

3)相对于点频干扰，扫频干扰信号在参数设置中具有容错性：点频干扰信号作用下，获得的中频信号频率成分集中在fj-fc+m×fm±fjM处，若干扰信号频率fj与引信载频fc存在偏差则不能干扰引信；扫频式干扰的工作频率fjn即使与引信载频fc存在偏差，也能在扫频步长设置合理的情况下，通过补偿n×Δfj来满足(12)式的条件，使干扰信号成功通过多普勒滤波器。

然而，由于常规弹药的体积限制，调频多普勒引信多为自差式收发引信，其工作载频会在一定范围内漂移，同时为规避同频干扰，引信工作的中心频率本身在设计时存在散布。综上所述，干扰信号的中心频率很难做到与引信的工作频率一致，因此，点频瞄准式干扰信号对调频多普勒引信没有干扰效果，而扫频式干扰有效。

5 试验验证

为了进一步验证前面理论推导和仿真分析所得的结论，本文在微波暗室内针对某调频多普勒引信和加入逻辑时序判决改造后的引信进行了干扰试验测试，试验中干扰系统与引信空间位置不变。干扰试验结果表明：点频干扰均不能使调频引信启动；调幅扫频式干扰在扫频参数合理的情况下可使调频引信启动，但针对改造后的调频引信(增加两谐波间严格逻辑时序判决电路)，其干扰效果会变差。其中，正弦波调幅扫频式干扰作用下调频引信的部分试验情况如表2所示。

表2 正弦波调幅扫频式干扰对调频多普勒引信的干扰效果

由表2的试验结果可以看出：扫频式干扰对加入逻辑时序判决引信的干扰效果明显弱于其对改造前引信的干扰效果；此外，扫频步长Δfj的大小对扫频式干扰的干扰效果影响比较大，且Δfj越小、越容易干扰，但当Δfj=150 kHz=fm时，则很难干扰引信。这与第3节和第4节的理论推导和仿真分析是一致的，进一步验证了所得结论的正确性。

6 结论

本文在明确谐波定距调频多普勒引信的工作原理和扫频式干扰信号特征的基础上，理论推导了扫频式干扰信号作用下调频多普勒引信的响应过程，揭示了扫频式干扰对调频多普勒引信的干扰机理，并针对所获干扰机理进行了仿真分析和试验验证。理论推导、仿真分析和试验验证表明：

1)扫频式干扰的扫频带宽不必覆盖调频引信的工作带宽，通过合理设置扫频参数，在满足一定条件(m0fm≤|fjM+fΔ+nΔfj+mfm|≤m0fm+fd,l)且干扰信号能量满足处理阈值的情况下，可以成功干扰引信。

2)一般情况下，扫频式干扰的扫频步长Δfj设置得越小，越容易干扰引信，但应尽量避免Δfj=kfm，其中k∈Z.

3)扫频式干扰相比于点频干扰本身具有容错性。点频干扰在干扰引信时需要干扰信号的工作频率与引信载频一致(由于引信自身的原因，很难做到二者一致)，而扫频式干扰的中心频率即便与引信载频存在偏差，也能在扫频步长设置合理的情况下成功通过多普勒滤波器，进而成功干扰引信。

4)扫频式干扰信号同时进入到引信各次谐波通道内，因而对于加入严格逻辑时序判决措施后的调频引信来说，其干扰效果会变差。

References)

[1] Stove A G. Linear FMCW radar techniques[J]. IEE Proceedings F-Radar and Signal Processing, 1992, 139(5): 343-350.

[2] 崔占忠, 宋世和, 徐立新. 近炸引信原理[M]. 第3版. 北京: 北京理工大学出版社, 2009:76-100. CUI Zhan-zhong, SONG Shi-he, XU Li-xin. Principle of proximity fuze[M]. 3rd ed. Beijing: Beijing Institute of Technology Press, 2009:76-100.(in Chinese)

[3] 赵惠昌. 无线电引信设计原理与方法[M]. 北京: 国防工业出版社, 2012:35-62. ZHAO Hui-chang. Fundamentals and methodology of radio fuze[M]. Beijing: National Defense Industry Press, 2012:35-62.(in Chinese)

[4] 张旭东, 郑世举, 余德瑛. 国外无线电引信干扰机的发展状况[J]. 制导与引信, 2004, 25(4): 22-25. ZHANG Xu-dong, ZHENG Shi-ju, YU De-ying. The development of radio fuze jammer abroad[J]. Guidance & Fuze, 2004, 25(4): 22-25.(in Chinese)

[5] 赵惠昌, 周新刚. 基于模糊函数切割法的线性调频连续波引信抗干扰性能测度[J]. 兵工学报, 2009, 30(12): 1591-1595. ZHAO Hui-chang, ZHOU Xin-gang. Anti-jamming performance evaluation of linear frequency-modulated continuous wave fuze based on ambiguity function incision[J]. Acta Armamentarii, 2009, 30(12):1591-1595. (in Chinese)

[6] 岳凯, 郝新红, 栗苹, 等. 基于分数阶傅里叶变换的线性调频引信定距方法[J]. 兵工学报, 2015, 36(5):801-808. YUE Kai, HAO Xin-hong, LI Ping, et al. Research on ranging method for linear frequency modulation radio fuze based on fractional Fourier transform[J]. Acta Armamentarii, 2015, 36(5):801-805.(in Chinese)

[7] 尹洪伟, 李国林, 隋鉴. 一种新的LFM引信距离欺骗干扰抑制算法[J]. 电讯技术, 2014, 54(1):52-57. YIN Hong-wei, LI Guo-lin, SUI Jian. A new LFM fuze distance deception jamming suppression arithmetic[J]. Telecommunication Engineering, 2014, 54(1):52-57.(in Chinese)

[8] 向程勇, 潘曦, 王正浩, 等. 基于求导比值的调频连续波测距方法[J]. 兵工学报, 2014, 35(5):613-619. XIANG Cheng-yong, PAN Xi, WANG Zheng-hao, et al. A new ranging method for FMCW fuze basd on the radio of the derivation[J]. Acta Armamentarii, 2014, 35(5):613-619. (in Chinese)

[9] 袁杰, 路翠华, 左传友, 等. 基于快速傅里叶变换的调频引信噪声干扰抑制[J]. 电子测量技术, 2013, 36(10): 31-33. YUAN Jie, LU Cui-hua, ZUO Chuan-you, et al. Anti-noise jamming for frequency-modulated fuze based on FFT[J]. Electronic Measurement Technology, 2013, 36(10): 31-33.(in Chinese)

[10] 张彪, 闫晓鹏, 栗苹, 等. 基于支持向量机的无线电引信抗扫频式干扰研究[J]. 兵工学报, 2016, 37(4):635-640. ZHANG Biao, YAN Xiao-peng, LI Ping, et al. Research on anti-frequency sweeping jamming of radio fuze based on support vector machine[J]. Acta Armamentarii, 2016, 37(4):635-640. (in Chinese)

JammingMechanismofFrequencySweepJammingtoFMDopplerFuze

LI Ze, YAN Xiao-peng, LI Ping, HAO Xin-hong, WANG Jian-tao

(Science and Technology on Electromechanical Dynamic Control Laboratory, Beijing Institute of Technology, Beijing 100081, China)

TJ43+4.1

A

1000-1093(2017)09-1716-07

10.3969/j.issn.1000-1093.2017.09.007

2017-02-13

国防“973”计划项目(613196)；国家自然科学基金项目 (61673066)

李泽(1989—)，男，博士研究生。E-mail:lzbuaa2007@163.com

闫晓鹏(1976—)，男，副教授，博士生导师。E-mail:yanxiaopeng@bit.edu.cn