地震后地下受损拱结构的抗爆炸能力研究
2017-10-12唐廷周健南
唐廷, 周健南
(1.海军勤务学院, 天津 300450; 2.陆军工程大学, 江苏 南京 210007)
地震后地下受损拱结构的抗爆炸能力研究
唐廷1, 周健南2
(1.海军勤务学院, 天津 300450; 2.陆军工程大学, 江苏 南京 210007)
为了评估地下结构的地震后抗爆炸能力,以边墙高3.0 m、半径3.0 m的半圆拱结构为模拟对象,假定了7种裂缝可能出现的位置。采用网格划分软件TrueGrid构建网格模型,基于LS-DYNA数值模拟分析地下拱结构在1条裂缝、2条裂缝和3条裂缝条件下的抗爆炸能力。分析结果表明:1条裂缝存在的条件下,地下拱结构的抗爆炸能力平均下降50%以上,裂缝的位置对地下拱结构的抗爆炸能力有明显影响,底板与边墙连接处的裂缝影响最大,拱顶正中的竖向裂缝影响最小;多条裂缝条件下的抗爆炸能力与单一裂缝相比没有明显区别,其抗爆炸能力的大小与各条裂缝单独存在时的最小抗爆炸能力相等。
爆炸力学; 地震; 地下结构; 数值模拟
Abstract: The evaluation of anti-blasting ability of underground structures has become a new research subject since earthquake can seriously damage the underground structures. A semicircular arch structure with radius of arch of 3.0 m and height of side wall of 3.0 m is simulated, and seven kinds of cracks at different locations are presumed. TrueGrid is used to construct a mesh model, and then the anti-blasting ability of underground arch structure is numerically simulated by LS-DYNA. The results show that the anti-blasting ability of underground arch structure with a crack is dropped by more than 50%. The anti-blasting ability of underground arch structure is affected by the location of cracks. The cracks between floor and side wall have the greatest effects on its anti-blasting ability and the cracks in arch crown have the least effects on its anti-blasting ability. The anti-blasting ability of arch structure with multi-cracks is not obviously different to that of arch structure with a single crack, and the anti-blasting ability is equal to the least value of anti-blasting ability when the cracks exist singly.
Key words: explosion mechanics; earthquake; underground structure; numerical simulation
0 引言
地震是地球上经常发生的一种自然现象,它是地壳在内、外应力的作用下,突然释放集聚的构造应力、产生震动弹性波,进而从震源向四周传播引起的震动。这种震动对地上结构的破坏已广为人知,然而它对地下结构也有着严重的破坏作用。例如,1995年日本的阪神地震造成神户市内地下结构发生严重破坏,其中地铁车站的破坏最重:中柱大量折断,顶板塌陷,侧墙出现大量宽大的裂纹[1-2];我国2008年的汶川地震也对地下结构造成了严重的破坏[3]。因此,对地下工程地震后的抗爆炸(简称抗爆)能力进行评估成为一个新的研究课题[3-4]。
地下拱结构的抗爆能力是防护工程的传统研究内容[5-7],而关于地下拱结构地震后抗爆能力的研究成果则较少,周健南等[3-4]将地震后拱结构简化为三铰拱,从理论上计算分析了拱结构地震后的抗冲击能力,给出了地震后拱结构的抗动载能力评估方法。在此基础上,本文以典型的地下拱结构为对象,采用先进的结构抗爆模拟程序LS-DYNA[8],研究地下拱结构在爆炸荷载作用下的响应与破坏规律,分析影响地下拱结构抗爆能力的主要因素。
1 地下拱结构
以图1所示的地下拱结构为研究对象,其中半圆拱部分的内径为3.0 m、拱厚为0.6 m、外径为3.6 m;边墙的高度为3.0 m、墙厚为0.6 m;底板的厚度为0.6 m. 半圆拱、边墙和底板均配有两排直径为16 mm、间距为120 mm的Q235钢筋,钢筋的保护层厚度为50 mm.

图1 地震后地下拱结构的破坏Fig.1 Damaged underground structure after earthquake
从图1可以看出,裂缝大多沿洞轴线伸展且已贯穿,因此可以取有限宽度的拱结构进行分析。结合拱结构内钢筋的布置情况,取0.12 m宽的拱结构为模拟对象,两个横断面定义为对称边界。本文的主要目的是分析裂缝对抗爆能力的影响,而裂缝处的抗剪和抗弯主要依赖于与裂缝面垂直的钢筋,故在模拟中可忽略拉筋和箍筋等其他钢筋的影响,只需在混凝土中设置两排直径为16 mm的Q235钢筋。
2 数值模拟方法
2.1 结构模型
如图2所示,根据汶川地震后地下结构破坏的特征,假设裂缝出现的位置有12种可能。其中:裂缝1位于底板正中间;裂缝2、裂缝12位于边墙与底板连接处,与边墙平行;裂缝3、裂缝11位于边墙与底板连接处,与底板平行;裂缝4、裂缝10位于边墙与半圆拱连接处,与底板平行;裂缝5~裂缝9相间分布于圆拱上,它们间隔的弧度均为30°,即裂缝7位于圆拱正中间。从实际的地震后破坏效果看,裂缝处的钢筋大多数未断裂,因此可以假定各模拟裂缝处的钢筋仍保持完好。
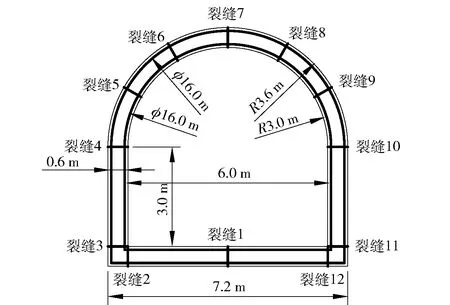
图2 地下拱结构Fig.2 Underground arch structure
如图3所示,为了模拟围岩与地下结构的相互作用,在拱结构周围建立宽38 m、高39 m的围岩区。其中拱结构顶端距围岩区域的上边界5.4 m,地下拱结构右侧距围岩区域的右边界15.4 m. 爆炸荷载p(t)以平面波的形式均匀作用于围岩的上边界。围岩底部节点的竖向位移被约束,其他为自由边界。
整个模型采用网格划分软件Truegrid划分有限单元网格,其中混凝土部分为六面体单元,钢筋为梁单元,单元尺寸约0.06 m,混凝土与钢筋之间的联结通过共用节点的方式实现。拱结构与围岩之间的相互作用通过定义接触实现,其中设静摩擦系数为0.3、动摩擦系数为0.2.

图3 围岩区域及地下结构位置Fig.3 Region of wall rock and location of underground structure
2.2 材料模型
混凝土采用Holmquist-Johnson-Cook(HJC)本构模型[9],模拟选取的参数见表1[10].其中失效类型参数取为0.004,表示混凝土材料的有效塑性应变达到该值时单元失效。
钢筋假定为45号钢,采用随动强化双线性弹塑性模型(MAT_PLASTIC_KINEMATIC)进行描述,并通过动态塑性本构准则模型模拟钢筋的应变率效应。钢筋屈服应力可表示为
(1)


表1 混凝土HJC模型参数

表2 钢筋模型参数
围岩在地下拱抗爆过程中的主要作用是提供准确的冲击荷载以及约束拱结构的变形与破坏,因此本文不考虑围岩自身的破坏,将围岩假定为弹性材料,以简化模拟过程。模拟中设围岩的密度为2 750 kg/m3,弹性模量为8.0 GPa,泊松比为0.19.
2.3 爆炸冲击波荷载
炸药在岩石中爆炸所产生的冲击波荷载可以减化为三角形荷载,以峰值压力pm=3 MPa的冲击荷载为例,假定其升压时间t+=2 ms,压力作用时间ts=25 ms. 且假设当峰值压力改变时,其升压时间和压力作用时间均按线性比例改变。图4给出了峰值压力pm分别为3 MPa、4 MPa、5 MPa时爆炸冲击波荷载的时程曲线。数值模型中,爆炸冲击波荷载直接施加至围岩的上边界,在LS-DYNA中的关键字为*LOAD_SEGMENT.

图4 冲击波荷载时程曲线Fig.4 Time-history curves of shock wave load
3 未损地下拱结构的抗爆能力
下面采用试算的方法评估地下拱结构的抗爆能力,模拟计算的时间为4 s(根据多次试算的结果,4 s内结构的变形与破坏已趋于稳定)。通过调整冲击荷载的大小(调整精度为0.1 MPa)来观察数值模拟后的拱结构是否破坏,得到临界破坏荷载。破坏的标准为同一位置处的两排钢筋是否全部断裂。
以地震前地下拱结构为例,取冲击荷载峰值压力pm=10.0 MPa(t+=6.67 ms,ts=83.33 ms),如图5所示:当冲击荷载作用0.1 s时底板开始受反射波的影响,随后底板向上翘起,在底板中部和拱脚处产生应力集中,使应变增大,当累积应变达到材料极限后经过3.0 s,底板中部断裂并继续向上运动,导致拱脚处也完全断裂(见图6(a));取冲击荷载峰值压力pm=9.0 MPa(t+=6.00 ms,ts=75.00 ms),
冲击荷载作用4.0 s后,地下拱结构整体保持完整(见图6(b))。因此震前地下拱结构的承载能力介于10.0~9.0 MPa之间。
然后以精度0.1 MPa调整冲击荷载的峰值大小,观察模拟得到的结果。取冲击荷载峰值压力pm=9.5 MPa(t+=6.33 ms,ts=79.12 ms),冲击荷载作用4.0 s后,地下拱结构的底板中间混凝土和两层钢筋完全断裂(见图6(c));取冲击荷载峰值压力pm=9.4 MPa(t+=6.27 ms,ts=78.33 ms),冲击荷载作用4.0 s后,底板中间混凝土部分破坏,但整体保持完整(见图6(d))。根据以上多次试算,可以认定地震前该地下拱结构的承载能力为9.4 MPa,其抗爆能力可用对应的冲量表示为368 kPa·s.

图5 地震前地下拱结构的破坏过程(pm=10.0 MPa)Fig.5 Damage process of underground arch structure before earthquake (pm=10.0 MPa)
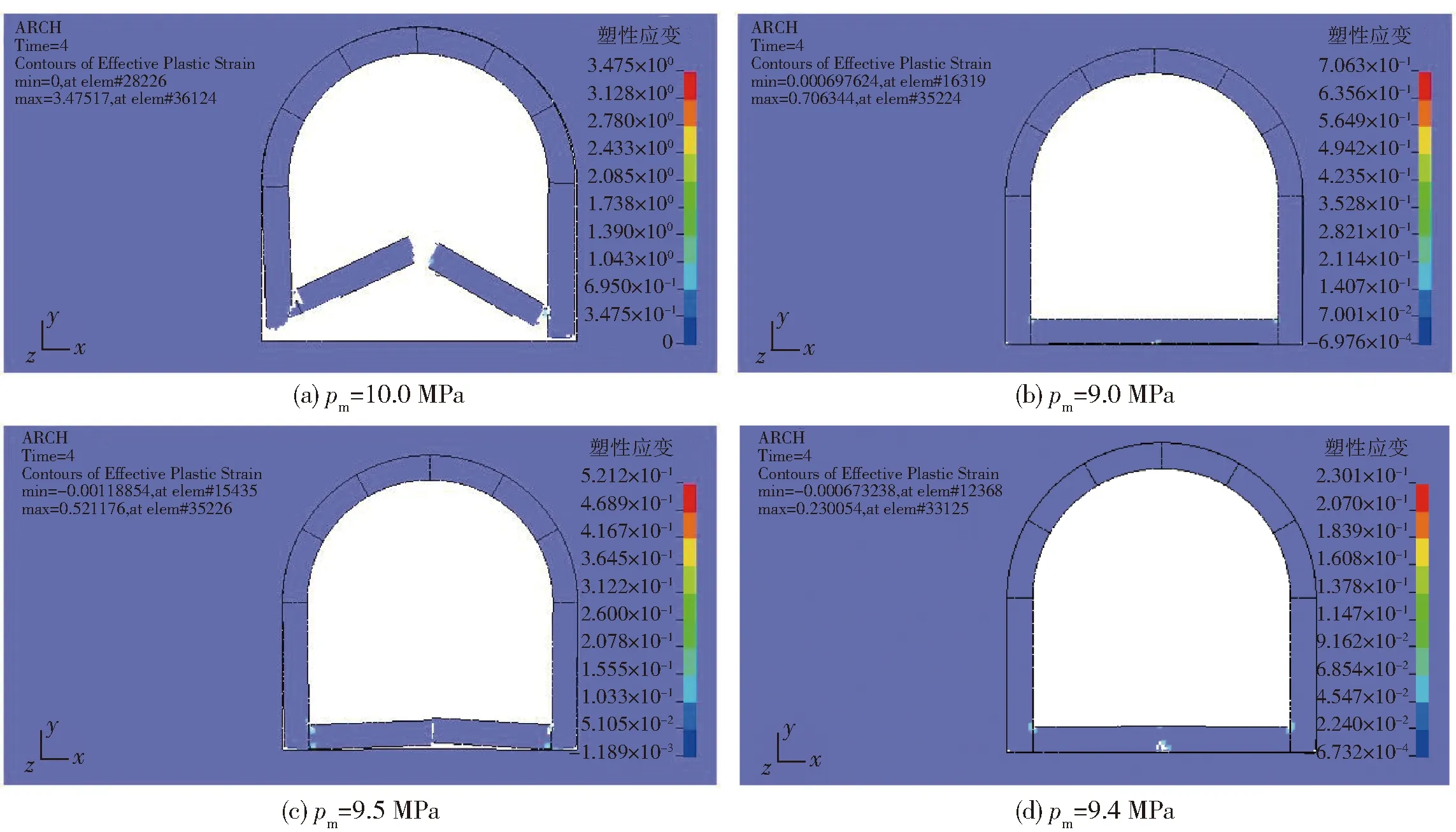
图6 不同冲击荷载峰值压力下的地震前地下拱结构响应Fig.6 Response of underground arch structure before earthquake at peak pressures of shock load
4 单一裂缝地下拱结构的响应
下面分析地震作用后有1条裂缝的地下拱结构在爆炸荷载作用下的响应规律。根据对称性,只需分析裂缝1~裂缝7对地下拱结构抗爆能力的影响,分别对应工况1~工况7. 模拟的方法与无裂缝的情况相同。由于模拟的工况较多,图7只给出了地下拱结构刚好破坏的变形图。
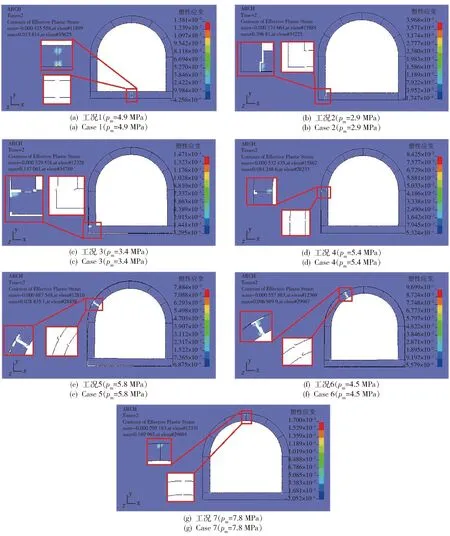
图7 不同工况条件下的地震后1条裂缝地下拱结构响应Fig.7 Response of underground arch structure with a crack after earthquake in different cases
7种不同位置裂缝的地下拱结构的抗爆模拟结果比较如表3所示。其中α表示地下拱结构地震后的剩余抗爆能力与地震前抗爆能力的比值,称为剩余比。它可以很好地衡量裂缝对抗爆能力的影响,如图8所示:裂缝2和裂缝3的剩余比α≈0.1,表明其影响较大;裂缝7的剩余比α≈0.7,表明其影响较小。7种裂缝的平均剩余比α≈0.3,即有1条裂缝的情况下,地下拱结构的抗爆能力下降50%以上。

表3 模拟结果的比较

图8 裂缝位置对抗爆能力的影响Fig.8 Effect of crack location on anti-blasting ability
5 与理论计算结果的比较
目前,关于地震后受损地下拱结构抗爆能力研究的文献较少,可供比较的只有周健南等[3-4]的部分理论计算结果,没有相关的试验结果可供参考。为了验证数值模拟结果的正确性,将本文模拟结果与文献[4]结果进行比较。
文献[4]从拱脚推力的角度考虑拱的承载能力:“在裂缝穿透截面的条件下,配筋率较高时地震后结构承载能力下降60%~70%”;工况3时的承
载能力为3.3 MPa,相对于地震前地下拱结构的承载能力(9.4 MPa)下降了64.9%,与理论计算非常吻合。特别是后续工况17的模型与文献[4]中假定的两铰拱结构模型类似,模拟得到的承载能力为3.3 MPa,下降了64.9%,与理论计算结果一致,表明数值模拟结果是较准确的。
6 多个裂缝地下拱结构的响应
下面分析多条裂缝对地下拱结构抗爆能力的影响。以图1为基础,假定有2条裂缝,根据概率论,不同裂缝组合的工况共有12×11=132种,考虑到对称性,需要模拟的工况将超过60种。如果有3条裂缝,则需要模拟的工况将超过100种,计算的工作量无疑是巨大的,因此有必要进行适当且合理的简化。
从以上研究和图8可以看出,裂缝2和裂缝3的影响是相似的,而且裂缝2和裂缝3一般不会同时出现,因此后面的模拟只考虑裂缝3的影响。而拱侧上的裂缝4、裂缝5和裂缝6的影响也是相似的,后面的模拟中将取裂缝5为代表,研究它与其他裂缝结合出现时的影响;裂缝4、裂缝5和裂缝6也可能同时出现,这一情况需要单独进行模拟分析。因此只需要模拟12种工况。
3条裂缝的工况组合数目更多,现在仅分析3条裂缝相邻分布的情况,考虑到裂缝2和裂缝3一般不会同时出现,基于拱结构的对称性,只需模拟6种工况。为了与理论计算的结果进行比较,还增加了工况37,即共模拟7种工况。
2条裂缝12种工况和3条裂缝7种工况的组合方式和模拟结果分别汇总如表4和表5所示,工况组合的编号从11~22,其中后3种工况模拟的是裂缝4、缝裂5和缝裂6同时存在2条裂缝的情况,表4和表5中最后一行为工况组合中裂缝单独出现时的抗爆能力。

表4 2条裂缝的组合方式与模拟结果

表5 3条裂缝的组合方式与模拟结果
图9、图10分别为2条裂缝、3条裂缝在爆炸荷载作用下的变形图。对2条裂缝和3条裂缝共19种工况的数值模拟结果进行分析可以发现:
1) 多条裂缝存在的条件下,地下拱结构的抗爆能力由其中对抗爆能力影响最大的裂缝决定,存在“木桶”现象(木桶装水的多少由最短的一块板决定)。即多条裂缝存在时,地下拱结构从最薄弱的位置开始破坏,最薄弱的位置就是影响最大的某条裂缝。

图9 不同工况条件下的地震后2条裂缝地下拱结构响应Fig.9 Responses of underground arch structure with two cracks after earthquake in different cases
2)模拟的多条裂缝工况共有19种,每种工况的抗爆能力与工况组合裂缝单独出现时的抗爆能力相比:抗爆能力下降的有5种,平均下降6.0 kPa·s,最大下降13.0 kPa·s;抗爆能力上升的有8种,平均上升6.75 kPa·s;还有6种工况保持不变。与地震前地下拱结构368 kPa·s相比,说明多条裂缝时的抗爆能力与单一裂缝时的抗爆能力没有显著区别。

图10 不同工况条件下的地震后3条裂缝地下拱结构响应Fig.10 Responses of underground arch structure with three cracks after earthquake in different cases
7 结论
1)数值模拟的结果与理论计算的结果基本吻合,符合地震后地下拱结构抗爆能力的变化规律。
2)裂缝位置对于地震后地下拱结构的抗爆能力影响较大。当裂缝在拱顶正中时,其对拱结构抗爆能力的影响最小,大约剩余70%的抗爆能力;当裂缝处于拱脚位置时,其对拱结构抗爆能力的影响较大,大约剩余10%左右,其中裂缝垂直于底板时影响最大。
3)多条裂缝存在的条件下,地下拱结构的抗爆能力由其中对抗爆能力影响最大的裂缝决定。而且多条裂缝时的抗爆能力与单一裂缝时的抗爆能力没有显著区别。
4)影响地震后地下拱结构抗爆能力的因素还有很多,本文仅分析了裂缝位置和多条裂缝组合的影响。下一步可详细分析裂缝特征(缝宽、摩擦系数)和围岩破坏状况等对地震后地下拱结构抗爆能力的影响,以进一步揭示地震后地下拱结构的抗爆与毁伤机理。
另外,本文假定的爆炸荷载作用方向为垂直向下,实际的爆炸荷载作用一般存在一定的角度,当角度过大时(如水平方向的爆炸荷载),会对拱结构的抗爆能力产生一定的影响,但影响的定量规律需要通过后续的研究得出。
References)
[1] Hayashi Y, Tamura K, Mori M, et al. Simulation analyses of buildings damaged in the 1995 Kobe, Japan, earthquake considering soil-structure interaction[J]. Earthquake Engineering and Structural Dynamics, 1997, 28 (4): 371-391.
[2] Nakamura Susumu, Ezaki Jyunich, Suetomi Iwao, et al. Investigation, analysis and restoration of the collapsed Daikai subway station during the 1995 Hyogoken Nambu earthquake[C]∥ 3rd Kansai International Geotechnical Forum. Japan: Japan Society of Civil Engineering, 1997.
[3] 周健南,金丰年,范华林,等.震后地下拱结构的抗冲击波动载能力评估[J].工程力学,2012,29(2):159-164,171. ZHOU Jian-nan, JIN Feng-nian, FAN Hua-lin, et al. Residual dynamic resistance of seismic damaged underground arch[J]. Engineering Mechanics, 2012, 29(2): 159-164, 171.(in Chinese)
[4] 周健南,范华林,金丰年,等.非均布荷载作用下震后地下拱结构抗动载能力评估[J].工程力学,2012,29(增刊1):119-123,140. ZHOU Jian-nan, FAN Hua-lin, JIN Feng-nian, et al. Residual dynamic resistance assessment of seismic damaged underground arch under non-uniform explosion loading[J]. Engineering Mechanics, 2012, 29(S1): 119-123, 140.(in Chinese)
[5] 范鹏贤,王明洋,冯淑芳,等.直墙拱顶地下结构受爆炸地震波作用的动力响应[J].振动与冲击,2014,33(22):183-187. FAN Peng-xian, WANG Ming-yang, FENG Shu-fang, et al. Dynamic response of underground straight-wall-round-arch structure subjected to explosion seismic wave[J].Journal of Vibration and Shock, 2014,33(22): 183-187.(in Chinese)
[6] 王光勇,顾金才,陈安敏,等.锚固洞室在顶爆作用下破坏形式及破坏过程研究[J].岩土工程学报,2015,37(8):1381-1389. WANG Guang-yong, GU Jin-cai, CHEN An-min, et al. Failure modes and process of tunnels reinforced by rockbolts under top explosion[J].Chinese Journal of Geotechnical Engineering, 2015, 37(8): 1381-1389.(in Chinese)
[7] 谢威,蒋美蓉,周健南,等.空爆作用下复合材料加固圆拱动力响应数值模拟[J].武汉理工大学学报,2014,36(1):135-139.XIE Wei, JIANG Mei-rong, ZHOU Jian-nan, et al. Numerical simulation on dynamic response of circular concrete arch strengthened with composite materials under air blast loading[J].Journal of Wuhan University of Technology, 2014, 36(1): 135-139.(in Chinese)
[8] 康婷,许金余,白应生,等.爆炸冲击荷载作用下拱结构的弹塑性动力响应研究[J]. 兵工学报,2013,34(9):1097-1102. KANG Ting, XU Jin-yu, BAI Ying-sheng, et al. Elastic-plastic ana-lysis on dynamic response of arch subjected to explosive impact[J]. Acta Armamentarii, 2013, 34(9): 1097-1102. (in Chinese)
[9] Tu Z G, Lu Y. Evaluation of typical concrete material model used in hydrocodes for high dynamic response simulations[J].International Journal of Impact Engineering, 2009, 36(1): 132-146.
[10] 贾彬,李正良,陶俊林,等.混凝土SHPB试验数值模拟研究[J].固体力学学报,2010,31(增刊1):216-221. JIA Bin, LI Zheng-liang, TAO Jun-lin, et al. Research on numerical simulation of SHPB concrete tests[J].Chinese Journal of Solid Mechanics, 2010, 31(S1): 216-221.(in Chinese)
[11] 田力,朱聪,王浩,等.碰撞冲击荷载作用下钢筋混凝土柱的动态响应及破坏模式[J].工程力学,2013,30(2):150-155. TIAN Li, ZHU Cong, WANG Hao, et al. Dynamic response and failure modes of RC columns under impact[J].Engineering Mechanics, 2013, 30(2): 150-155.(in Chinese)
StudyofAnti-blastingAbilityofDamagedUndergroundArchStructureafterEarthquake
TANG Ting1, ZHOU Jian-nan2
(1.Naval Logistics College of PLA, Tianjin 300450, China; 2.Army Engineering University, Nanjing 210007, Jiangsu,China)
TU93+2; O383+.2
A
1000-1093(2017)09-1736-09
10.3969/j.issn.1000-1093.2017.09.010
2016-07-28
国家自然科学青年基金项目(51308544); 解放军理工大学预先研究基金项目(KYDXZLXY1301)
唐廷(1980—), 男, 讲师, 博士后。 E-mail:kublai@126.com
周健南(1979—), 男, 副教授, 博士。 E-mail:zjn_0414@163.com
