基于SVR的互联液压缸力学性能预测∗

汪若尘，叶 青，丁彦姝，俞 峰，陈 龙

基于SVR的互联液压缸力学性能预测∗

汪若尘，叶 青，丁彦姝，俞 峰，陈 龙

(江苏大学汽车与交通工程学院，镇江 212013)

为进一步研究实际工况下非线性因素对互联液压缸力学特性的影响，对互联液压缸进行了力学性能台架试验，分析了互联液压缸的非线性因素对其力学输出的影响。鉴于传统数学模型无法准确反映互联液压缸动力学特性，并为减小传统支持向量机算法数据回归拟合误差，引入不敏感损失函数，构建互联液压缸力学性能回归型支持向量机预测模型进行预测，并将预测结果与试验数据进行对比。结果表明，采用回归型支持向量机预测模型具有更好的预测精度，为揭示互联悬架力学特性提供新的研究思路。

互联液压缸；力学性能；预测模型；回归型支持向量机

Keywords:interconnected hydraulic cylinder； mechanical performance； prediction model； regression support vector machine

前言

近年来，全世界车祸事故报道越渐频繁，2004年NHTSA提供的数据[1]显示，美国近1/3的车祸事故起源于车身侧翻，尤其体现在货车、SUV和客车等高质心车辆上，而悬架在保证车辆安全方面起着关键作用[2-3]。针对车辆侧翻问题，大量学者进行了相应研究，并设计了不同悬架结构，其中液压互联悬架(hydraulic interconnected suspension，HIS)系统由于其卓越的操纵稳定性能和良好的行驶平顺性能，受到了国内外学者广泛关注。

文献[4]中最早提出了油管互联减振器，并阐述了多轮之间可能存在的互联方式。文献[5]中基于液压互联悬架对比试验，建立了简单的2自由度车辆微分方程。文献[6]和文献[7]中提出了一种抗侧倾液压互联悬架，并针对紊流阀损和缸内流体压缩进行了理论分析，但缺乏对传递路线损失、流体管内压缩、流体惯性和液体弹性波效应的研究与试验验证。文献[8]中将网络综合理论应用于传统被动互联悬架系统，提出了一种机械导纳矩阵，并针对3种阻尼结构进行理论分析。文献[9]中则基于网络综合理论提出了刚度和阻尼解耦，但对HIS动力学研究不足，因此网络综合理论应用合理性无法判定。2005年，文献[10]中综合现有研究成果对互联悬架进行了理论定义，证实了互联液压缸能有效提升悬架的防侧倾性能，并在此基础上对互联液压缸力学模型进行了理论研究和公式推导。

然而上述液压互联悬架研究均以理想互联液压缸耦合模型进行相应研究，忽略了实际结构中互联液压缸系统内泄漏、内摩擦和空程畸变等非线性因素对液压缸力学性能的影响。文献[11]中理论分析了液压缸非线性因素对悬架性能的影响，并运用电子网络理论和系统综合方法理论研究被动液压互联悬架的特性，但研究忽略了流体管路的动态特性和流体的可压缩性；文献[12]～文献[15]中考虑二维可压缩流体模型对液压互联悬架稳态特性的影响，进一步对模型进行了完善。

综上所述，目前互联液压缸的非线性研究模型较为简单，无法全面反映实际工况下互联液压缸力学特性。因此，本文中通过互联液压缸力学性能台架试验，深入研究非线性因素对互联液压缸力学性能影响机理，并引入支持向量机预测模型对互联液压缸力学性能进行预测。同时为了解决传统SVM对数据回归拟合精度问题，引入不敏感损失函数ε，构建互联液压缸回归型支持向量机预测模型，并利用台架试验对所建模型进行验证。

1 液压互联悬架

1.1 互联液压缸工作原理

互联液压缸结构如图1所示。

液压互联悬架作用效果取决于互联液压缸，当左液压缸两端受到拉力，右端液压缸受到压力时(或者左端受压右端受拉)，左右液压缸压力腔相对，进而产生作用力阻止左右液压缸运动趋势；当两端同时受压或者受拉时，左右液压缸，左右油液交互，基于左右端拉升(压缩)程度差产生反向作用力，从而实现全局防侧倾效果。同时，为了防止互联液压缸运行时引起油液波动，引入蓄能器，以稳定回路内油液压力，从而提高液压缸力学特性。

1.2 液压互联悬架结构

图1 互联液压缸结构示意图

基于图1所示结构，理想互联液压缸力学模型[16-18]可表示为

式中A1和A2分别为有杆腔和无杆腔的有效面积。

理想情况下，互联液压缸系统密封良好，且油液不可压缩，忽略液体弹性波效应，流体传递压力损失主要与管道压降、蓄能器阀压降和蓄能器压力相关，其中管路压降[16-17]为

式中:d为流体管道内径；ρ为流体密度；L为管道长度；ν为流体的运动黏度。

蓄能器阀压降[17-20]为

其中:

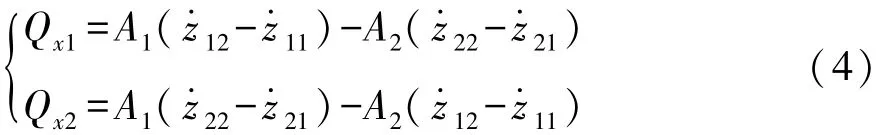
式中:Cq为流体流量系数；Ac为蓄能器出口阻尼阀开口面积；Qxi为蓄能器吸收的液体流量。

蓄能器内压力与体积关系为

式中:p0和V0为蓄能器初始压力和体积；p和V为蓄能器工作压力和体积；n为绝热指数，n＝1.4。

基于流体体积守恒原理[21]，蓄能器在外部压力下气囊容积为

其中:

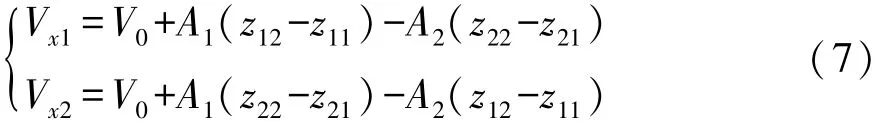
综合式(5)～式(7)，蓄能器工作压力为

以蓄能器工作压力为平衡点，探究液压缸工作压力，忽略缸内液体产生的压降，则压力p1，p2，p3和p4为

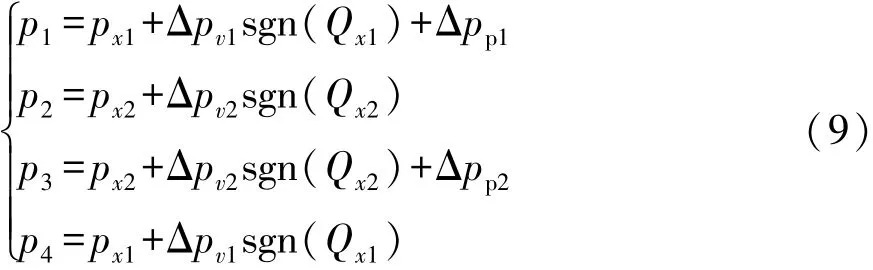
由以上公式可以得出，互联液压缸作用力取决于阀开口面积、管道长度与直径、液压缸有效作用面积、流体参数和蓄能器参数，因此可以通过以上设计参数以获取符合工程需要的液压互联悬架。本文中研制的互联液压缸具体结构参数如表1所示。

表1 结构参数

2 台架试验

2.1 试验方案

纯互联液压缸由于结构限制，在INSTRON8800单通道液压激振台上试验时，设计选取其中某一液压缸作为受力对象安装于激振台上，另一液压缸空载，具体实验方案如图2所示。

在液压互联悬架试验中，采用正弦激励信号作为输入，取液压缸作用力作为输出，试验频率取0.1，0.5，1，3，5，7，9，11，13 和 15Hz，其中，0.1-5Hz取幅值为10mm，7-15Hz取幅值为5mm。试验中，通过激振头自带的力传感器实时采集力信号并存储到控制台。

2.2 试验结果

图2 互联液压缸结构试验图

表2给出了互联液压缸的力学性能试验幅值与理论幅值对比结果。

表2 力学性能对比

图3给出了激振频率为0.1，5和9Hz时互联液压缸力学响应的时域图。

由表2和图3可以看出，互联液压缸的力学性能输出在正弦的基础上呈现出较强的非线性特点。在低频阶段，互联液压缸由于存在缸内摩擦，互联液压缸的力学响应在正弦波动基础上部分表现为阶跃输出，如第1.12和1.22s等，且由于左右液压缸耦合作用和缸内流体阻尼效应，其力学相应无法表现成近似方波。

由表2可以看出，随着激励频率的增加，理论幅值表现出近似线性增加，且增长速度比实际试验幅值更为明显，这是由于实际试验中系统存在左右液压缸耦合效应和非线性干扰，同时高频时试验得到的力学输出幅值与理论幅值较为接近。从图3可以详细看出，互联液压缸的力学输出在周期性正弦曲线的基础上出现了许多非线性特点，包括互联液压缸系统耦合作用、系统内泄漏与内摩擦、流体特性导致的空程畸变、流体在系统内流动产生的黏滞阻尼和流体特有的弹性波效应。其非线性影响具体表现在试验输出曲线的平衡位置和波峰位置。

综上可知，互联液压缸的力学性能输出受系统内摩擦、内泄漏和流体特性等综合影响，仅从数学解析的角度无法进行准确描述，因此，本文中拟运用回归型支持向量机对互联液压缸进行力学性能预测。

图3 力学响应

3 回归型支持向量机模型预测

回归型支持向量机(SVR)[21-24]是一种针对模型回归的机器学习算法，通过引入不敏感损失函数ε，使所训练样本离寻找到的最优分类面的距离最小，同时SVR基于结构风险最小化准则，提高了模型的泛化能力，因此在模型预测上得到了广泛的应用。

此外SVR在有限样本情况下可获得最优预测数据，且通过算法最终将转化为一个二次规划问题，在理论上可得到全局最优解。而互联悬架力学性能预测问题为小样本问题，完全适合用SVR算法进行研究，所以本文中采取SVR对互联悬架力学性能进行预测。

首先，建立含有n个训练样本的训练样本集{(xi，yi)，i＝1，2，…，n}，其中，xi(xi∈Rd)是第 i个训练样本的输入列向量，yi∈Rd为对应的输出值。

为简化统计模型计算量，引入模型预测正确率较高的径向基核函数代替传统统计学模型进行运算，其核函数为

其次引入线性不敏感损失函数ε进行误差判定:

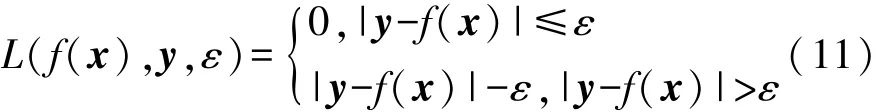
其中回归函数f(x)表达式为

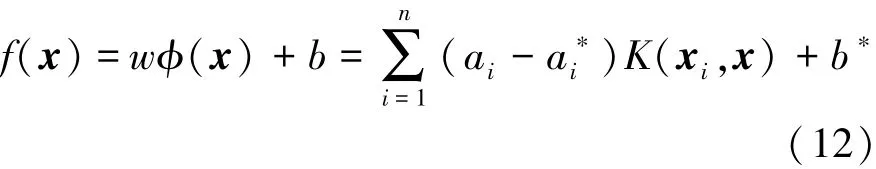
将松弛变量 ξi，ξ∗i和惩罚因子C引入回归函数，则原回归函数中w和b可表示为

引入均方误差E和决定系数R2对所建立的SVR回归模型预测效果进行判断，其表达式为

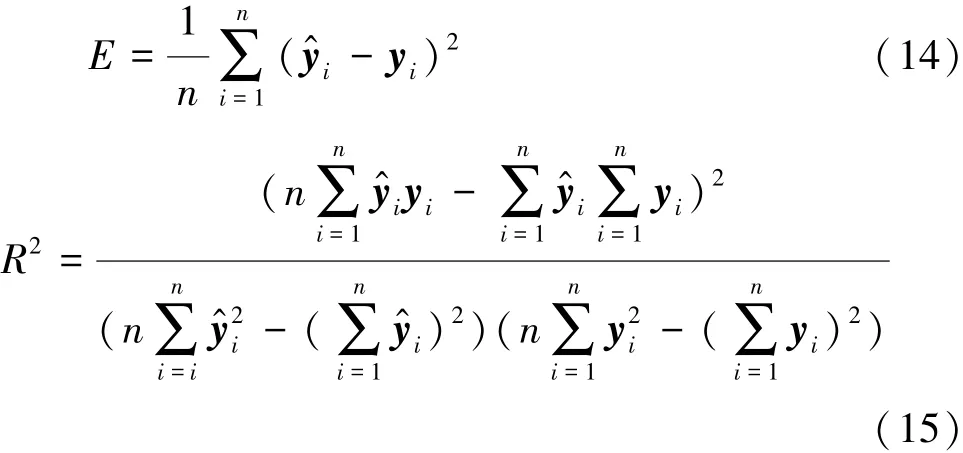
针对样本中各变量值的数量级差异问题，对数据进行归一化处理。考虑到惩罚因子C和核函数方差g对回归模型性能影响较大且训练样本数量少，利用交叉验证[26]方法对惩罚因子C和核函数方差g进行寻优，经求解，得到惩罚因子C的取值为0.5，核函数中的方差g取值为0.6。

在回归模型建立后，输入训练样本集，以左端互联液压缸在时间序列中某时间段的位移输入和速度输入作为输入样本，以左端互联液压缸两端点的力信号作为输出样本，其中互联液压缸的样本输入为正弦激励输入，为提高预测精度，每个工况采集120组数据点在不同频率下对互联液压缸的力学性能进行预测输出。

4 结果分析

选取5Hz工况下120组样本数据集作为测试对象，随机抽取其中80组样本数据作为回归型支持向量机训练样本，剩余40组样本数据作为测试数据，其数据集训练误差如图4所示。

图5为激振频率为0.5，5和9Hz下的互联液压缸力学性能预测图。基于式(14)和式(15)判定，其力学预测结果如表3所示。

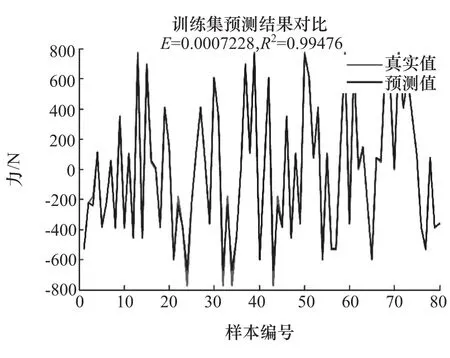
图4 训练误差

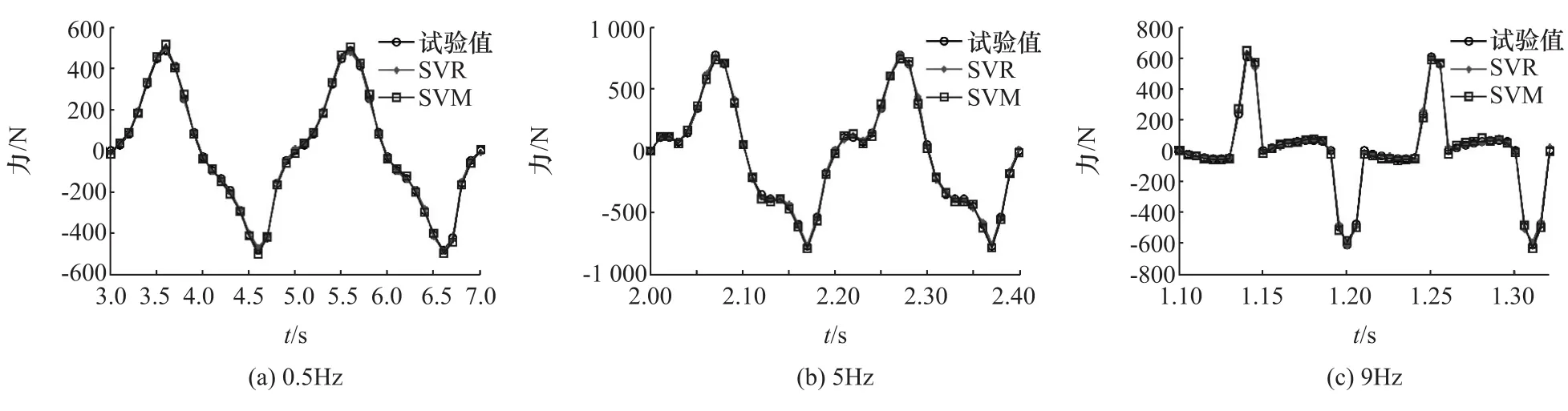
图5 力学预测

表3 预测输出参数

由图5和表3可知，回归型支持向量机(SVR)预测模型相对传统的支持向量机(SVM)模型预测精度明显提升。其中当激振频率为0.5Hz时，回归型支持向量机的均方误差E和决定系数R2分别为0.001 46和99.38%，与支持向量机的0.004 714和96.29%相比，预测精度明显提升，其中均方误差对比降幅为69.03%；当激振频率为5Hz时，SVR的均方误差从SVM的0.003 673降低到0.000 873，降幅76.23%，而决定系数从 96.89%提升到了99.48%；当激振频率为9Hz时，SVR的均方误差下降了63.18%，决定系数从96.56%提升至98.93%。

5 结论

(1)互联液压缸存在复杂的非线性因素和力学耦合效应，对其力学特性影响明显，通过力学性能试验可有效揭示非线性因素对互联液压缸力学性能影响机理。

(2)互联液压缸力学特性受非线性影响呈现多变特征，利用回归型支持向量机构建的力学性能预测模型对试验数据进行训练，可以对互联液压缸输出力进行准确预测，且相对支持性向量机预测精度明显提升。

[1] National Highway Traffic Safety Administration.Traffic safety facts[R].2004.

[2] 耶尔森·赖姆帕尔.汽车悬架[M].2版.李旭东，译.北京:机械工业出版社，2013.

[3] 徐志生.汽车理论[M].5版.北京:机械工业出版社，2011.

[4] HAWLEY J B.Shock absorber and the like for vehicles:US 1647518[P].1927-11-01.

[5] MONLTON A E，BEST A.Rubber springs and interconnected suspension systems[C].Proceedings of Engineering Design Show Conference，1970，15a.

[6] LIU P J， RAKHEJA S， AHMED A K W.Properties of an interconnected hydropneumatic suspension system[J].Transactions of the Candian Society for Mechanical Engineering，1995，19:383-396.

[7] LIU P J， RAKHEJA S， AHMED A K W.An analytical study of an interconnected vehicle suspension[C].Proceedings of ASME International Mechanical Engineering Congress and Exposition，San Francisco， CA，1995.

[8] MACE N.Analysis and synthesis of passive interconnected vehicle suspensions[D].Cambridge:University of Cambridge，2004.

[9] SMITH M C.Synthesis of mechanical networks:the inerter[J].IEEE Transactions on Automatic Control，2002，47(10):1648-1662.

[10] SMITH M C，WALKER G W.Interconnected vehicle suspension[J].Proceedings of the Institution of Mechanical Engineers，Part D:Journal of Automobile Engineering，2005，219(3):295-307.

[11] SMITH W A.An investigation into the dynamics of vehicles with hydraulically interconnected suspensions[D].Sydney:Faculty of Engineering and Information Technology University of Technology，2009.

[12] ZHUSZ，DU H P，ZHANGN.Development and implementation of fuzzy，fuzzy PID and LQR controllers for an roll-plane active hydraulically interconnected suspension[C].Proceedings of the 2014 IEEE International Conference on Fuzzy Systems，2014，1:2017-2024.

[13] LAM Q，WANGL F，ZHANGN.Experimental implementation of a fuzzy controller for an active hydraulically interconnected suspension on a sport utility vehicle[C].Proceedings of 2013 IEEE Intelligent Vehicles Symposium， Gold Coast，2013，4:383-390.

[14] SHAO X X，ZHANG N.Fuzzy control of hydraulically interconnected suspension with configuration switching[C].Proceedings of the Vehicular Electronics and Safety， Guangdong，2013，1:66-71.

[15] ZHANG N，SMITH W A，JEYAUMARAN J.Hydraulically interconnected vehicle suspension:background and modelling[J].Vehicle System Dynamics:International Journal of Vehicle Mechanics and Mobility，2010，48(1):17-40.

[16] 方志刚.汽车液电馈能式减震器馈能理论及阻尼特性研究[D].武汉:武汉理工大学，2013.

[17] 汪若尘，吴涛，孟祥鹏，等.液压互联消扭悬架系统研究[J].农业机械学报，2015，46(2):288-293.

[18] 丁飞.重型商用车液压互联悬架系统特性分析与设计[D].长沙:湖南大学，2013.

[19] 邹游，喻凡，孙涛.非线性油气悬架的平顺性仿真研究[J].计算机仿真，2004，21(10):157-160.

[20] 李占芳，仝军令，李威.单气室油气弹簧的优化设计研究[J].振动与冲击，2011，30(4):166-172.

[21] 李海生.支持向量机回归算法与应用研究[D].广州:华南理工大学，2005.

[22] 陈果，周伽.小样本数据的支持向量机回归模型参数及预测区间研究[J].计量学报，2008，29(1):92-96.

[23] 孙德山.支持向量机分类与回归方法研究[D].长沙:中南大学，2004.

[24] 刘广东.基于支持向量机的地面驱动螺杆泵井工况诊断技术[J].排灌机械工程学报，2014，32(2):125-129.

[25] 刘学艺，李平，郜传厚.极限学习机的快速留一交叉验证算法[J].上海交通大学学报，2011，45(8):1140-1145.

Mechanical Performance Prediction of Interconnected Hydraulic Cylinder Based on Support Vector Regression

Wang Ruochen，Ye Qing，Ding Yanshu，Yu Feng＆ Chen Long
Institute of Automobile and Traffic Engineering， Jiangsu University， Zhenjiang 212013

In order to further study the effects of nonlinear factors on mechanical characteristics of interconnected hydraulic cylinder(IHC)under real working conditions，a bench test for the mechanical performance of IHC is carried out and the effects of nonlinear factors on its mechanical output are analyzed.In view of that traditional math model can not accurately reflect the mechanical characteristics of IHC and for reducing the data regression fitting error with traditional support vector machine(SVM)algorithm，insensitive loss function is introduced to construct a regression SVM prediction model for the mechanical performance of IHC and conduct a prediction with its results compared with test data.The results show that regression SVM prediction model has higher prediction accuracy，providing a novel research thinking for revealing the mechanical characteristics of interconnected suspension.

10.19562/j.chinasae.qcgc.2017.09.018

∗国家重点联合基金(U1564201)、江苏省自然科学基金(15KJA460005)和镇江市重点研发项目(GY2015029)资助。

原稿收到日期为2016年9月2日，修改稿收到日期为2016年11月15日。

汪若尘，教授，博士生导师，E-mail:wrc＠ujs.edu.cn。