危险换道驾驶行为预测方法研究∗

熊晓夏，陈 龙，梁 军，蔡英凤，江浩斌，陈月霞

危险换道驾驶行为预测方法研究∗

熊晓夏，陈 龙，梁 军，蔡英凤，江浩斌，陈月霞

(江苏大学汽车与交通工程学院，镇江 212013)

提出了两种危险换道驾驶行为预测算法，分别为基于贝叶斯因子阈值法的隐马尔可夫模型预测算法和基于运动时间窗特征提取法的支持向量机预测算法，它们所需的车辆运行特征变量均可在车联网环境下获得。通过基于Prescan-Simulink联合仿真的驾驶员在环仿真，获得危险和正常两种换道场景下的车辆运动数据，进而对提出的两种算法进行验证和比较。结果表明，两种预测算法对危险换道驾驶行为的预测均有较高的准确率，有助于对危险换道的驾驶员给予及时警告或辅助纠正，从而减少危险换道事故的发生。在样本数据有限的条件下，SVM算法的预测效果更好。

换道预警；行为预测；隐马尔可夫模型；支持向量机

Keywords:lane change warning；behavior prediction；HMM；SVM

前言

换道是驾驶过程中最常见同时也是危险程度较高的驾驶行为。根据美国高速公路安全管理局(NHTSA)研究数据表明，由于换道过程引发的交通事故在所有统计的交通事故中占比高达27%[1]。在对本车和周围车辆运行状态感知的基础上，研究危险换道驾驶行为的预测方法，有助于实现辅助驾驶系统准确、及时地换道预警或干预。

现有的大量换道预警研究均是以基于车速和相对距离的碰撞时间(time to collision，TTC)[2-3]或基于车辆制动运动学分析的最小安全车距(minimum safe spacing，MSS)[4-5]作为预警参数，通过确定预警参数的阈值建立不同的预警策略。而实际上，危险换道从换道开始到发生危险冲突的整个过程很难用单一的预警参数进行描述，需要采用更复杂的算法和模型进行研究。为此，本文中选取了机器学习中生成模型和判别模型的典型代表隐马尔可夫模型(hidden Markov model，HMM)和支持向量机(support vector machine，SVM)两种模型算法，建立了基于两种算法的危险换道驾驶行为预测模型。目前，HMM和SVM已在驾驶员意图/行为(如直行、转向、变换车道等)识别方面取得了良好的预测效果并广泛应用于车辆辅助驾驶系统中[6-7]，但在换道驾驶行为危险性预测方面研究较少[8-9]。文献[8]中基于换道后果将换道行为划分为危险换道和正常换道，并通过观测换道前1s车辆运动数据应用HMM对换道后果进行分类预测。文献[9]中通过聚类分析将车辆换道对目标车道后车的影响划分为危险、安全和舒适3个等级，并应用SVM对换道影响进行分类预测。然而以上研究均是对HMM和SVM进行初步探索应用，没有对预测模型的具体构建方法(如模型判定的选择和学习数据的构建等)进行深入研究，获得的预测效果十分有限，且均未对两种方法进行对比分析。

因此，本文中主要从如下几方面展开研究:首先，对危险换道驾驶行为预测问题进行阐述分析；其次，具体分析机器学习中的生成模型算法HMM和判别模型算法SVM两类模型算法，并针对危险换道驾驶问题提出基于两种算法的预测模型；最后通过基于Prescan-Simulink联合仿真的驾驶员在环仿真平台获取换道场景数据对提出的算法进行检验和比较。

1 问题描述

本文中主要通过研究模型算法来预测驾驶员换道行为是否为危险换道行为。定义的危险换道行为包括两种情况:(1)最终导致碰撞事故；(2)未导致碰撞事故但驾驶员采取了紧急避让措施(如猛打转向盘或紧急制动)(这是因为采取紧急避让措施虽然避免了碰撞事故的发生，但该驾驶行为本身危险性很高，极易引发人身安全事故，故应归为危险换道行为的类别)。预测模型算法应同时满足快速性和准确性两方面的要求。

(1)快速性

快速性是指从车辆采取换道行为开始，能够在尽可能短的时间区间内对该换道驾驶行为做出危险性预测。为了在发生危险冲突前实现危险换道驾驶行为预警(换道预警系统的及时性需求)，选择从车辆开始发生持续换道横向位移时刻t0(定义为换道过程的起点[10])至车辆越过相邻车道线(车身越线)时刻tw作为模型的预测区间，如图1所示。

图1 预测区间运动时间窗

(2)准确性

准确性是指在一定的时间区间内做出的危险性预测的正确性能尽量满足驾驶员安全驾驶的要求。本文中拟采用信号检测理论(signal detection theory，SDT)框架[11]对预测模型的准确性进行评价，其中预测结果可按实际结果分为4类，如表1所示。对于危险换道驾驶预测问题，通常需考虑驾驶员对预测结果为FP(实际为正常换道但被预测为危险换道)的容忍限度，在实际应用中通常选为5%。因此，在模型训练阶段，需保证在预测结果FP比率低于5%的情况下，通过调整模型参数尽量使预测结果TP(正确地被预测为危险换道)比率达到最大值。

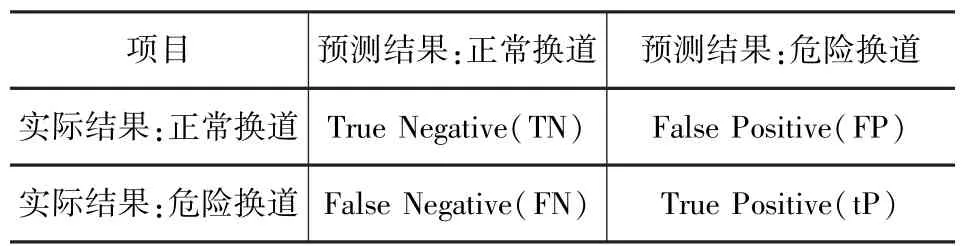
表1 预测结果划分

2 预测模型

本文中危险换道驾驶行为预测是基于预测区间[t0，tw]内车辆的实时运行数据(时间序列数据)完成的。在运用HMM和SVM模型算法进行预测之前，首先需要获取预测区间内的观测样本(即训练集)对预测模型进行训练，且为实现预测模型对正常换道驾驶行为和危险换道驾驶行为的划分，训练集中的观测样本亦被划分为危险驾驶样本集和正常驾驶样本集两类。具体的观测样本获取方法将在第3节详细阐述。

2.1 基于HMM算法的危险换道驾驶行为预测模型

HMM作为机器学习中生成模型的代表之一，其思想为首先建立样本的概率密度模型，然后再利用模型进行推理预测。HMM对观测事件的概率建模基于如下假设[12]:可观测的事件由一系列有限的不可观测的隐含状态决定(输出)并符合一般随机过程，而隐含状态之间的相互转换过程符合马尔可夫随机过程，即双重随机过程假设。考虑到车辆运行数据为连续型，而高斯混合模型GMM可以无限逼近任意连续型变量的分布，故采用GMM建立状态输出事件的随机分布函数。基于GMM描述输出的HMM 模型可表述为 λ ＝{Π，A，c，μ，U}， 其中关键概念和参数含义如下[12]。

(1)隐含状态序列:即与一个观测样本观测值序列相对应的不可观测的隐含状态序列Q＝q1，q2，…，qT，其中每一个隐含状态qt来自于包含N个状态的有限集合S，S＝{s1，s2，…，sN}。

(2)观测样本观测值序列:即在预测区间[t0，tw]内可直接观测得到的一个观测样本的观测值序列O ＝ o1，o2， …，oT， 其中每一个观测值ot∈Rd是t时刻观测得到的d维车辆运行特征向量(如车辆的运行速度和位置变量等)。

(3)状态转移概率:aij，i，j＝ {1，2，…，N}，代表了系统由状态Si转移至Sj的概率，不同状态间的转移概率即构成状态转移矩阵A。

(4)状态输出事件的随机分布函数:

式中:N(μjm，Ujm)为状态j下输出值的多维高斯密度函数，其中μjm为均值向量，Ujm为协方差矩阵；M为高斯混合数目；cjm为高斯混合系数(或权重)以确保(5)初始状态分布:ΠT＝ [π1，π2，…，πN]，其中πi代表初始隐含状态为Si的概率。

本文中采用EM(expectation-maximization)算法(在HMM模型学习中亦被称为Baum-Welch算法)对HMM模型λ进行学习从而获得λ参数的最大似然估计，具体算法形式可参见文献[12]。由于EM算法只能保证获得局部最优解，因此参数的初始值选择尤为重要。以往研究表明，Π和A的初始值选取对HMM模型训练最后的收敛结果影响较小，因此可在满足马尔可夫链的条件下采用随机或均匀取值对其初始化；而c，μ和U的初始值选取对最后结果影响较大，需要采用更为复杂的初始化方法[6]。故本文中采用K-means聚类算法按照状态数N和高斯混合数M将观测样本序列自动聚为N×M类并得到c，μ和U的初始值。若记状态n内的第m个高斯元所代表的类为lnm，则可根据观测样本{oi}，i＝1，2，…，nsample(共nsample个观测向量数)计算c，μ和U的初始值:

式中:x为观测向量；l为某一聚类类别。

在分别学习并获得正常驾驶HMM模型λ0和危险驾驶HMM模型λ1基础上，给定任意一组新的观测值序列z，则可通过forward算法[12]分别计算正常驾驶下和危险驾驶下观测值的似然值P(z｜λ0)和P(z｜λ1)。为了提高模型的预测精度，采用贝叶斯模型选择方法计算比较两个模型的贝叶斯因子[13]，并对其进行阈值分析获得最后的驾驶行为分类。根据贝叶斯定理，已知观测值的模型后验概率P(λi｜z)满足:

则两个模型的贝叶斯因子BF满足:

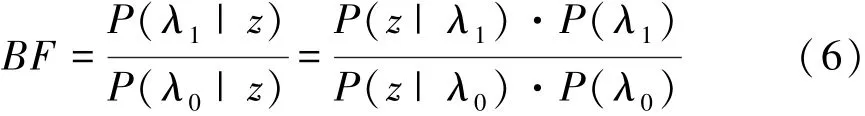
由于对该驾驶员是否会危险驾驶不具备先验知识，故先验概率 P(λ1)＝P(λ0)＝ 0.5，故式(6)可化简为

因此，可为贝叶斯因子BF设置阈值eτH(考虑通常使用log-likelihood计算BF值，故在阈值中加入指数项e方便计算)，当BF ＞eτH时，判定该观测值为危险驾驶行为。阈值eτH的选择可以反映HMM预测模型的保守性，即eτH越大，判别结果为危险驾驶的可能性越低，该预测模型表现则越保守(FP的可能性降低)。

综上，基于HMM的预测流程如图2所示，其中虚线所示部分为模型训练阶段，实线所示部分为模型预测阶段。

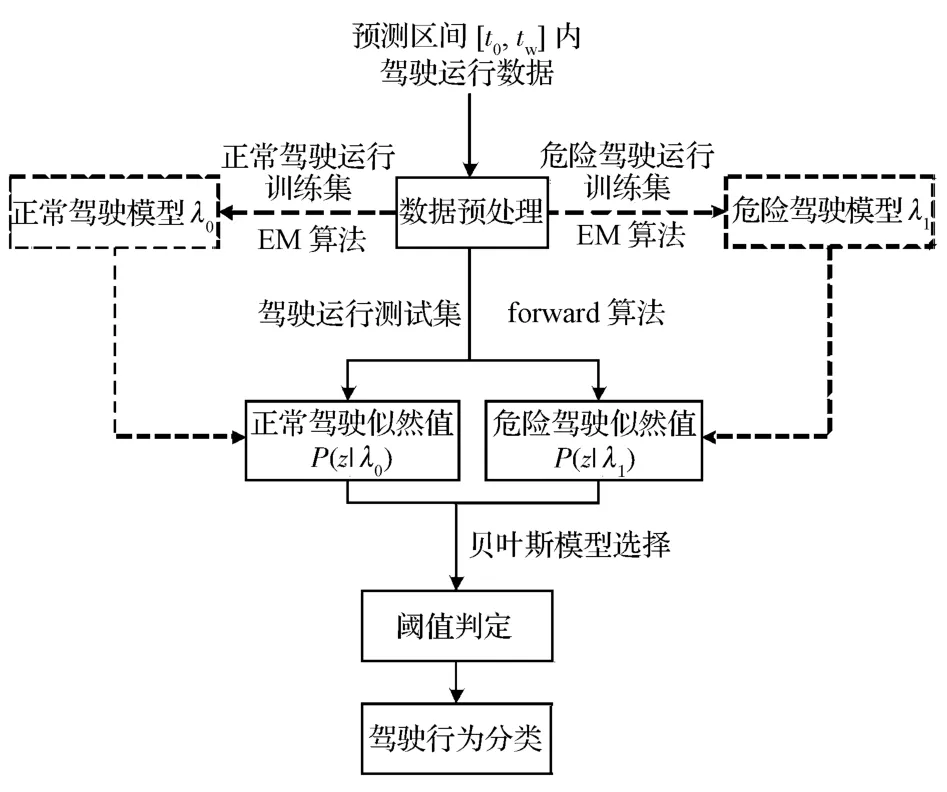
图2 基于HMM的驾驶员换道行为系统预测流程图

2.2 基于SVM算法的危险换道驾驶行为预测模型

SVM为机器学习中判别模型的代表之一，其不考虑样本的产生模型，而是直接建立判别函数作为预测模型。不同于HMM本身即为时间序列数据模型，SVM对输入值为时间序列的数据进行分类时首先需要对原始数据进行数据降维。假设xi∈Rd为预测区间[t0，tw]内通过数据降维(特征提取)得到的一组d维车辆运行特征向量，若给定N组带标记的训练数据{xi，yi}，i＝ 1，2，…，N，则可通过学习训练直接建立如下判别函数D(z)[14]来判定新的观测向量z所属的类别:

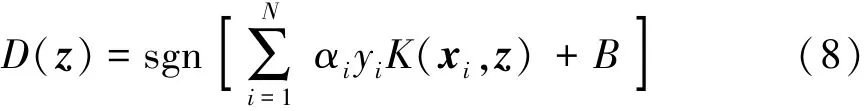
式中:与每组特征向量xi相对应的危险驾驶行为判别值由yi∈{+1，-1}表示，其中 +1代表危险驾驶类别，-1代表正常驾驶类别；K(xi，xj)指核函数，即将原始向量xi和xj投影至特征空间后作内积；B为偏差因子项；α为系数向量。α的取值需满足约束要求并同时使如下表达式W(α)达到最大值[14]，即

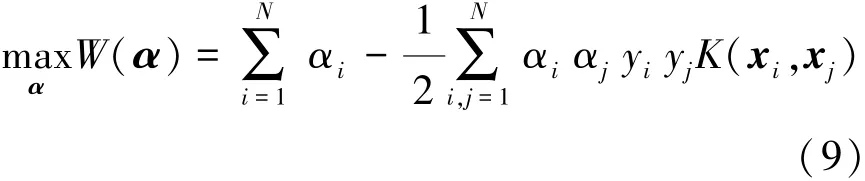
由此可得，基于SVM的预测模型精度主要受核函数K(xi，xj)的选择和特征向量x的提取两方面影响。因此，在实际模型训练阶段需选取不同的核函数和特征变量组合进行试验，并选定具有最优预测效果的核函数和特征变量组合进行危险换道驾驶行为预测。

为有效反映原始数据中的时间依赖性信息进而提高模型的预测精度，本文中建立了基于运动时间窗的换道驾驶行为特征提取方法，如图1所示。首先将预测区间[t0，tw]按时间窗长度Step和运动间隔Interv划分为不同的运动时间窗 SW1，SW2，…，SWk，…，SWK，然后对每个运动时间窗内的时间序列数据进行特征提取(如提取SWk内车辆运行速度的均值和方差等作为该运动时间窗的特征向量xk)得到K个d维车辆运行特征向量 x{1，x2，…，xk，…，xK}，最后采用权重系数法获取整个预测区间的车辆运行特征向量其中wk为运动时间窗 SWk的权重。

考虑到靠近预测节点tw的时间窗与之前的时间窗相比应赋予更大的权重(最新的运动状态数据较之前数据更接近危险发生状态故更能反映驾驶行为的危险性)，故采用基于时间距离的指数型折减系数函数dk来计算各个时间窗的权重wk:

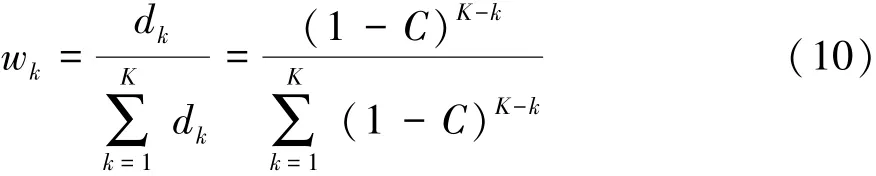
式中 C∈[0，1)为折减系数常数，且 d1＝(1-C)K-1≤1，dK＝1，故dk的含义为距离时间窗 SWK越远(k→1)，则该时间窗内特征值被折减的值越大，其在所有时间窗内所占权重wk越小。注意，当C＝0时等同于每个时间窗的权重相等(即特征值均无折减的情况)。

综上，基于SVM的预测流程如图3所示。

图3 基于SVM的驾驶员换道行为系统预测流程图

3 仿真检验

3.1 数据来源

由于交通事故为小概率事件，故在实际工程中较难获取满足研究需要的大量真实事故数据，特别是针对某一类事故场景的数据(如本文中换道驾驶场景事故数据)。因此，许多学者通过仿真不同的危险场景进行交通事故相关研究[15-18]，仿真中危险场景的形成可以是由于人的因素(如超速驾驶和分心驾驶[15])、环境的因素(如交通流量的变化和道路几何线形的变化[16])或是突发事件(如突然闯入道路的行人[17]或突然驶入交叉路口的车辆[18])等。相似地，本文中通过设计危险换道和正常换道仿真场景，利用基于Prescan-Simulink联合仿真和罗技驾驶模拟器的驾驶员在环半实物仿真平台，获取了危险场景和正常场景的车辆运动数据对前文提出的算法进行校验。仿真过程中，Prescan软件平台主要负责构建仿真基本场景(如道路设施、交通设施和天气情况等)，Simulink主要提供仿真交通控制模块(如周围车辆的运行状态)，而驾驶员则需通过驾驶模拟器控制本车(研究车辆)在Prescan-Simulink联合构建的仿真交通场景中完成换道驾驶任务。

本文中设计的危险和正常换道场景发生在典型的超车场景，即在天气状况良好的双车道高速公路直线段上，研究车辆在外车道由后方逐渐驶近前车车辆1，并试图换道至内车道进行超车(此时超车道上有车辆2正在前方行驶)，如图4所示。若此时超车道上前车车辆2突然减速(可能由于某种突发事件，如路面突然出现障碍物等)，则出现危险换道场景；若超车道上前车车辆2继续保持之前正常运行状态，则为正常换道场景。因此，本文中仿真试验主要研究在换道过程中本车(研究车辆)与超车道上前方车辆2之间的危险冲突。

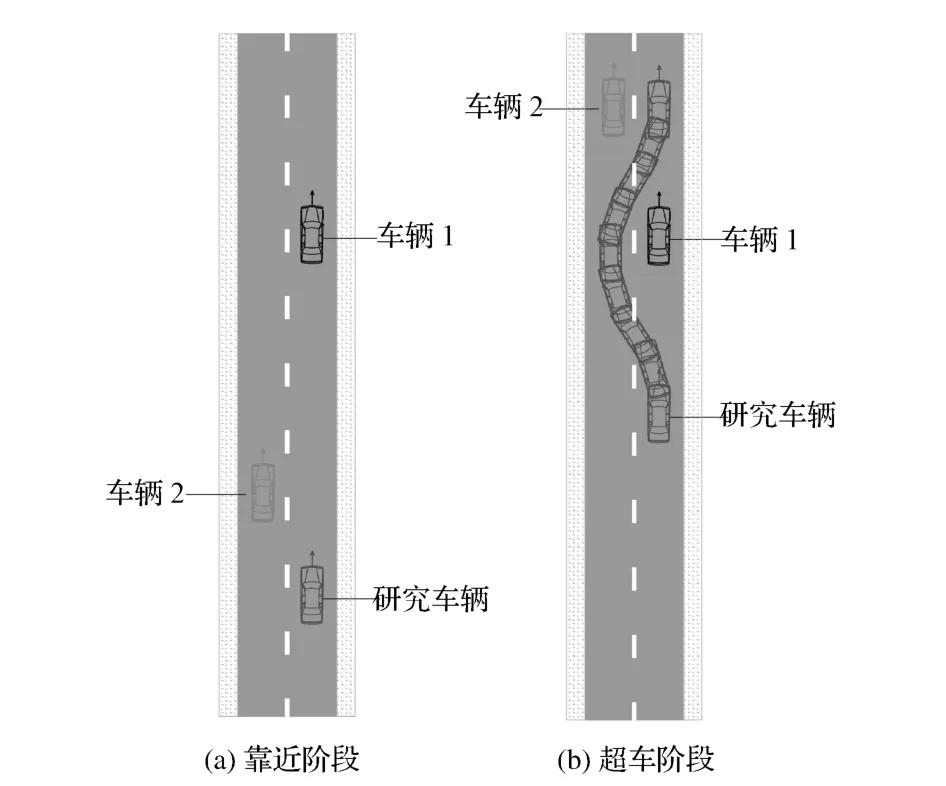
图4 仿真场景示意图

仿真试验共选取20名1年以上驾龄的驾驶员(10名男性和10名女性，年龄22～25岁)，其中每名驾驶员被要求完成20次不同场景的换道试验。在仿真过程中，驾驶员的反应行为不受任何限制，即驾驶员可在任一时刻根据对不同场景的主观判断作出不同反应，如制动或避让行为。为了使仿真过程中驾驶员的行为反应更接近于真实状态(避免由于多次相同试验而形成机械式驾驶行为)，仿真试验按研究车辆与车辆1初始相对碰撞时间T的不同划分为不同场景(如表2所示)并随机安排给驾驶员，同时随机分配危险换道场景(车辆2突然减速)和正常换道场景(车辆2正常行驶)(两种场景各占50%)。其中初始相对碰撞时间T的定义为:研究车辆在指定点达到指令规定的初始速度后(相应地将此指定点定义为仿真场景中研究车辆的初始位置，与其对应的时间节点定义为仿真场景的初始时刻)，若继续保持匀速向前行驶(不采取任何加减速行为)，则其与前车车辆1发生碰撞所需的行驶时间为初始相对碰撞时间T。表2所示不同仿真试验的关键参数T，D01和 D21应满足:

式中:V0，V1和V2分别为仿真试验中研究车辆的初始速度，车辆1的运行速度和车辆2的运行速度；D01为研究车辆至车辆1的初始距离，取值大小由试验随机指定(为实现不同仿真场景)；t为由初始时刻至驾驶员准备换道的时长；C21为驾驶员准备换道时车辆2相对于车辆1的纵向距离(同时假设危险换道场景中车辆2在该位置突然开始减速)；C01为此时研究车辆相对于车辆1的纵向距离(假设研究车辆在换道前按初始速度匀速行驶)；D21为车辆2至车辆1的初始距离。由于C21的值将直接影响危险场景能否有效实现，而C01的值随不同驾驶员行为习惯的不同(如换道时机选择的不同)将有所变化，因此，本文中进行了不同仿真场景的预试验来确定该两个场景参数的设计值(以尽可能自然地实现危险换道和正常换道场景)，从而获得参数D21的设计值，如表2所示。

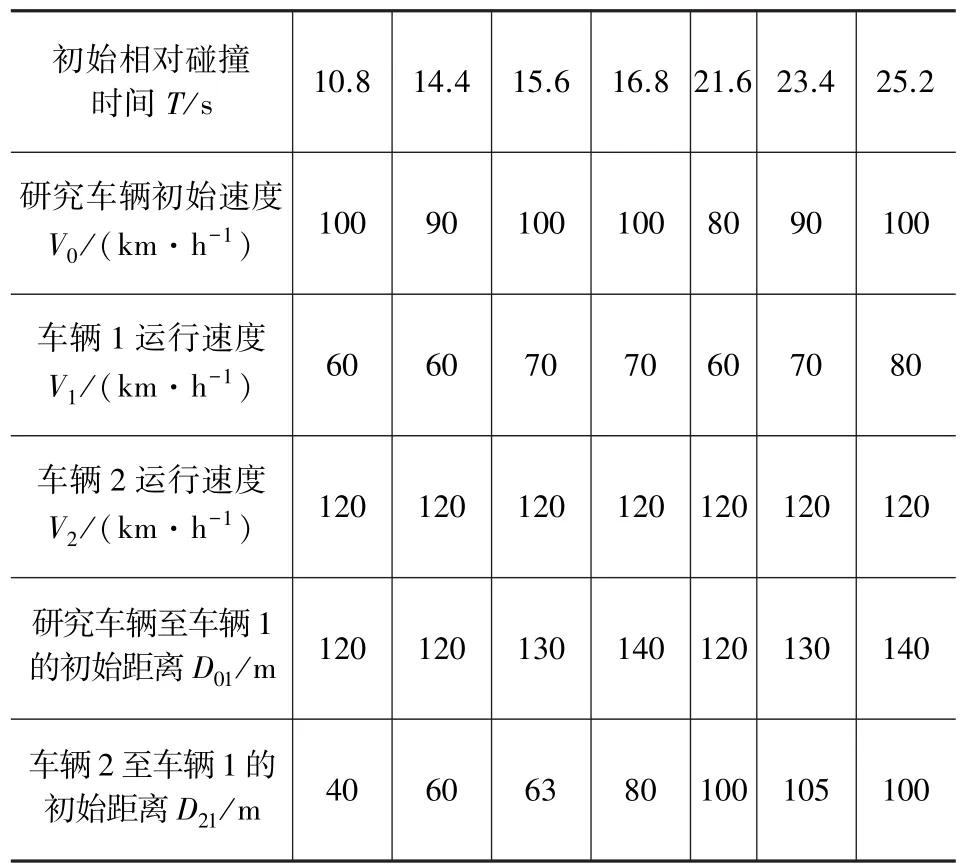
表2 仿真试验关键参数

以上设计的车辆1和2的运行轨迹和运行速度等参数均可在Prescan-Simulink联合仿真平台中设定，从而为驾驶仿真试验提供不同的仿真场景。

仿真试验过程采集了驾驶员驾驶车辆(研究车辆)和超车道前方车辆2的运行特征时间序列数据(采样频率为10Hz或0.1s)，具体变量包括车辆质心位置、横摆角速度、航向角、纵/横向速度、纵/横向加速度。仿真试验最终获得符合要求的危险场景样本数据198组，正常场景样本数据200组，其中75%的数据作为模型训练样本，剩余25%的数据作为模型测试样本。利用 Matlab工具箱[19-20]分别对基于HMM和SVM的预测模型进行训练。

3.2 基于HMM的预测模型结果

通过选取不同的特征变量组合进行试验，最终选取运行特征向量o＝{两车横向、纵向速度差，两车横向、纵向加速度差，两车运行方向夹角，两车质心距离}进行模型训练和预测，其中各变量数据均经过归一化处理以消除不同数据的量纲影响。由2.1节可得，HMM预测模型关键参数包括:(1)状态数N(正常N0，危险N1)；(2)高斯混合数M(正常M0，危险M1)；(3)阈值常数τH。考虑到过高的N和M值将增大模型的复杂程度且容易造成过拟合问题，因此模型仅考虑N和M在2～15范围内取值。采用十折交叉验证法对模型进行训练(基于训练样本)，在保证预测结果FP值低于5%的情况下，利用网格搜索法获得使TP比率值(%)最大的前10个参数取值，组合如表3所示。

表3 HMM预测模型5%FP下最优TP值参数组合

由表3可见，总体上危险换道驾驶的隐含状态数N和高斯混合数M均比正常换道驾驶多，说明相对于正常换道驾驶而言，危险换道驾驶车辆运行数据间差异性更大(更多状态划分)且分布特性更复杂(每个状态下更多高斯混合)。该结果较符合人们的一般期望，即危险换道行为的生成机理比正常换道行为具有更多的不确定性和复杂性。另外，试验显示τH＝0时(即选取贝叶斯因子BF＞1作为模型λ判别依据)预测TP值仅为78.3%，表明提出的贝叶斯因子阈值法有利于提高HMM的预测精度。

最后，选取表3中最优参数组合1对测试样本进行预测，预测结果的TP和FP值分别为81.5%和4.5%，基本满足危险换道预警的要求。

3.3 基于SVM的预测模型结果

通过选取不同的核函数和特征变量组合进行试验，最终选定径向核函数为预测危险换道驾驶问题的最优核函数，选取时间窗特征向量xk＝{两车横向、纵向速度差平均值，两车横向、纵向速度差方差，两车质心距离平均值，两车质心距离方差}进行模型训练和预测。由2.2节可得，SVM预测模型关键参数包括:(1)运动时间窗长度Step(S)；(2)运动时间窗间隔Interv(I)；(3)权重折减系数常数C。采用十折交叉验证法对模型进行训练(基于训练样本)，在保证预测结果FP值低于5%的情况下，利用网格搜索法获得使TP比率值(%)最大的前10个参数取值组合，如表4所示。

表4 SVM预测模型5%FP下最优TP值参数组合

由表4可见，当运动时间窗时长和运动间隔时间同时增大时，为了达到较好的预测效果(较高的TP值)，权重折减系数总体上趋向于0。该结果表明，当每个窗体的长度增加且窗体间不重合的区间增大时，即预测区间内划分的窗体个数K减少时，缩小窗体之间对预测贡献比例的差别(由2.2节可知C＝0代表每个时间窗的权重相等)将有利于获得较高的预测准确率。同时，本文中亦对未划分时间窗的情况(即Step＝[t0，tw])进行了对比试验，结果显示其预测TP值仅为86.3%，表明提出的基于运动时间窗的特征提取方法有利于提高SVM的预测精度。

最后，选取表4中最优参数组合1对测试样本进行预测，预测结果的TP和FP值分别为88.7%和4.0%，基本满足危险换道预警的要求。

3.4 预测模型预测性能比较分析

以上结果表明，根据目前有限的仿真试验样本数据，本文中建立的HMM和SVM模型的泛化能力均较强，且在5%FP条件下均已达到了80%以上的TP准确率，可以基本满足危险换道预警的要求。由于仿真试验获得的数据难以完全真实地反映驾驶员的实际操作行为特征进而可能影响模型分类预测的效果[9]，因此从工程应用方面考虑，未来仍需获取更多真实的危险场景换道驾驶数据(如自然驾驶数据)对HMM和SVM模型进行训练并进一步提高模型的预测准确率。

另外，两个模型相比较而言，在目前仿真试验样本条件下HMM的预测效果不如SVM。其中的原因可能是HMM需要基于两类样本数据利用最大似然法分别拟合两个生成模型，而最大似然估计对样本数据中可能包含的少量离群数据鲁棒性不强[13]；相反，SVM只需寻找两类样本数据的分类边界或分类超平面，故对样本数据的要求较HMM要低，更适合在目前危险换道场景样本数据有限的情况下使用。未来在获得更多危险场景换道驾驶数据的条件下两者相对预测性能的变化将值得进一步研究。

4 结论

本文中针对危险换道驾驶问题提出了基于贝叶斯因子阈值法的HMM和基于运动时间窗特征提取法的SVM两种预测算法，并通过驾驶员在环半实物仿真平台采集的不同换道场景数据对预测算法进行了测试。结果表明，依据现有的仿真试验样本数据，通过选取合适的特征量和模型参数，两种预测算法的TP预测率均能在FP低于5%的条件下达到80%以上，基本符合换道预警的要求。未来可通过获取更多实际的危险换道驾驶数据对预测模型进行优化，并考察模型的在线实时预测效果，将其应用到安全辅助驾驶系统中。

[1] National Highway Traffic Safety Administration.National motor vehicle crash causation survey:report to congress[R].National Highw Trafc Saf Adm，2008.

[2] JULA H，KOSMATOPOULOS E，IOANNOU P.Collision avoidance analysis for lane changing and merging[J].IEEE Transactions on Vehicular Technology，2000，49(6):2295-2308.

[3] 张琼.基于驾驶人感知特性的换道预警阈值研究[D].西安:长安大学，2013.

[4] DASS， SUN X， WANG F， et al.Estimating likelihood of future crashes for crash-prone drivers[J].Journal of Traffic and Transportation Engineering(English Edition)，2015，2(3):145-157.

[5] 王畅，付锐，张琼，等.换道预警系统中参数TTC特性研究[J].中国公路学报，2015，28(8):91-107.

[6] 吕岸，胡振程，陈慧.基于高斯混合隐马尔科夫模型的高速公路超车行为辨识与分析[J].汽车工程，2010，32(7):630-634.

[7] 宗长富，王畅，何磊，等.基于双层隐式马尔科夫模型的驾驶意图辨识[J].汽车工程，2011，33(8):701-706.

[8] 倪捷，刘志强，涂孝军，等.面向驾驶辅助系统的换道安全性预测模型研究[J].交通运输系统工程与信息，2016，16(4):95-100.

[9] LIU P， KURT A，REDMILL K，et al.Classification of highway lane change behavior to detect dangerous cut-in maneuvers[C].TRB 95th Annual Meeting Compendium of Papers，2016.

[10] SALVUCCI D.Inferring driver intent:a case study in lane-change detection[J]Proc.Human Factors Ergonomics Society，2004:2228-2231.

[11] MCNICOL D.A primer of signal detection theory[M].Hillsdale，NJ， Lawrence Erlbaum，2004.

[12] RABINERL R，JUANG B H.An introduction to hidden Markov models[J].IEEE ASSP Magazine，1986，3(1):4-16.

[13] BISHOP C M.Pattern recognition and machine learning[M].New Jersey:Springer-Verlag New York， Inc.，2006.

[14] CORTESC，VAPNIK V.Support vector networks[J].Machine Learning，1995，20:273-295.

[15] PORTOULI E， PAPAKOSTOPOULOS V， NATHANAEL D.Combined effect on accident risk of a dual task and higher driving speed:a simulator study[J].EPCE/hCII，2013:36-42.

[16] BELLA F， D′AGOSTINI G.Combined effect of traffic and geometrics on rear-end collision risk:driving simulator study[J].Trans.Res.Rec.:J.of the Trans.Res.Board，2010，2165:96-103.

[17] JURECKI R S， Stańczyk T L.Driver reaction time to lateral entering pedestrian in a simulated crash traffic situation[J].Tran.Res.Part F:Traffic Psychology ＆ Behaviour，2014，27:22-36.

[18] STANCZYK T L，LOZIA，Z，PIENIAZEK W，et al.Research studies on drivers’reactions for incoming vehicle from right-hand side[C].In Proc.of the 19th Annual Congress EVU，Praque(Czech Republic)，2010:41-53.

[19] MURPHY K.Hidden Markov model(HMM)toolbox for Matlab[EB/OL].http://www.cs.ubc.ca/～murphyk/Software/HMM/hmm.html.

[20] CHANG C，LIN C.A library for support vector machines(LIBSVM)[EB/OL].http://www.csie.ntu.edu.tw/～cjlin/libsvm/.

A Study on the Driving Behavior Prediction of Dangerous Lane Change

Xiong Xiaoxia，Chen Long，Liang Jun，Cai Yingfeng，Jiang Haobin＆ Chen Yuexia
School of Automotive and Traffic Engineering， Jiangsu University， Zhenjiang 212013

Two prediction algorithms for dangerous lane change driving behavior，i.e.prediction algorithm based on hidden Markov model(HMM)with Bayes factor threshold and that based on support vector machine(SVM)with moving time window feature extraction，are proposed.All the vehicle moving feature variables both algorithms need can be easily obtained in connected vehicle environment.By driver-in-the-loop simulation based on Prescan-Simulink co-simulation，the vehicle motion data in both dangerous and normal lane change scenarios are obtained，and then two proposed algorithms are verified and compared.The results show that both prediction algorithms can achieve high accuracy rate in predicting dangerous lane change behavior，conductive to giving timely warning or auxiliary correction to driver making dangerous lane change，and hence reducing the occurrence of lane change accidents.Under the condition of limited sample data，using SVM algorithm can get better prediction results.

10.19562/j.chinasae.qcgc.2017.09.010

∗国家自然科学基金(U1564201，51108209，50875112和70972048)和江苏省普通高校研究生科研创新计划项目(KYLX160905)资助。

原稿收到日期为2016年9月23日，修改稿收到日期为2017年1月8日。

陈龙，教授，博士，E-mail:chenlong＠ ujs.edu.cn。