数模转换器毛刺对光纤陀螺相关检测的影响分析

丁江婷，潘 雄，张 辉

(1.北京航空航天大学仪器科学与光电工程学院，北京100191；2.西安现代控制技术研究所，西安710065）

数模转换器毛刺对光纤陀螺相关检测的影响分析

丁江婷1，潘 雄1，张 辉2

(1.北京航空航天大学仪器科学与光电工程学院，北京100191；2.西安现代控制技术研究所，西安710065）

数模转换器(DAC）是全数字闭环光纤陀螺反馈通道的重要部件，DAC的毛刺特性会对光纤陀螺的调制解调结果产生影响。基于DAC中值毛刺特性建立了光纤陀螺反馈回路的非理想调制方波模型，分析了调制频率与本征频率不同时DAC毛刺在干涉信号中产生的各类周期干扰信号。利用周期干扰信号的Fourier级数推导出了DAC毛刺造成调制解调误差的数学模型，仿真分析了数模转换器毛刺的宽度、高度，光纤陀螺调制频率、本征频率及放大电路的增益带宽对陀螺解调误差的影响。最后，通过开环实验验证了DAC毛刺对光纤陀螺调制解调的影响。

光纤陀螺；DAC毛刺；调制误差；调制频率；本征频率

Abstract：Digital to analog converter(DAC）is an important part of all digital closed⁃loop fiber optic gyroscope(FOG）feedback loop，DAC glitch will affect the result of modulation and demodulation of IFOG.The model of non⁃ideal modulated square wave was built according to the characteristic of mid⁃scale glitch，different conditions of interference sig⁃nal caused by DAC glitch when the modulation frequency is not equal to eigenfrequency were analyzed.The mathematical model of modulation and demodulation errors caused by DAC glitch were formulated by applying Fourier series of periodic interference signal.Furthermore，the effects of the glitch impulse，modulation frequency，eigenfrequency and amplifier gain bandwidth on the bias error of closed⁃loop FOG were analyzed by simulating，and the effect of DAC glitch on modulation and demodulation was verification through open⁃loop experiment.

Key words：fiber optic gyroscope;DAC glitch;modulation error;modulation frequency;eigenfrequency

0 引言

中高精度干涉式光纤陀螺普遍采用全数字闭环检测方案［1⁃2］，反馈回路中的数模转换器(DAC）是生成反馈调制和偏置调制的关键器件。高速闭环反馈与相对较低的输出更新率使得输出数据对闭环反馈数据有一个平均过程，降低了对DAC及其驱动运放的分辨率和线性度的要求［2］。随着光纤陀螺研究的深入和导航应用对高动态、高数据更新率的需求，DAC的器件特性，尤其是非线性，成为影响光纤陀螺性能的一个潜在误差源［3］。

DAC毛刺是指当输入数字量变化时，DAC输出端出现的尖峰脉冲［4］。毛刺的形成原因有两个，一个是DAC内部模拟开关的导通和截至时间存在差异，另一个是受分布参数的影响造成的输入馈送延迟。这些因素使得DAC在输出过渡期间的某一短暂时间内，输出端出现与输入数据无关的模拟输出。毛刺的大小与DAC的性能有关，且受DAC输入数据变化位数的影响。当输入数字量跨越DAC满量程的中值时(如16位 DAC发生从h7FFF到h8000的跨越），模拟输出将产生中值毛刺脉冲 (Midscale Glitch Impulse），中值毛刺通常被认为是幅度最大的毛刺［4］。

本文基于DAC毛刺特性及相关解调的原理，建立了DAC中值毛刺造成陀螺调制解调误差的数学模型，分析了该误差与毛刺宽度和高度、调制频率与本征频率的偏离程度等因素的关系，并结合调制频率、本征频率等影响因素，仿真计算了DAC中值毛刺对陀螺调制解调的影响。最后，对DAC中值毛刺造成的调制解调影响进行了开环实验验证。

1 DAC毛刺对光纤陀螺调制解调的影响建模

1.1 DAC毛刺建模

DAC中值毛刺的典型测试值如图 1(a）所示［5⁃6］。由于毛刺的波形比较复杂，精确描述是十分困难的，为简化问题，采用等宽三角形作为毛刺的平均近似数学描述［7］，如图1(b）所示。

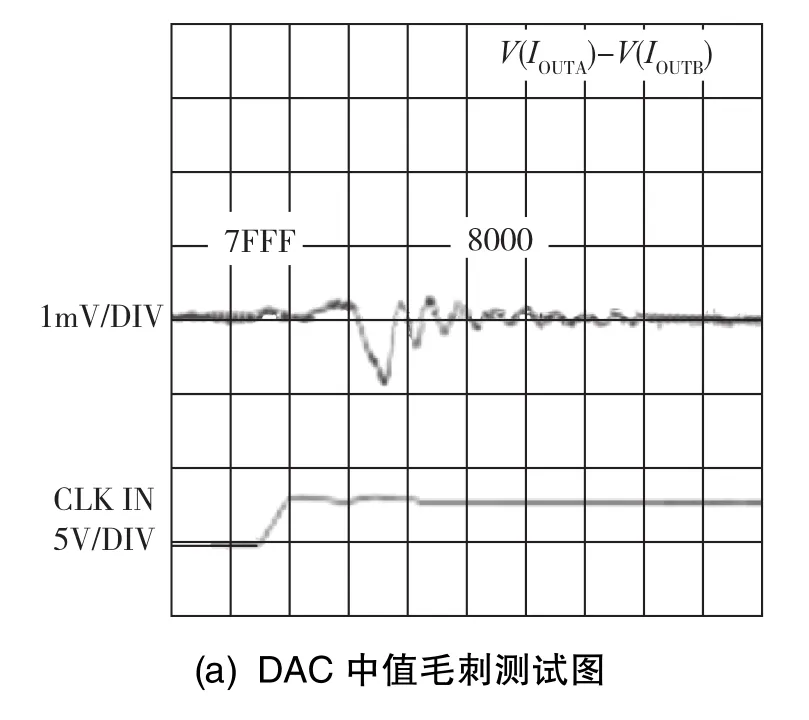
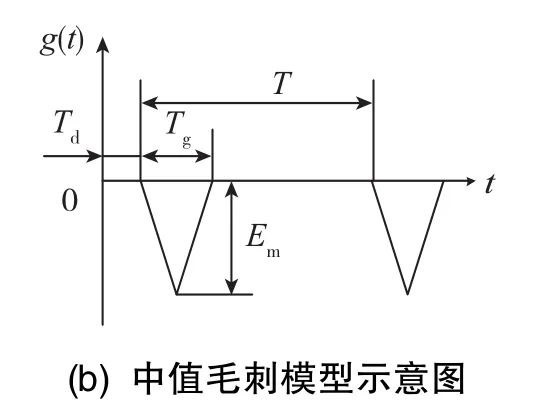
图1 DAC的中值毛刺脉冲示意图Fig.1 The schematic diagram of DAC midscale glitch

其中，Td为延迟时间，Tg为毛刺宽度，Em为毛刺幅度，毛刺表达式为：

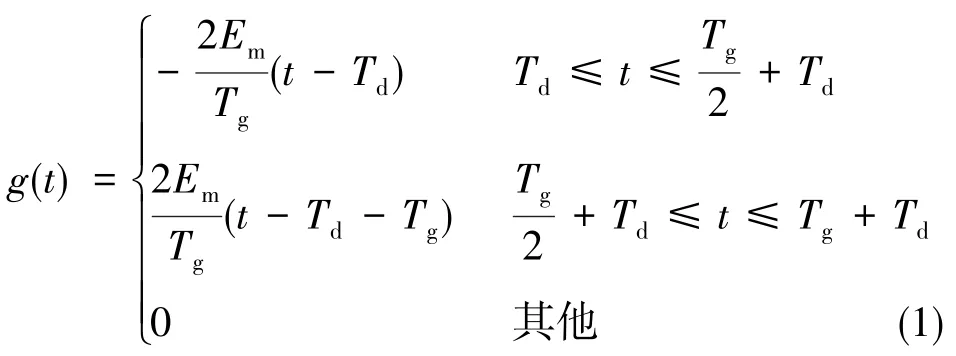
在光纤陀螺中，DAC的输出为阶梯波和调制方波的叠加，如图2(a）所示。当16位DAC的阶梯波输出在h4000～h7FFF范围内，叠加调制方波后的DAC输出跨越了h7FFF～h8000，则输出产生中值毛刺，等效于不理想调制方波与阶梯波的叠加，如图2(b）所示。

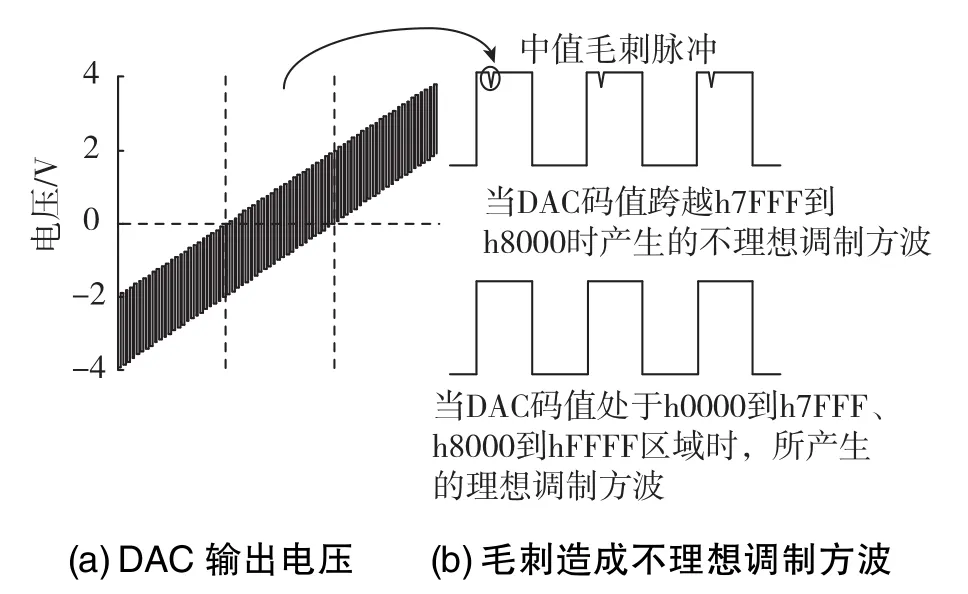
图2 DAC输出产生毛刺的范围Fig.2 The range of DAC output generated glitch

1.2 DAC毛刺对调制解调的影响分析

在图3中，Sm(t）为非理想调制方波，ϕm(t）、ϕm(t－τ）为调制相位，Δϕ(t）＝ϕm(t）－ϕm(t－τ）为干涉信号相位差，ΔP(t）为干涉信号中的脉冲干扰信号，Sr(t）为理想解调方波，Tm为调制方波、解调方波的周期。

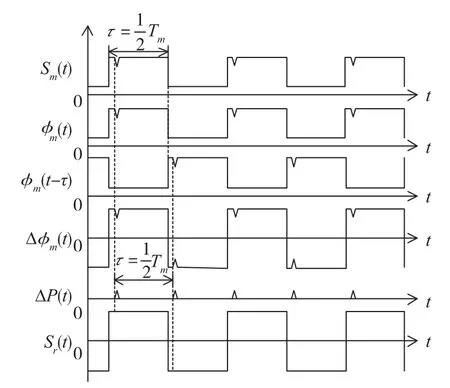
图3 fm＝fp时，DAC毛刺对调制解调的影响Fig.3 The effect of DAC glitch on modulation and demodulation whenfm＝fp

由于干扰信号ΔP(t）中的三角脉冲信号在正负半周期相应出现，相位差为π，解调方波是与调制方波同频、占空比为1∶1、幅值为±1的理想方波［8］，不考虑其他非线性效应时，干扰信号经相关解调后抵消为0。

陀螺的方波偏置调制原理如图5所示，当相位差信号Δφ在0处改变一个小角度＋Δ，正弦信号在最高处变化，灵敏度最低，干涉值I＝I0cos(0－Δ）≈I0，即可近似于常值，如图5(c）中粗线部分所示。

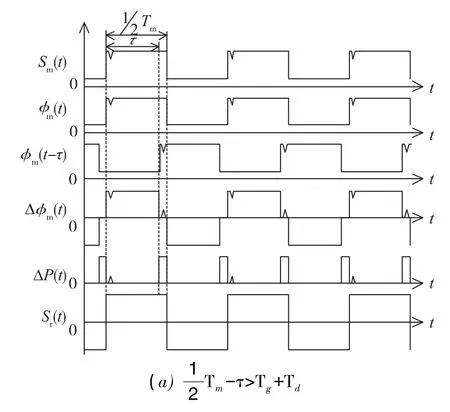
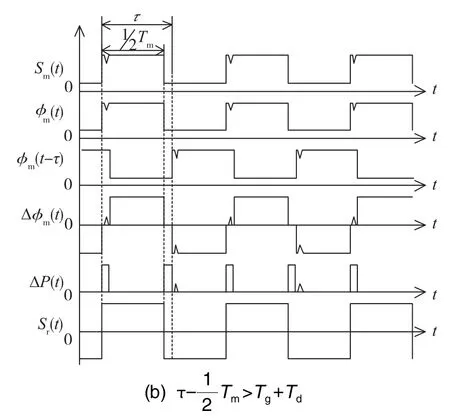
图4 fm≠fp时，DAC毛刺对调制解调的影响Fig.4 Effect of DAC glitch on modulation and demodulation whenfm≠fp

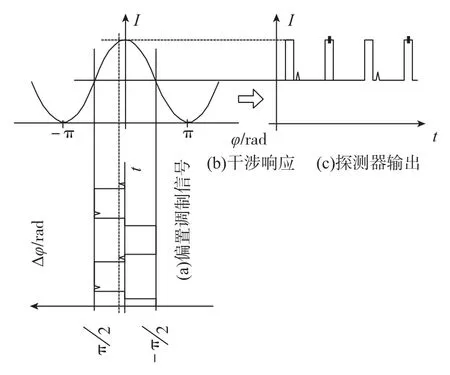
图5 相位偏置调制原理图Fig.5 The schematic diagram of square wave bias modulation

即当调制频率fm与本征频率fp不相等时，反馈回路的DAC毛刺对调制解调结果有影响。

1.3 调制解调误差的Fourier级数模型

随着陀螺调制频率fm与本征频率fp差值的改变，探测器输出的干涉信号中产生不同形式的干扰信号ΔP(t），如图6阴影部分所示。由于产生的方波脉冲误差经相关解调后抵消为0，在此不予表示，只考虑三角脉冲误差。

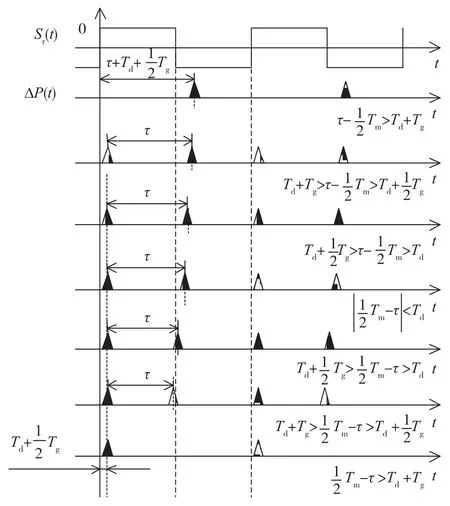
图6 fm≠fp造成干扰信号的不同形式Fig.6 Different forms of interference signal whenfm≠fp

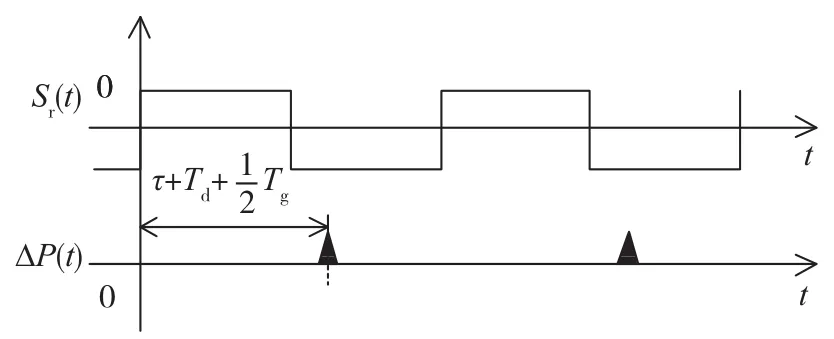
图7 时造成的干扰信号Fig.7 The interference signal when

将干涉信号中的三角脉冲干扰信号展开为Fourier级数形式：

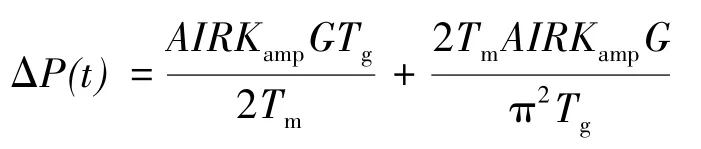
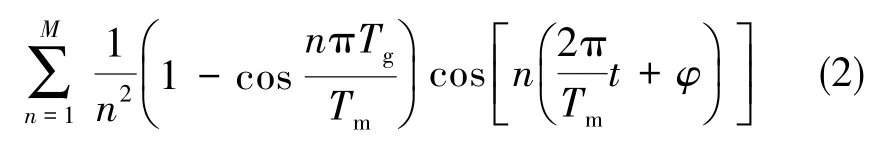
式中，I为到达探测器的光功率，AI为干涉信号中三角脉冲的高度，A为毛刺高度的比例系数；R包含探测器响应度；Kamp为前放增益，G包含AD转换器增益与数字解调增益；φ为脉冲干扰信号的相位；M为能通过信号调理电路的最高谐波次数，M/Tm表征了信号调理电路的带宽。当信号调理电路的参数确定后，其增益带宽积为有限常量c，可表示为：

闭环光纤陀螺的光电转换放大信号经过ADC转换为数字信号后到达数字信号处理(DSP）模块进行相关解调，数字闭环光纤陀螺采用数字解调方法，解调方波可认为是与调制方波同频、占空比为1∶1、幅值为±1的理想方波，其Fourier级数展开式为：

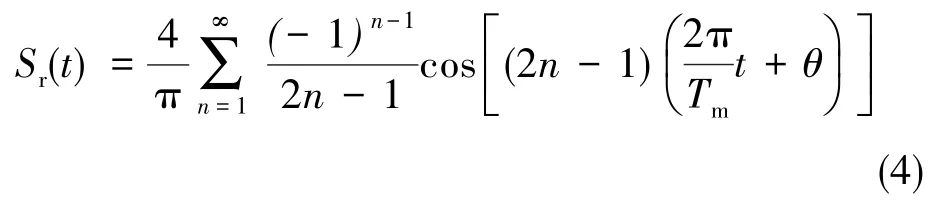
式中，θ为解调方波的相位。由于解调的本质是干涉信号与解调方波的相关，将式(2）～式(4）结合，得：

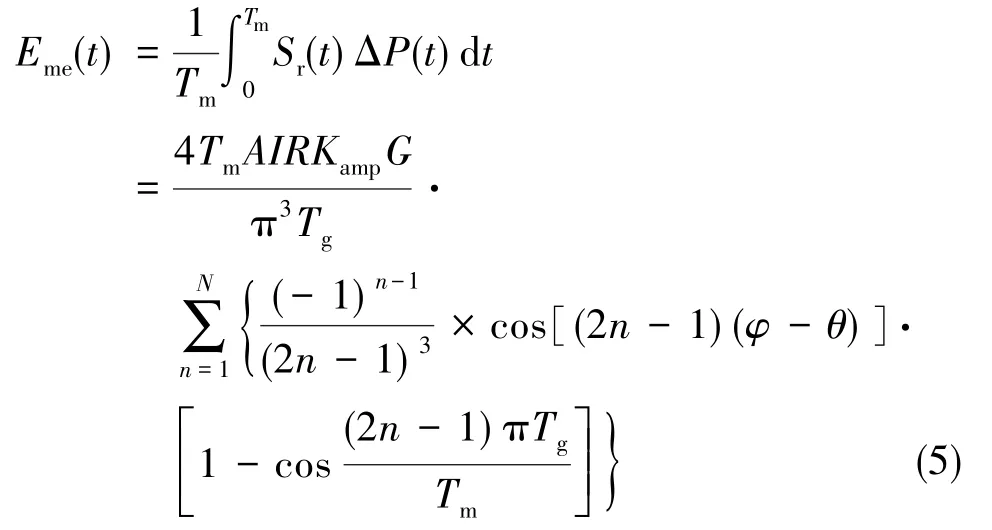
式中，Eme为DAC输出毛刺经相关解调后造成的误差；N可表示为：

在图7所示情况中，有：

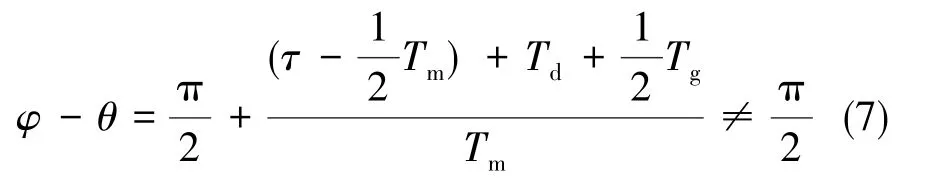
其他情况同理。当fm≠fp时，DAC输出毛刺经相关解调后造成的误差项不可能为0。

2 DAC毛刺对光纤陀螺调制解调影响的仿真结果与分析

由式(3）、式(5）和式(6）可知，DAC毛刺造成的调制解调误差主要由参数Td、Tg、τ、Tm、M/Tm、A、φ、θ、I、R、Kamp、G决定。

仿真分析使用的初始参数值如表1所示。

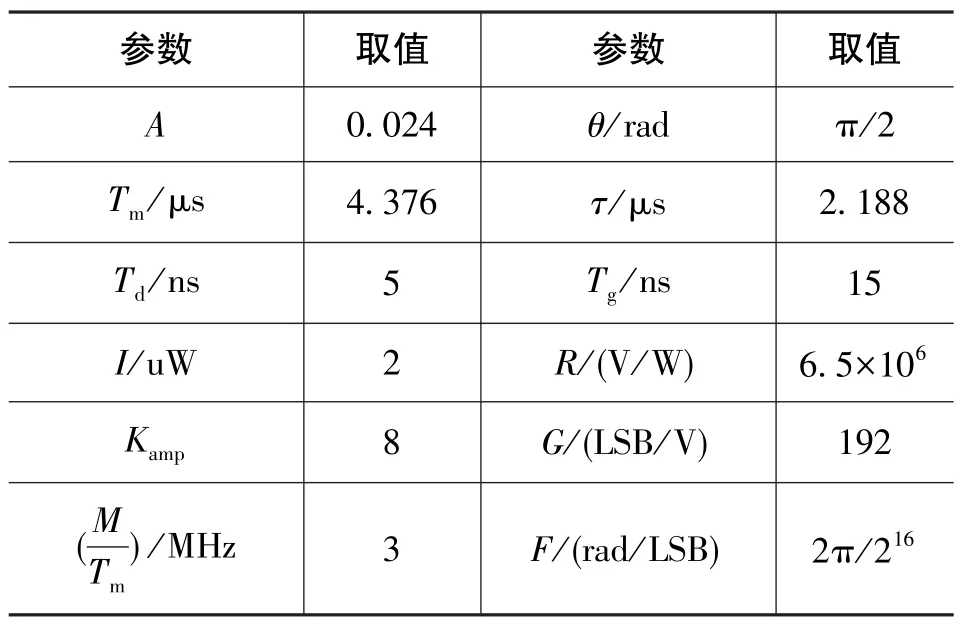
表1 仿真参数初始值Table 1 Initial value of simulation parameters

其中，Tm、I、R、Kamp、G均使用陀螺实际参数。在光纤陀螺中，Tm由电子频率器合成，实际值与理想值存在一定偏差，并且会随着温度的改变发生一定变化。因此在仿真中，改变调制周期，从初始调制周期5μs向正负方向分别偏移0.1μs，即4.9μs～5.1μs，同时设置不同的毛刺宽度15ns、20ns、25ns，仿真结果如图8所示。

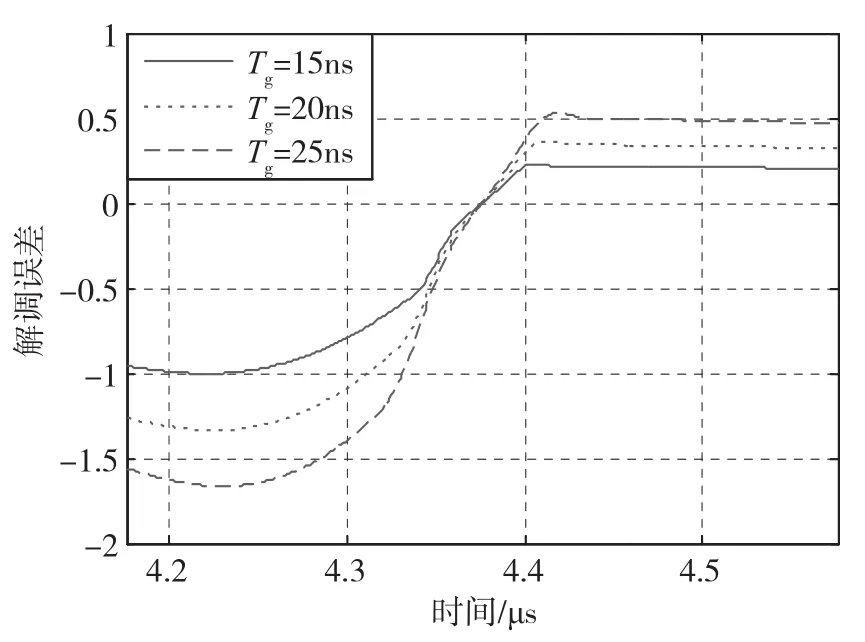
图8 调制周期Tm、毛刺宽度Tg与输出偏置Ω0的关系Fig.8 The relationship betweenTm、TgandΩ0

从图9可以看出，调制周期与本征周期相对于初始值的偏移会改变解调的结果，产生解调误差。当偏移量从0逐渐增加时，干扰信号面积增大，解调误差逐渐增大；当偏移量达到一定大小时，干扰信号面积达到最大值，解调误差最大；此后随着调制周期的增加，干扰信号面积不变，单位时间内的干扰信号面积减小，解调误差响应减小。另一方面，毛刺宽度越大，干扰信号面积越大，解调误差越大。

理想情况下信号调理电路的带宽M/Tm和增益带宽积KampM/Tm为无穷大，但实际电路的增益带宽积KampM/Tm是一个有限常值c。而增益随着温度会产生一定的变化，增益的变化将影响带宽，从而影响能通过电路的谐波次数。信号的高频分量丢失，造成信号的谐波失真，即可间接影响干涉信号幅值和输出结果。此时，分析参数Kamp与分析参数M是等效的。

选取调制周期从初始值偏移＋0.04μs，渡越时间不偏移，即调制周期为5.04μs，渡越时间为2.5μs的情况，利用式(3）、式(5）、式(6）和表1的参数仿真了参数Kamp、M和解调误差的关系。图9(a）表示电路增益带宽积为39MHz时，增益与解调误差的关系；图9(b）表示当Kamp＝8，电路增益带宽积不受限制时，带宽与解调误差的关系。由仿真结果可以看出，随着信号调理电路带宽的增加，能通过的谐波次数增加，干扰脉冲高频分量的丢失减少，时域中干扰信号的面积增大，造成陀螺解调的误差增大。

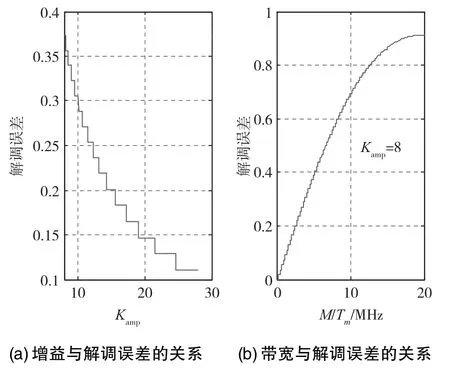
图9 增益G、带宽M/Tm与输出偏置Ω0的关系Fig.9 The relationship betweenG、M/TmandΩ0

在闭环光纤陀螺理想模型的解调环节后引入该解调误差，如图10所示。

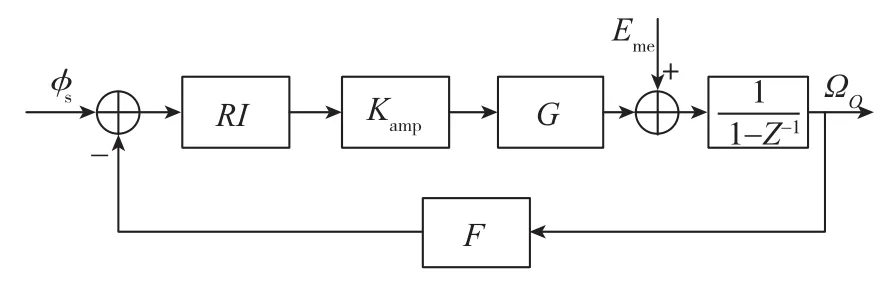
图10 包含DAC毛刺造成解调误差的光纤陀螺简化模型Fig.10 The scheme of FOG model with demodulation errors caused by DAC glitch

在图10中，ϕs表示Sagnac相移，Ω0为陀螺输出角速率，F包括了调制驱动电路增益和集成光学调制器调制效率。

令输入角速度ϕs＝0，根据图10模型写出传递函数即可得输出偏置的表达式：

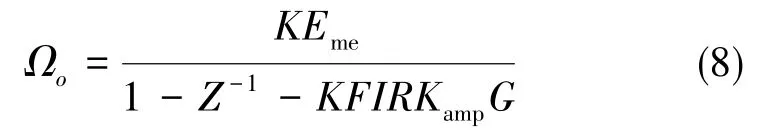
当离散系统采样频率远大于输入信号频率时有1－Z－1≈0，所以当系统输入、输出稳定时，可表示为：

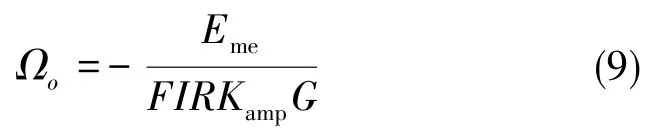
3 DAC毛刺对光纤陀螺调制解调的影响实验与分析

3.1 实验方案

本文需要通过实验验证解调误差产生的区域、解调误差的大小。由于闭环检测的阶梯波是反馈形成的，且复位时间短，而开环检测的阶梯波可以人为地控制，因此对光纤陀螺进行开环检测实验［9］，如图 11 所示。

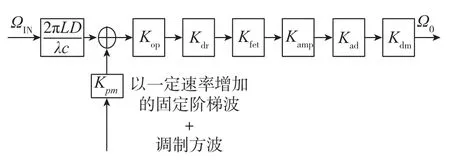
图11 光纤陀螺开环测试简化框图Fig.11 The simplified frame graph of IFOG open⁃loop test

取消光纤陀螺的阶梯波反馈，在调制器上增加2种信号，一种是方波调制信号，另一种是固定台阶的阶梯波信号，且阶梯波以缓慢的速率以1bit增加，复位周期约为20min。在实验中，将经数字信号处理模块解调后的值直接作为输出进行采集，并将固定阶梯波的台阶值同时作为输出进行采集。

3.2 数据分析

采集结果中包括高频噪声信号与低频误差信号，为清晰地表示出DAC毛刺造成的调制解调误差，采取平滑优先方法(Smoothness Priors Method，SPM）对数据进行预处理，以消除其中的高频噪声项，提取低频非平稳趋势项［10］。

采集的解调信号z包含平稳项zstat和非平稳趋势项ztrend2部分：

提取非平稳趋势项部分后可表示为：

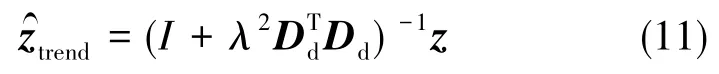
其中，λ为平滑参数，设置为500即可有效地去除原信号中的高频噪声项；Dd∈R(N－d）×N是用离散结果表示的d阶微分，当其阶次为2时可很好地估算信号中的非周期趋势项，取Dd的阶次为2，表示为：

3.3 实验结果

不改变调制周期Tm，测试采集开环输出的结果，将陀螺采集得到的数据绘制成曲线如图12所示。其中，由图12(a）对应解调输出值随时间的变化结果，图12(b）对应阶梯波数值随时间的变化。

对数据进行SPM提取趋势项处理，并取阶梯波码值为16384～32768的区域、阶梯波码值小于16384的区域、阶梯波码值大于32768的区域分别进行1阶线性拟合，拟合结果如图13所示。

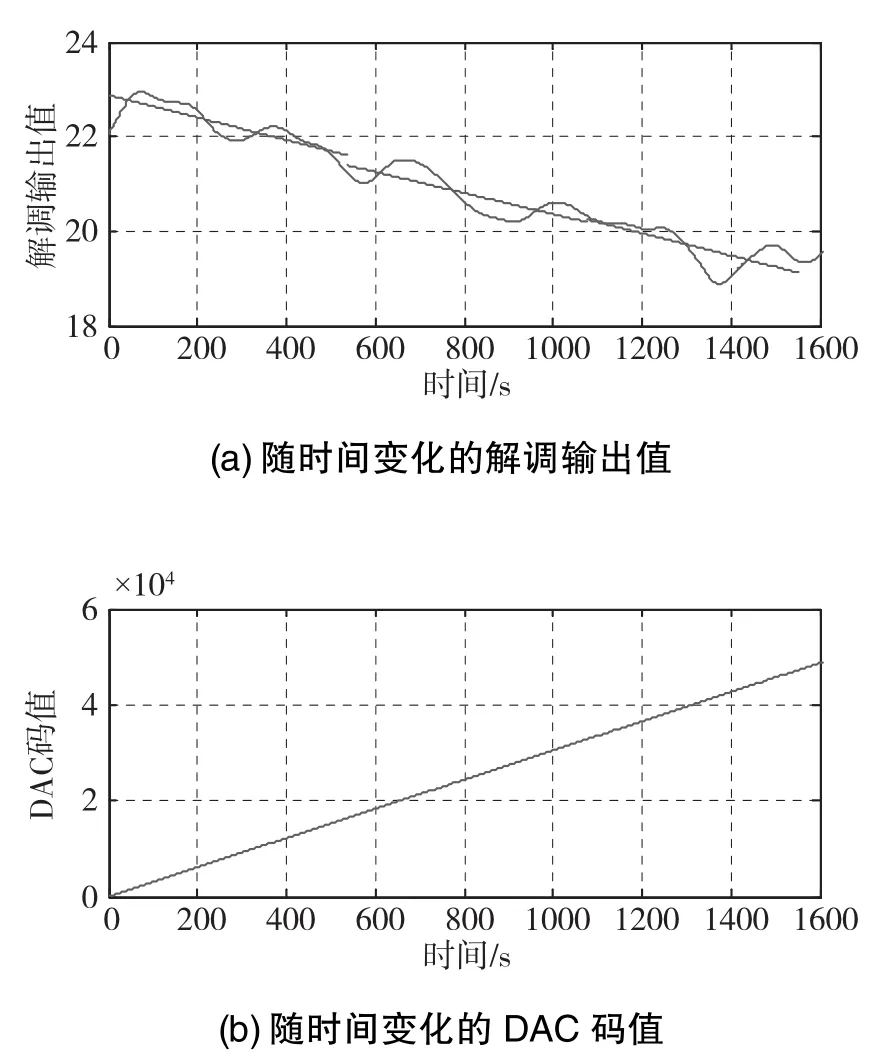
图13 提取趋势项并线性拟合的解调输出结果Fig.13 Trend extraction and linear fitting of the demodulation output

对拟合的3段线段求出平均截距，并进行10组重复实验，得到的数据如表2所示。

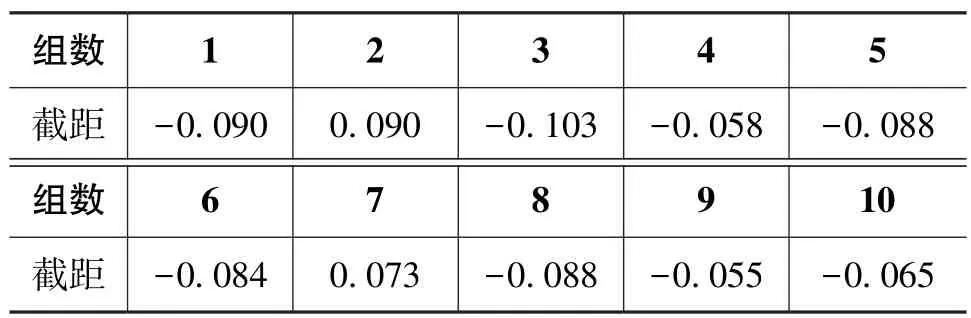
表2 fm＝fp时突变段与非突变段的截距Table 2 Intercept of jump section and whenfm＝fp

经计算得到，突变段(16384～32768）与非突变段的平均突变量为－0.0794。

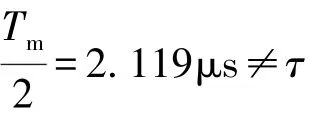
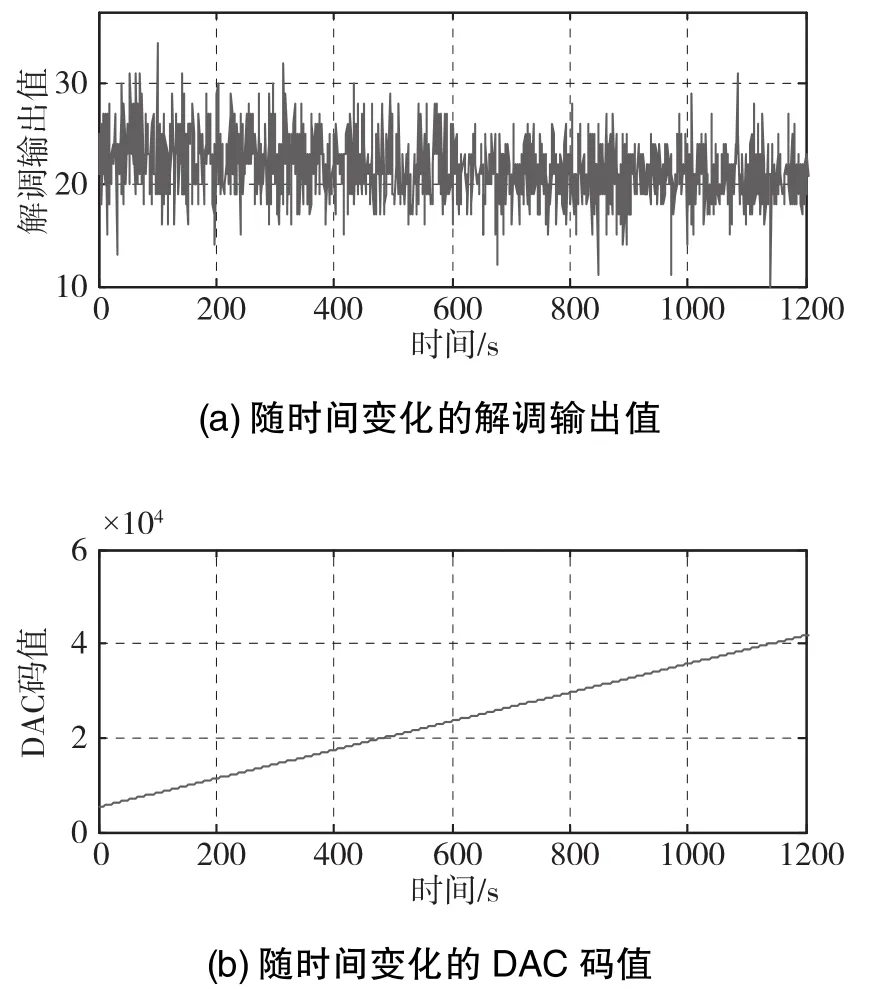
图14 调制频率与本征频率不同时的调制解调输出结果Fig.14 Demodulation output whenfm≠fp

对数据进行SPM提取趋势项处理，并取阶梯波码值为16384～32768的区域、阶梯波码值小于16384的区域、阶梯波码值大于32768的区域分别进行1阶线性拟合，拟合结果如图15所示。

对拟合的3段线段求出平均截距，并进行10组重复实验，得到的数据如表3所示。

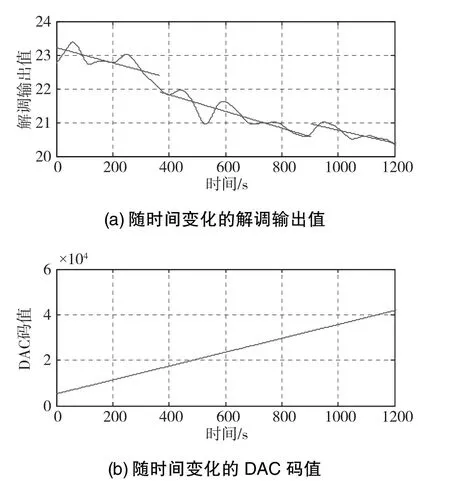
图15 提取趋势项并线性拟合的解调输出结果Fig.15 Trend extraction and linear fitting of the demodulation output

表3 fm≠fp时突变段与非突变段的截距Table 3 Intercept of jump section and whenfm≠fp

经计算得到，突变段(16384～32768）与非突变段的平均突变量为－0.3887。

将实验结果与仿真结果进行对比，如图16所示。

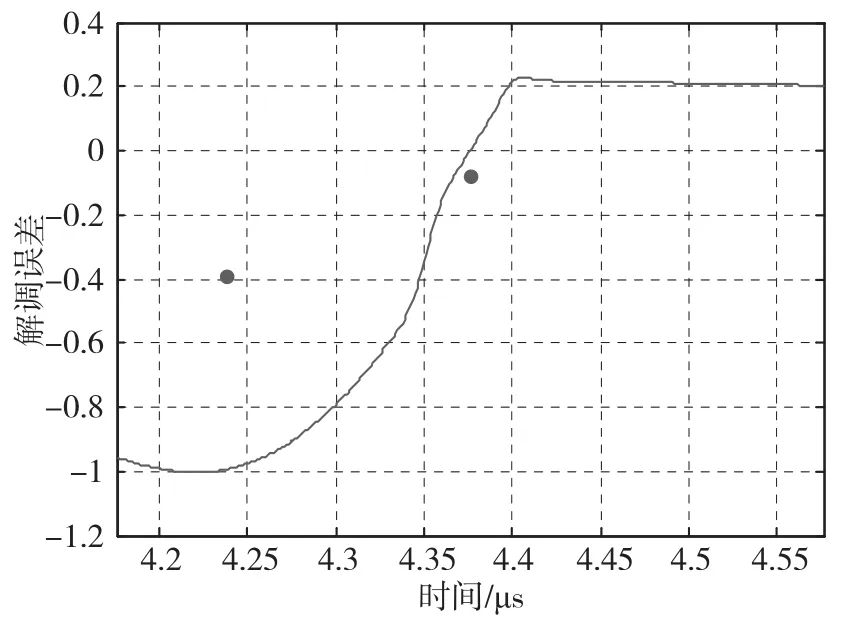
图16 实验与仿真结果对比图Fig.16 The comparison chart of experiment and simulation result

通过2组实验结果及实验与仿真的对比结果可以看出，在调制频率等于本征频率时，解调结果没有明显的突变区域；当调制频率不等于本征频率时，解调结果在毛刺产生区域存在较明显的突变。实验结果与仿真结果的趋势相符合。

4 结论

本文在数字闭环光纤陀螺调制解调原理的基础上建立了DAC毛刺对光纤陀螺调制解调的影响模型，通过仿真分析表明：

1）当调制频率与本征频率不同时，DAC毛刺误差将在光纤陀螺解调结果中造成附加偏置；

2）毛刺宽度和高度、调制驱动电路参数、信号调理电路增益和带宽的变化将影响DAC毛刺造成的解调误差。

通过开环实验验证了对DAC毛刺及其对调制解调影响的正确性，实验结果与理论分析与仿真结果吻合。下一步将利用光纤陀螺的闭环模型，推导DAC毛刺产生的解调误差对陀螺死区的影响，并进行实验验证。

[1]张晓峰,张桂才.闭环光纤陀螺中的死区抑制技术研究[J].压电与声光,2009,31(2）:169⁃171.ZHANG Xiao⁃feng,ZHANG Gui⁃cai.Research on dead zone error reduction technique in closed⁃loop fiber optic gyroscope[J].Piezoelectrics ＆ Acoustooptics,2009,31(2）:169⁃171.

[2]Lefèvre H C.The fiber⁃optic gyroscope（2rd）[M].Artech House,2014.

[3]于海成,王巍,王军龙.光纤陀螺反馈回路非线性的影响与对策[J].中国惯性技术学报,2010,18(4）:487⁃492.YU Hai⁃cheng,WANG Wei,WANG Jun⁃long.Effect and suppression method of feedback loop nonlinearities in FOG[J].Journal of Chinese Inertial Technology,2010,18(4）:487⁃492

[4]Kester W.Evaluating high speed DAC performance[J].Analog Device,2006.

[5]Rapuano S,Balestrieri E,Daponte P,et al.Experimental investigation on DAC glitch measurement[C].Proceedings of 20thIMEKO World Congress,Busan,South Korea,Me⁃trology for Green Growth,2012.

[6]Devices A.High speed design seminar[M].Analog Serv⁃ices,1990.

[7]李春明,孙圣和.数/模转换器输出毛刺对数字合成信号影响的分析及其消除方法[J].仪器仪表学报,1996(6）:561⁃565.LI Chun⁃ming,SUN Sheng⁃he.An analysis of the effect of DAC glitches on digitally synthesized signals and deglitching method[J].Chinese Journal of Scientist Instrument,1996(6）:561⁃565.

[8]金靖,潘雄,宋凝芳,等.方波调制误差对光纤陀螺的影响分析与实验[J].红外与激光工程,2008,37(2）:355⁃358.JIN Jing,PAN Xiong,SONG Ning⁃fang,et al.Analyses and experiments of effects of square wave modulation errors on fiber optic gyroscope[J].Infrared and Laser En⁃gineering,2008,37(2）:355⁃358.

[9]Lo P H,Kovacs R A.Fiber optic gyroscope with reduced non⁃linearity at low angular rates[C].Guidance and Control 1998:Proceedings of the Annual AAS Rocky Mountain Guidance and Control Conference,Breckenridge,Colorado,1998,43:375⁃387.

[10]潘学萍,孙晓波,张丽钦.一种消除电力系统受扰轨迹非平稳趋势项的方法[J].电力自动化设备,2010,30(6）:63⁃66.PAN Xue⁃ping,SUN Xiao⁃bo,ZHANG Li⁃qin.Elimination of non⁃stationary trending component in disturbed trajectory of power system[J].Electric Power Automation Equipment,2010,30(6）:63⁃66.

Effect of DAC Glitch on Correlation Modulation in Digital Closed⁃loop IFOG

DING Jiang⁃ting1,PAN Xiong1,ZHANG Hui2
(1.School of Instrumentation Science and Opto⁃electronics Engineering,Beihang University,Beijing 100191;2.Xi'an Advanced Control Technologies Research Institute,Xi'an 710065）

V241.5＋9

A

1674⁃5558(2017）03⁃01344

10.3969/j.issn.1674⁃5558.2017.05.011

2016⁃12⁃03

丁江婷，女，硕士，光学工程专业，研究方向为光纤陀螺的相关检测。