雷暴风激励下简支梁式屋盖结构的风振响应参数化分析

周 臻， 丁惠敏， 孔祥羽

(东南大学 混凝土及预应力混凝土结构教育部重点实验室，南京 210096)

雷暴风激励下简支梁式屋盖结构的风振响应参数化分析

周 臻， 丁惠敏， 孔祥羽

(东南大学 混凝土及预应力混凝土结构教育部重点实验室，南京 210096)

基于时域分析方法对简支梁式屋盖结构在雷暴冲击风作用下的风振响应进行参数化研究。利用混合随机模型对雷暴冲击风强风荷载进行数值模拟，其中平均风采用Wood竖直风剖面方程与Holmes经验模型模拟，脉动风采用基于Kaimal目标谱的自回归AR模型模拟，谱分析结果表明雷暴风模拟结果具有较好的精度；分析了结构主要参数和雷暴风参数对结构风振响应的影响，结果表明：结构刚度、跨度、最大风速半径及风暴移动速度对结构的风振响应影响较大。针对雷暴风中平均风和脉动风响应均随时间变化的特性，采用基于包络概念的整体风振系数计算方法，分别研究了不同参数下的整体位移风振系数和整体荷载风振系数，结果表明，采用结构整体位移风振系数进行雷暴风等效静风荷载分析具有更高的精度。

雷暴冲击风；混合随机模型；参数分析；风振系数

风荷载是大跨屋盖结构的重要设计荷载。目前大跨结构的抗风研究和设计分析主要依据大气边界层风场特性[1-3]，但研究表明，具有强冲击效应的雷暴风会对屋盖结构和高层建筑产生强烈的破坏作用[4-5]。Fujita[6]记录了雷暴冲击风距地面4.9 m高处的最高水平风速可达67 m/s。由此可见，研究雷暴风作用下大跨屋盖结构的抗风设计具有重要意义。

目前围绕雷暴风的风场特性和数值模拟和CFD模拟开展了较多研究[7-8]，但对整体结构的动力响应研究较少。近年来，一些学者采用数值模拟或风洞试验对悬挑结构[9]、输电线路[10]等在雷暴风作用下的风致振动响应进行了研究。潘峰[4]将大跨屋盖与下部支撑结构简化为弹簧振子模型，研究了其在冲击风作用下的水平振动响应，但未考虑大跨屋盖的竖向弯曲振动。

本文针对简支梁式屋盖结构力学模型，采用混合随机模型模拟结构的雷暴冲击风速时程，基于时域分析方法研究不同结构参数和风参数对结构风振响应的影响规律，并对比分析不同风振系数计算方法的结果。

1 雷暴冲击风的数值模拟

雷暴冲击风不满足目前常用的大气边界层风剖面沿高度指数或对数增长的特性，近地面最高风速远大于根据大气边界层风速得到的值，其风场属于一种非稳态的随机过程，平均风速随时间而变化，雷暴的射流的强度，持续时间等均具有非稳态的特点，且风暴本身是一个运动的过程。

本文采用混合随机模型，在任意高度z、任意时间t时，雷暴冲击风仍可以表示为平均风和脉动风的组合形式：

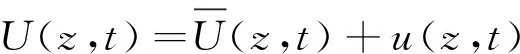
(1)

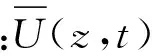
1.1平均风模拟

本文应用Wood竖直风剖面方程与Holmes经验模型模拟平均风场。平均风随时间变化，表示为

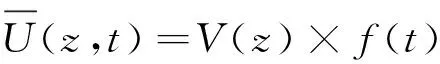
(2)

关于V(z)为随高度变化的竖直风剖面，其wood模型：

V(z)=1.55(z/δ)1/6[1-erf(0.7z/δ)]×Vmax

(3)

式中:z为距离地面的高度；δ为风速最大剖面高度的一半，取为400 m；erf是容错函数；Vmax是最大风速，取为80 m/s。

关于时间函数f(t)为最大值等于1的时间函数。f(t)用来描述雷暴冲击风平均风速随时间变化的规律。Holmes提出径向射流速度和风暴移动速度的概念，同一高度上，径向风速可以表示为

(4)

式中:Vr,max为径向剖面的最大风速，本文取47 m/s；rmax为半径长度，本文取1 000 m；Rr为径向辐射范围，本文取700 m。

1.2脉动风模拟

雷暴风的脉动风速是一个非平稳的随机过程。Chay[11]认为是该时刻平均风速的0.08倍～0.11倍。因此假定脉动风速的频域特性不随时间改变，将脉动风速时程写成一随时间变化的幅值调制单位函数和一服从标准正态分布的高斯随机过程的乘积，即：

u(z,t)=a(z,t)×k(z,t)

(5)

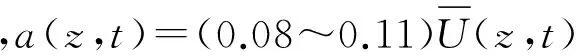
(6)

式中:u*为剪切风速，本文取1.76 m/s[9];U(z)为平均风速;z为高度;ω为角频率。

结构上各点风速具有一定相关性，取两点间的相关系数为γ(z1,z2,ω)，

γ(z1,z2,ω)=

(7)

式中，cx=6;cy=16;cz=10。

2 结构分析模型与风振响应分析方法

2.1分析基准模型

本文分析模型是一简支梁式屋盖结构力学模型。基本算例如图1所示，具体参数如下：跨度为L=50 m，线刚度为EI/L=1.48×1010Pa/m，单位质量m=780 kg/m，结构处于高度H=40 m处，风暴移动半径V=12 m/s，最大风速半径rmax=1 000 m，湍流强度取0.11。Letchford[13]研究了在雷暴风作用下立方体表面沿中轴线方向的风压分布，本节计算雷暴风致响应时采用Chay试验X/D=1时的风压系数结果，此时风压系数较大。其中X/D为立方体距风机喷口的长度与风机喷口直径的比值。图1为简支梁上各点风压系数拟合结果。

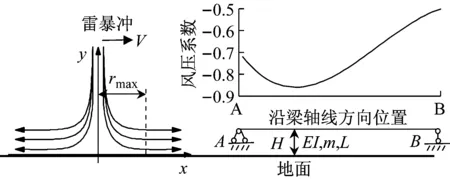
图1 分析模型及其风压系数拟合

2.2风速时程的模拟与谱分析

本文采用AR法[12]模拟脉动风随机过程。将基准模型分为51个节点，计算每个节点的雷暴冲击风风速时程，图2(a)为跨中节点矢量合成的平均风速，图2(b)为脉动风风速时程，可以看出在两个波峰位置脉动风速波动尤为剧烈。图2(c)为模拟的雷暴风风速时程，在40 s，95 s周围有明显的两个波峰，风速最大接近100 m/s，而常规风一般在30 m/s左右，由此可见，雷暴冲击风比常规风更加猛烈。图2(d)为脉动风随机过程功率谱示意图，可以看出，模拟功率谱围绕水平向目标模拟功率谱(Kaimal谱)上下波动，吻合情况较好。

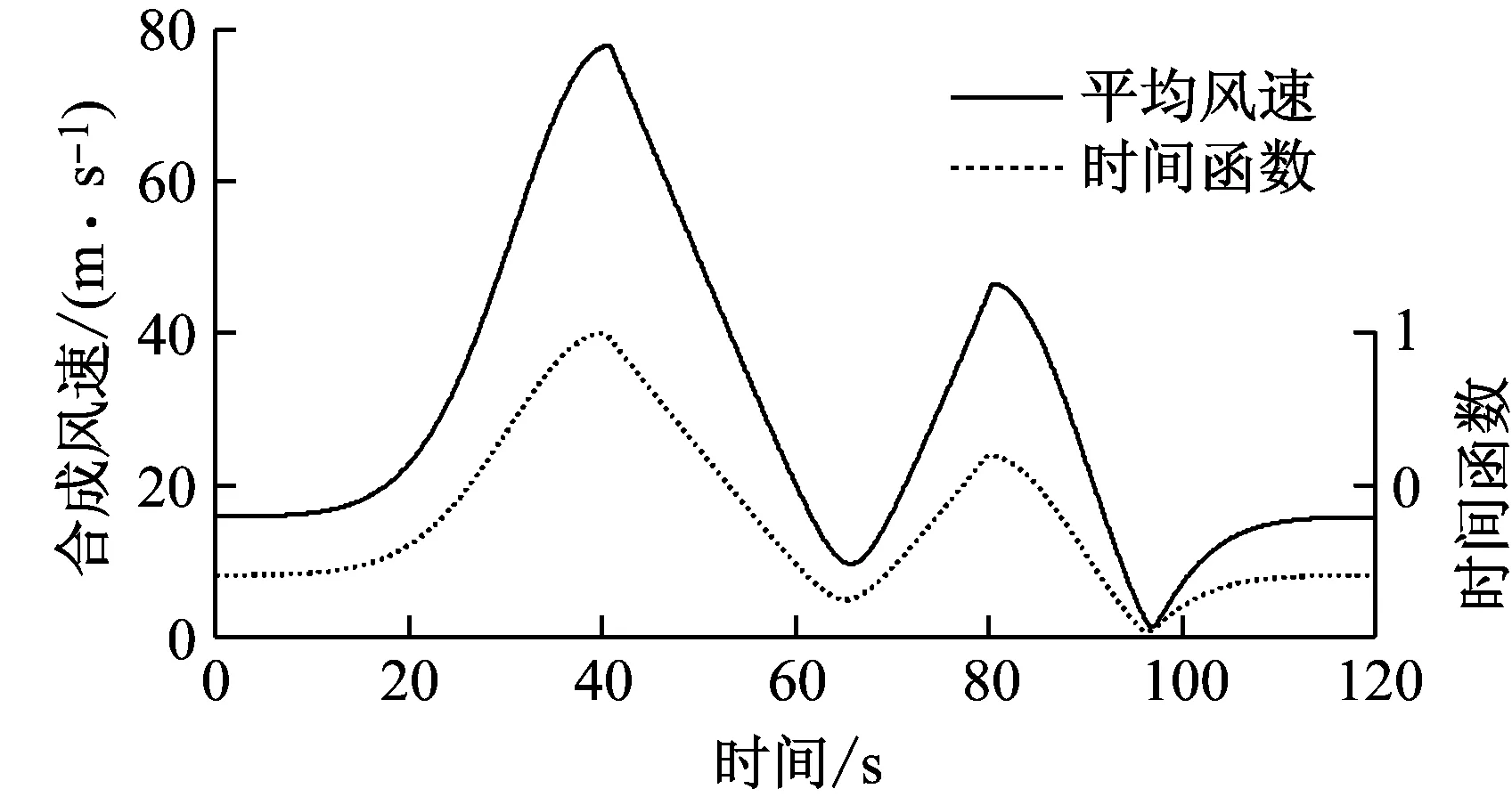
(a) 平均风速和时间函数图

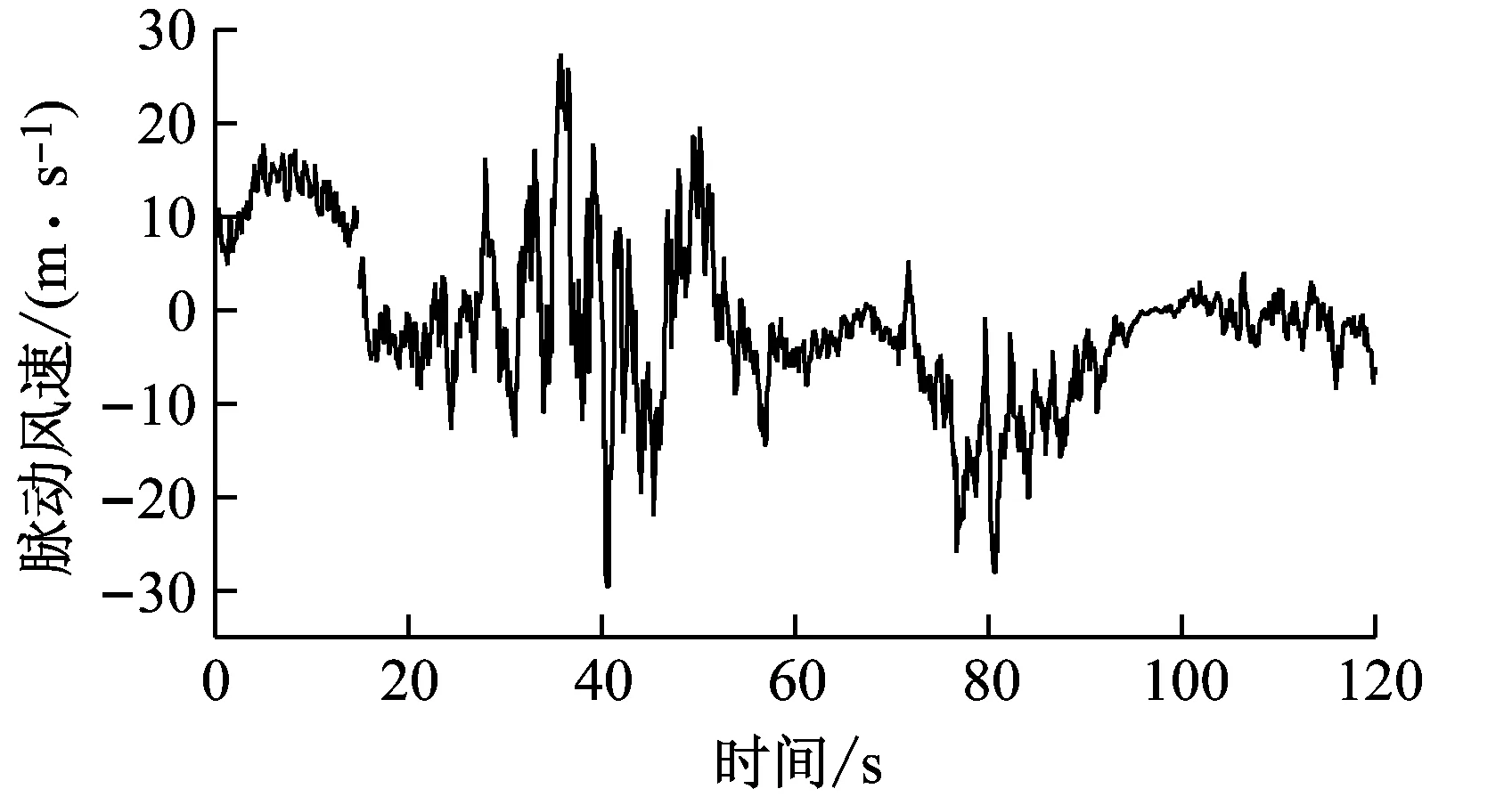
(b) 脉动风风速

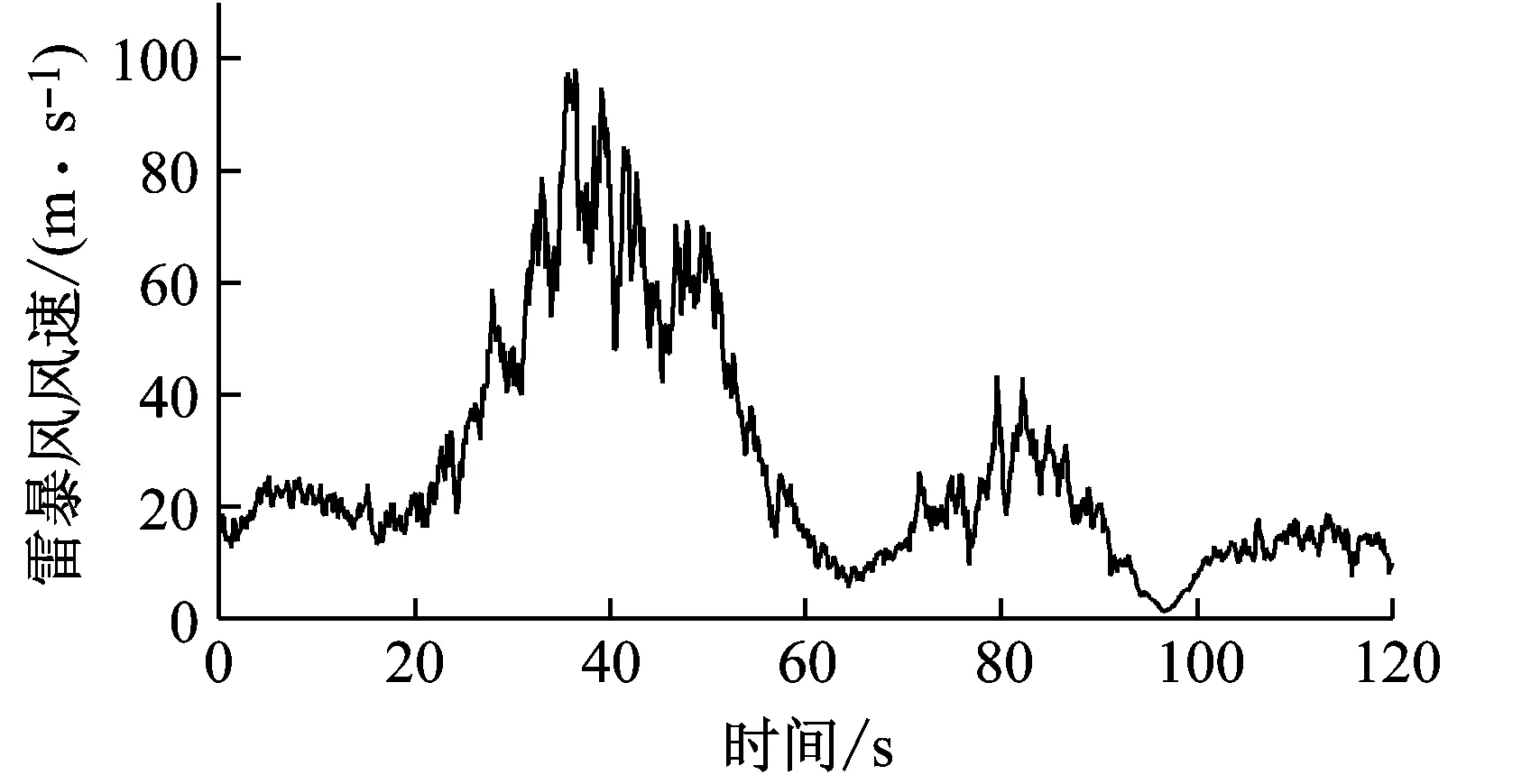
(c) 雷暴冲击风风速时程

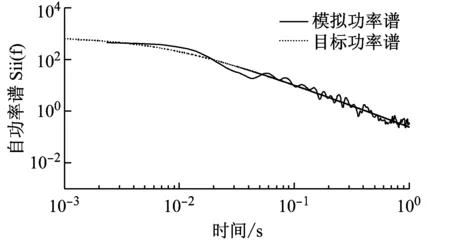
(d) 模拟功率谱与目标功率谱对比图

2.3风振响应分析

在进行风振响应分析时，其结构动力有限元基本方程一般可表示为

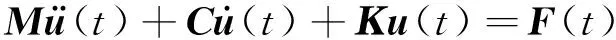
(8)

(9)

式中：vp为i节点处的平均风风速，且vm为i节点处的脉动风风速，且μsi为节点i所在位置的体型系数；ρ为空气密度，取为1.225 kg/m3；Ai为节点对应风压面积。

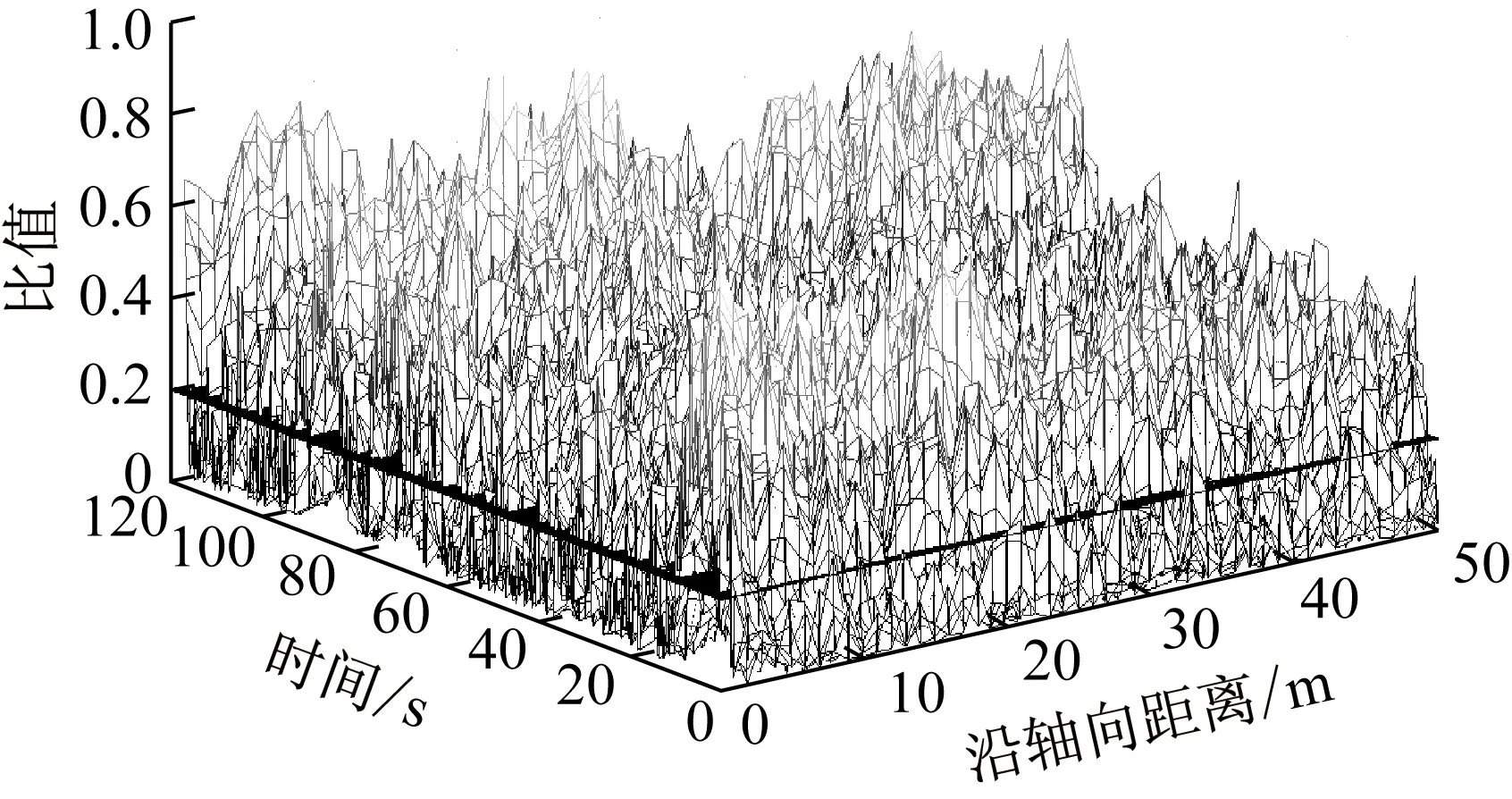
图3 脉动风速与平均风速比值

由于平均风也具有时变性，本文对平均风荷载和雷暴风荷载作用响应均采用时程分析法，结果如图4所示。将图2(c)与图4(a)比，发现位移时程，和风速时程分布规律相似，在40 s附近有一个明显的峰值在95 s附近有一较小的峰值，梁跨中最大位移达到140 mm，而在其他时间段位移一般只有5 mm左右，差距较大。而图4(b)则反映了在这两个时间段加速度有剧烈的波动，最大加速度约为0.58 m/s2。

2.4风振系数

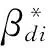
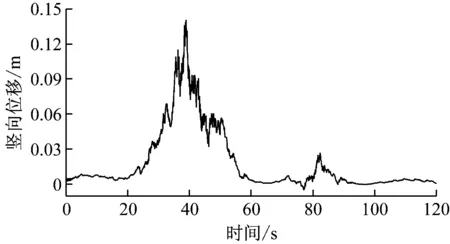
(a) 位移时程图

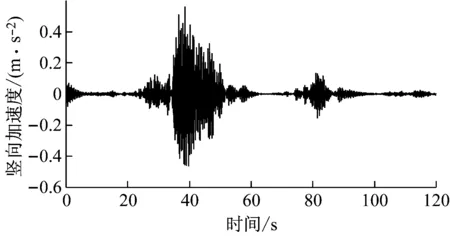
(b) 加速度时程图

Fig.4 Displacement and acceleration response of the mid span nodes under the action of a thunderstorm

(10)

(11)

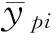
3 结构参数对风振响应的影响

3.1线刚度EI/L

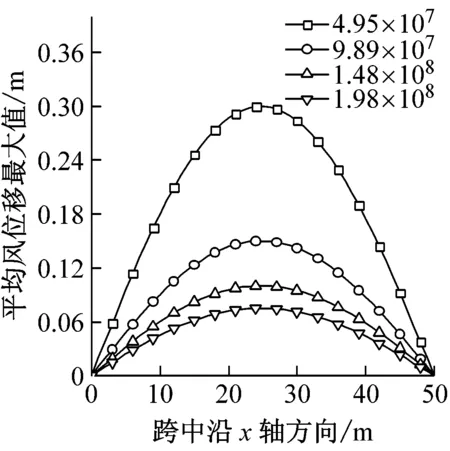
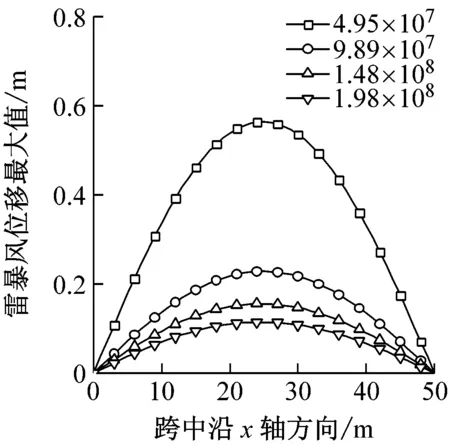
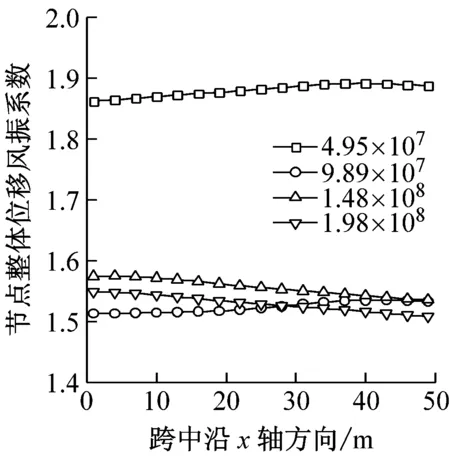
图5给出了线刚度EI/L分别为4.95×107N/m2、9.89×107N/m2、1.48×108N/m2、1.98×108N/m2时结构的风振响应。如下图5(a)和(b)所示，结构在平均风作用下和雷暴风荷载作用下的竖向位移最大响应均随线刚度的增大而减小，减小的幅度在迎风面和背风面较小，但在结构中部则较大，这主要是由于在同一矢跨比下，结构中部附近风荷载体型系数较大，承担的风荷载较多，因此对结构刚度的改变更加敏感。梁上各点节点整体位移风振系数基本上一致，表明节点整体位移风振系数大小与在梁上的位置无关。线刚度在9.89×107～1.98×108N/m2范围内变化对节点整体位移风振系数的影响则较小，从风振系数的角度来看，由于雷暴风作用下和平均风作用下的位移最大响应均同步变化，因此表现在风振系数上，则变化较小(图5(c))。这表明在此范围内，风振系数对刚度不敏感。而当刚度足够小，为4.95×107N/m2时，梁跨中在平均风和雷暴风作用下的最大位移响应与其他刚度下相比显著增大。梁在雷暴风的脉动性更强，产生的位移最大响应是平均风产生的响应的近两倍，风振系数显著增大。

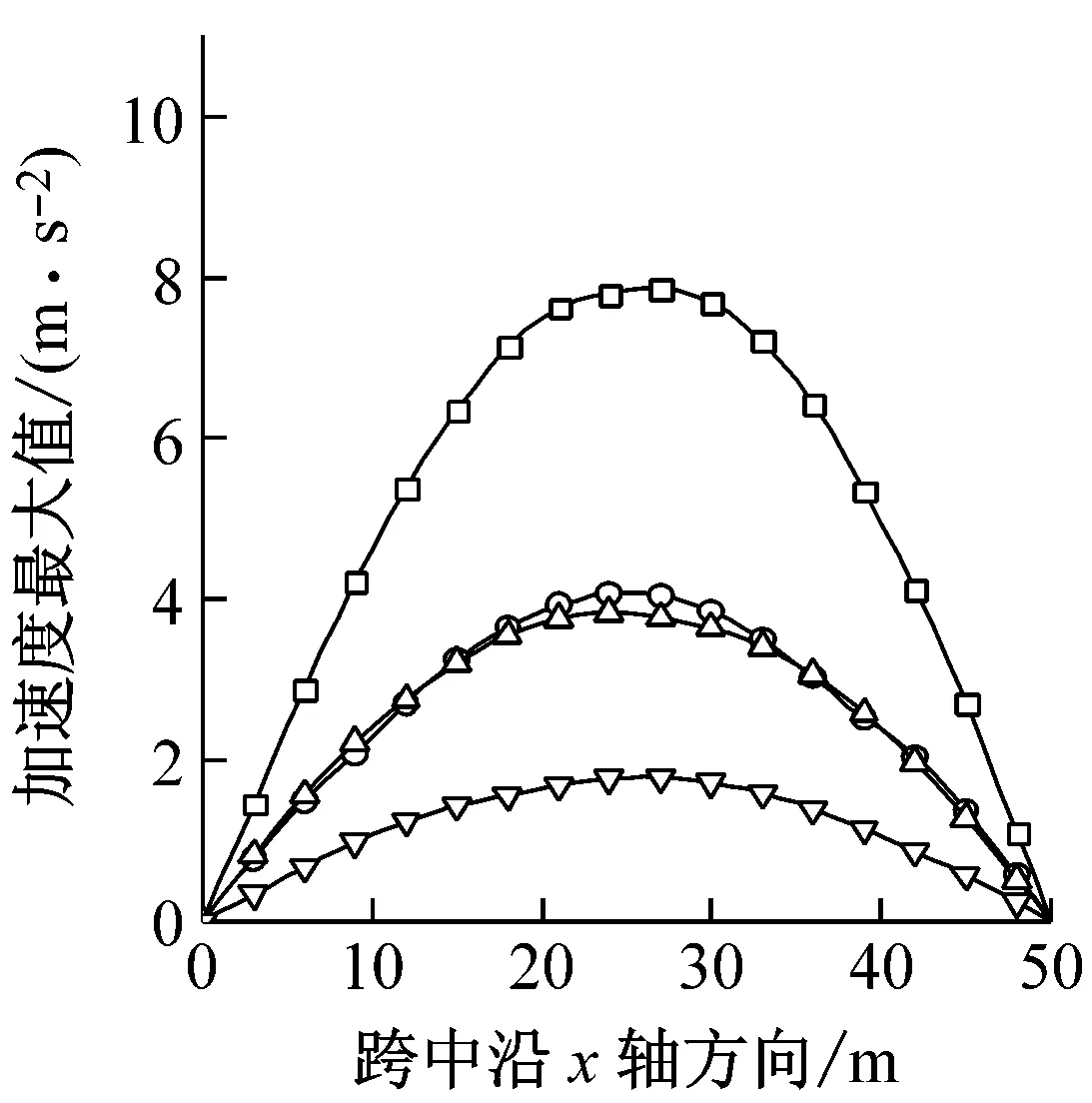
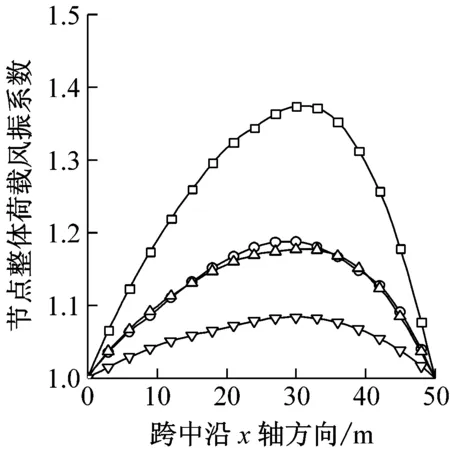
平均风荷载最大值在梁上呈曲线形，因为梁上各点平均风最大风速相同，因此其分布形状与体型系数紧密相关(图5(d))。从图5(f)可以看出，节点整体荷载风振系数随着线刚度的增大而减小，与图5(e)加速度最大值布置规律相似。

3.2跨度L

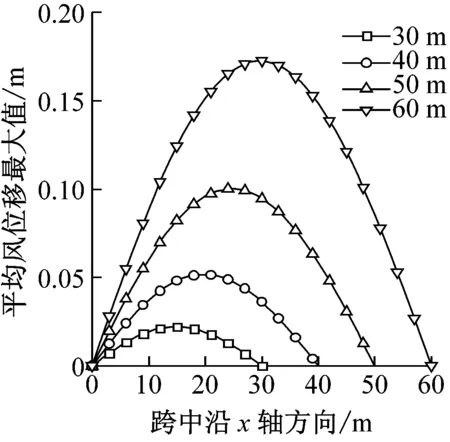
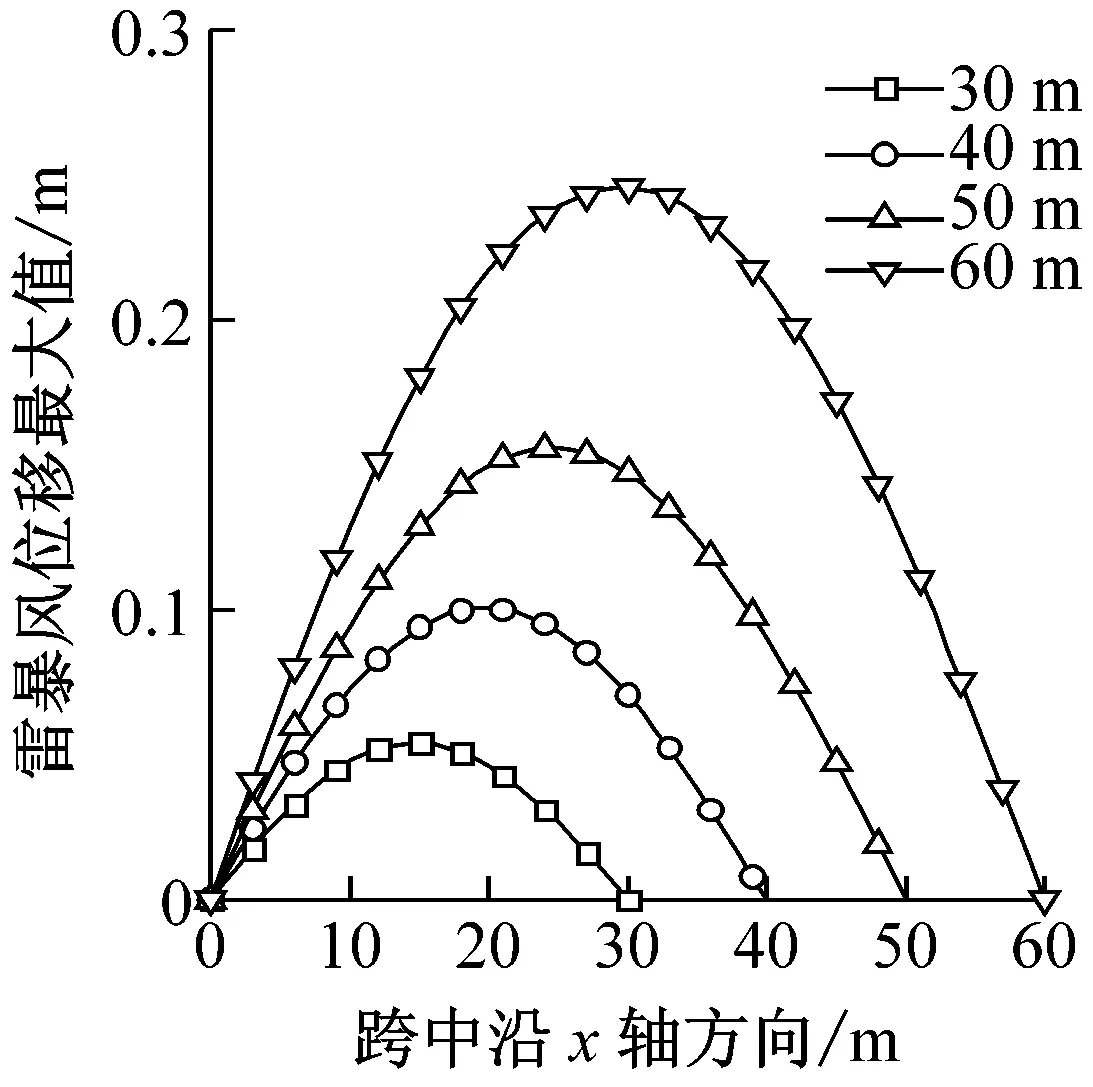
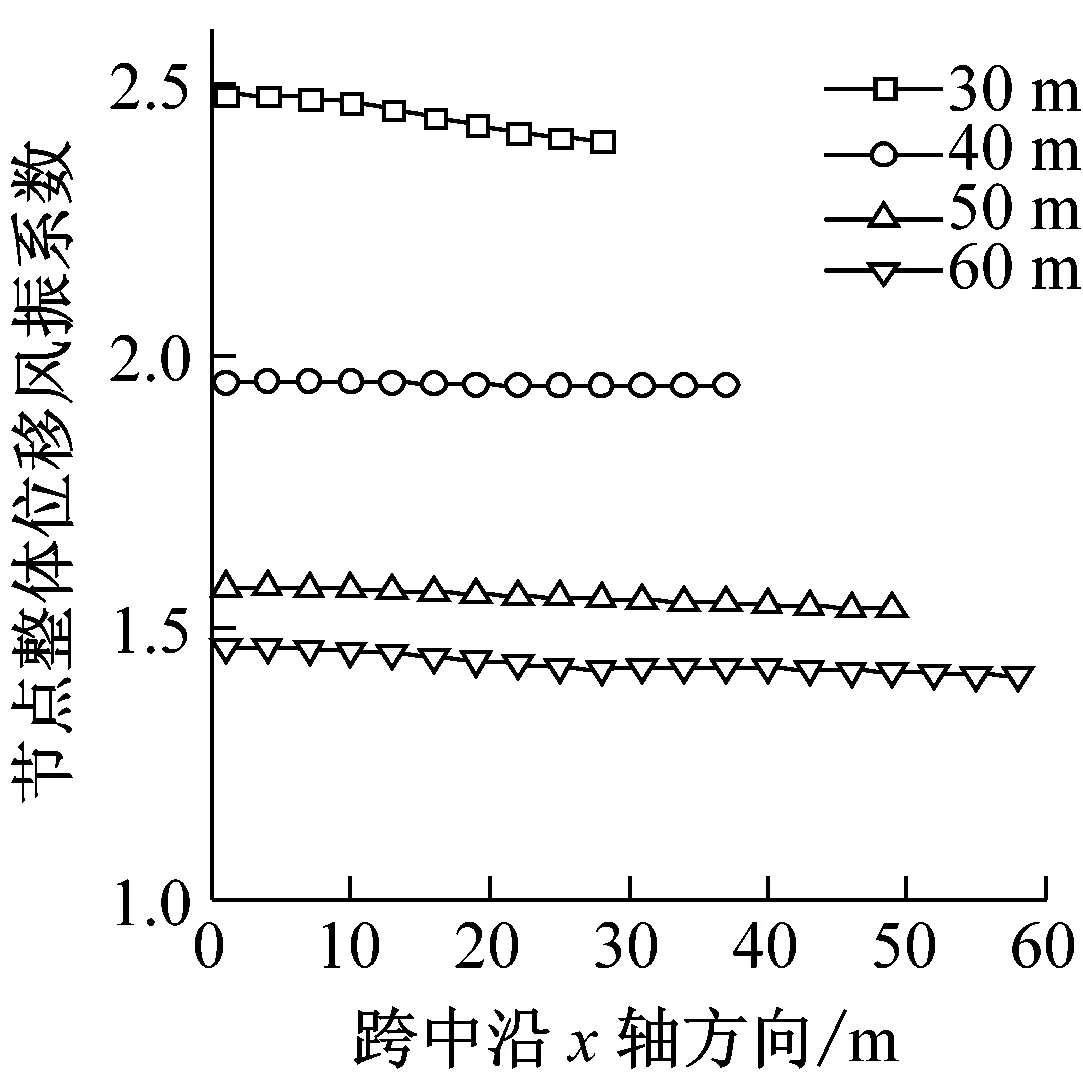
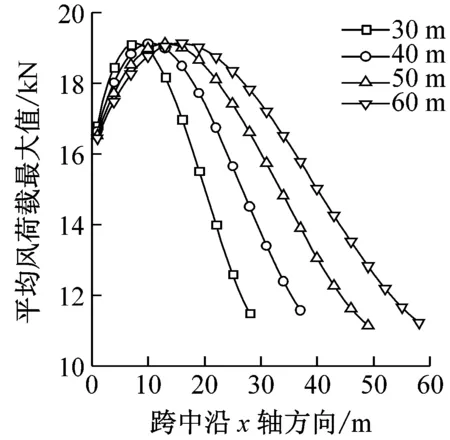
图6给出了跨度L分别为30 m、40 m、50 m、60 m时结构的风振响应。在保证结构线刚度不变的情况下，通过图6可以看出跨度增大，平均风荷载和雷暴风总荷载在梁跨中产生的最大位移都随之增大，节点整体位移风振系数随跨度的增加而减小，由2.45左右减小至1.45左右，说明跨度对梁的节点整体位移风振系数影响显著。平均风最大荷载在离梁左端前10 m随跨度增大而减小，10 m后则随跨度增大而增大，这是由于平均风风速在梁上分布特点决定的。节点整体荷载风振系数在跨度从30 m变化到50 m时随之增大而增大，当跨度达到60 m时，其跨中风振系数减小，与节点加速度最大值分布特性相同，节点加速度也是随着跨度增加先增大后减小。

4 雷暴风参数对风振响应的影响

4.1风场高度H

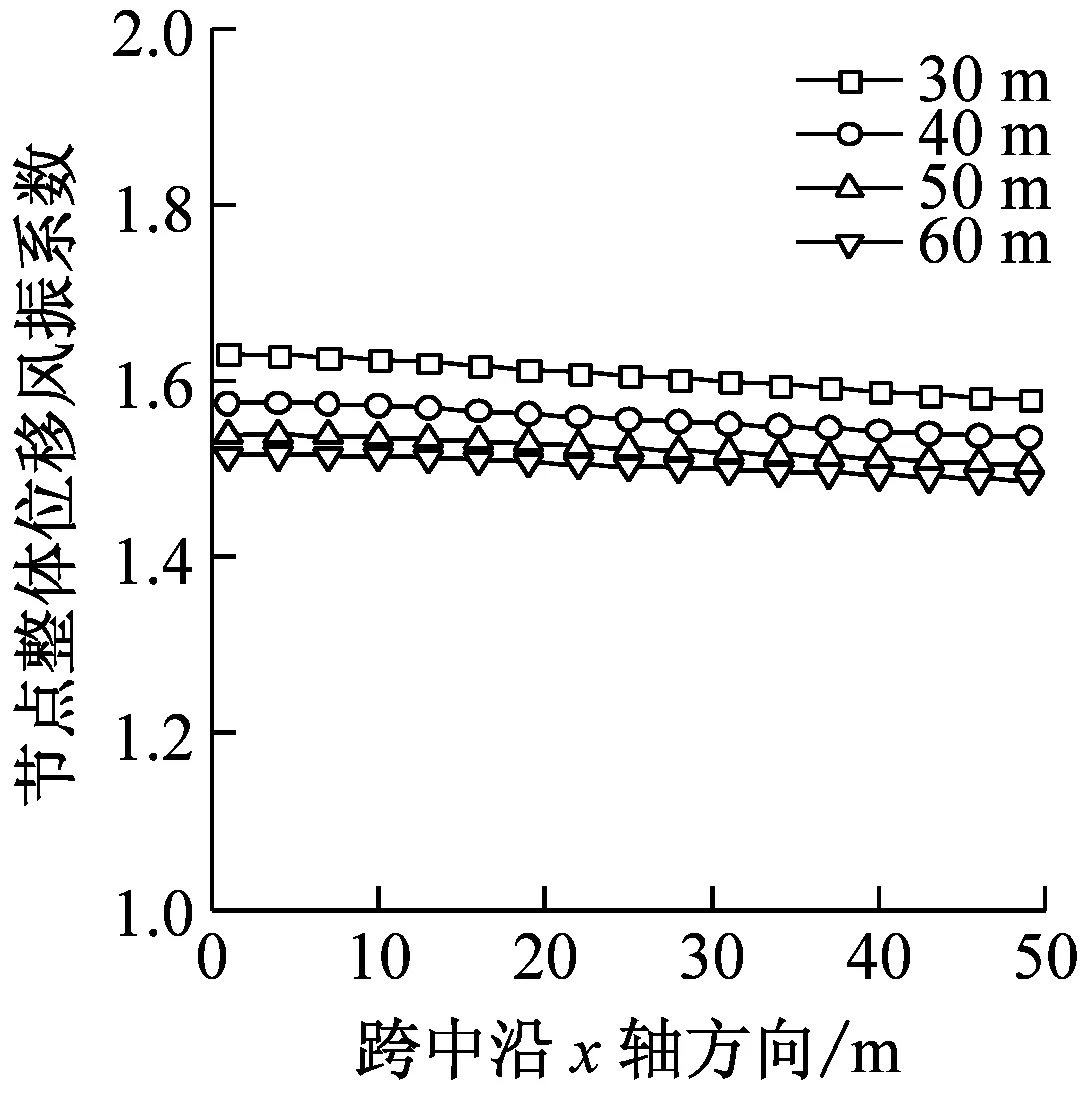
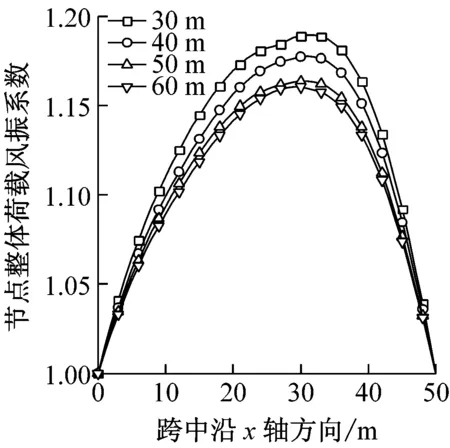
图7给出了跨度H分别为30 m、40 m、50 m、60 m时结构的风振响应。如图7(a)和(b)所示，分别在平均风和雷暴风作用下，结构位移最大响应会随着结构所处位置的高度增大而增大，这是由于在所选范围内即30～60 m，高度的增大会使风速增大从而造成风荷载的增大，不过增大程度较小说明高度对风荷载影响不大。而风振系数和高度成反比，不过影响很小，在1.5～1.65范围内变化。节点整体荷载风振系数受高度影响同样也很小，波动范围在百分位，约为1.17。

4.2风暴移动速度V

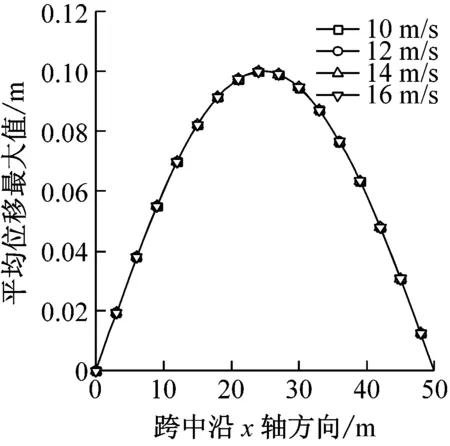
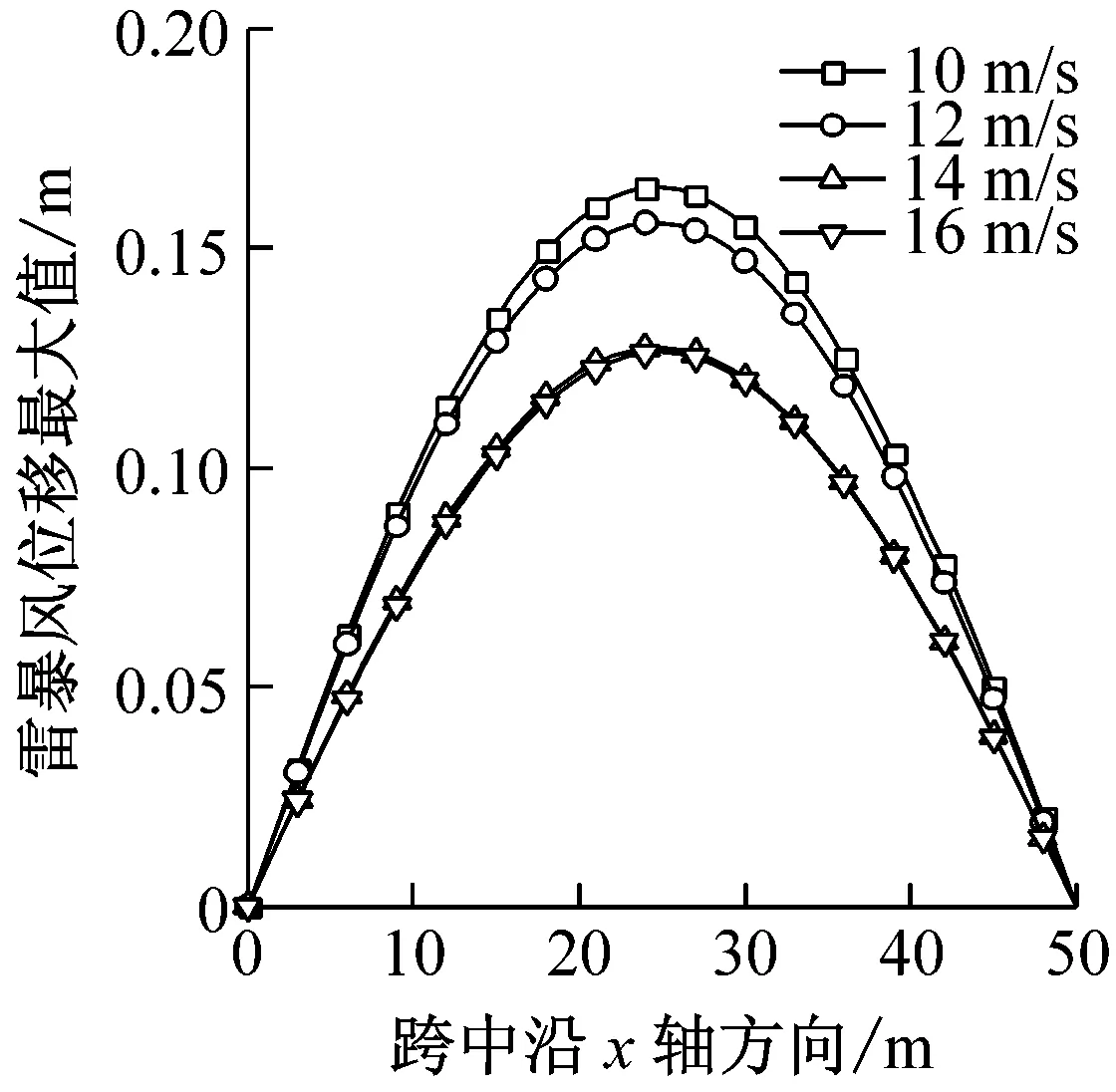
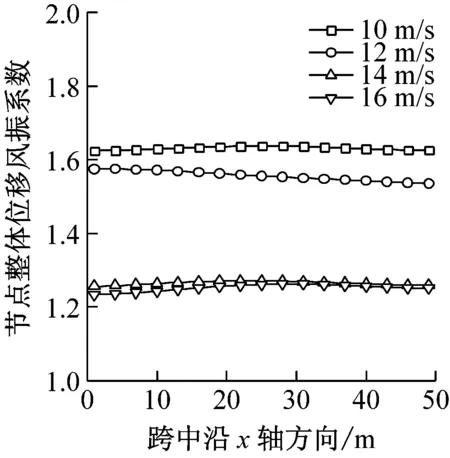
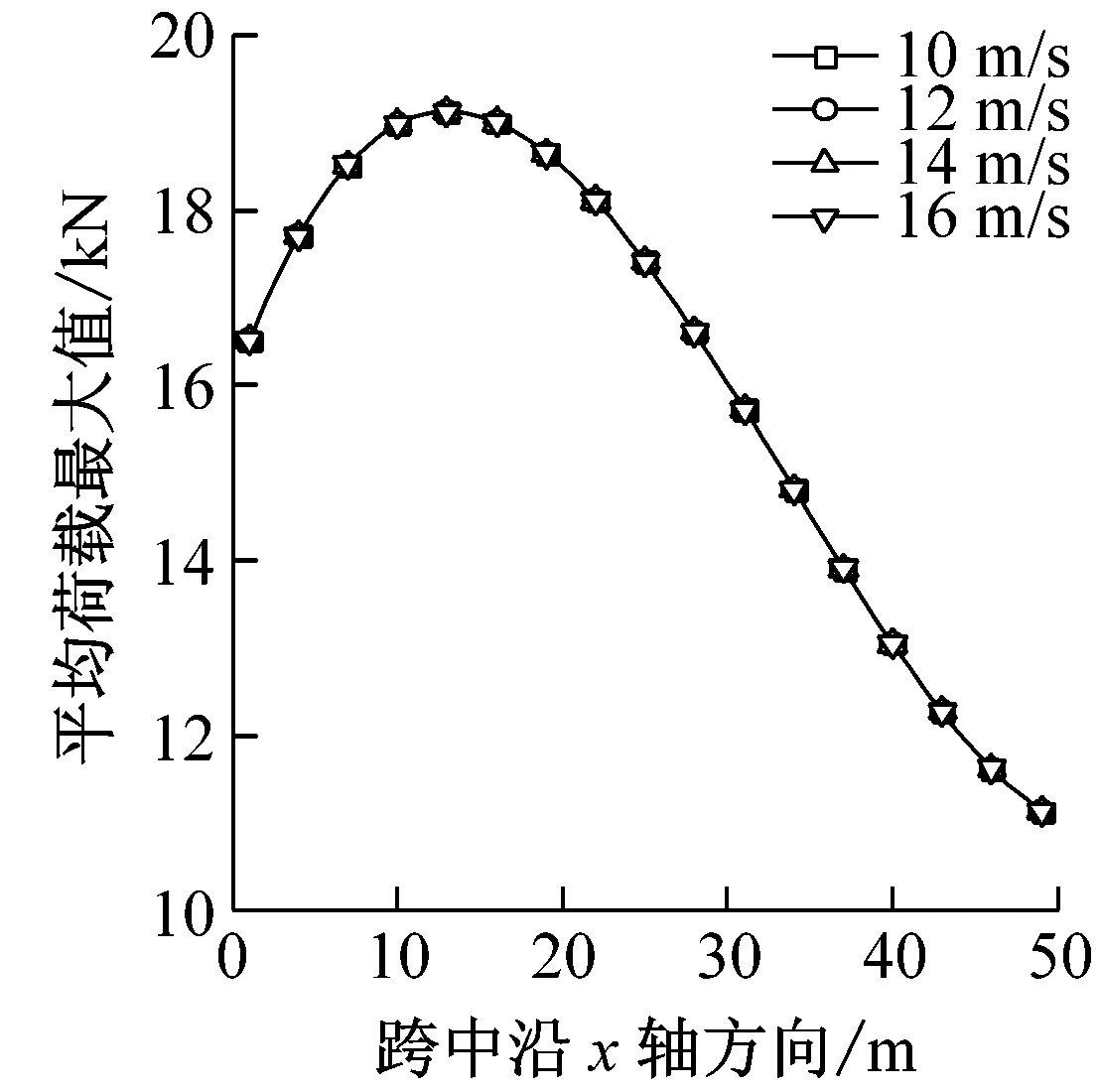
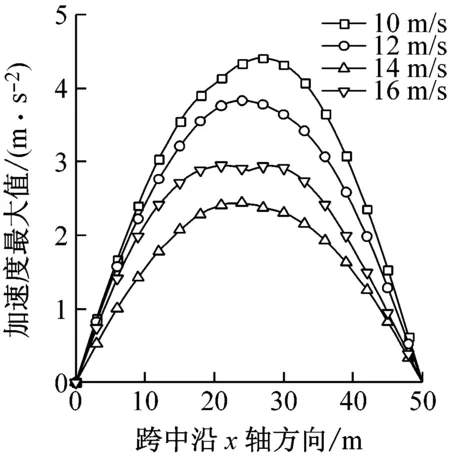
图8给出了风暴移动速度V分别为10 m/s、12 m/s、14 m/s、16 m/s时结构的风振响应。平均风速用的是风暴移动速度与径向风速的矢量合成，因此移动风速直接影响到风速。图8(e)中可以看出，移动风速对平均风荷载最大值大小没有影响(对平均风风速的影响仅在于改变其峰值出现时间)，因此平均风荷载产生的最大位移也相同，如图8(a)所示。从整体上看，移动速度的增加减小了风荷载，因此雷暴风作用下的最大位移响应随移动风速增大而减小，导致节点整体位移风振系数也随风移动速度增大较小。节点整体荷载风振系数随之移动风速先减小后增大，但影响不是很大，系数在1.12～1.22之间波动。

(a)

(b)

(c)

(d)

(e)

(f)

(a)

(b)

(c)

(d)

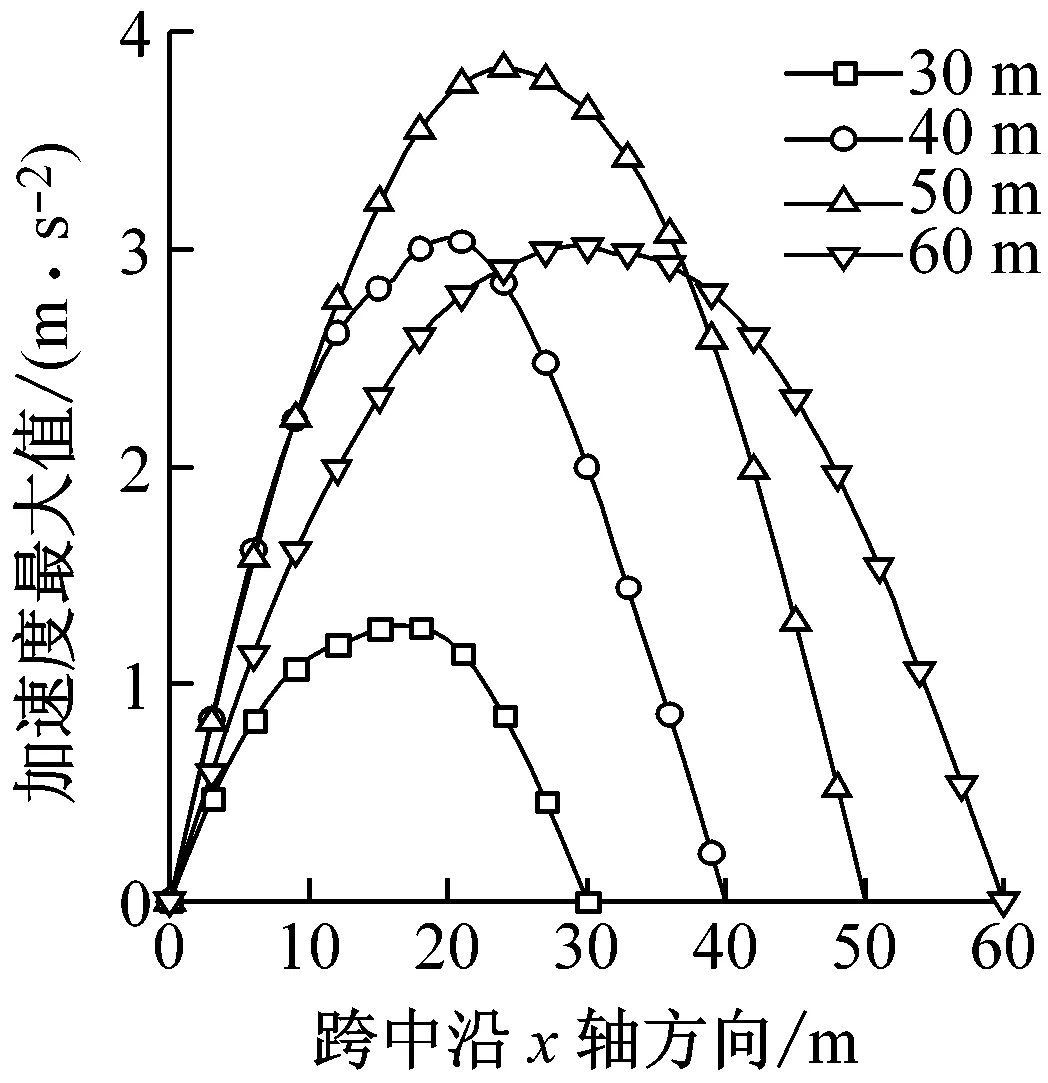
(e)

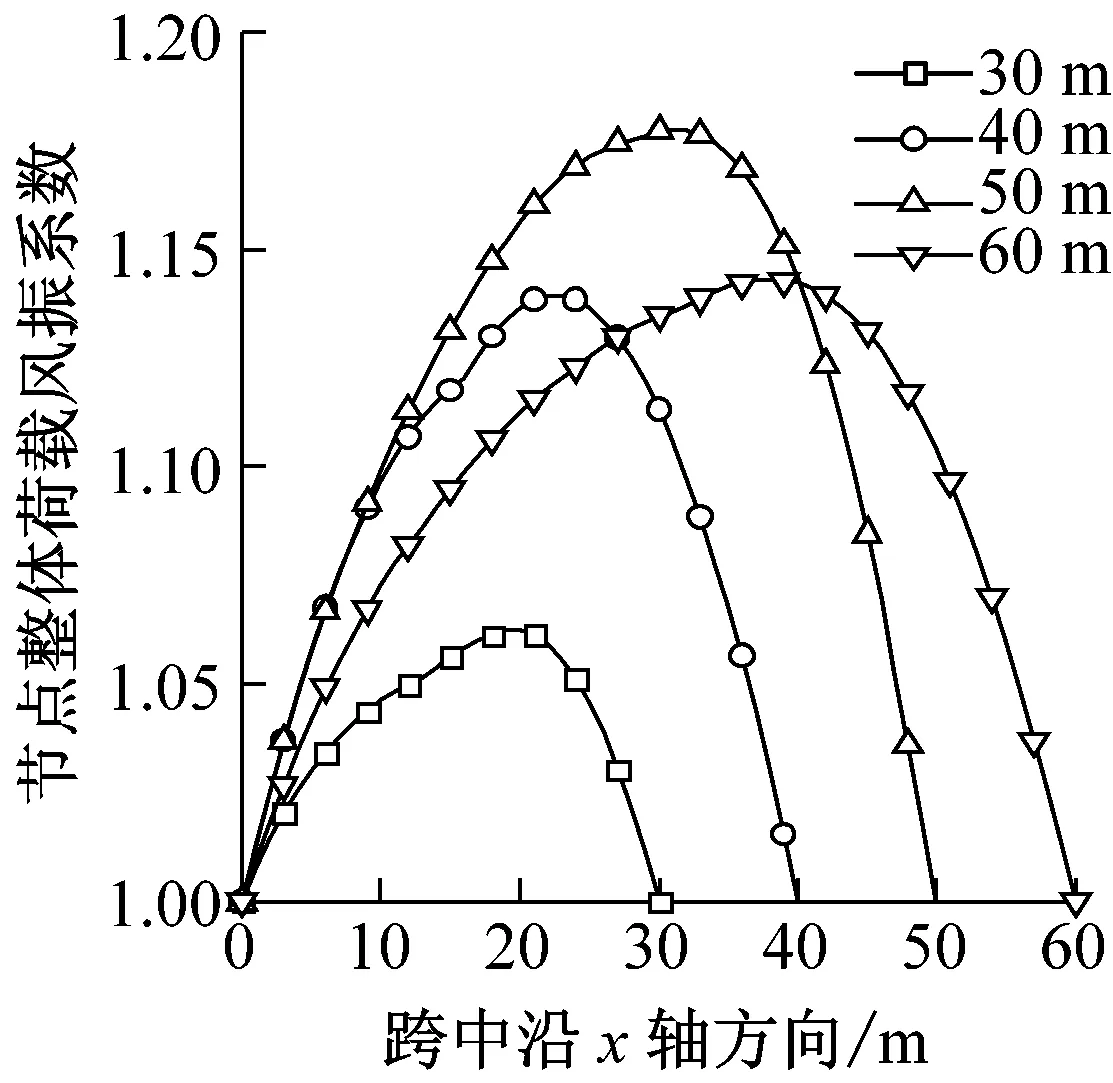
(f)

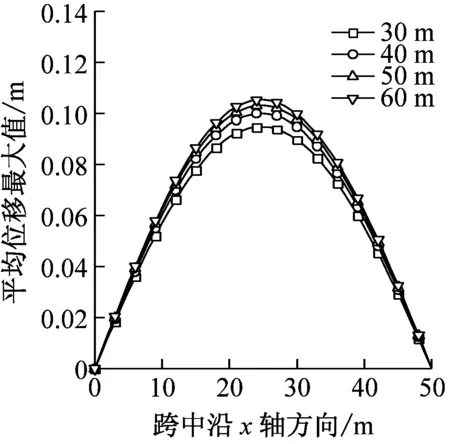
(a)

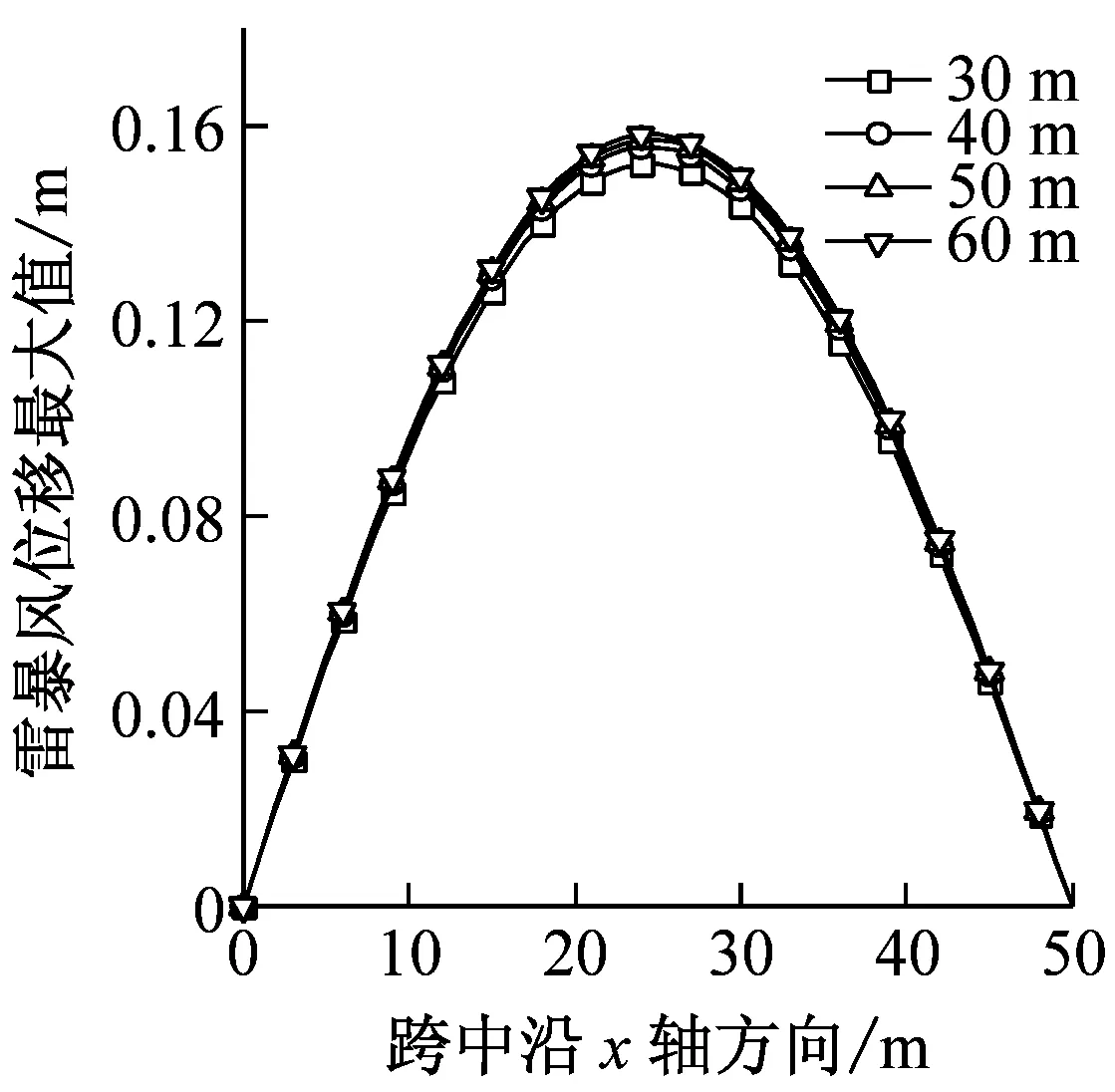
(b)

(c)

(d)

(e)

(f)

(a)

(b)

(c)

(d)

(e)

(f)

4.3最大风速半径rmax

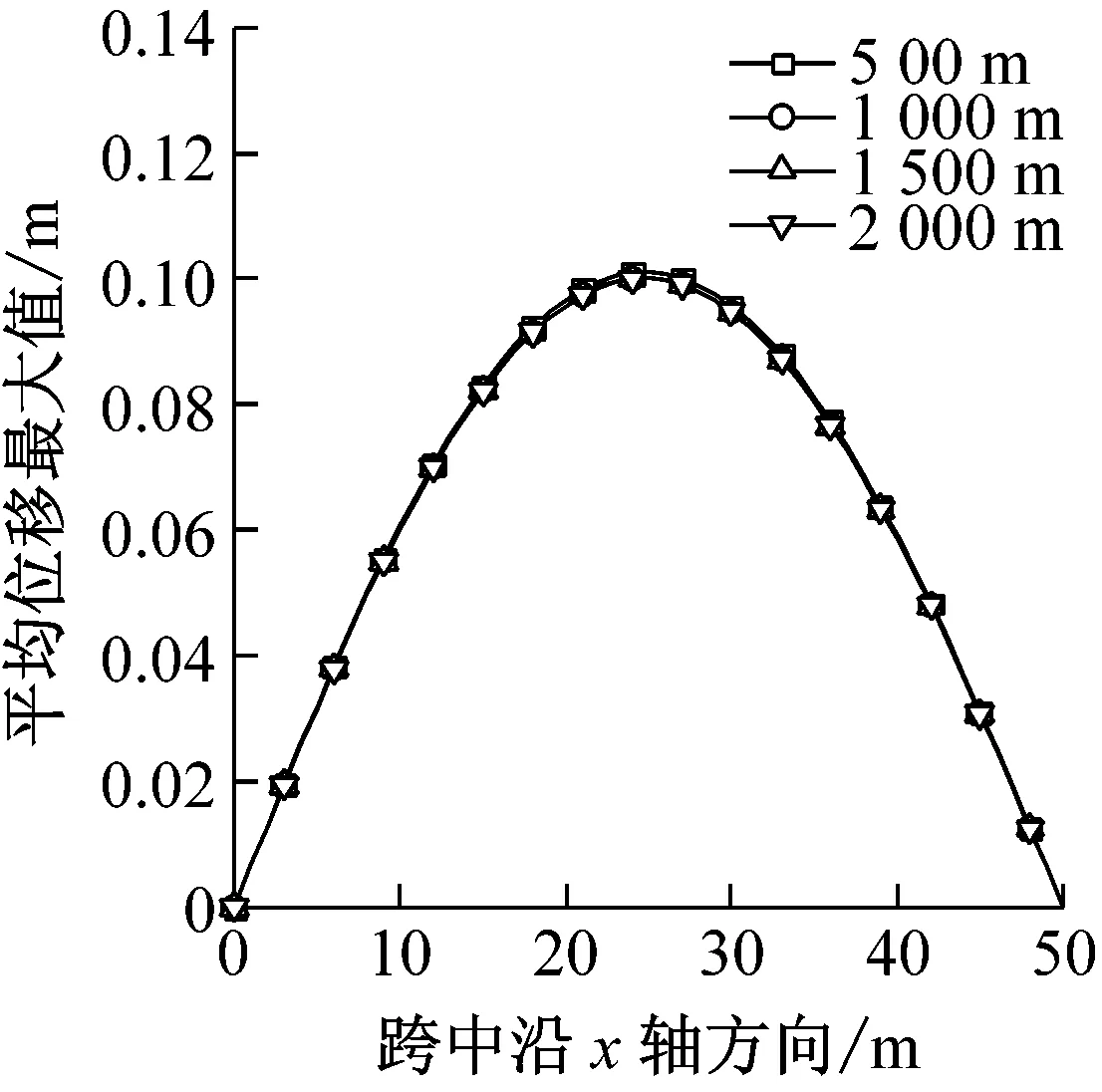
图9给出了最大风速半径rmax分别为500 m、1 000 m、1 500 m、2 000 m时结构的风振响应。由图9可以看出，与移动风速相似，rmax对平均风最大荷载及平均风作用下的最大位移基本上没有影响，而总位移随着rmax的增大而减小，这是因为结构位置在文中假定在离风暴中心3 000 m处，当距离中心超过rmax时，离rmax越近，径向风速波动更加剧烈，荷载波动会变大，整体荷载增大，但是峰值荷载会减小，梁的最大位移减小，且减小幅度也减小。加速度最大值会随着rmax增大先减小后增大，可能是由于半径过大当达到2 500 m时，整体上荷载会变的过大且脉动性增强进而造成加速度的提高，加速度的变化特性造成节点整体荷载风振系数也先减小后增大。

(a)

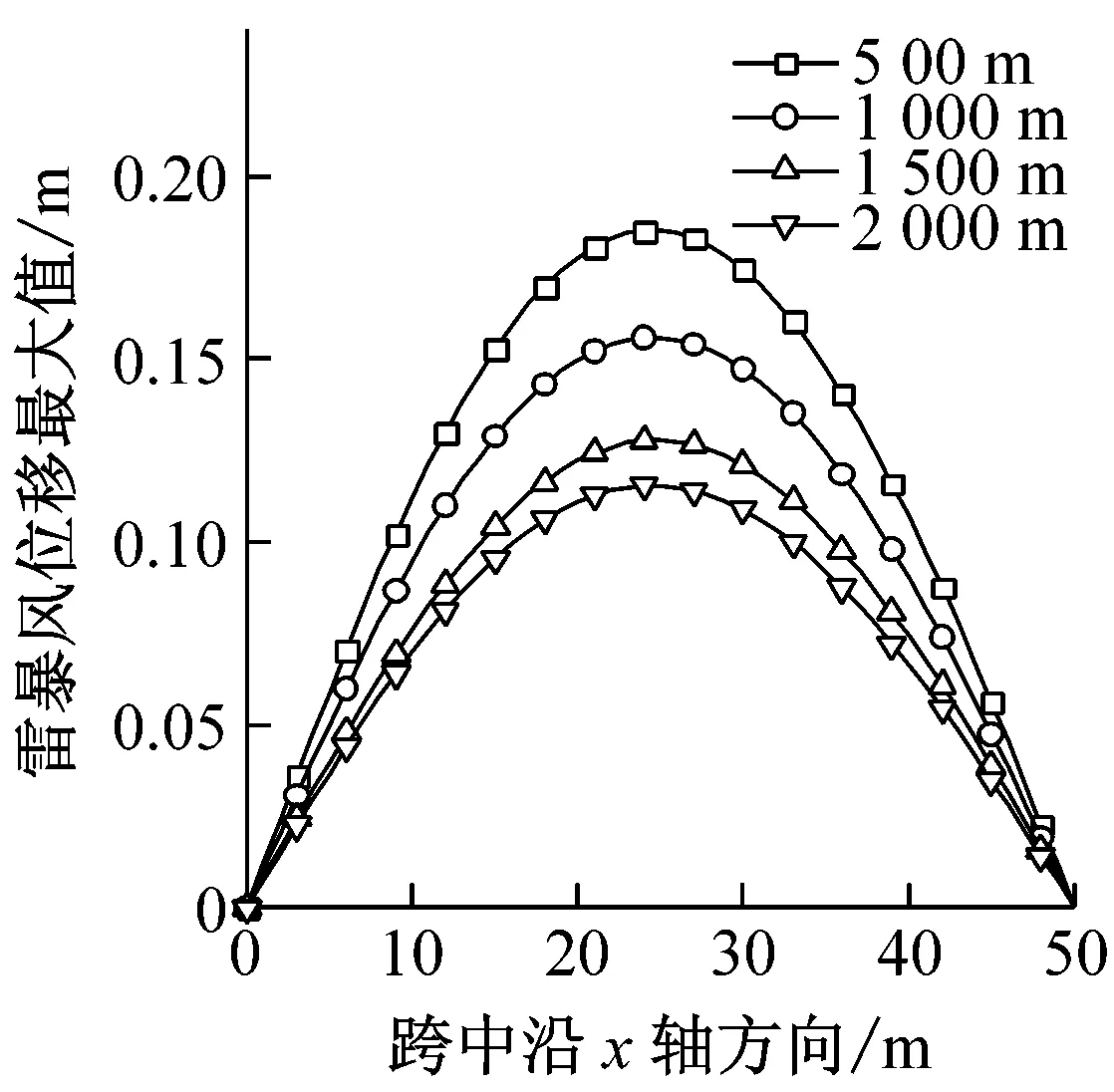
(b)

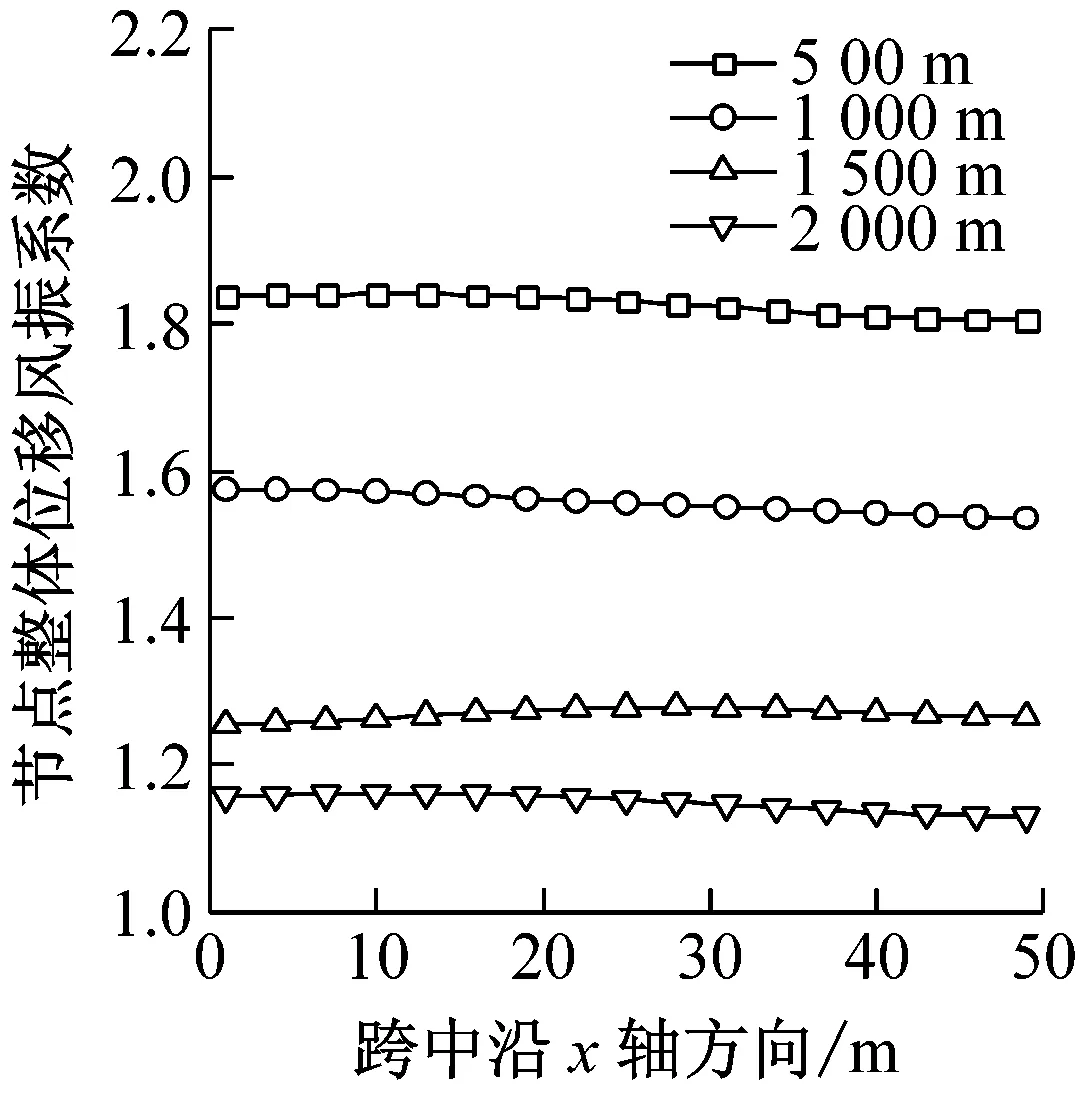
(c)

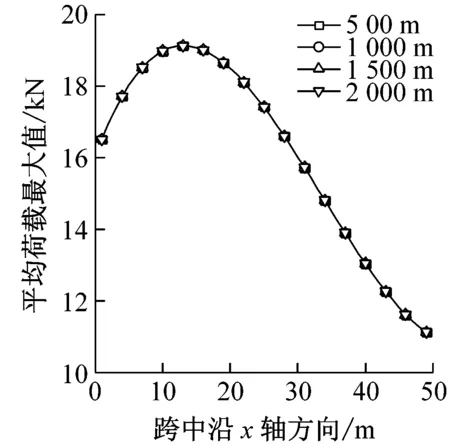
(d)

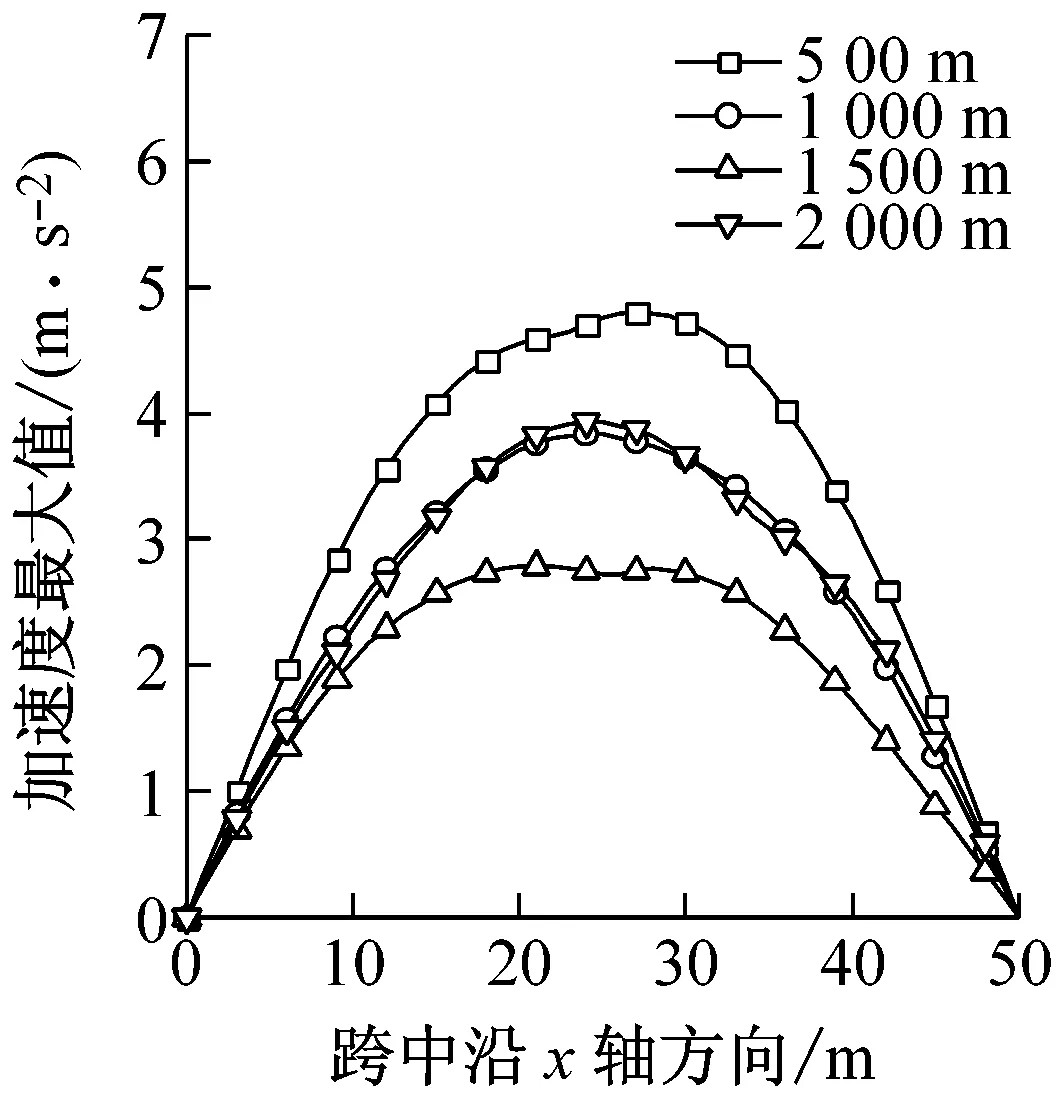
(e)

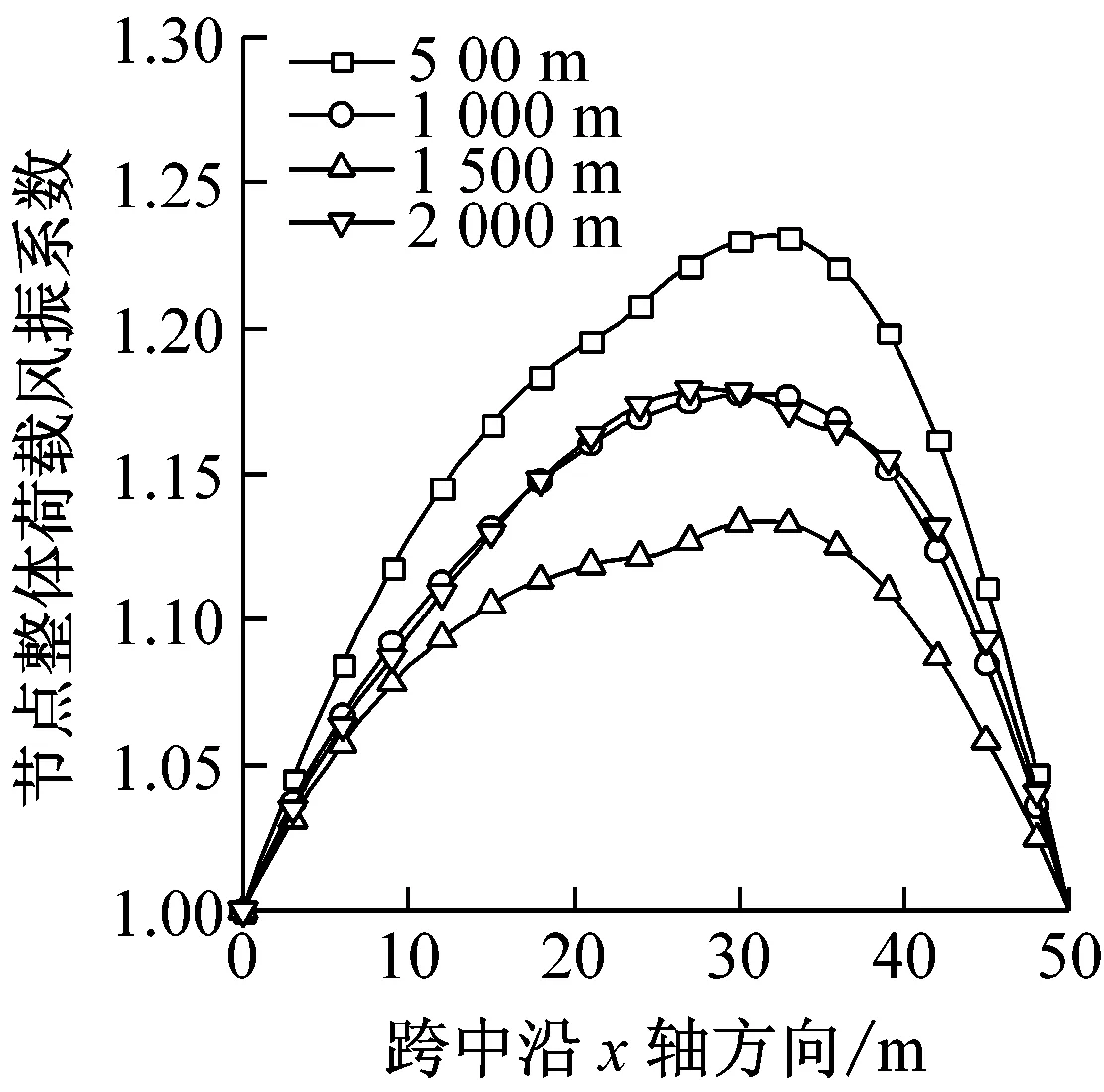
(f)

5 结构整体风振系数比较

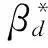
(12)

(13)

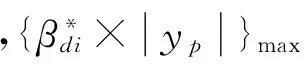
以基准模型为例，按式(12)计算得到的结构整体位移风振系数为1.555，按式(13)计算得到的结构整体荷载风振系数为1.178。分别按整体位移风振系数和整体荷载风振系数对结构的平均风荷载最大值进行放大，获得结构的等效静风荷载，通过静力分析，即可获得等效静风荷载作用下的结构各单元的内力响应。将两种结果与实际响应进行对比，如图10所示。可以看出，无论是位移还是弯矩响应，整体位移风振系数求出的等效静力的响应都与实际情况吻合的较好，除了弯矩对比图中迎风面稍微小于实际位移，其他地方都略大于实际响应。而由整体荷载风振系数求得的则比实际响应要小约25%。可见整体位移风振系数更合理。

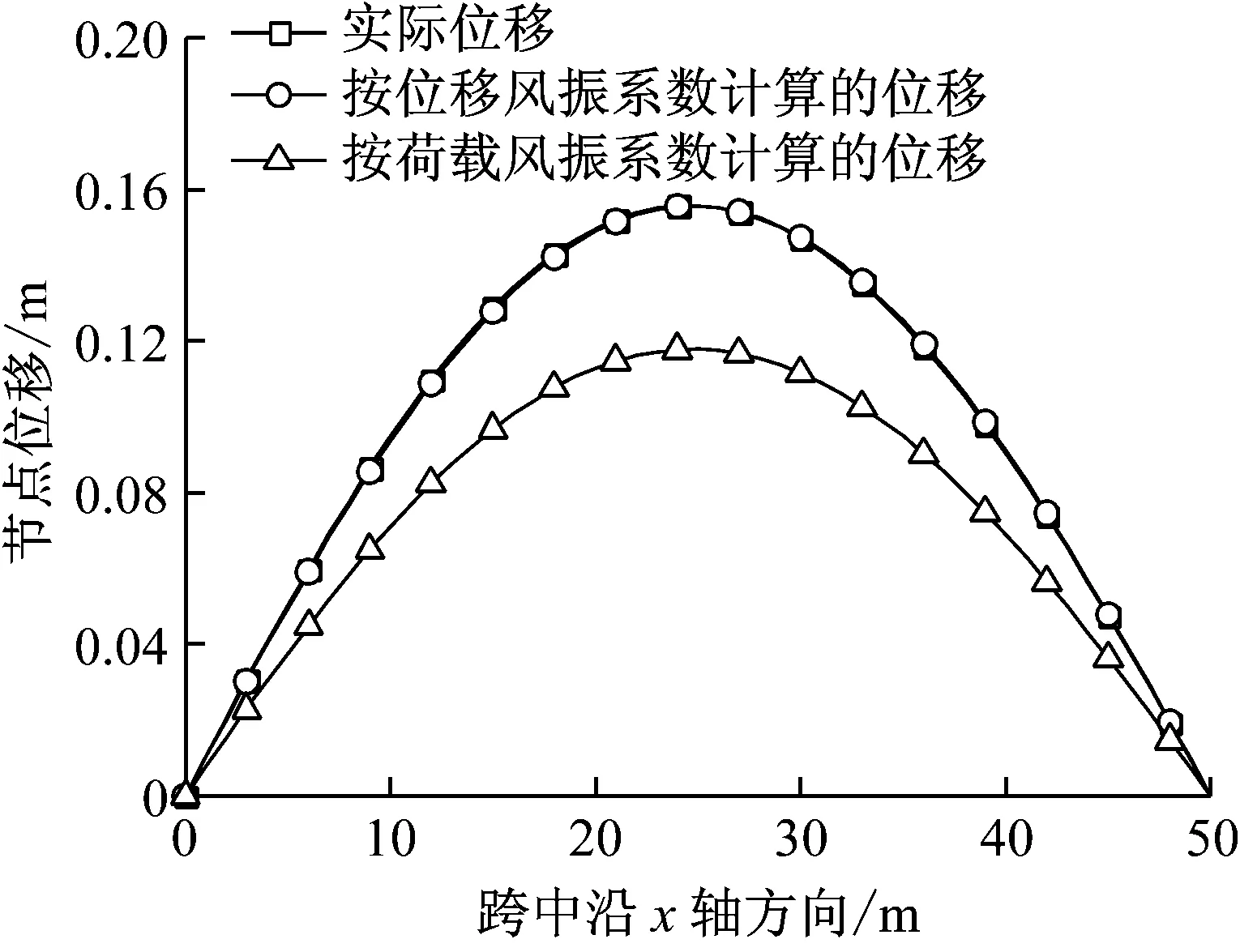
(a) 位移响应比较

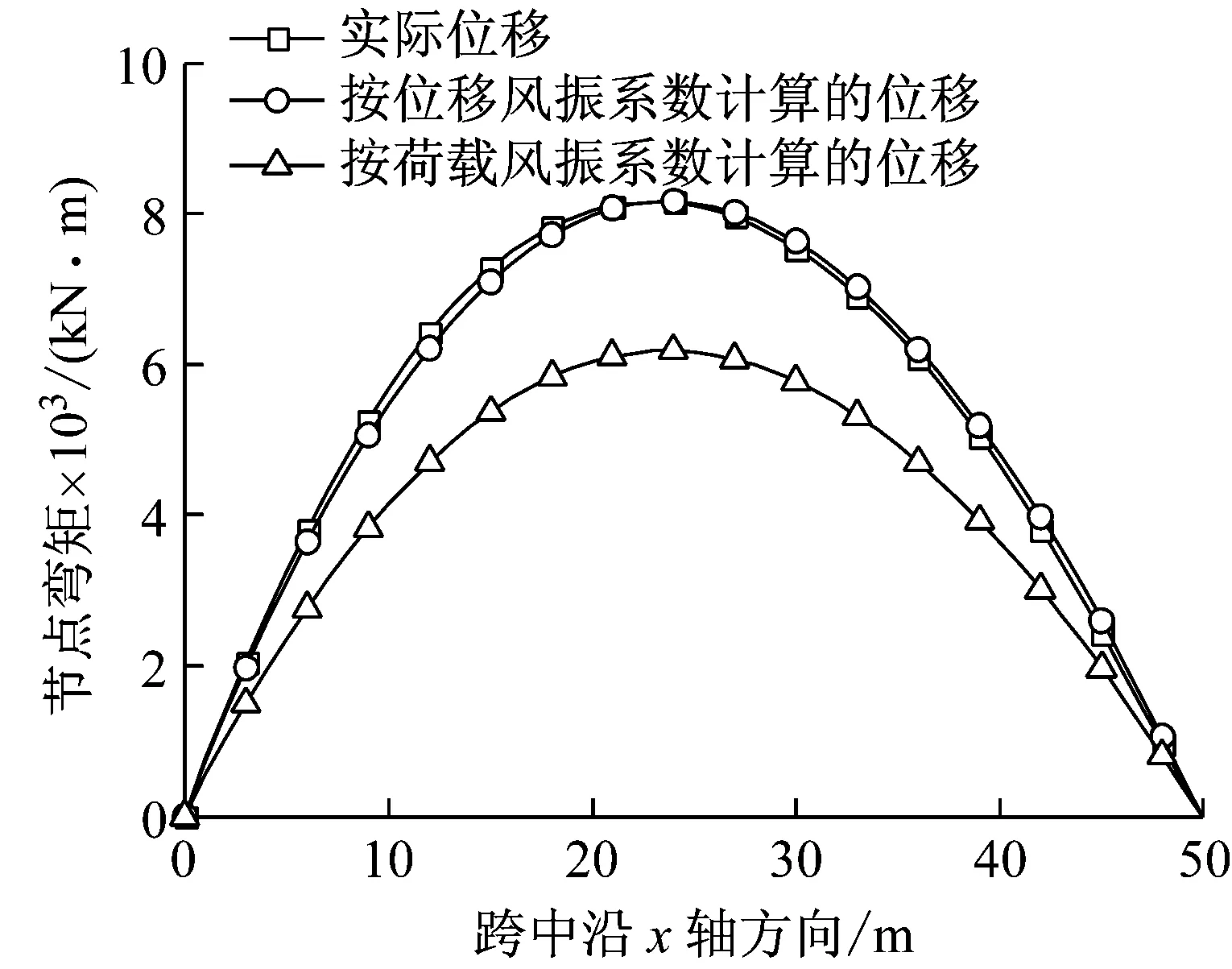
(b) 弯矩响应比较

因此，表1将讨论不同参数下结果整体位移风振系数的计算结果，可以看出高度对系数影响很小，除了线刚度外，其他参数的整体位移风振系数均随之参数的增大而减小，与前面风振响应分析的结果一致。

表1不同参数下的结构整体位移风振系数

Tab.1Thestructuralglobaldisplacementwind-inducedcoefficientofthestructureunderdifferentparameters

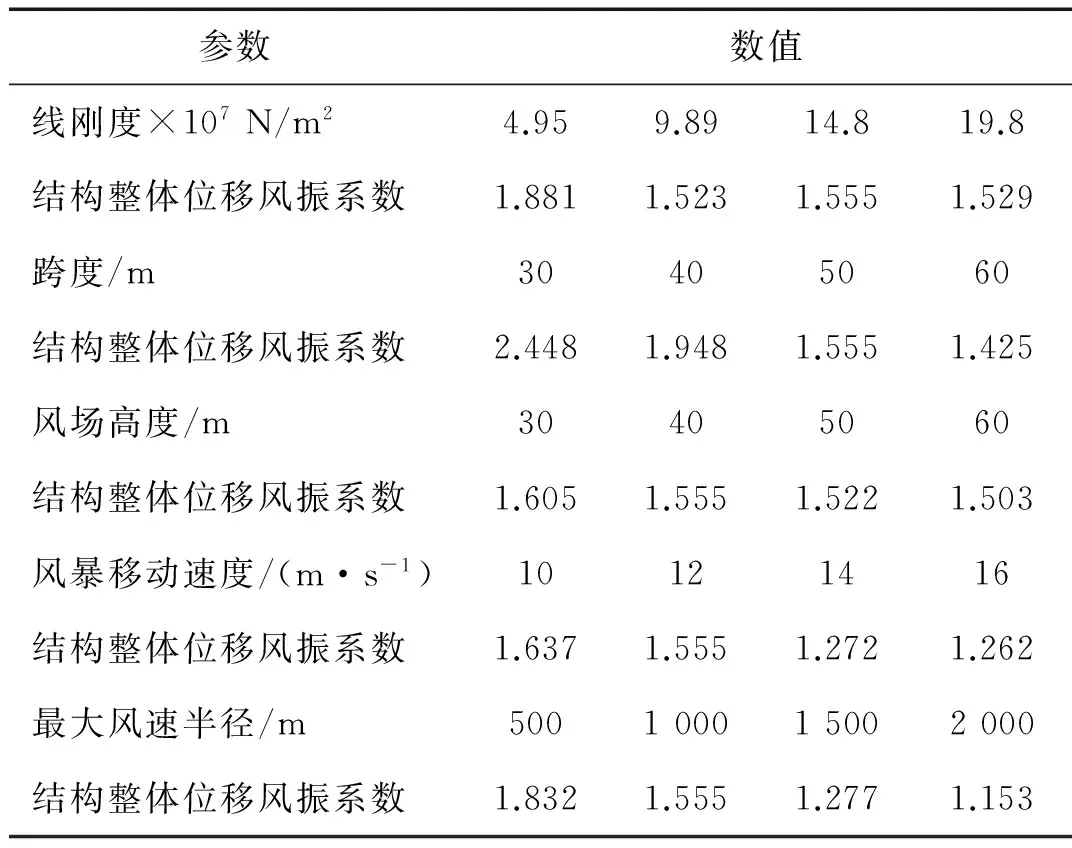
参数数值线刚度×107N/m24.959.8914.819.8结构整体位移风振系数1.8811.5231.5551.529跨度/m30405060结构整体位移风振系数2.4481.9481.5551.425风场高度/m30405060结构整体位移风振系数1.6051.5551.5221.503风暴移动速度/(m·s-1)10121416结构整体位移风振系数1.6371.5551.2721.262最大风速半径/m500100015002000结构整体位移风振系数1.8321.5551.2771.153

6 结 论

(1) 采用Wood竖直风剖面方程与Holmes经验模型模拟平均风场，将脉动风速时程用一随时间变化的幅值调制函数和一个服从标准正态分布的高斯随机过程来模拟具有可行性，AR法模拟精度较高。

(2) 在简支梁力学模型设计参数中，结构在雷暴风作用下的竖向位移会随着跨度和高度的增大而增大；当线刚度、风暴移动速度及最大风速半径的增大时则会减小。对加速度而言、线刚度、高度、风暴移动速度的增大会使之减小，跨度和最大风速半径使之先增大后减小。

(3) 在上述所有情况下，梁上各点的节点整体位移风振系数变化不大，节点所在位置影响较小；而节点所在位置对各节点荷载风振系数有显著影响。随着线刚度的增大，荷载风振系数和位移风振系数均逐渐减小；随着跨度增大，节点整体位移风振系数随之减小，但节点整体荷载风振系数的先增大后减小；高度对它的节点整体风振系数影响不大；移动速度和最大风速半径增大会减小节点整体位移风振系数，而使整体荷载风振系数先减小后增大。

(4) 基于结构整体位移风振系数求出的等效静力响应与实际情况吻合较好，而由结构整体荷载风振系数求得的则比实际响应小约25%，因此采用结构整体位移风振系数分析雷暴风等效静风响应更为合理。

[1] 罗楠，廖海黎，李明水. 大跨屋盖时域多目标等效静力风荷载计算方法[J]. 工程力学, 2013(4): 316-321.

LUO Nan,LIAO Haili,LI Mingshui.Universal equivalent static wind loads for long-span roofs in time domain[J]. Engineering Mechanics,2013(4): 316-321.

[2] BENOWITZ B A,DEODATIS G. Simulation of wind velocities on long span structures: A novel stochastic wave based model[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015,147: 154-163.

[3] 李玉学，杨庆山，田玉基,等. 大跨屋盖结构风致背景响应和共振响应实用组合方法[J].振动与冲击, 2014, 33(19): 199-205.

LI Yuxue,YANG Qingshan,TIAN Yuji,et al. Practical combination method for wind-induced backgroundresponse and resonant response of large span roofs[J]. Journal of Vibration and Shock, 2014, 33(19): 199-205.

[4] 潘峰. 大跨度屋盖结构随机风致振动响应精细化研究[D].杭州: 浙江大学, 2008.

[5] BAI Linjia,ZHANG Yunfeng. Nonlinear dynamic behavior of steel framed roof structure with self-centering members under extreme transient wind load[J]. Engineering Structures, 2013, 49: 819-830.

[6] FUJITA T T. Downburst: microburst and macroburst[M]. University of Chicago Press, 1985.

[7] 陈勇，崔碧琪，彭志伟,等. 球壳型屋盖在冲击风作用下的抗风设计参数及CFD分析[J]. 空气动力学学报, 2012(4): 456-463.

CHEN Yong，CUI Biqi，PENG Zhiwei. Wind-resistant design parameters and CFD analysis of spherical roofsubjected to thunderstorm downbursts[J].Acta Aerodynamica Sinica,2012(4): 456-463.

[8] 陈勇，柳国光，徐挺, 等. 运动雷暴冲击风水平风速时程分析及现象模型[J]. 同济大学学报(自然科学版), 2012, 40(1): 22-26, 44.

CHEN Yong，LIU Guoguang，XU Ting.Time histories of horizontal wind velocity of moving thunderstorms and pheno-menological model[J].Journal of Tongji University (Natural Science),2012, 40(1): 22-26, 44.

[9] CHEN L Z,LETCHFORD CHRIS W. A deterministic-stochastic hybrid model of downbursts and its impact on a cantilevered structure[J]. Engineering Structures, 2004, 26(5): 619-629.

[10] 楼文娟，王嘉伟，吕中宾, 等. 运动雷暴冲击风作用下输电线路风偏的计算方法[J].中国电机工程学报, 2015(17): 4539-4547.

LOU Wenjuan, WANG Jiawei, LÜ Zhongbin. Calculation method of wind-induced oscillation of tansmissionline under moving downburst[J].Proceedings of the CSEE,2015(17): 4539-4547.

[11] CHEN L,LETCHFORD C W. Numerical simulation of extreme winds from thunderstorm downbursts[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(9/10/11): 977-990.

[12] HOU Jingpeng, SUN Zitang,LI Yanxia. Simulation of turbulent wind velocity for transmission tower based on auto-regressive model method[J]. Energy Procedia, 2012, 17: 1043-1049.

[13] LETCHFORD C W,CHAY M T. Pressure distributions on a cube in a simulated thunderstorm downburst. Part B: moving downburst observations[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(7): 733-753.

[14] 周臻，孟少平，吴京. 预应力双层柱面网壳的风振响应与整体风振系数研究[J]. 工程力学, 2011(10): 124-132.

ZHOU Zhen,MENG Shaoping,WU jing. The wind-induced response and global wind vibration coefficient of prestressed double-layer cylindrical reticulated shells[J]. Engineering Mechanics, 2011(10): 124-132.

Parametricanalysisforasimplysupportedbeamroofstructure’swind-inducedvibrationresponseunderdownburst

ZHOU Zhen, DING Huimin, KONG Xiangyu

(Key Laboratory of Concrete and Prestressed Concrete Structures of the Ministry of Education, Southeast University, Nanjing 210096, China)

Based on the time-domain analysis method, the wind-induced vibration response of a simple supported beam roof structure under downburst was studied with the parametric analysis method. Here, a hybrid stochastic model was chosen to simulate the strong wind load of downburst, the mean wind speed was simulated using Wood vertical wind profile equation and Holmes’ empirical model, the fluctuating wind speed was simulated using AR model based on Kaimal target spectrum. Spectral analysis results showed that the simulated results of downburst have a better accuracy. The influences of the main structure’s parameters and downburst parameters on the structure’s wind-induced vibration response were analyzed. The results showed that the structure’s stiffness and span, the maximum wind speed radius and downburst moving velocity have larger influences on the structure’s wind-induced vibration response. Aiming at the time-varying feature of both the mean wind speed and the fluctuating wind speed, the global wind-induced vibration coefficient calculation method was adopted based on the envelope concept, the global displacement wind-induced vibration coefficient and the global load one were studied under different parameters, respectively. The results showed that adopting the structure’s global displacement wind-induced vibration coefficient to compute the equivalent static wind load for downburst has a higher accuracy.

downburst; hybrid stochastic model; parametric analysis; wind-induced vibration coefficient

国家自然科学基金(51208095);江苏省“青蓝工程”；江苏省六大人才高峰(JZ-002)

2016-05-13 修改稿收到日期：2016-07-13

周臻 男，博士，教授，1981年9月生

TU323.3

： A

10.13465/j.cnki.jvs.2017.17.027