内外压分别作用下冷却塔风振系数对比研究*

杜凌云， 柯世堂， 侯宪安

(1.南京航空航天大学土木工程系 南京，210016) (2.远景能源(江苏)有限公司 上海,200050) (3．中国电力工程顾问集团西北电力设计院土木工程技术部 西安，710075)

引 言

为了适应火/核电产业的迅速发展趋势，超过现行规范[1]190m高度限值的超大型冷却塔陆续兴建，相比常规冷却塔其阻尼更小、柔度更大，因此风振动力放大效应尤为显著。已有研究[2-3]表明，冷却塔内表面风压脉动幅值不容忽视，而现有结构稳定性验算及荷载组合中均直接以规范成塔单一外荷载风振系数1.9计入内表面风荷载的动力放大作用，并不能真实反映内压风振系数的三维分布模式。此外，国内外冷却塔规范[1,4-7]及相关研究[8-14]均缺乏对内压风振系数的探讨和规定，因此对比探讨内、外压作用下此类超大型冷却塔的风振系数分布特性和精细化取值具有重要的理论和工程意义。

针对大型冷却塔风振系数研究，文献[8]通过一致耦合法对比分析了某核电超大塔的风振系数取值与分布特征，发现风振系数在塔底和喉部背风区域出现峰值。文献[9-10]基于时域法和虚拟激励法对超大冷却塔进行风振响应计算，结果表明位移风振系数在塔筒中部最小，分别向塔顶和塔底逐渐增大。文献[11]针对双塔布置与周边山地环境下冷却塔的动态响应进行分析，得知山地和群塔干扰均使结构风振系数增大。文献[12-14]基于气弹测振风洞试验研究了不同高度和塔型大型冷却塔三维风振系数分布特性，获得了一些对设计有指导意义的结论。然而，已有的研究成果均针对冷却塔外压作用下的风振系数，忽略了内压作用引起的风振效应和风振系数差异化取值影响，更缺乏对不同等效目标下内压风振系数的对比研究，这也成为现有超大型冷却塔风荷载精细化取值与降低施工成本的制约因素。

鉴于此，以国内某在建210m高间接空冷冷却塔为研究对象，通过刚体同步测压风洞试验分别获取冷却塔内、外表面脉动风压时程，并将外压曲线与国内外相关规范进行对比以验证试验结果的可靠度。基于塔筒-支柱-环基一体化有限元模型对超大型冷却塔进行内、外压分别作用下的时域动力计算，对比研究塔筒径向位移、子午向轴力、Von Mises应力和环向弯矩4种典型目标响应下的一维、二维和三维内、外压风振系数分布模式，给出了内、外压作用下风振系数的取值建议与二维拟合公式。

1 工程简介

本试验结构原型采用内陆某在建大型间接空冷塔，塔高为210m，喉部标高为157.5m，中面直径为110.37m，进风口标高为32.5m，塔底直径为180m。塔筒分段等厚，最大厚度为2m，最小厚度为0.37m。表1具体列出了该工程冷却塔结构的主要结构尺寸。

2 风洞试验与结果分析

2.1 刚体测压风洞试验

测压试验所用风洞为大气边界层闭口回流式5.0 m×4.5 m矩形截面风洞，刚体模型按1∶400缩尺比制作，外压试验在塔筒外表面沿子午向和环向布置12×36=432个测点，内压试验在塔筒内表面布置10×20=200个测点，图1给出了试验模型内、外压测点布置示意图，内、外压以30%透风率考虑百叶窗工作开启状态[3]。

地面粗糙元置于来流前部用以模拟B类地貌的大气边界层风场，风速与湍流度剖面如图2所示，由图可见风场模拟效果较好。由于物理风洞的局限性，需要通过调整试验风速和改变表面粗糙度的方法来补偿模型缩尺导致的雷诺数不匹配问题。通过比较知道，采用表面贴粗糙纸带(沿圆周均匀分布二、三间隔宽5mm，计36条竖向通长粗糙纸带)和来流风速10m/s手段模拟效果最好。图3将冷却塔喉部断面外表面体型系数与规范推荐曲线进行对比(其中体型系数为无量纲单位)，可知试验曲线与各国规范趋势较为吻合，数值与中国水工规范[1]最为接近。

图1 刚体测压模型内、外压测点布置示意图Fig.1 Layout diagram of wind pressure model internal and external pressure measuring point

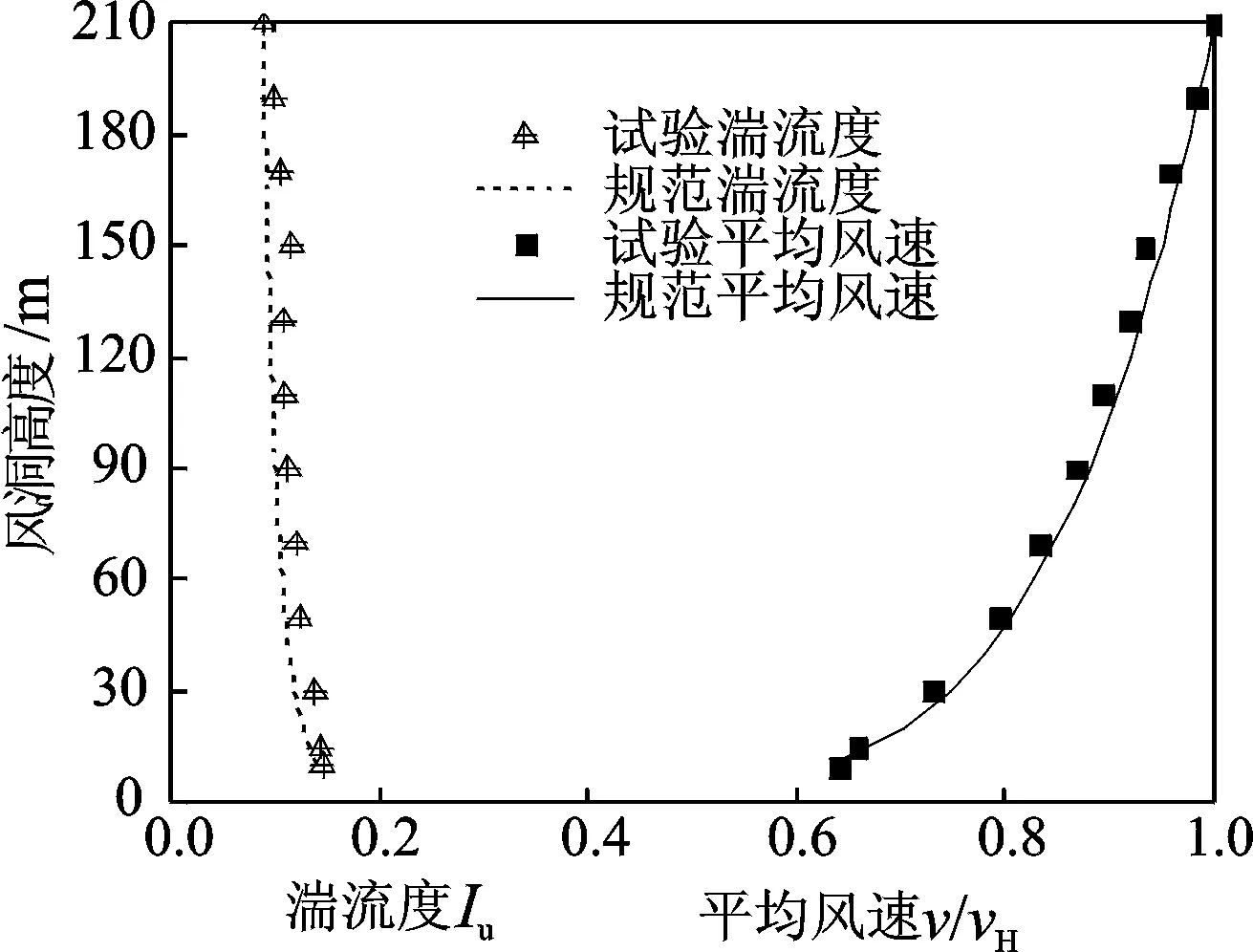
图2 平均风速和湍流度剖面Fig.2 Profiles of mean velocity and turbulence intensity

图3 雷诺数效应模拟体型系数与规范对比曲线Fig.3 The simulation of reynolds number effect results

2.2 结果分析

图4给出了内、外表面体型系数均值在子午向0～50m，50～100m，100～150m和150～210m高度区间内随环向角度变化的对比曲线。分析可知：

图4 内、外表面不同高度体型系数均值对比曲线Fig.4 Mean shape factor of internal and external surface at different height range

1) 内表面体型系数均值沿环向和子午向分布并未呈现出单一分布，三维特征显著；

2) 0～50m高度区域内体型系数沿环向分布相对其他区域较不均匀，来流经百叶窗进入塔筒内部，在至塔筒背风区域内表面附着流动上升，导致其风压绝对值显著减小；

3) 50～100m，100～150m和150～210m高度区域内表面体型系数沿环向角度变化平缓，其值分别在-0.35，-0.30与-0.35左右波动；

4) 4个高度区域在塔筒迎风面分布曲线较为吻合，到达负压极值区后50～100m和150～210m高度区域外表面体型系数值明显增大，背风面风压平台处数值相对其他高度区间略大。

图5给出了内、外表面体型系数均方根在子午向0～50m，50～100m，100～150m和150～210m高度区间内随环向角度变化的对比曲线。

对比得出：内表面体型系数脉动值沿环向分布比较均匀，但受塔顶出风口气流的影响，塔筒上部内表面体型系数脉动较大；0～50m和150～210m高度区间外表面体型系数脉动值沿环向角度分布较为吻合，50～100m和100～150m分布趋势相似，在迎风面与侧风面体型系数脉动值相对塔筒下部和上部偏离较大，最大为40.96%。

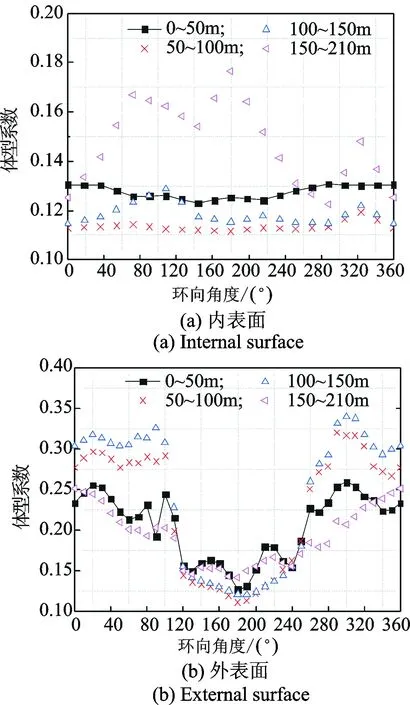
图5 内、外表面不同高度体型系数均方根对比曲线Fig.5 Root mean square shape factor of internal and external surface at different height rangek

3 风振系数对比分析

3.1 自振特性分析

基于有限元软件ANSYS建立仿真分析模型，塔筒、支柱和环基、弹性地基分别采用空间壳单元、梁单元以及弹簧单元，共计29 640个，环基与塔筒和支柱分别通过多点约束耦合和刚性域进行连接。采用分块Lonczos法[15]进行动力特性计算，表2给出了典型阶模态信息。分析可知：突破性塔高使得结构基频低于普通冷却塔，降至0.58Hz，柔性更强；频率分布相对密集，振型多变，具有不固定的环向和竖向谐波；整体结构在30阶发生倾覆，此时自振频率增幅较大。

表2 冷却塔结构典型阶振型信息

3.2 计算参数定义

该冷却塔位于B类地貌，100年一遇最大风速为23.7m/s，结构阻尼比取为规范值[16]5%。将风洞试验获取的冷却塔内、外表面风压时程分别输入有限元模型结构体系，采用完全瞬态法进行风致动力特性分析，并选择4种响应等效目标进行节点风振系数计算，如表3所示。响应风振系数计算公式[17]为

(1)

表3 响应等效目标分类

3.3 三维风振系数

图6～9给出了内、外压作用下以A，B，C和D为响应目标的风振系数三维分布图(其中风振系数为无量纲单位)。由图可知：塔筒表面节点风振系数沿环向和子午向差异显著，内、外压作用下分别以等效目标D下的风振系数分布最为均匀，其他3种等效目标局部节点风振系数失真较为严重；外压作用下节点风振系数分布相对内压作用波动较为显著，且失真主要发生于背风面，而内压作用下风振系数失真区域主要集中在塔底和塔顶部位。

图6 内、外压作用下响应目标A节点风振系数三维分布示意图Fig.6 The three-dimensional distribution of node wind vibration coefficient under A response target

图7 内、外压作用下响应目标B节点风振系数三维分布示意图Fig.7 The three-dimensional distribution of node wind vibration coefficient under B response target

图8 内、外压作用下响应目标C节点风振系数三维分布示意图Fig.8 The three-dimensional distribution of node wind vibration coefficient under C response target

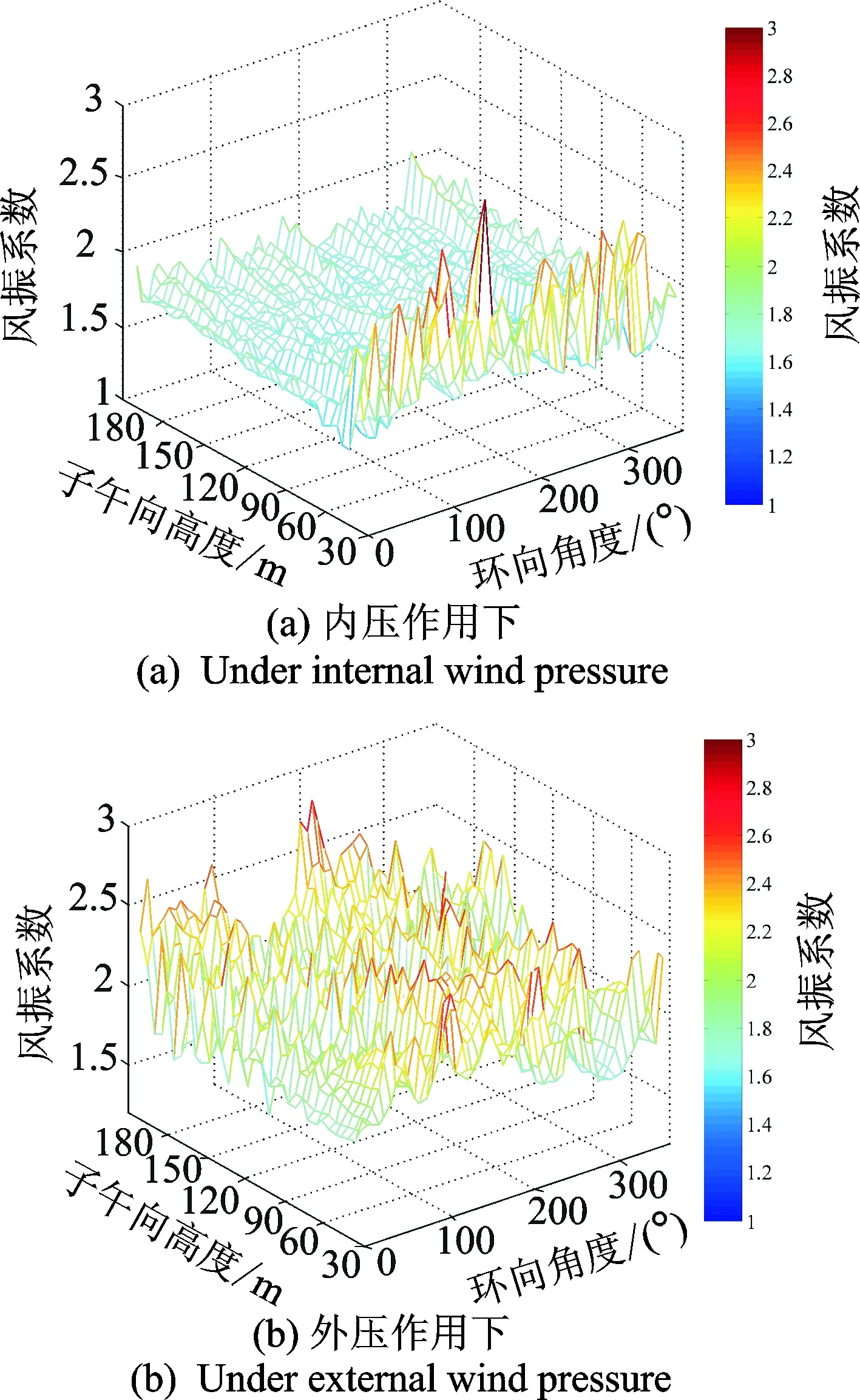
图9 内、外压作用下响应目标D节点风振系数三维分布示意图Fig.9 The three-dimensional distribution of node wind vibration coefficient under D response target

3.4 二维子午向风振系数

分别采用0°子午线和平均响应绝对值的最大值(分别简称为等效目标1和2)两种取值等效目标计算不同响应等效目标下的冷却塔结构二维子午向风振系数，如图10所示。对比分析可得，以取值等效目标2为依据选定二维子午向风振系数的数值范围相对较为合理，等效目标1下的风振系数值和趋势均波动较大。综合比较可得，内压作用下的塔筒二维子午向风振系数相比外压作用下数值较小，且层风振系数沿子午向高度波动较小。

3.5 二维环向风振系数

将塔体沿子午向划分为0～50m，50～100m，100～150m和150～210m4个区域，研究二维风振系数沿环向角度变化规律，如图11所示，给出了响应目标A，B，C和D下的不同高度区域二维环向风振系数分布曲线。对比分析表明：a.外压作用下塔筒二维环向风振系数与内压作用下相比较大，除响应目标A外，内压作用下风振系数沿环向角度分布更为稳定；b.塔筒下部和上部受进风口和出风口气流影响使得沿环向出现较大风振系数，塔筒中部风振系数沿环向分布趋势较为平稳；c.以响应目标A作为风振系数取值标准可能导致失真风振系数范围较大，推荐以规范规定的子午向轴力和平稳分布的Mises应力两个响应目标下的风振系数作为冷却塔结构真实风振系数参考依据。

图10 内、外压作用下不同响应目标二维子午向风振系数分布曲线示意图Fig.10 Thedistribution of two-dimensional meridional wind vibration coefficient under different response targets

图11 不同响应目标下不同高度断面二维环向风振系数分布曲线示意图Fig.11 The distribution of two-dimensional ring wind vibration coefficient under different response targets

3.6 风振系数二维拟合公式

以子午向高度比为变量，拟合给出内、外压作用下冷却塔风振系数估算公式，如式(2)所示，其系数取值见表4

β(h)=a1sin(b1h+c1)+a2sin(b2h+c2)+

a3sin(b3h+c3)+a4sin(b4h+c4)+

a5sin(b5h+c5)

(2)

将内、外压风振系数拟合曲线与计算值进行对比，见图12。由图可见：拟合效果相对较好，但塔底和塔顶风振系数失真，与拟合曲线吻合较差；内压风振系数小于外压风振系，且沿高度分布较为稳定。

图12 内、外压风振系数计算值与拟合曲线对比示意图Fig.12 Internal and external wind vibration coefficient of fitted and caculated values

Tab. 4 Parameters of internal surface shape coefficient of cone and cylinder section

aibiciaibici110.6502.240.443.842.60-0.4029.0302.473.4710.404.921.1030.01014.56-2.258.235.164.0640.01022.49-2.4900050.00432.74-6.40000

3.7 整体风振系数

基于上述三维、二维子午向以及二维环向风振系数计算结果，给出内、外压作用下以4种响应为目标的结构整体风振系数建议取值，如表5所示。由表可知，不同等效目标下内压整体风振系数均小于外荷载整体风振系数，且以响应目标B和D均值作为整体风振系数推荐取值，分别为1.69和1.89，小于规范风振系数1.9。

表5 整体风振系数取值建议

Tab.5 The recommended values of overall wind vibration coefficient

A1.892.01B1.691.99C1.731.86D1.691.781.691.89

4 结束语

系统研究了内、外压分别作用下超大型冷却塔风振系数一维、二维与三维分布特性，主要涉及风洞试验、动力特性分析、风振响应计算、参数分析和公式拟合等内容。结果表明，内表面体型系数三维分布特征显著，其脉动性相对外压较小但不可忽略，采用真实内压风振系数更能精确反映冷却塔内压引起的风振效应。本研究采用的风洞试验方法与完全瞬态算法可有效解决冷却塔内压风振系数取值问题。外压作用下的风振系数相比内压风振系数波动较强且数值较大，内、外压分别作用下整体风振系数均小于规范B类地貌推荐取值，建议取为1.69和1.89。