涡轮机叶片同步振动参数辨识方法研究(实验研究)

王维民， 任三群， 陈立芳, 邵化金

(北京化工大学 高端机械装备健康监控与治愈化北京市重点实验室, 北京 100029)

涡轮机叶片同步振动参数辨识方法研究(实验研究)

王维民， 任三群， 陈立芳, 邵化金

(北京化工大学 高端机械装备健康监控与治愈化北京市重点实验室, 北京 100029)

为满足工程应用环境中用尽可能少的传感器和更紧凑的安装空间中实现叶片振动的精确测量，在叶尖定时测量方法的基础上，提出并实验研究了基于变速扫频拟合和辅助参数全局自回归法(GARIV法)相结合来辨识叶片同步振动时的振动参数。建立了高速直叶片实验台(最高转速45 000 r/min, 叶尖线速度322.8 m/s)。在实验研究过程中，完成了叶片同步振动的参数辨识(中心频率、振动最大幅值、相位、振动恒偏量和倍频值)，准确绘制出安装6个磁铁激励下的叶片部分振动坎贝尔图。同时对不同激励个数时叶片部分谐振动做了实验研究和分析。通过对比叶片的预应力模态计算结果和实验辨识结果， 两者偏差小于6%。该方法可为叶片故障预警、动应力非接触测量提供技术途径。

叶尖定时； GARIV法； 同步振动； 参数辨识

叶片作为涡轮机的核心部件，监测其运行状况具有重要意义。叶片振动参数是其运转健康状态的重要指标，通过对机器启动和运行中的振动参数(频率、幅值、相位)进行监测，可以进行健康状态的评价。近年来，叶片振动监测的方法受到广泛关注[1]。

叶片同步振动参数辨识领域对辨识算法的研究已久，但在实际工程应用中使用的较少，一方面是由于辨识方法受干扰影响较大，很难获得准确的辨识结果[2-3]；另一方面，传感器的使用个数和排列方式也是很重要的制约因素[4-5]。在综合了扫频遍历法[6]在叶片同步振动时谐共振处的振动幅值和频率等振动参数的拟合精度较高的优点；同时为了减少传感器的使用数量，在叶片同步振动中存在的振动倍频值的求取上采用GARIV法[7-8]。上述方法的结合可在传感器使用的数量上减少到4支，安装的位置较为紧密，且可以获得较高的参数辨识精度。在实验研究之前已经通过建模仿真对上述方法进行了验证，并且确定了叶片同步振动参数辨识的测试方案。

本文针对实验测量确定了振动参数辨识流程，通过综合比较已开发出的不同激励方式的叶片振动测量实验台[9-12]，建立了磁铁激励式的高速直叶片实验台。通过实验台完成了不同激励个数下的叶片同步振动参数辨识，测量结果与理论建模获得结果相差较小。通过实验验证的方式确定该方法在实际测量中是有效可行的。

1 叶片同步振动参数辨识流程

在同步振动参数辨识及叶片实验台具体操作过程中，需对传感器安装位置进行确定，同时对于测量方案也应进行确定。基于扫频拟合和GARIV法的叶片同步振动参数辨识流程如图1所示。

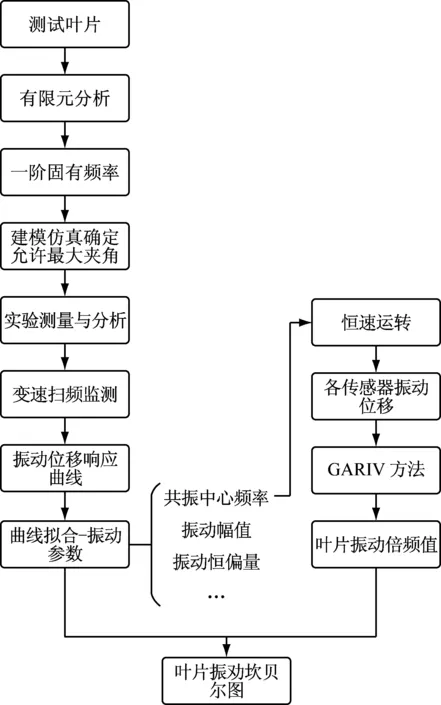
图1 叶片同步振动参数辨识流程图

对于传感器安装位置确定上，首先通过对实验用到的叶片进行有限元分析获得叶片的一阶固有频率，该频率值可用于估计叶片可能存在的最大倍频值，进而确定合适的传感器夹角。

关于具体的测量过程需要按步骤依次进行。首先需要通过变速扫频监测叶片的振动位移随转频之间的变化情况，进而确定发生的叶片同步振动区间。截取不同传感器对应的同一编号叶片的谐共振区域分别进行参数拟合，进而获得叶片同步振动参数，如谐共振中心频率、振动幅值，振动恒偏量等。

然后根据存在的谐共振中心频率选取合适的运转转速进行恒速运转，四支传感器监测的振动位移经过GARIV法分析获得振动倍频值，进而确定存在的不同谐共振区对应的振动倍频值。在实验过程中电机转速会存在一定的转速波动，当运转频率与谐共振中心频率一致时，叶片振动位移可能会随转速波动产生较大的波动。故在实际测量中将运转频率值设定在谐共振中心频率值附近。

最后可根据拟合获得的谐共振中心频率、振动幅值等参数，结合谐共振对应的振动倍频值做出叶片振动坎贝尔图。

2 实验装置

2.1实验台结构

实验中使用了高速直叶片振动实验台，具体细节和整体概貌如图2所示。高速直叶片振动监测实验台主要由底座、支撑体(电机)、操作平台、测试轮盘、护罩、永磁激励部件及其他辅助元部件组成。实验台底座借助T型槽用螺栓与基座相连，包裹着电机的支撑体通过周向均布的三个螺钉与底座实现紧固。测试轮盘外安装兼做传感器支架的护罩，护罩周向开有呈特定角度(最小6°)的若干个传感器安装孔，顶端设有键相传感器(通过磁座固定在操作平台上)安装孔。护罩顶部开有12个永磁激励部件安装孔。每一个激励部件都内嵌一个钴基永磁铁，用以提供激振力，通过调整部件数量及分布情况，可开展若干组合下的激励测试实验。

图2 高速直叶片实验台

2.2实验台测试系统

测试系统中采用5通道激光源(1通道用于键相、4通道用于叶尖计时)，光功率可在0～1 W之间连续调节。使用独立供电的光电转换器，最大支持带宽为150 MHz。采用基于FPGA的高速数据采集系统Compact RIO，可实现20MS/s的数字采样。传感器安装及测试系统见图3。

2.3测试轮盘的结构振动特性

本实验台叶轮的剖视图如图4(a)所示，该叶轮通过锥面定位安装在电机轴上。为了降低叶片的固有频率从而使得在更低的转速下激起高阶的固有频率，在叶片根部进行叶片局部减薄，结构如图4(b)，最小厚度1.5 mm。轮盘俯视图如图4(c)所示，整个轮盘由32个叶片组成，轮盘直径138 mm，叶尖厚度3 mm。在轮盘上部开有键相槽和为了平衡键相而设计的平衡槽。用ANSYS软件对其模态进行分析，得到的一阶一节径模态如图4(d)所示，一阶振动频率为2 140.3 Hz(转速为7 000 r/min时的预应力模态)。

图3 传感器安装及测试系统

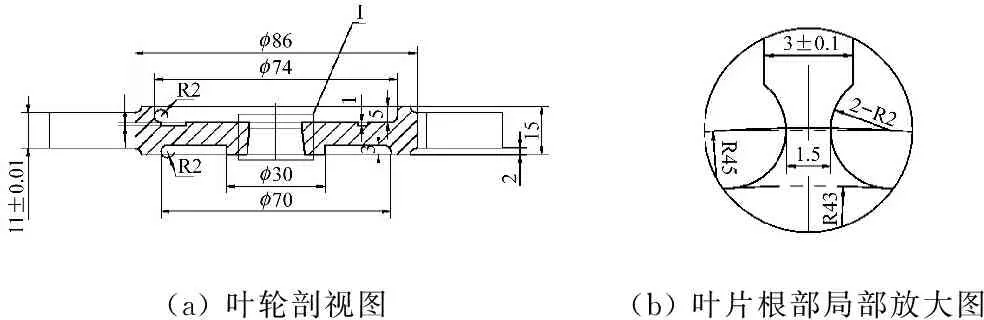
(a)叶轮剖视图(b)叶片根部局部放大图

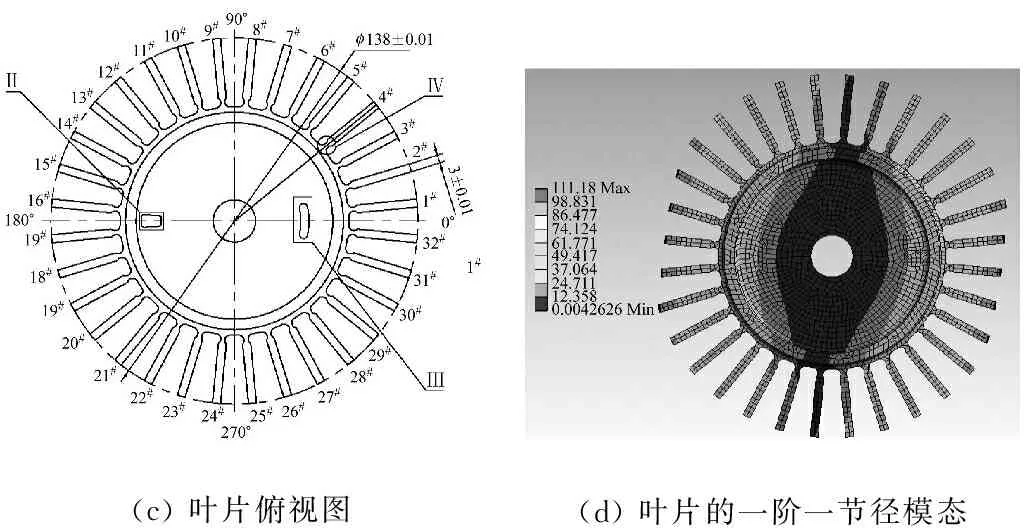
(c)叶片俯视图(d)叶片的一阶一节径模态

图4 叶轮的结构及一节径模态

Fig.4 The impeller structure and first order mode

3 实验与结果分析

实验测量与建模仿真之间有着很大的差距，如在建模仿真中可以获得较为准确的叶片振动位移值，但在实际的测量过程中，叶片的振动位移需要通过叶尖定时测量来获得。已知叶尖定时测量最重要的是获得实际到达叶顶传感器的时间与理论到达传感器的时间差值来求取叶片振动位移。

但实际测量过程中理论到达时间的确定是非常难的，已知的有静态标定法和动态标定法。静态标定法是通过安装图纸对各叶片到达传感器的到达时间进行确定，该方法在实际使用中很难保证准确性与可操作性。原因在于两点，其一键相传感器的安装位置很容易发生改变；其二由于叶顶反射面的不确定性，很难确定感应信号的起跳边沿与叶片边沿对应。针对本实验台采用动态标定法标定理论到达时间。具体操作为，当传感器安装位置确定后，将磁铁激励去除，无激励情况下叶片的振动位移较小，通过对监测到的各叶片到达叶顶传感器与键相参考之间的时间差取平均值(注意应尽可能的保证转速稳定)，进而可以获得各叶片与不同叶顶传感器之间的理论到达时间值。

标定过程中发现，不同运转转速标定的理论到达时间有较小差别。为了减小转速变化带来的影响，采用阶梯转速的方式来标定理论到达时间，形成运转转速区间内的理论到达时间，有助于提高叶片振动位移测量的准确性。

3.1扫频测量过程

在扫频测量中，实验台均布安装6个磁铁激励，运转转频范围为60～132 Hz，通过四个叶顶传感器监测的叶片振动位移随转频的变化情况如图5所示。注意不同传感器对应的叶片编号一定要修正为物理下的同一叶片。

由图5可知叶片在该段运转区间内被激起较大振幅的谐共振区间有4个，如图中圆圈标记。分别对各谐共振区间段截取拟合，下面将着重介绍叶顶传感器1的拟合情况。

如对四个谐共振区截取范围分别为61～65 Hz，73～78 Hz，92～97 Hz，124～129 Hz。各谐共振区通过LM法拟合获得的振动位移曲线与原始数据之间的对比如图6所示。

通过LM法拟合获得的曲线参数见表1，另外三支传感器的振动位移响应曲线拟合过程相同，在此不做重复赘述。表2为四支传感器拟合参数的平均值，该参数值可反映叶片在各谐共振区内的谐共振中心频率，振动幅值以及振动恒偏量等。

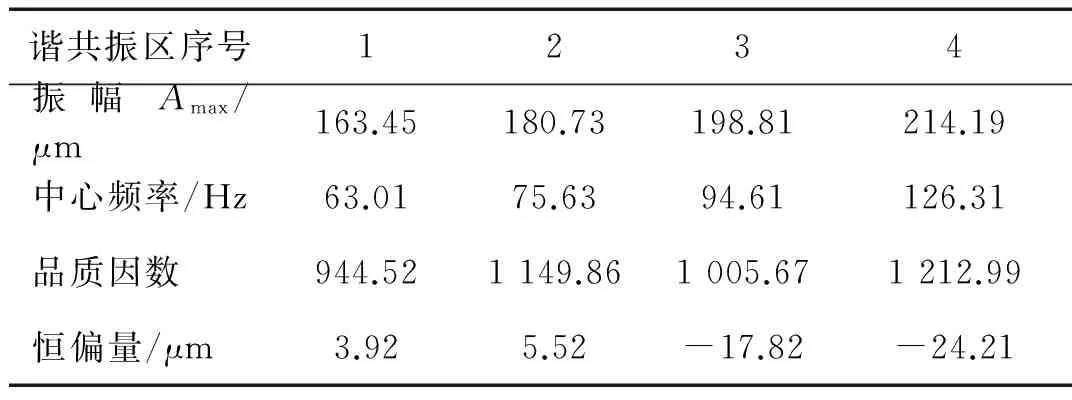
表1 相同叶顶传感器下各段拟合参数结果

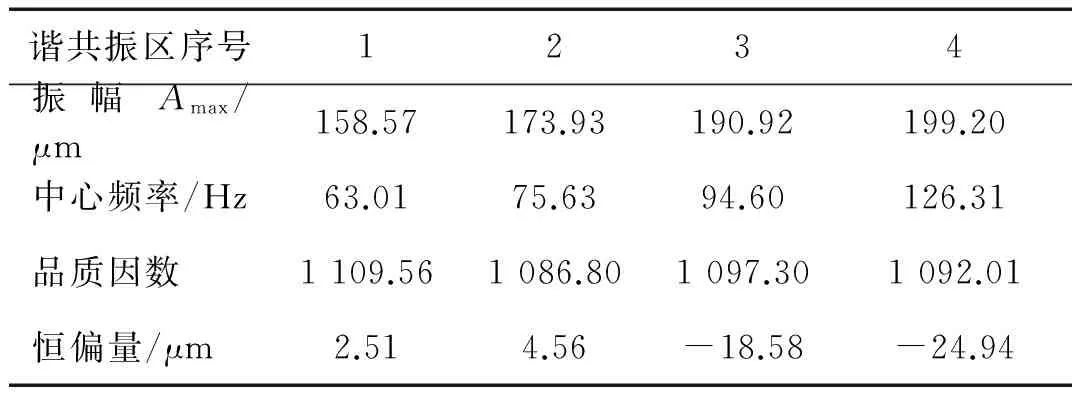
表2 四支传感器叶片在各谐共振区间拟合参数的平均值

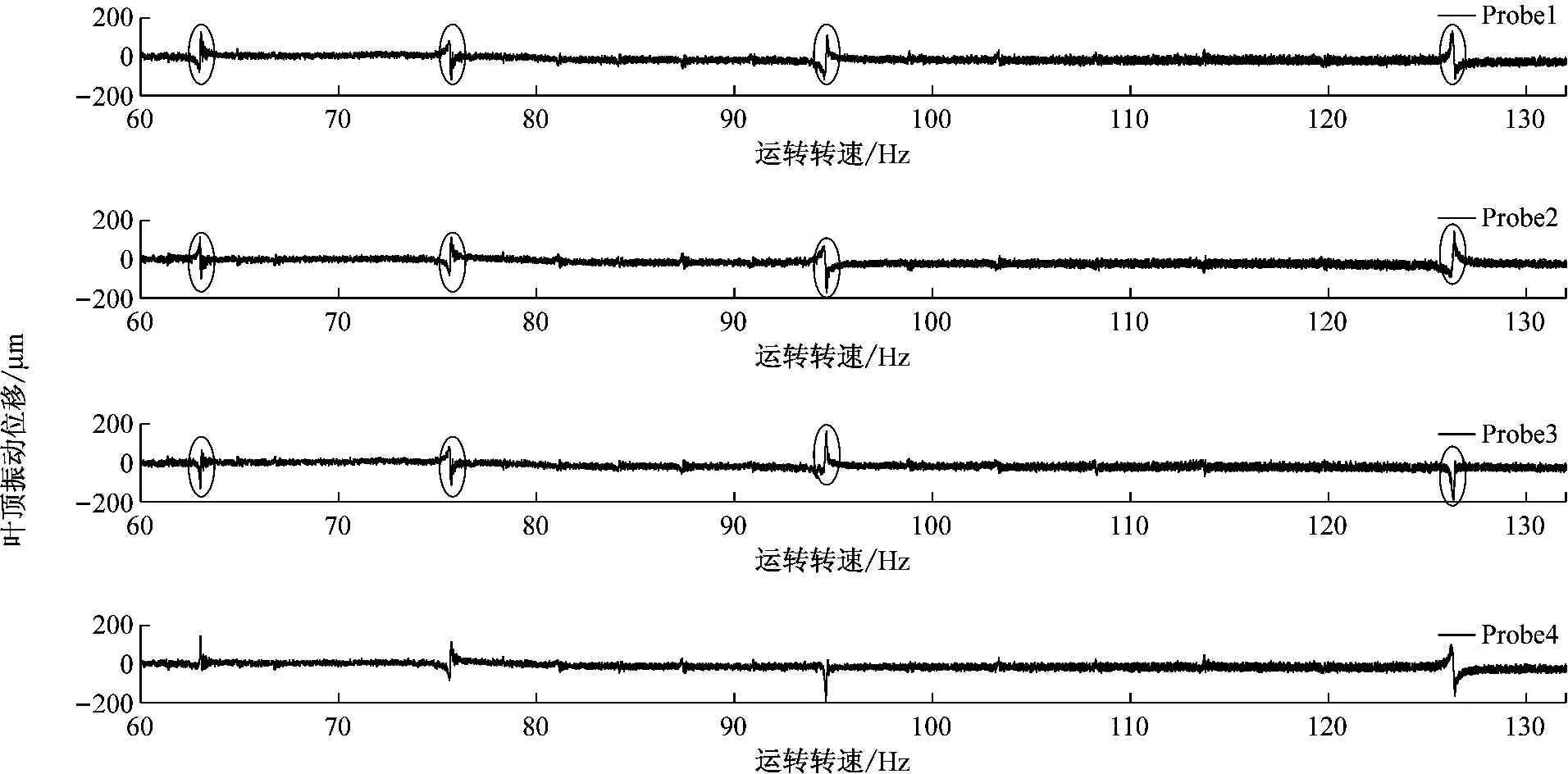
图5 四支传感器监测到的某一叶片振动位移响应情况

Fig.5 Blade vibration displacement response with four probe

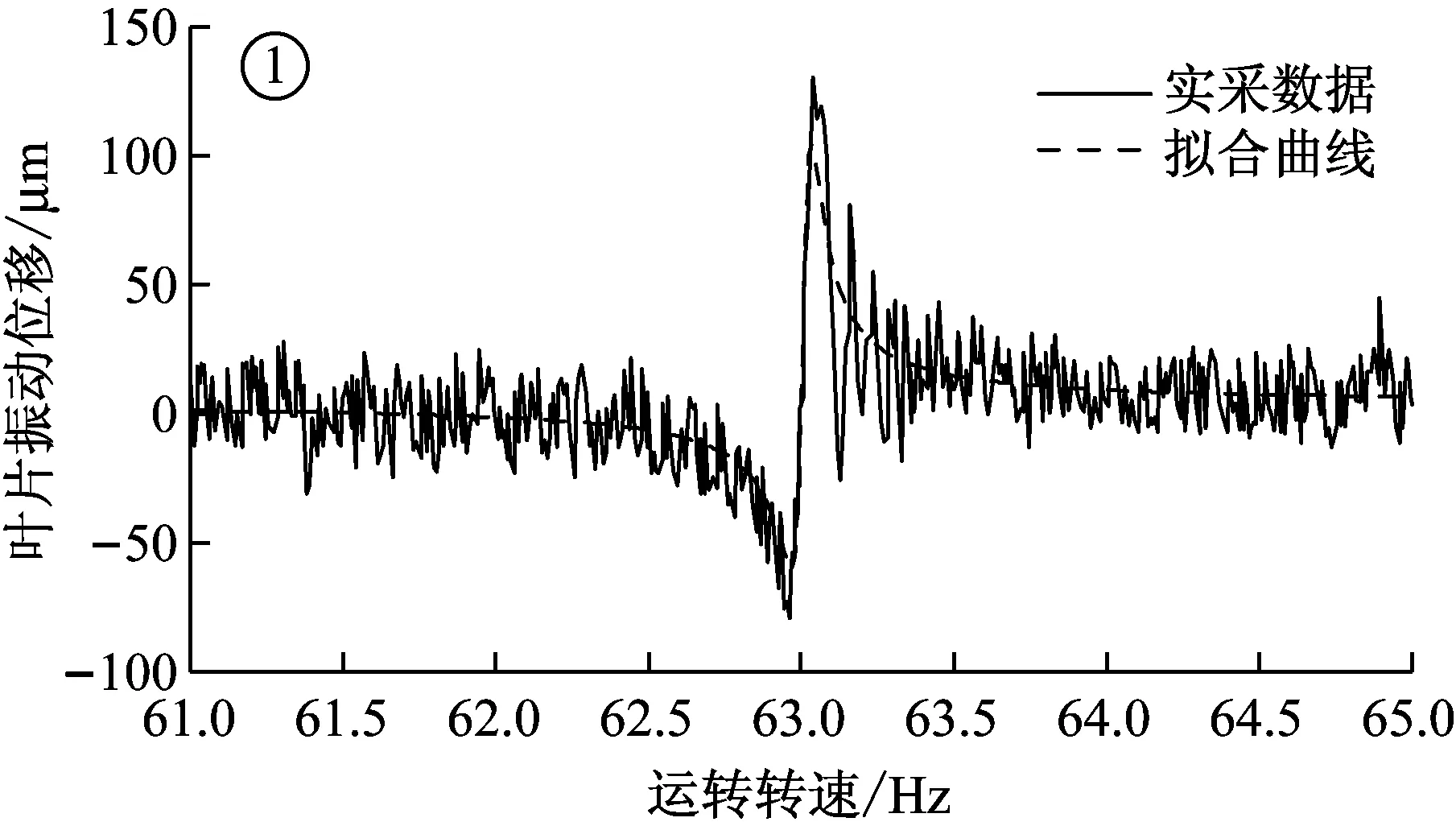
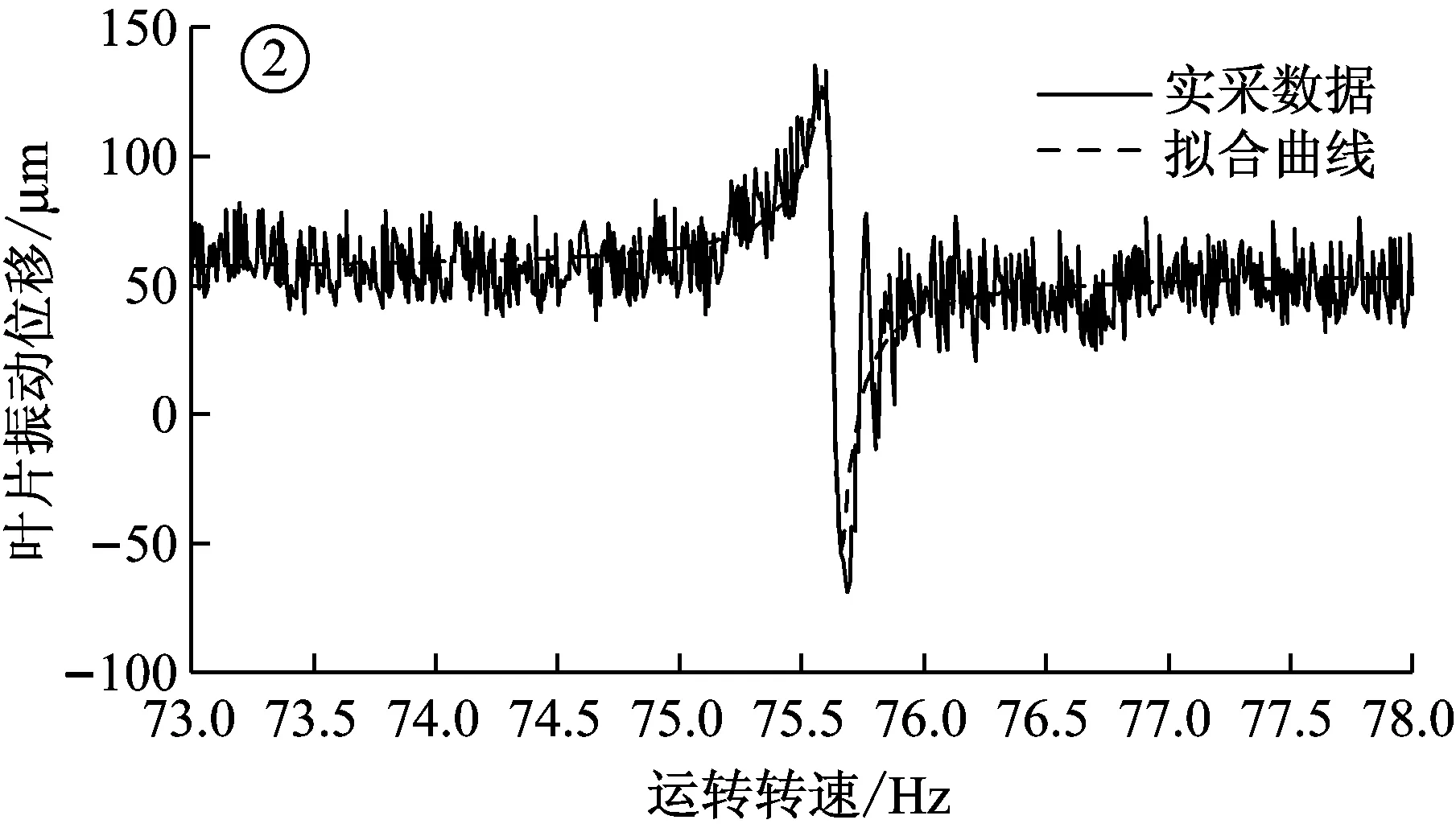
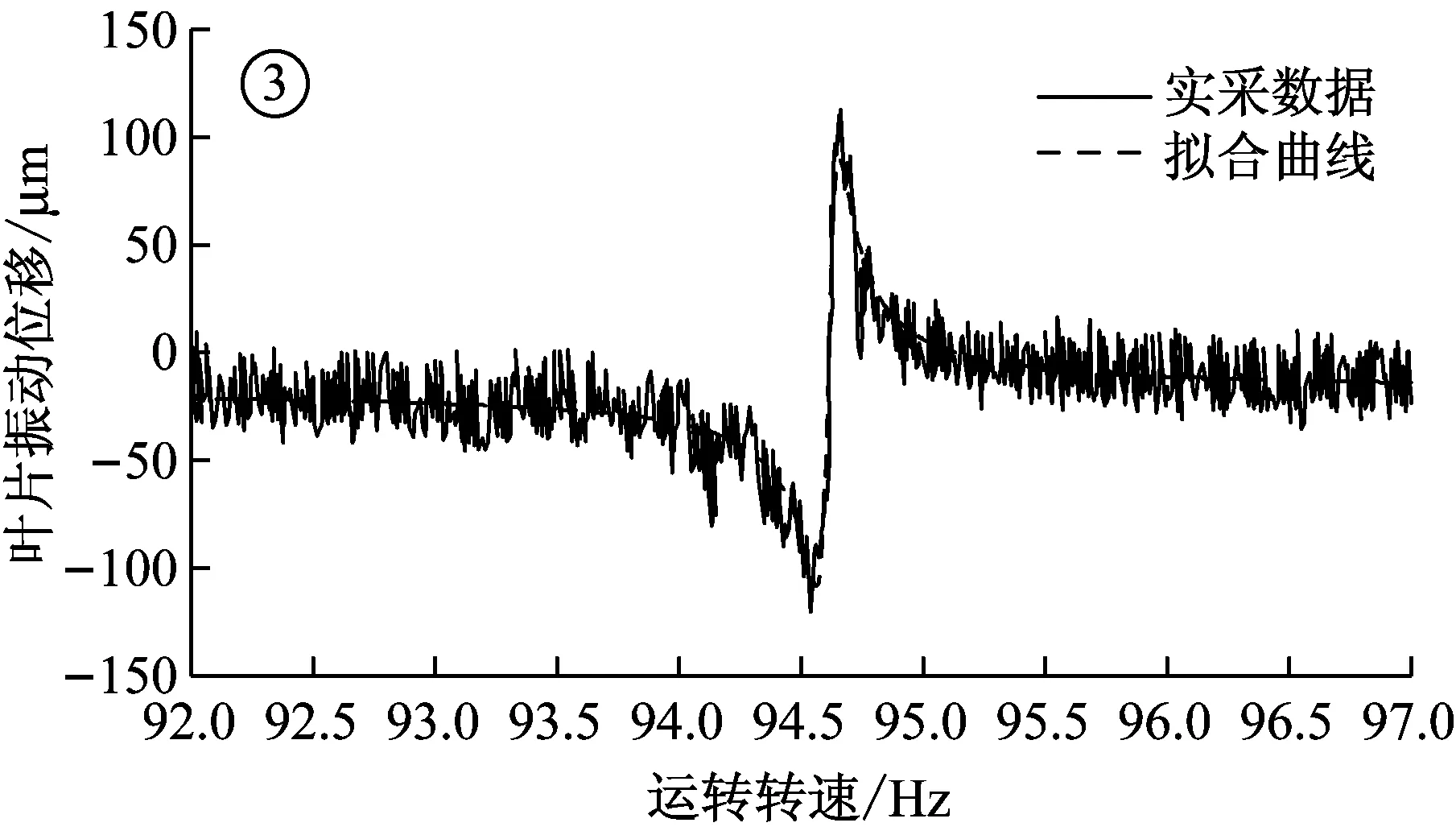
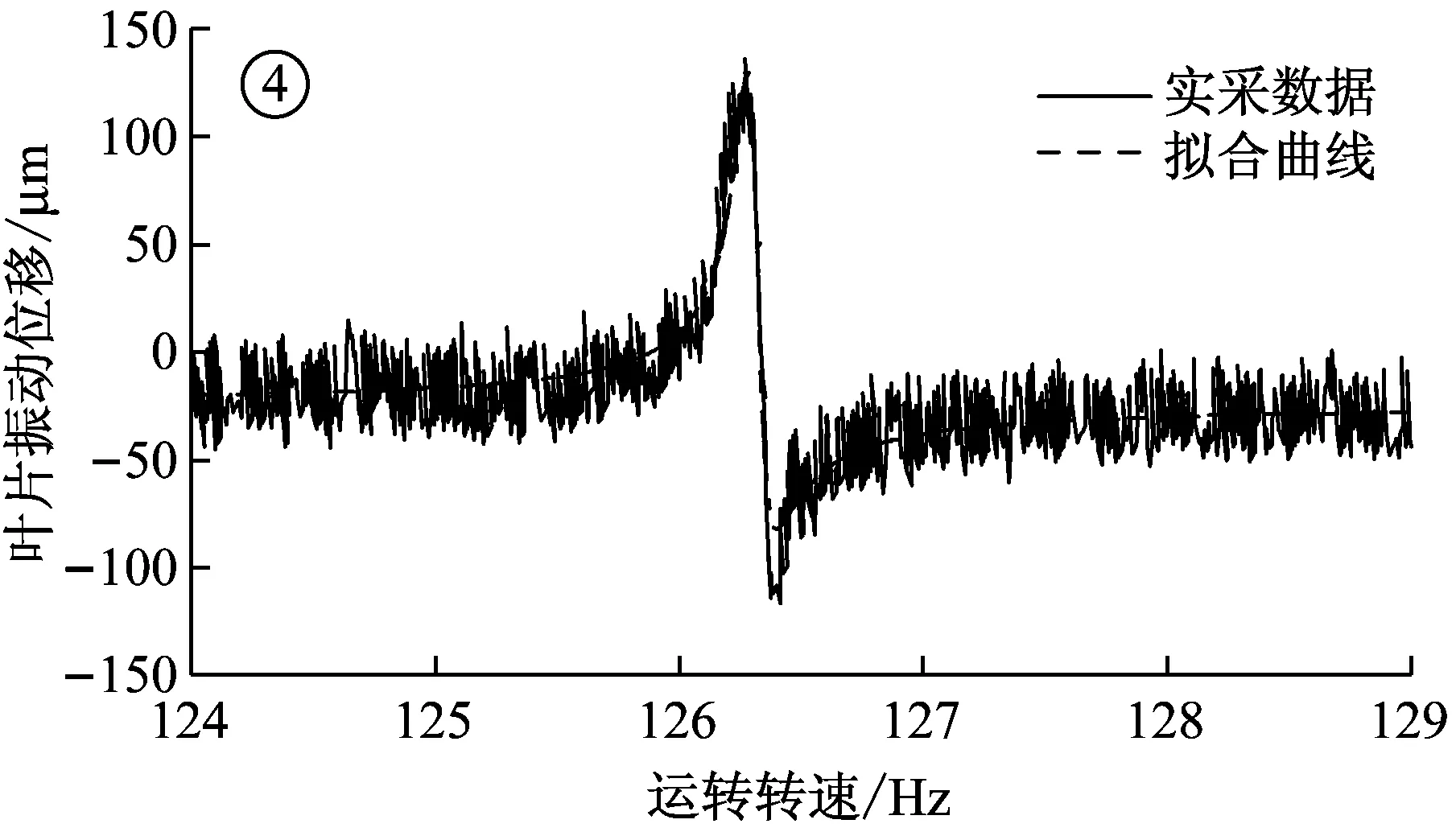
图6 各段原始曲线与拟合曲线之间的对比图

通过表1,2中获得谐共振中心频率，可以用作恒速运转求取对应振动倍频值时设定运转转速的参考值。

3.2恒速运转求取叶片振动倍频值

为了避免转速波动带来的影响，以及运行转速下叶片被激起的振动位移大小合适，实验中将恒速运转转速设定在谐共振中心频率附近，不用严格保证与中心频率一致。

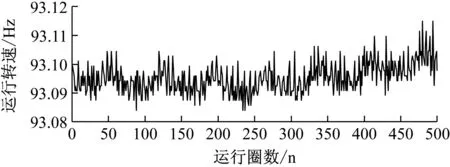
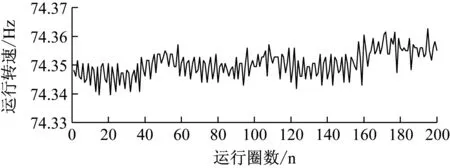
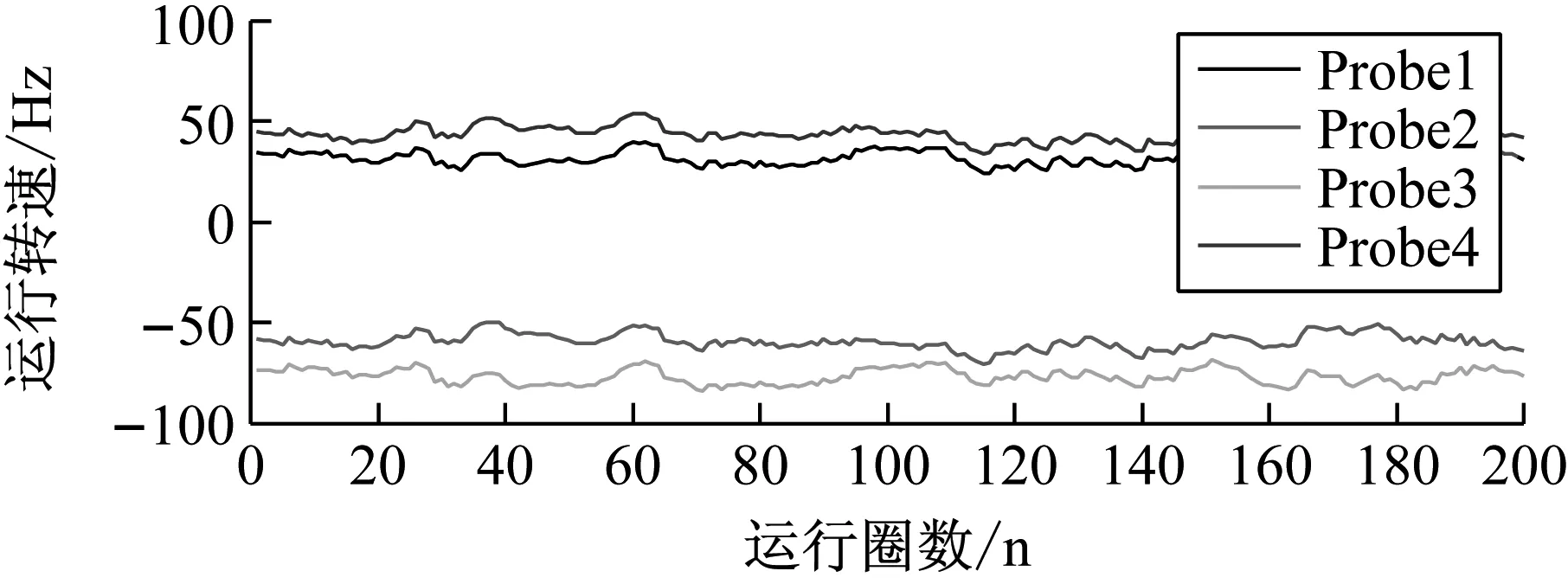
下面对上述存在的四个谐共振区分别恒速运转测量，图7为运转转频分别为124.44 Hz、93.1 Hz、74.35 Hz、61.96 Hz时叶片振动位移监测情况。图中对振动位移数据进行了7阶线性平滑处理。

上述四个恒速运转测量通过GARIV方法获得的叶片振动倍频值分别为18.07，24.45，30，25.38，取整后可得18，24，30，25。表3为各谐共振对应的叶片振动倍频值和动频值。

通过分析可知同一叶片对应的动频值应该是相同的，但谐共振中心频率为63.01 Hz对应的叶片振动频率值明显小于其他结果值。假设其余三个求得的叶片振动频率值是正确的，反求63.01 Hz对应的倍频值应该为36。该值比前期理论建模时假设的最大倍频值30大，要想通过GARIV方法获得准确的振动倍频值，则叶顶传感器的夹角应小于6°。通过本实验台的安装夹角是无法准确求出63.01 Hz对应的倍频值。

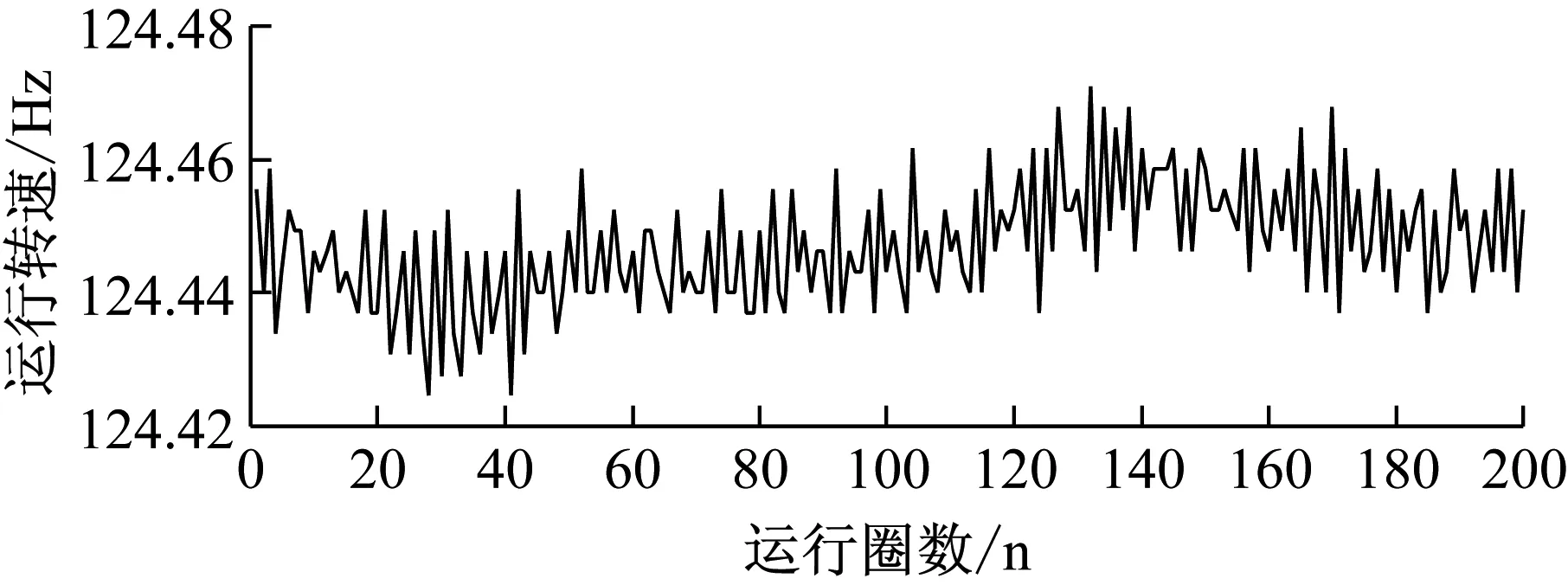
(a) 中心频率为126.31 Hz时的振动位移监测情况

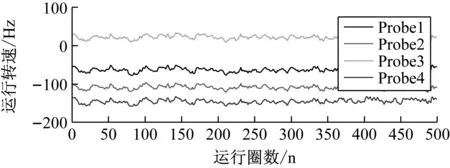
(b) 中心频率为94.6 Hz时的振动位移监测情况

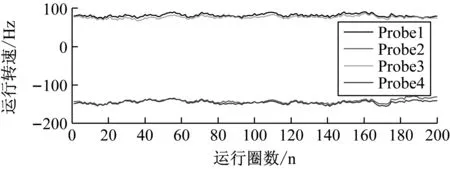
(c) 中心频率为75.63 Hz时的振动位移监测情况

(d) 中心频率为63.01 Hz时的振动位移监测情况

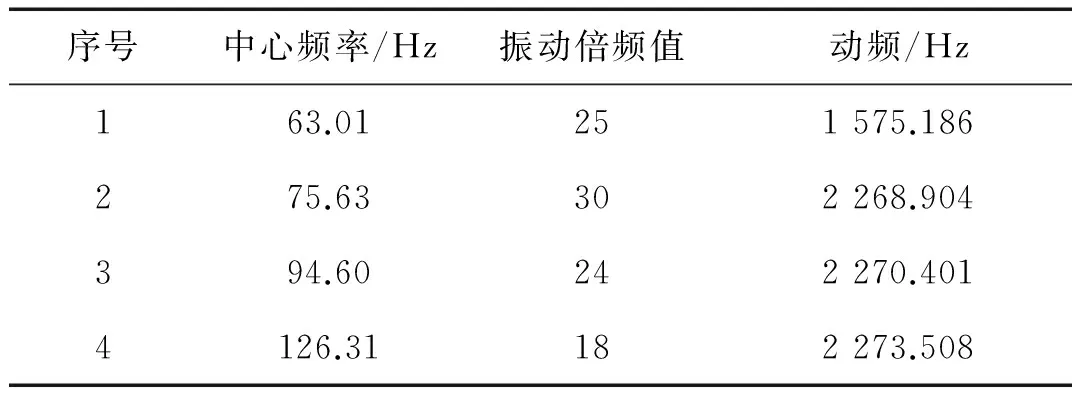
序号中心频率/Hz振动倍频值动频/Hz163.01251575.186275.63302268.904394.60242270.4014126.31182273.508

下面通过仿真模型进行验证，在仿真模型中假设存在倍频值为36的谐共振，叶顶传感器夹角设为6°。倍频值为36的谐共振通过GARIV方法分析得到的倍频值为25.04。进而验证了之前的推理，修正谐共振中心频率为63.01 Hz对应的振动倍频值为36。

3.3综合叶片振动参数及获得叶片振动坎贝尔图

通过扫频拟合和恒速运转测量可以辨识出叶片存在的谐共振区对应的同步振动参数，表4为六激励下叶片同步振动参数整理。

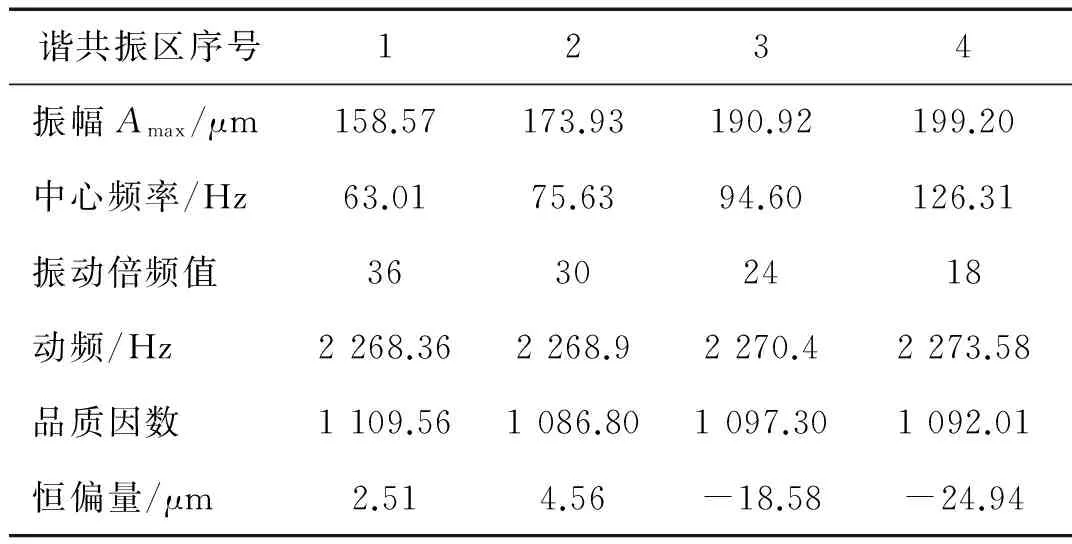
表4 叶片同步振动参数辨识结果

通过获得的叶片振动参数可以做出叶片振动坎贝尔图。图8为上述叶片对应的振动坎贝尔图。

3.4不同激励个数下的叶片振动分析

下面通过改变激励个数来研究叶片的谐共振情况，同时也可以对前文中测量结果进行验证。图9为叶顶传感器1监测的激励个数为12、4和3三种情况下的叶片振动位移随转速变化图。通过对存在的谐共振区进行拟合分析可以获得叶片的振动参数。结合前文获得的叶片振动频率值，可分别对存在的谐共振进行倍频值反推，进而分析倍频值是否与激励个数成倍数关系。三种激励个数下的叶片同步振动参数统计如表5所示。

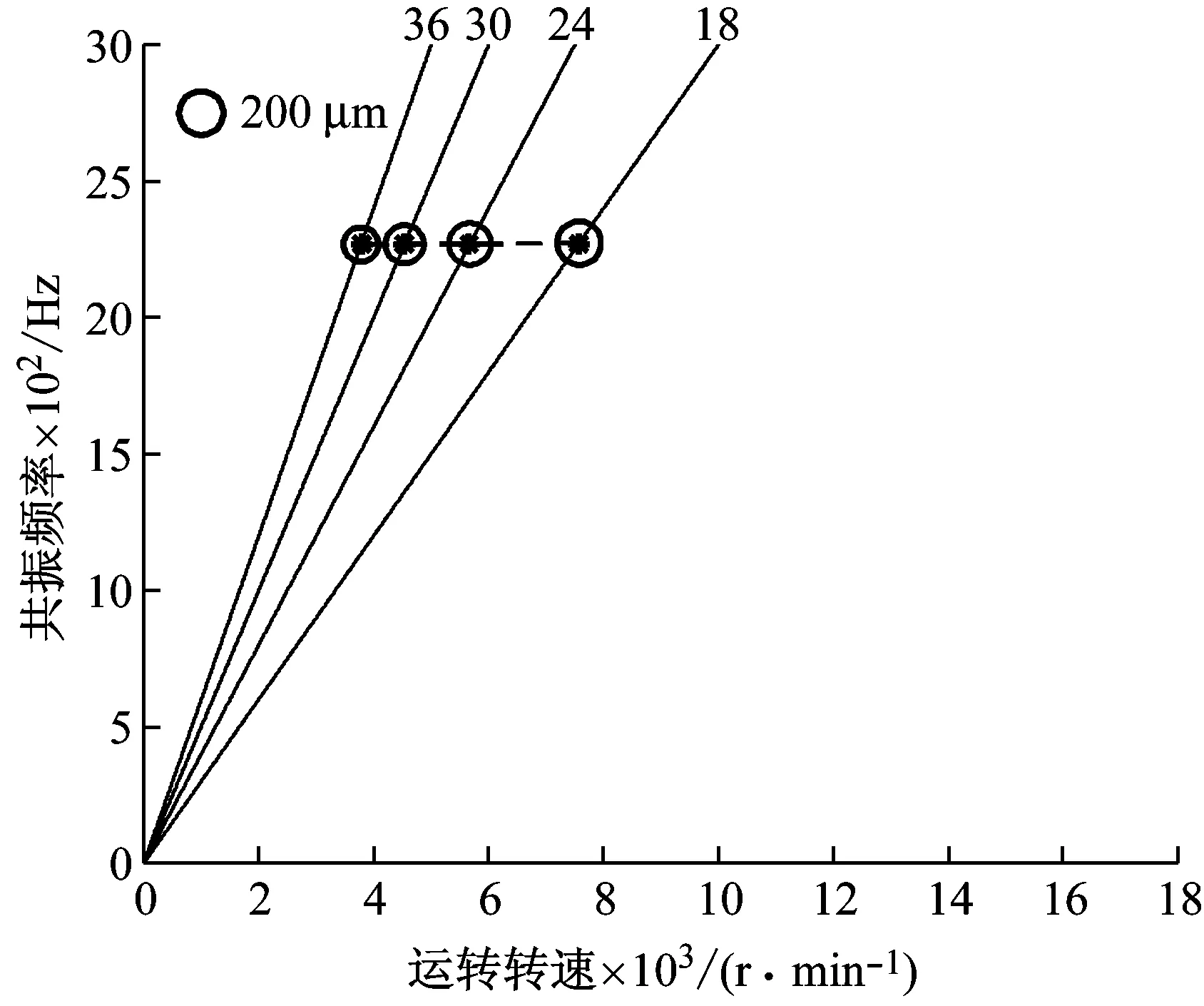
图8 六激励时某一编号叶片振动坎贝尔图

Fig.8 A certain number of blade vibration Campbell diagram when the number of incentives is six

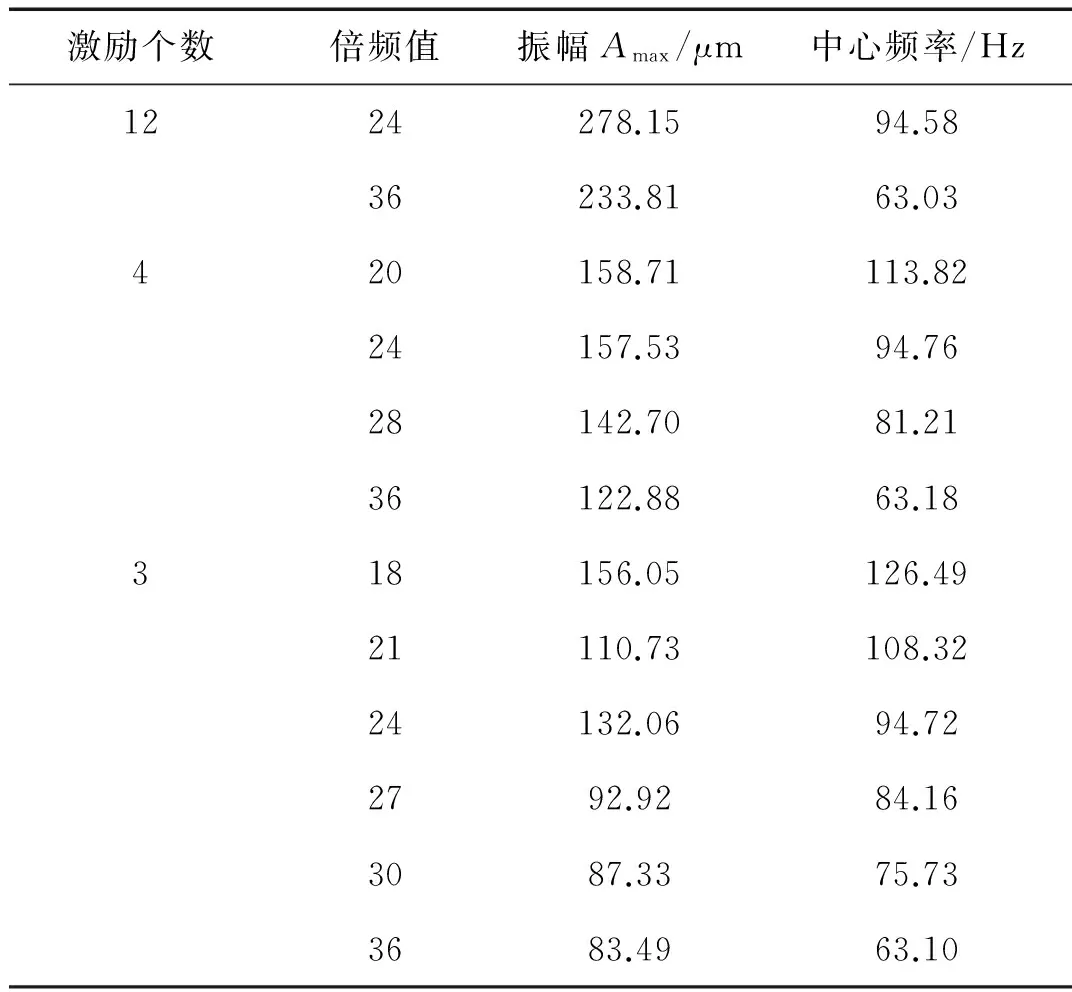
表5 不同激励个数下叶片同步振动参数

图9 相同传感器监测到的不同激励个数时叶片振动位移情况

通过表5分析可知，激励个数一定时，叶片被激起的谐共振对应的倍频值与激励个数之间成倍数关系；相同激励个数下，随着倍频值的增大，谐共振对应的振动幅值逐渐减小；当每个激励源提供相同激振力时，激励个数越多，被激起的叶片振动幅值越大。

4 结 论

本文基于变速扫频拟合和恒速运转下的GARIV法综合分析，将叶顶传感器使用数量减少到4个的基础上，较好的完成叶片同步振动参数辨识，获得了6激励个数时叶片振动的部分坎贝尔图。测量得到的一阶模态的振动频率为2 270 Hz，同理论计算值的2 140 Hz的偏差小于6%。整体上完成与理论研究相对应的方法验证。最后完成了不同激励个数下的叶片谐共振响应分析。由于叶片的振动幅值没有计算理论值，无法对比精度。

在后续的研究中，可继续增大转速，研究叶片高阶模态的响应。同时应该增加应变监测技术，从而开展非接触式应力测量技术的研究。另外还需开发小直径的光纤传感器，从而确保传感器之间的夹角更小，有利于获得更小夹角的传感器布置方案。但也由于传感器安装夹角的选取不够严谨导致该试验情况下振动倍频为36的情况没有被准确的识别出来。

[1] 王萍. 叶尖定时方法在国外航空发动机叶片振动测量中的应用综述[J]. 航空科学技术, 2013 (6): 5-9.

WANG Ping. Application review of blade tip timing method for foreign aero-engine blade vibration measurement[J]. Aeronautical Science & Technology, 2013(6):5-9.

[2] RUSSHARD P. Development of a blade tip timing based engine health monitoring system[D]. Manchester: Manchester University, 2010.

[3] CARRINGTON I B. Development of blade tip timing data analysis techniques[D]. Manchester: University of Manchester, 2002.

[4] 欧阳涛. 基于叶尖定时的旋转叶片振动检测及参数辨识技术[D]. 天津: 天津大学, 2011.

[5] 张玉贵, 段发阶, 方志强, 等. 间断相位法测量叶片同步振动幅值的研究[J]. 振动与冲击, 2008, 27(10): 183-186.

ZHANG Yugui, DUAN Fajie, FANG Zhiqiang, et al. Measuring synchronous vibration of rotating blades using discontinuous phase method[J]. Journal of Vibration and Shock, 2008, 27(10): 183-186.

[6] 欧阳涛, 郭文力, 段发阶, 等. 基于叶尖定时的旋转叶片同步振动辨识新方法[J]. 振动与冲击, 2011, 30(8): 249-252.

OUYANG Tao, GUO Wenli, DUAN Fajie, et al. New method for identifying rotating blades synchronous vibration based on tip-timing[J]. Journal of Vibration and Shock, 2011, 30(8): 249-252.

[7] CARRINGTON I B. Development of blade tip timing data analysis techniques[D]. Manchester: University of Manchester, 2002.

[8] DIMITRIADIS G, CARRINGTON I B, WRIGHT J R, et al. Blade-tip timing measurement of synchronous vibration of rotating bladed assemblies[J]. Mechanical Systems and Signal Processing, 2002,16(4): 599-622.

[9] PICKERING T M. Methods for validation of a turbomachinery rotor blade tip timing system[D]. Blacksburg Virginia Tech University, 2014.

[10] MANSISIDOR M R. Resonant blade response in turbine rotor spin tests using a laser-light probe non-intrusive measurement system[R]. Naval Postgraduate School Monterey ca, 2002.

[11] FREUND O, BARTELT M, MITTELBACH M, et al. Impact of the flow on an acoustic excitation system for aeroelastic studies[J]. Journal of Turbomachinery, 2013, 135(3): 583-595.

[12] FREUND O, MONTGOMERY M, MITTELBACH M, et al. Non-contact test set-up for aeroelasticity in a rotating turbomachine combining a novel acoustic excitation system with tip-timing[J]. Measurement Science and Technology, 2014, 25(3): 116-121.

Testsforsynchronousvibrationparametricidentificationmethodofaturbine’sblades

WANG Weimin, REN Sanqun, CHEN Lifang, SHAO Huajin

(Beijing Key Laboratory of Health Monitoring Control and Fault Self-recovery for High-end Machinery, Beijing University of Chemical Technology, Beijing 100029, China)

Accurate measurement of blade vibration using as few as possible sensors and more compact installation space is indispensable for engineering applications. Based on the measurement technique of BTT, the combination of the rotating speed-varying sweep frequency fitting method and GARIV one was proposed and tested to identify a turbine’s blades synchronous vibration parameters here. A high-speed straight blade test rig was established (the maximum rotating speed is 45 000 r/min, and the blade tip velocity is 322.8 m/s). In tests, the parametric identification of blade synchronous vibration was conducted and Campbell diagram of blade vibration was correctly plotted under the excitation of six magnets. Furthermore, tests and analyses of blade harmonic vibration under different numbers of excitation were done. Through comparison, it was shown that the maximum error between the calculation results of blade’s dynamic stress modes and the corresponding test ones is less than 6%. This method provided a technical way for blade fault early warming and dynamic stress non-contact measurement.

BTT; GARIV; synchronous vibration; parametric identification

国家自然科学基金(51275028; 51135001)

2016-11-01 修改稿收到日期：2016-12-16

王维民 男，博士，教授，1978年4月生

陈立芳 女，博士，讲师，1973年3月生

TK14； V216.2

： A

10.13465/j.cnki.jvs.2017.17.020