间隙铰链对平面机构碰撞动力学特性影响分析

王旭鹏, 刘 更, 马尚君, 佟瑞庭, 薛艳敏

(1. 西安理工大学 艺术与设计学院工业设计系， 西安 710054；2. 西北工业大学 陕西省机电传动与控制工程实验室，西安 710072)

间隙铰链对平面机构碰撞动力学特性影响分析

王旭鹏1, 刘 更2, 马尚君2, 佟瑞庭2, 薛艳敏1

(1. 西安理工大学 艺术与设计学院工业设计系， 西安 710054；2. 西北工业大学 陕西省机电传动与控制工程实验室，西安 710072)

为了研究间隙铰链对机构动态性能的影响，建立了一种含轴向尺寸的线接触碰撞铰模型，在此基础上提出一种改进的非线性法向碰撞力模型和修正的切向库伦摩擦力模型，以平面含间隙铰链曲柄滑块机构为研究对象，通过不同间隙值下的滑块加速度、间隙铰链处接触力、加速度频谱以及速度-加速度相图分析，研究了间隙值对机构碰撞动力学特性的影响规律。研究结果表明：间隙会导致机构动态性能出现明显的振荡现象，且随着间隙值的增大，振荡加剧、振荡幅值上升，但振荡频率降低；同时，在间隙铰链的影响下，机构动态特性呈现出非线性现象,且间隙越大，非线性现象越明显。

非线性碰撞力模型；间隙铰链；碰撞动力学

机构运动中相邻构件间铰链连接处通常设计有合理的间隙。同时，加工和装配带来的误差，以及使用过程中摩擦磨损的影响，会使间隙值进一步扩大[1-2]。间隙铰链处产生的接触力会引起机构动态特性产生明显的振荡，进而导致机构运动精度和可靠性降低，即便很小的间隙值，也会导致机构动态特性产生高频振荡[3]。

从20世纪70开始，间隙铰链对机构动态特性的影响逐渐成为了国内外研究的热点。Dubowsky等[4]研究者基于Kelvin-Voigt[5]线性弹簧阻尼模型进行了一系列含间隙机构动态特性方面的理论和实验研究[6-10]；Lankarani等[11]在Hunt等[12]研究工作的基础上，提出了一种目前应用最广泛的、基于Hertz接触理论和恢复系数的非线性弹簧阻尼模型。Paulo Flores等[13-14]研究者基于Lankarani-Nikravesh模型开展了间隙值、间隙数量、驱动载荷以及油膜润滑对含间隙机构动态特性影响方面的研究；闫绍泽等[15-17]开展了含间隙铰航天器动力学建模、数值模拟以及非线性等一系列问题研究，通过数值仿真分析，对含间隙空间可展开机构非线性问题进行了研究；黄铁球等[18]针对含间隙铰链大型桁架式伸展机构进行了仿真分析，得到了结构的非线性动响应情况，并与实验数据进行了对比分析，验证了仿真的有效性。陈鹿民等[19]通过实验研究了微重力环境下含间隙转动副航天可展开结构的动力学特性，发现航天器水平吊装比垂直安装对间隙铰链运动状态敏感性更高。基于ADAMS软件，郝雪清等[20]研究了间隙铰链处的材料对含间隙机构动力学特性的影响；白争锋等[21]在研究改进弹性基础模型基础上提出了一种改进的非线性法向碰撞力混合模型和改进的库伦摩擦力模型，并基于该模型进行了相关分析研究[22]；Liu等[23]基于弹性基础模型，提出了一种改进的接触计算模型，通过与有限元计算结果进行对比分析，发现模型具有更好的适应性；王旭鹏等基于文献[23-24]提出了一种考虑铰链轴向尺寸，且计算过程不需要恢复系数的、近似的法向碰撞力模型，并结合数值仿真以及实验数据对比验证了模型的有效性[25]；之后，进一步对文献[25]中的模型进行改进，相继提出了另外两种法向碰撞力模型，并通过不同间隙、初始碰撞速度及不同恢复系数下的对比分析，发现改进模型在不同工况下均比L-N模型具有更高的精度[26]。

本文基于改进的非线性法向碰撞力模型和修正的切向库伦摩擦力模型，以含间隙铰链曲柄滑块机构为研究对象，通过不同间隙下的数值仿真分析，研究了间隙值对含间隙铰链机构接触特性和碰撞动力学特性的影响规律。

1 间隙铰链建模

建立准确的间隙铰链模型，是进行含间隙机构碰撞动力学分析的基础所在。本文采用碰撞铰模型，并考虑了轴承轴向尺寸，建立了如图1所示的线接触间隙铰链模型，其径向间隙值可表示为：

ΔR=rB-RJ

(1)

式中，rB、rJ分别为轴和轴承的半径。

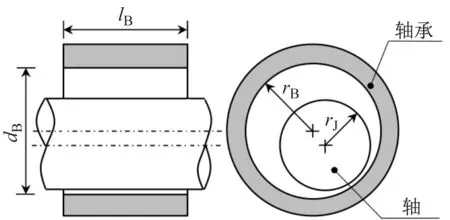
图1 含轴承轴向尺寸的间隙铰链模型

由图2所示广义坐标系XOY下的间隙铰链碰撞模型可知，轴承与轴中心点的偏心向量可以表示为

(2)

对应的偏心距离为

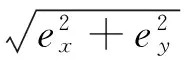
(3)

发生碰撞时，轴与轴承间的弹性变形量为

δ=e-ΔR

(4)

当δ≥0时表示轴与轴承间发生接触和碰撞，此时对应

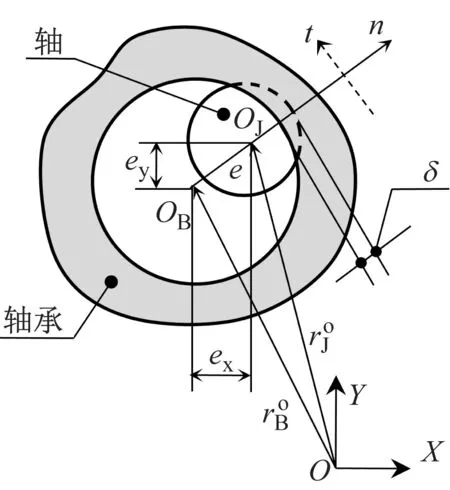
图2 广义坐标系XOY下的间隙铰链碰撞模型

碰撞点处的法向和切向速度分别为

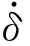
(5)

式中，n为单位法向量，且n·t=0。

2 间隙铰链处接触力模型

当间隙铰链处轴、轴承发生接触碰撞时，将产生由法向碰撞力和切向摩擦力组成的接触力；因此，建立准确的接触力模型，对于含间隙铰链机构碰撞动力学研究起到至关重要的作用。

2.1法向碰撞力模型

基于图1所示的线接触间隙铰链模型，文献[26]提出如下假设：① 轴和轴承间为正碰撞，即二者的轴线在同一平面内、且平行；② 沿接触线方向上任意点处的碰撞效果接近或相同；③ 忽略沿轴承轴向方向相邻两单元间的相互作用。从而建立了一种改进的非线性法向碰撞力模型，并通过不同间隙、不同初始碰撞速度以及不同恢复系数下轴、轴承间单次碰撞-恢复过程的仿真分析，以及与含间隙机构实验数据进行对比分析，发现改进的模型比目前应用最广泛的Lankarani-Nikravesh模型具有更高的计算精度，该模型表达式如下：

(6)

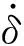
(7)

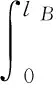
式中：L为轴承轴向长度；E*为轴、轴承材料的等效弹性模量，可由下式获得：

(8)

式中：E1,2和v1,2分别为轴、轴承材料的弹性模量和泊松比。

此外，公式(6)中Fi为任意接触点处的法向碰撞力，其表达式为

(9)

2.2切向摩擦力模型

在文献[19,24]的基础上，文献[25]提出了另外一种改进的切向摩擦力模型，如图3所示，其表达式为

FT=-μ(vT)FN

(10)

μ(vT)=

(11)

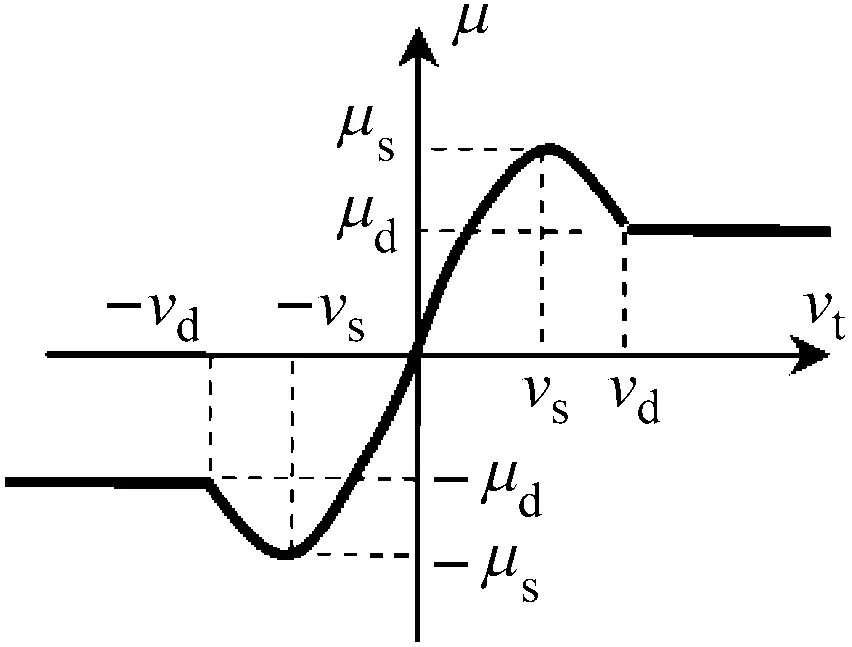
图3 修正的库伦摩擦力模型

3 碰撞动力学仿真分析

如图4所示，曲柄滑块机构连杆与滑块间铰链处存在规则径向间隙，其余各处均为理想约束。机构几何参数和质量特性参数如表2所示，仿真分析参数，如表2所示。

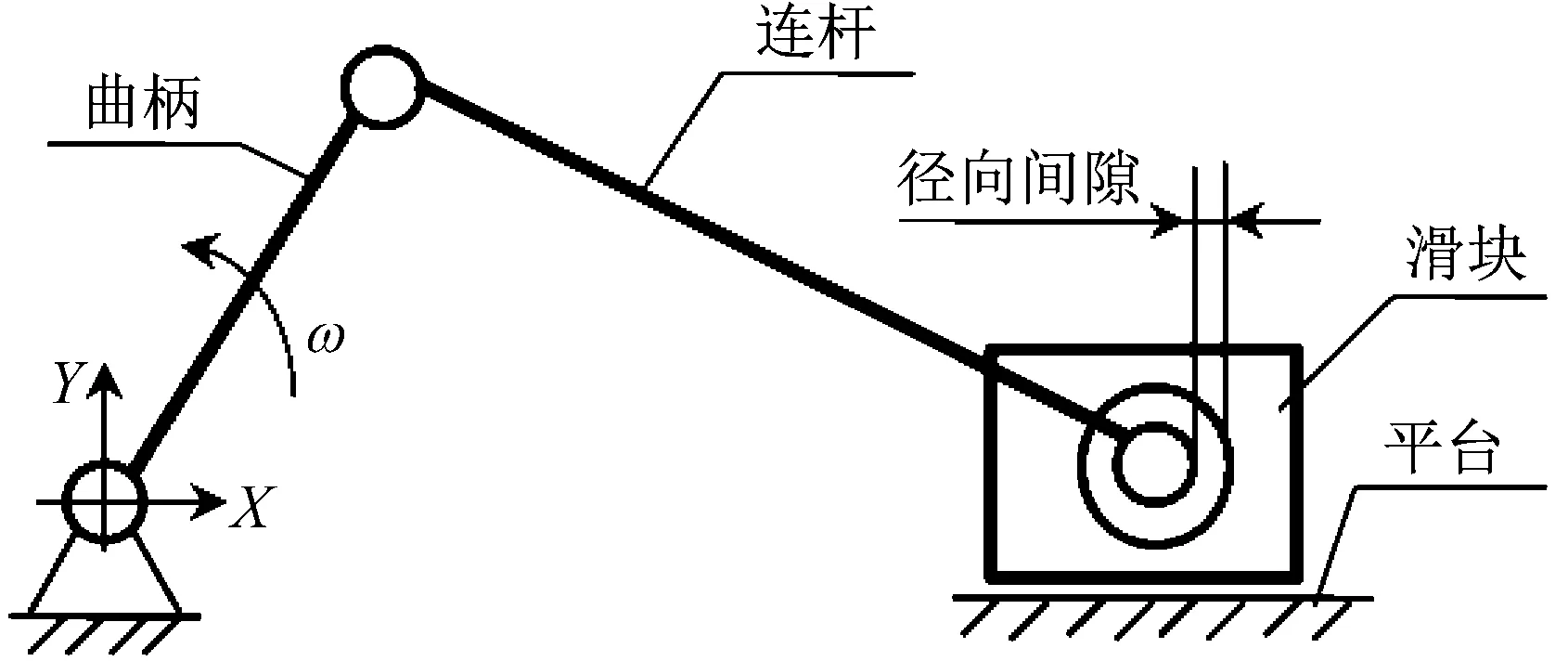
图4 含间隙铰链曲柄滑块机构模型

为了研究间隙值对机构碰撞动力学特性的影响，假设间隙铰链处径向间隙分别为0.1 mm、0.3 mm、0.5 mm及1 mm，且无润滑；仿真过程中曲柄转速恒定为500 r/min；同时不考虑杆件弹性变形影响，仿真结果如图5～图7所示。

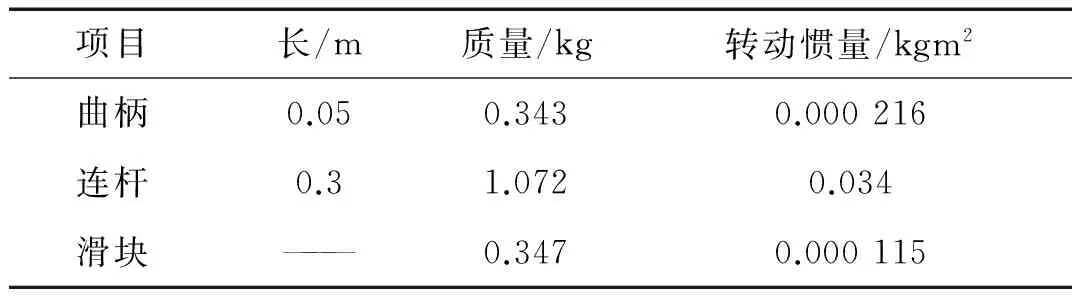
表1 机构几何参数和质量特性参数

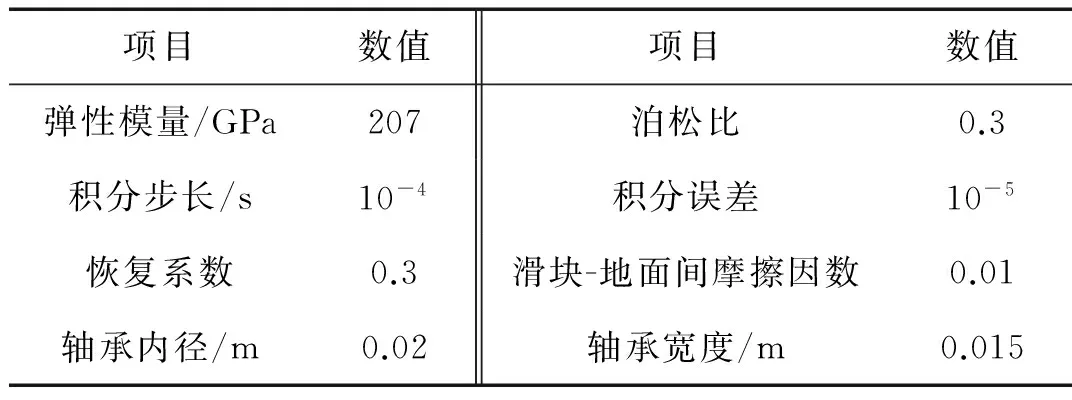
表2 动力学仿真参数

(b) 局部放大视图

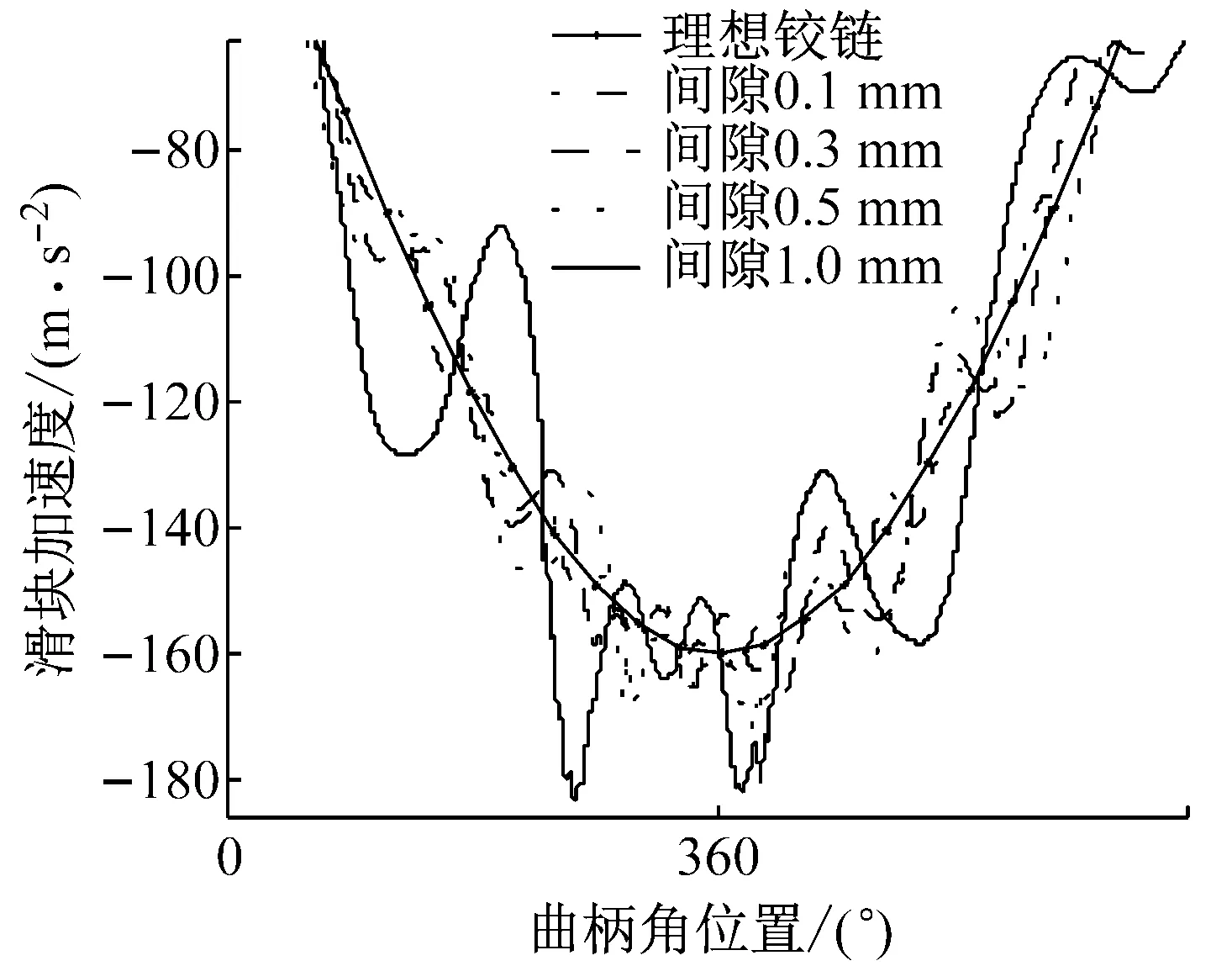
分析图5～图6可知：在间隙的影响下，滑块动态加速度和间隙铰链处接触力均出现了明显的振荡；随着间隙值的增大，机构动态输出曲线振荡加剧，相对于理想曲线的误差也进一步扩大，如不同间隙值下的加速度相对误差分别为3.76%、9.46%、17.08%以及37.92%；且最大振荡点均出现在180°、360°及540°附近，即机构的死点位置附近；这说明由于间隙的存在，导致在铰链处产生了明显的接触碰撞现象，且间隙越大，碰撞力越大。

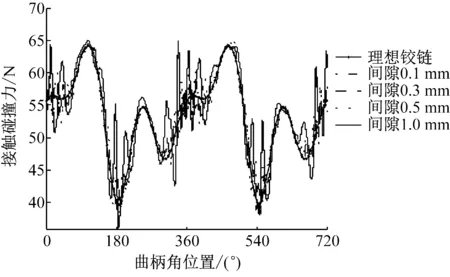
(a) 2个周期内仿真结果

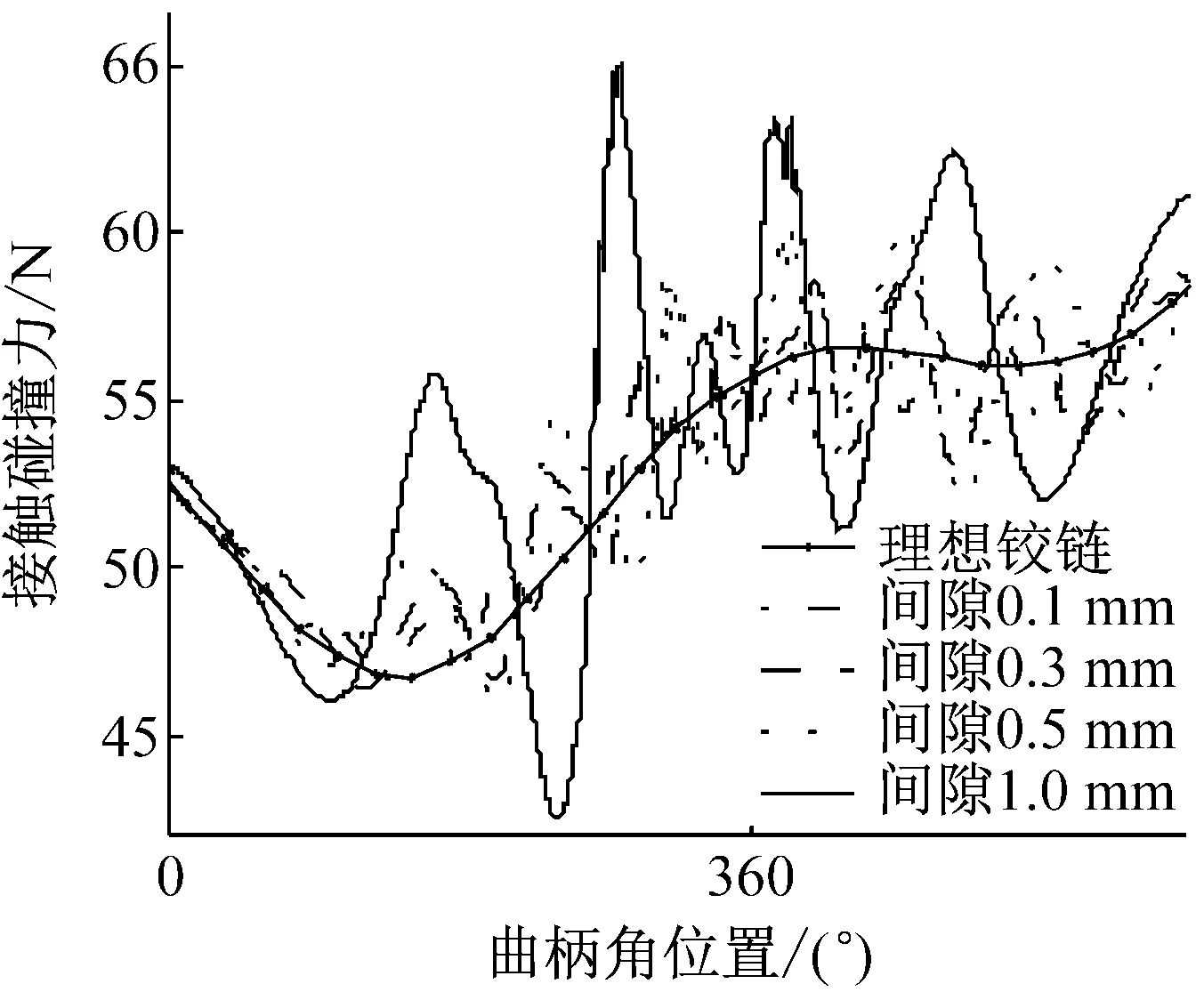
(b) 局部放大视图

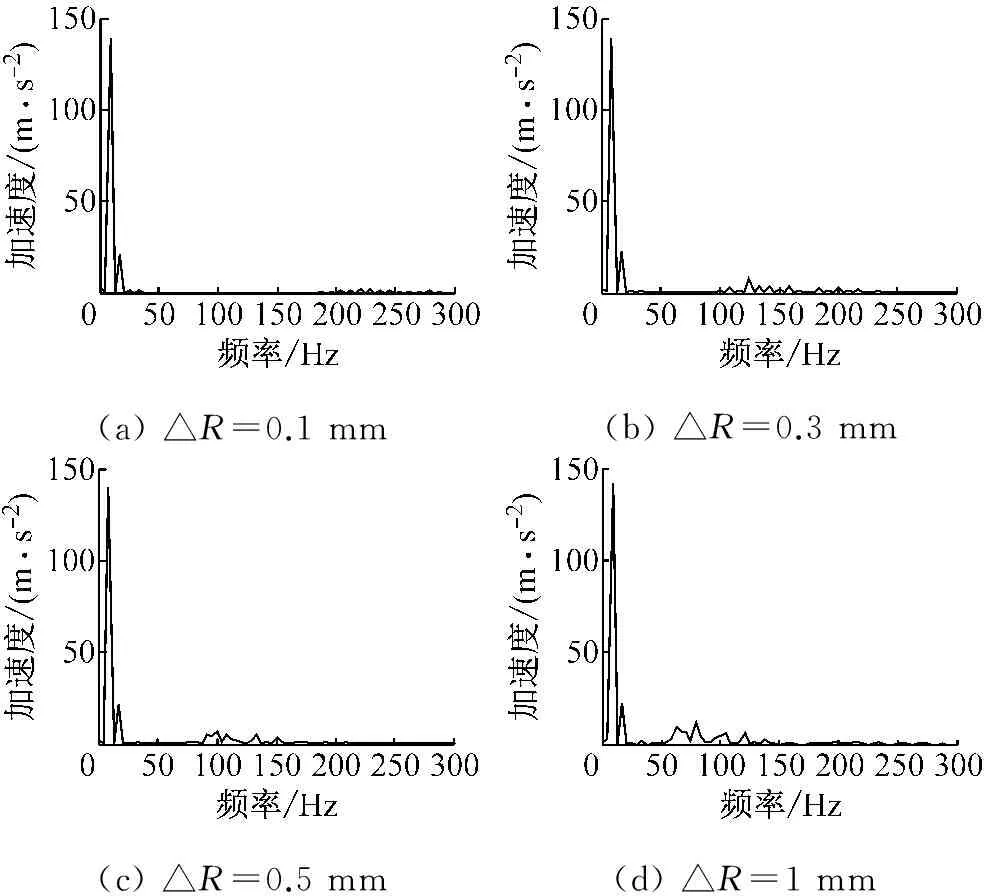
(a)△R=0.1mm(b)△R=0.3mm(c)△R=0.5mm(d)△R=1mm

图7 不同间隙下滑块加速度频谱图

Fig.7 FFT analysis of slider acceleration for different clearance sizes

图7所示为不同间隙值下滑块加速度频谱图，分析可知：当径向间隙由0.1 mm逐渐增加至1 mm时，加速度主频及幅值基本保持不变；同时，随着间隙值的增大，加速度高频范围逐渐降低，但高频幅值不断增大；不同间隙值下的高频范围分别为200～300 Hz、100～220 Hz、85～160 Hz和50～150 Hz，对应的最大幅值分别为2 m/s2、6.7 m/s2、7.2 m/s2和12.2 m/s2。可见在小间隙下，加速度振荡表现出高频、低幅值特点；但随着间隙的增大，出现低频、高幅值特点。这种现象说明，在小间隙下，轴和轴承间连续两次碰撞间的时间间隔很短，且碰撞力较小；当间隙值变大时，相邻两次碰撞间隔时间变长，碰撞力变大。

图8所示为不同间隙值下滑块速度-加速度相图，分析可知：在铰链处间隙的影响下，机构动态特性呈现出明显的非线性特性；且随着间隙值的逐渐增大，非线性现象变得越发明显。

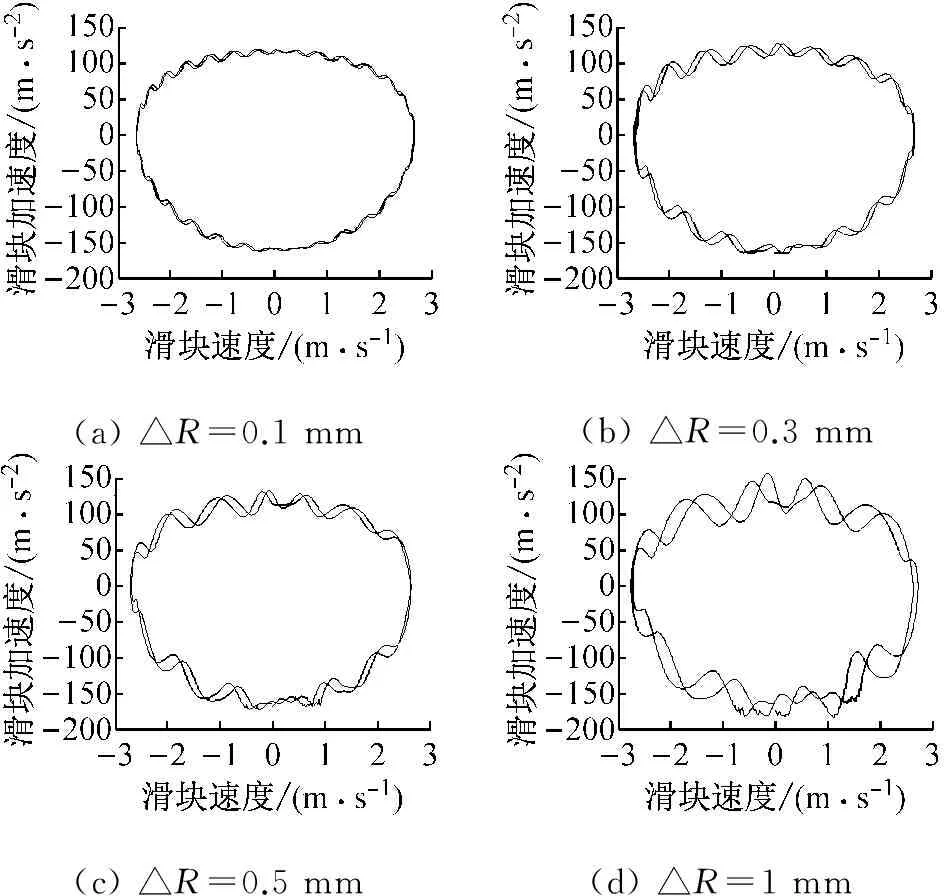
(a)△R=0.1mm(b)△R=0.3mm(c)△R=0.5mm(d)△R=1mm

图8 不同间隙下滑块速度-加速度相图

Fig.8 Phase diagram of velocity-acceleration for different clearance sizes

4 结 论

基于含间隙铰链处轴承轴向尺寸的线接触碰撞铰模型，和改进的非线性接触力模型，以平面含间隙铰链的曲柄滑块机构为例，进行了不同间隙值下的动力学仿真分析，研究表明：

(1) 铰链处间隙会导致机构动态输出在死点位置附近出现明显的振荡现象。

(2) 转速为500 r/min时，不同间隙值下振荡主频和幅值基本相同；而随着间隙值的增大，高频段频率逐渐降低，但振荡幅值逐渐增大；表明在大间隙下，每个周期内碰撞次数减少，但碰撞力变大。

(3) 在间隙的影响下，机构动态输出呈现出非线性特点，且间隙值越大，非线性特性越明显。

此外，本文研究中没有考虑间隙铰链处的润滑和杆件弹性变形的影响，应在后续研究中予以考虑。

[1] FLORES P, AMBRSIO J. Revolute joints with clearance in Multibody systems[J]. Computers and Structures, 2004, 82(17/18/19): 1359-1369.

[2] FLORES P. A parametric study on the dynamic response of planar Multibody systems with multiple clearance joints[J]. Nonlinear Dynamics, 2010, 61(4): 633-653.

[3] WANG Xupeng, LIU Geng. Modeling and simulation of revolute joint with clearance in planar multi-body systems[J]. Journal of Mechanical Science and Technology, 2015, 29(10): 4113-4120.

[4] DUBOWSKY S. On predicting the dynamic effects of clearances in planar mechanisms[J]. ASME Journal of Engineering for Industry, 1974, 96 (1): 317-323.

[5] GOLDSMITH W. Impact-the theory and physical behaviour of colliding solids[M]. London, England: Edward Arnold Ltd., 1960.

[6] DUBOWSKY S. On predicting the dynamic effects of clearances in one-dimensional closed loop systems[J]. ASME Journal of Engineering for industry,1974, 96B: 324-329.

[7] DUBOWSKY S, GARDNER T N. Design and analysis of multilink flexible mechanisms with multiple clearance connections[J]. ASME Journal of Engineering for industry, 1977, 99(1): 88-96.

[8] DUBOWSKY S, FREUDENSTEIN F. Dynamic analysis of mechanical systems with clearances, Part 1: formulation of dynamic model[J]. Journal of Engineering for Industry, 1971, 93: 305-309.

[9] DUBOWSKY S, FREUDENSTEIN F. Dynamic analysis of mechanical systems with clearances, Part 2: dynamic response[J]. Journal of Engineering for Industry, 1971, 93: 310-316.

[10] DUBOWSKY S, MOENING M F. An experimental and analytical study of impact forces in elastic mechanical systems with clearances[J]. Mechanism and Machine Theory, 1978, 13: 451-465.

[11] LANKARANI H M, NIKRAVESH P E. A contact force model with hysteresis damping for impact analysis of multi-body systems[J]. Journal of Mechanical Design, 1990, 112: 368-376.

[12] HUNT K H, CROSSLEY F R E. Coefficient of restitution interpreted as damping in vibroimpact[J]. Journal of Applied Mechanics, 1975, 7: 440-445.

[13] FLORES P. Modeling and simulation of wear in revolute clearance joints in multibody systems[J]. Mechanism and Machine Theory, 2009, 44: 1211-1222.

[14] FLORES P, KOSHY C S, LANKARANI H M, et al. Numerical and experimental investigation on Multibody systems with revolute clearance joints[J]. Nonlinear Dynamics, 2011, 65(4):383-398.

[15] 阎绍泽, 陈鹿民, 季林红, 等. 含间隙铰机械多体系统动力学模型[J]. 振动工程学报, 2003, 16(3): 290-294.

YAN Shaoze, CHEN Lumin, JI Linhong, et al. Dynamic modeling of multibody system with clearance joints[J]. Journal of Vibration Engineering, 2003, 16(3): 290-294.

[16] 阎绍泽, 申永胜, 陈洪彬. 考虑杆件柔性和铰间隙的可展结构动力学数值模拟[J]. 清华大学学报(自然科学版)，2003, 43(2): 145-148.

YAN Shaoze, SHEN Yongsheng, CHEN Hongbin. Dynamic performance of deployable structures with flexible members and clearance connections[J]. Journal of Tsinghua University(Science and Technology), 2003, 43(2): 145-148.

[17] 阎绍泽. 航天器中含间隙机构非线性动力学问题及其研究进展[J]. 动力学与控制学报, 2004, 2(2): 48-52.

YAN Shaoze. Development and problems of nonlinear dynamics of the mechanism with clearances for spacecraft[J]. Journal of Dynamics and Control, 2004, 2(2): 48-51.

[18] 黄铁球, 吴德隆, 闫绍泽, 等.带间隙伸展机构力学仿真研究[J].中国空间科学技术,1999, 3: 16-22.

HUANG Tieqiu, WU Delong, YAN Shaoze, et al. Dynamic simulations of a deployable Truss structure with clearances[J]. Chinese Space Science and Technology, 1999, 3: 16-22.

[19] 陈鹿民, 阎绍泽, 金德闻, 等. 含间隙铰空间可展桁架结构的动力学实验[J]. 清华大学学报(自然科学版), 2003, 43(8): 1027-1030.

CHEN Lumin, YAN Shaoze, JIN Dewen, et al. Dynamic experiment of a space deployable truss structure with joint clearances[J]. Journal of Tsinghua University(Science and Technology), 2003,43(8): 1027-1030.

[20] 郝雪清,陈江义.不同运动副材料对间隙机构动力学特性的影响[J].振动与冲击，2012, 31(12): 19-21.

HAO Xueqing, CHEN Jiangyi. Effects of different materials in joints on dynamic characteristics of a mechanism with clearance[J]. Journal of Vibration and Shock, 2012,31(12): 19-21.

[21] 白争锋，赵阳，赵志刚.考虑运动副间隙的机构动态特性研究[J]. 振动与冲击，2011，30(11)：17-20.

BAI Zhengfeng，ZHAO Yang，ZHAO Zhigang. Dynamic characteristics of mechanisms with joint clearance[J]. Journal of Vibration and Shock, 2011,30(11): 17-20.

[22] ZHAO Yang, BAI Zhengfeng. Dynamics analysis of space robot manipulator with joint clearance[J]. Acta Astronautica,2010, 68(7/8):1147-1155.

[23] LIU Caishan, ZHANG Ke, YANG Lei. The compliance contact model of cylindrical joints with clearance[J]. Acta Mechanica Sinica, 2005, 21(5):451-458.

[24] MSC Software, M.S.C. ADAMS®, Release R3, Help System[M]. 2008.

[25] 王旭鹏, 刘更, 马尚君.含间隙运动副机构的动力学特性研究[J]. 振动与冲击, 2016, 35 (7): 110-115.

WANG Xupeng, LIU Geng, MA Shangjun. Study on dynamic characteristics of mechanisms with clearance joint[J]. Journal Vibration and Shock, 2016, 35(7): 110-115.

[26] WANG Xupeng, LIU Geng, MA Shangjun. Dynamic analysis of planar mechanical systems with clearance joints using a new nonlinear contact force model[J]. Journal of Mechanical Science Technology, 2016, 30(4):1537-1545.

Effectsofclearancejointonimpactdynamiccharacteristicsofplanarmechanisms

WANG Xupeng1, LIU Geng2， MA Shangjun2, TONG Ruiting2， XUE Yanmin1

(1. Department of Industrial Design, Xi’an University of Technology, Xi’an 710054, China;2. Shaanxi Engineering Laboratory for Transmissions and Controls, Northwestern Polytechnical University, Xi’an Shaanxi，710072, China)

Here, the effects of clearance joint on impact dynamic characteristics of planar mechanisms were studied. At first, a line-contact impact joint model with axial sizes was established. Based on an improved nonlinear normal impact force model and a modified tangential Coulomb friction force model, the effect laws of clearances on impact dynamic characteristics of a planar slider-crank mechanism were studied through analyzing slider acceleration, clearance joint’s contact force, acceleration frequency spectra and velocity-acceleration phase diagram under different clearances. The results showed that the larger the clearance, the bigger the oscillation amplitude of the mechanism’s dynamic characteristics, and the lower the oscillation frequency; the larger the clearance, the more nonlinear the mechanism’s dynamic characteristics.

nonlinear impact force model; clearance joint; impact dynamics

国家自然科学基金(51275423；51505381);西安理工大学博士启动基金(106-400211001)；西安理工大学校基金(106-256211408)

2016-04-22 修改稿收到日期：2016-06-21

王旭鹏 男，博士，高级工程师，1981年10月生

刘更 男，博士，教授，博士生导师，1961年4月生

TH112

： A

10.13465/j.cnki.jvs.2017.17.012