基于多尺度时不可逆与t-SNE流形学习的滚动轴承故障诊断

姜战伟， 郑近德， 潘海洋， 潘紫微

(安徽工业大学 机械工程学院，安徽 马鞍山 243032)

基于多尺度时不可逆与t-SNE流形学习的滚动轴承故障诊断

姜战伟， 郑近德， 潘海洋， 潘紫微

(安徽工业大学 机械工程学院，安徽 马鞍山 243032)

为了精确地提取机械振动信号的非线性故障特征，提出了一种新的振动信号复杂性测量方法——多尺度时不可逆。同时结合t-分布邻域嵌入(t-SNE)流形学习和粒子群优化-支持向量机(PSO-SVM)，提出了一种新的滚动轴承故障诊断方法。采用多尺度时不可逆提取复杂振动信号的特征信息；利用t-SNE对高维特征空间进行降维；将低维特征向量输入到基于PSO-SVM多故障模式分类器中进行识别与诊断。将提出的方法应用于试验数据分析，并与现有方法进行了对比，分析结果表明，该方法不仅能够有效地诊断滚动轴承的工作状态和故障类型，而且优于现有方法。

多尺度时不可逆；t-分布邻域嵌入；支持向量机；滚动轴承；故障诊断

滚动轴承的振动信号往往是非平稳、非线性的复杂信号，从振动信号中提取非线性特征信息是滚动轴承故障诊断的关键。对于非线性系统产生的时间序列，与分形特征类似，复杂性已成为时间序列的一个基本属性。许多衡量机械动力学系统的非线性时间序列复杂性的方法，如K熵，近似熵[1-2]、样本熵[3-4]、排列熵[5-6]和模糊熵[7-8]等陆续被提出，并被应用于机械振动信号复杂性特征的提取。如Cui等[2]通过提取振动信号经局域波分解后的近似熵来反映滚动轴承故障的复杂性特征变化；Zhu[4]通过提取经验模态分解后本征模态函数的包络样本熵，实现了滚动轴承的故障诊断；Zheng等[9]将局部特征尺度分解与模糊熵结合，提取滚动轴承的故障特征信息等，都取得了不错的效果。

但是，基于熵的算法只能通过测量重复模式的出现(模板匹配)来反映时间序列的规则度，即复杂性的损失表明有较大的周期性[10]。因此随着随机程度增大而单调增高。然而，研究发现，规则度和复杂度之间并没有直接的一一对应关系，复杂度伴随着更丰富的结构[11]。因此，那些赋予不相关随机信号高值的算法并不能真实反映非平衡系统根本的动力学特征。

为了避免熵测量的上述不足，文献[12-14]提出了时不可逆(Time Irreversibility, TI)算法。TI是指信号在时间序列反向操作下，其缺乏统计特征的不变性[12-17]。换言之，信号在时间反向操作下如果其统计特性是不变的，则信号的时间序列具有可逆性，它提供了一种有效的方法来测量非平衡系统的复杂度和反映时间序列的方向性[18]。由于TI评价指标有多种，选择合适的指标提取时间序列的不可逆性特征非常重要。Porta’s指标和Guzik’s指标具有很好的统计特性[19-21]，可以组合评价时间序列不对称性。论文在对时间序列多尺度化的基础上，同时结合多尺度思想，提出了基于上述指标的多尺度时不可逆(Multiscale Time Irreversibility, MSTI)，用来提取时间序列在不同尺度下复杂性信息。

论文考虑将MSTI用于滚动轴承故障振动信号的特征信息提取。由于原始时间序列在进行粗粒化提取不对称特征时故障特征维数过高，很多有效信息被淹没，难以被有效利用。因此，需要采用合适的方法对高维数据进行降维。流形学习是一类借鉴了拓扑流形概念的降维方法，分为线性流形学习算法和非线性流形学习算法。在实际情况下，高维数据往往具有非线性结构，许多非线性流形学习算法，如等距映射(Isometric Mapping, Isomap)[22]，Sammon映射(Sammon mapping)[23]、局部线性嵌入(Locally-linear Embedding，LLE)[24]等非常适合处理这类信号。最近，文献[25]提出了一种深度学习的非线性流形学习算法——t-分布邻域嵌入算法(t-Distributed Stochastic Neighbor Embedding，t-SNE)[25-28]，并且得出了t-SNE在降维效果上要优于Isomap、Sammon mapping和LLE的结论。因此，论文考虑将t-SNE应用于滚动轴承故障特征的降维。

基于上述分析，提出了一种基于MSTI、流形学习t-SNE降维算法和粒子群优化-支持向量机(Particle Swarm Optimization-Support Vector Machine, PSO-SVM)[29-30]的滚动轴承故障诊断新方法。将提出的方法应用于仿真和滚动轴承试验数据分析，结果表明，论文提出的方法能够成功诊断滚动轴承故障的不同状态，是一种有效的故障诊断方法。

1 多尺度时不可逆

1.1多尺度时不可逆算法

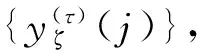
(1)

式中：τ表示尺度因子。对于尺度(τ=1)，时间序列{y1}就是原始时间序列，对于给定的τ，原始时间序列被分割成长度为N/τ的粗粒化序列。

通过计算粗粒化时间序列{yτ}两个临近点之间的差(yτ(k+1)-yτ(k))来获得相应Δyτ的序列。由于不对称序列增加的量(Δyτ>0)等于减少的量(Δyτ<0)。有如下三个指标来测量不对称性。

(1) Porta’s指标，该指标基于估计Δy≠0的总数中Δy(Δy-)小于0的百分比。计算式为

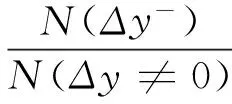
(2)

该指标范围为从0到100。不对称指标P%>50说明Δy-的量比Δy+多。

(2) Guzik’s指标，该指标基于估计所有Δy的累加平方值中正的Δy(Δy+)的平方和的百分比。表达式为

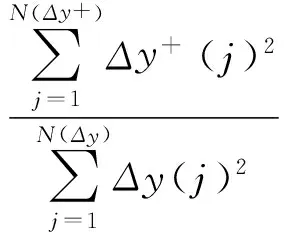
(3)

该指标范围为从0～100。不对称指标G%>50说明|Δy+|的平均量比|Δy-|大，而且Δy的分布偏向正值。

(3) Costa’s指标，该指标根据式(4)估计增量和减量百分比之间的差：

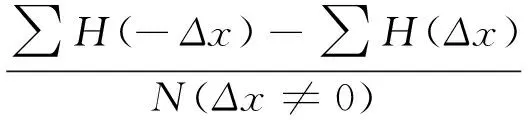
(4)

式中：H是Heaviside函数(当a≥0时，H(a)=1；当a<0时，H(a)=0)，当A=0时，时间序列是对称的。否则，A偏离0越大，相应的时间序列越不可逆。

但是Costa’s指标可以表示为：A=P--P+=2P-1，这里，P-=P%/100。所以本文只考虑Porta’s指标和Guzik’s指标。然而，通过单一尺度数量化多尺度不对称是不合适的，所以通过分别计算每一尺度的P%和G%的平均值作为多尺度不对称。

(5)

(6)

式中，L表示最大尺度。

根据Pm%和Gm%的定义可知，Pm%或Gm%偏离50越大，相应的时间序列越不可逆。然而，当Pm%=50和Gm%=50说明相应的序列是时对称的。

对于一系列时间尺度，计算各个尺度的不对称值的总和，就可以定义多尺度不对称指标AI

(7)

多尺度时不可逆指标算法步骤如下：

(1) 对于有限频率的采样时间序列{x1,x2,…,xi,…,xN},1≤i≤N。对于给定的尺度因子τ=1,2,…,L，根据式(8)

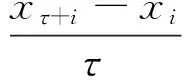
(8)

构造粗粒时间序列；

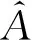
(3) 根据式(9)计算各个尺度的不对称值的总和作为多尺度时不对称指标AI。

(9)

MSTI通过衡量多重尺度时间序列的时不可逆特性，提供了一种新的途径来测量非平衡系统在不同尺度下的复杂度。很适合处理由于轴承在刚度、摩擦和载荷条件等发生瞬态变化时引起机械系统产生的非线性、非平稳振动信号。

1.2仿真信号分析

为了直观地观察多尺度时不可逆分析效果，分别对高斯白噪声与1/f噪声进行多尺度时不可逆仿真分析。两者的数据长度都为5 000，尺度L取20。图1(a)和(b)分别为高斯白噪声波形和1/f噪声波形，图2为高斯白噪声和1/f噪声的多尺度时不可逆测量，由多尺度时不可逆知，在确定某个尺度下，其不对称值离零点越近，则在该尺度下越具有对称性，反之，不对称值离零点越远，则在该尺度下越不具有对称性。且从图2 中看出，白噪声不可逆值几乎所有尺度都在50附近，而1/f噪声随着尺度因子的增大逐渐远离50，这说明了高斯白噪声对称性较强，所包含的信息较少，结构较简单。而1/f噪声时不对称性较强，所包含的状态信息比高斯白噪声信号要复杂的多，结构较复杂。

2 基于MSTI、t-SNE和PSO-SVM的滚动轴承故障诊断方法

滚动轴承的振动信号往往是非平稳和非线性的复杂信号，正常滚动轴承的振动信号是复杂的随机振动，当滚动轴承发生故障时，振动出现规律和周期性的摩擦或冲击，这导致机械系统振动的对称性增加，时不对称性降低。对于不同的故障类型和故障程度，引起的摩擦和冲击的频率和幅度不同，相应地振动信号的复杂性也不同。MSTI具有非平衡系统的基本性质，因此，非常适合处理非平稳、非线性振动信号。在得到振动信号的MSTI故障特征之后，由于特征向量的维数较多，直接用分类器进行模式识别，不但影响分类效率，而且高维数据掩盖了有效信息。因此，采用t-SNE流形学习算法对特征向量矩阵进行降维，挖掘出具有内在规律的低维向量矩阵。为了实现智能诊断，采用训练速度快，适合小样本分类的支持向量机进行模式识别，然而支持向量机的分类结果往往受到惩罚因子c和核函数参数g的影响较大，所以有必要对支持向量机的参数进行优化。粒子群优化算法(Particle Swarm Optimization,PSO)是一种基于群体智能的演化计算技术，通过粒子在解空间搜寻最优值达到寻优的目的，而且能够得到全局最优解，很适合对参数进行优化。利用PSO算法对SVM中的c和g进行优化，建立基于PSO-SVM的多类模式分类器。因此，将降维后的低维特征向量矩阵输入基于PSO-SVM的多类模式分类器进行模式识别。

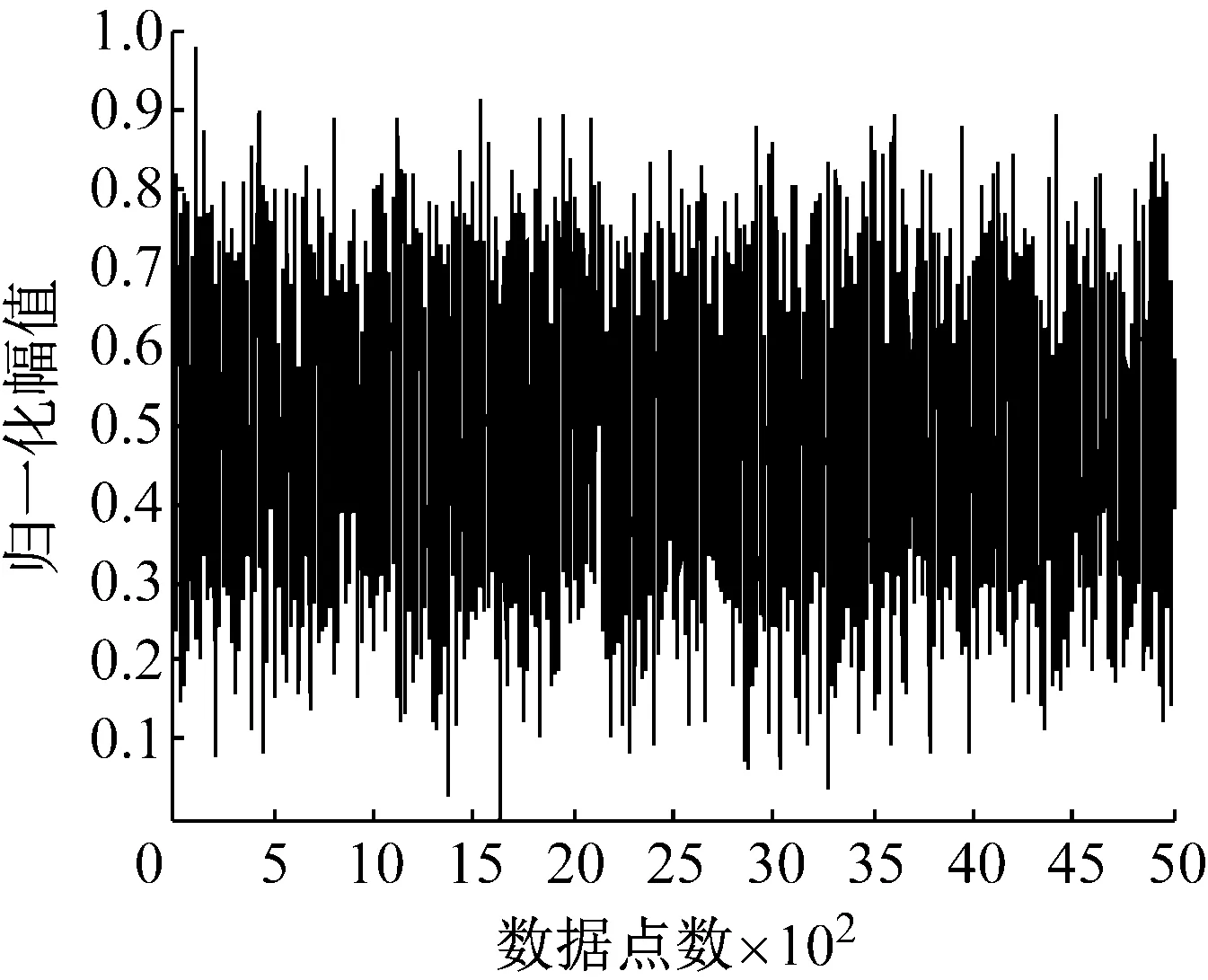
(a) 高斯白噪声波形

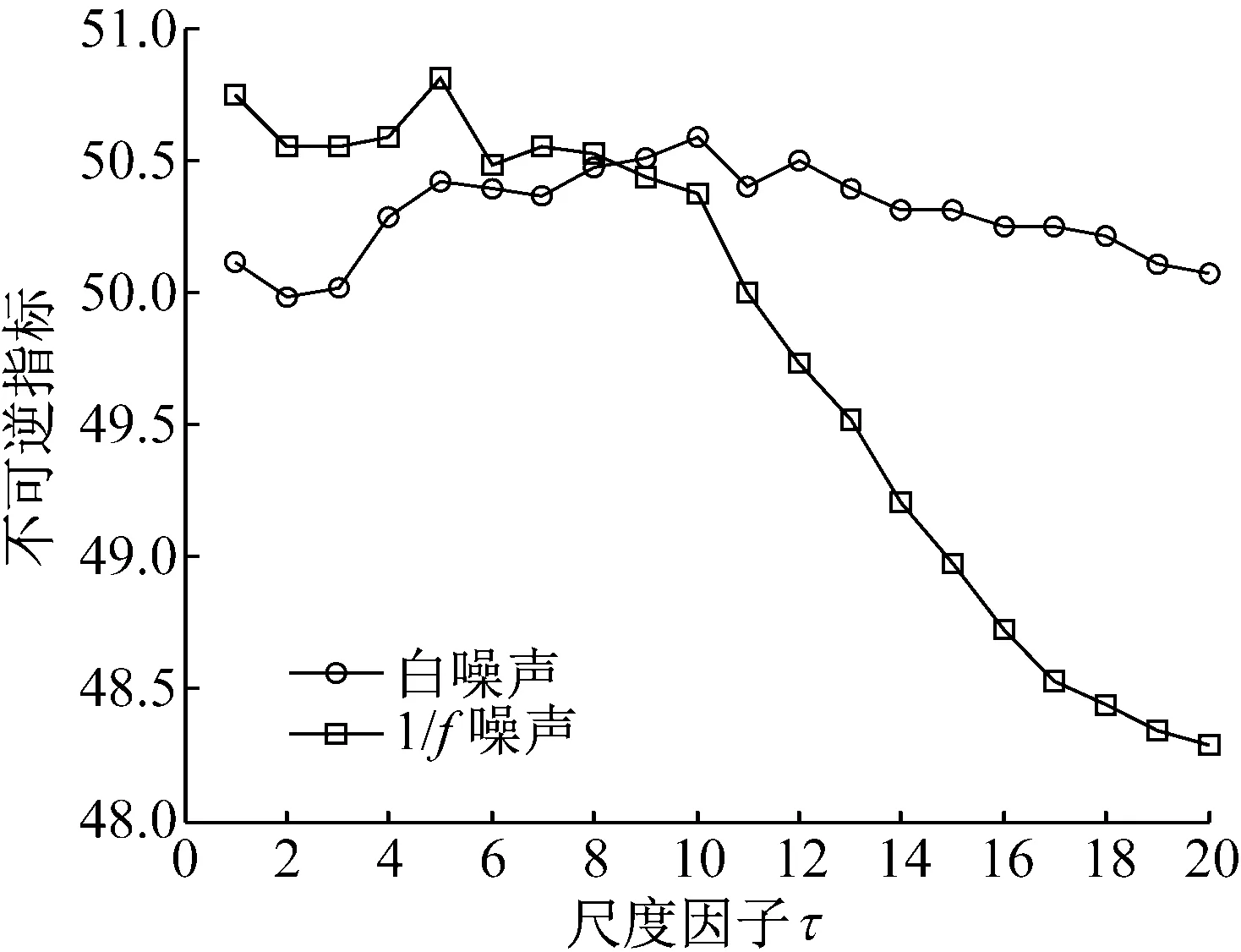
图2 高斯白噪声和1/f噪声的不对称指标

2.1t-SNE流形学习算法

t-SNE流形学习算法是一种深度学习的非线性流形学习算法，它可以有效地实现高维数据的可视化降维。t-SNE主要基于如下思想：如果两个数据点在原始空间中距离较近，但它们的两个映射点距离较远，它们就会相互吸引;当它们的两个映射点距离较近，则他们会相互排斥。当达到平衡时得到最后的映射，完成原始高维空间与低维映射空间之间的映射关系。

在t-SNE算法中代价函数的使用不同于SNE，主要在两个方面：① t-SNE使用简化梯度的对称SNE代价函数；② 它使用t-学生分布代替高斯分布来计算低维空间两点间的相似性。t-SNE利用在低维空间的重尾分布来减缓SNE的聚集和优化问题。

t-SNE算法步骤如下：

(1) 由原始数据序列X={x1,x2,…,xn}，根据式(10)计算复杂度Perp亲疏对Pj|i，其中复杂度Perp为代价函数参数。

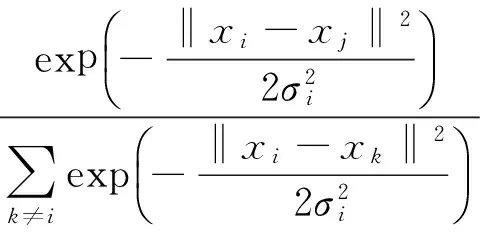
(10)

式中，σi是数据点xi的高斯方差。

(3) 根据式(11)计算低维亲疏qij

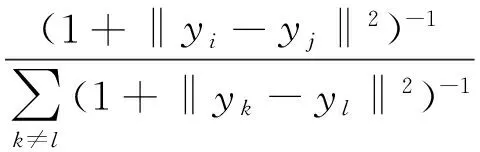
(11)

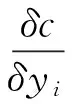
(12)

(5) 根据式(13)得到低维数据

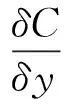
(13)

式中：学习率η，动量α(t)为优化参数。

(6) 迭代循环(3)～(5)，直到t从1到T，最后得到低维数据y(T)={y1,y2,…,yn}。

t-SNE是一种深度学习非线性降维算法，能够从高维数据中恢复低维流形结构，即找到高维空间中的低维流形，并求出相应的嵌入映射，以实现维数约减与数据可视化。

2.2.1 基于MSTI、t-SNE和PSO-SVM的滚动轴承故障诊断方法

基于MSTI、t-SNE流形学习和PSO-SVM的滚动轴承故障诊断方法步骤如下：

(1) 假设滚动轴承的运行状态包含K种类型，每种状态采集N组样本；

(2) 提取每类原始振动信号的MSTI，每组样本得到τ个时不可逆特征值，组成高维特征向量集：RN×τmax，τmax是MSTI算法中最大尺度因子，一般取20；

(3) 采用t-SNE流形学习算法对高维特征向量矩阵进行降维，设定参数，通过特征降维，得到低维敏感特征集：RN×i。

(4) 每种状态各取N/2组组成训练样本，将训练样本输入到基于PSO-SVM多类模式分类器进行训练；

(5) 其余的作为测试样本，用训练好的PSO-SVM对测试样本进行分类，根据PSO-SVM分类器的输出结果确定滚动轴承的工作状态和故障类型。

2.2.2 实验验证

为了验证本文所提出方法的有效性，将其应用于试验数据分析。试验数据采用美国Case Western Reserve University的滚动轴承试验数据[31]。测试轴承为6205-2RSJEM SKF深沟球轴承，使用电火花加工技术在轴承上布置单点故障。考虑转速1 730 r/min、负载3HP条件下正常以及转速1 730 r/min、负载3HP条件下，故障直径大小与深度分别为0.177 8 mm和0.279 4 mm的外圈、内圈和滚动体故障的滚动轴承振动信号。采样频率为12 kHz，采集到具有局部单点点蚀的内圈(Inner Race Fault, IRF)、外圈(Outer Race Fault, ORF)、滚动体故障(Ball Element Fault, BEF)和正常(Normal,NOR)四种状态的振动信号，每种状态取29组数据，每组数据长度为4096，四种状态轴承的振动信号时域波形如图3所示，由于背景环境的影响，从时域波形上很难区别四种状态。将提出的方法应用于实验数据分析，具体步骤与分析如下：

首先提取每类振动信号的MSTI，每种状态取29组样本，每组样本得到20个特征值，四种状态共得到116组样本，组成原始特征向量矩阵：R116×20，其中，τmax取20。

各状态的多尺度Gm%和Pm%值如图4(a)和(b)所示，在图(a)中，在各个尺度下三种故障的Gm%值差别很明显，而且外圈故障的Gm%值随着尺度的增加先增大后减小，在大尺度时稳定在50以上，这说明|Δx+|的平均量级比|Δx-|大；滚动体故障的Gm%值随着尺度的增加一直减小，最后在大尺度时稳定在50以下，说明|Δx+|的平均量级比|Δx-|小；内圈故障的Gm%值随着尺度的增加几乎稳定在50，说明|Δx+|的平均量级和|Δx-|相当；而图(b)中，在各尺度下内外圈故障几乎无法区分且Pm%都维持在50附近，而滚动体故障的Pm%在各尺度下都在50以下。

从图4(a)和(b)中看出，正常滚动轴承的Pm%和Gm%值在小尺度因子时，远离其值50%，随着尺度因子增加，逐渐靠近不对称值50%，最后稳定在50以下，这说明了当滚动轴承发生故障时，由于周期性脉冲减弱了故障振动信号的不对称性，越靠近Pm%和Gm%值的50%，其不对称性越弱，时间序列在反向操作时，其统计特征越具有不变性。单尺度不能够区别故障之间的内在对称特征，只有当进行多尺度化时，故障之间的对称性特征的差别才能够充分表现出来。正常滚动轴承具有较强的不对称性，但由于粗粒化时采取的是线性光滑化和原始时间序列的提取，这导致仅仅捕获粗尺度上的低频成分，损失了细尺度上的高频成分，而高频成分往往包含了更多的时不可逆特征信息，这导致随着尺度的增加，对称性增强。

图3 四种状态轴承振动信号的时域波形

Fig.3 Time domain waveform of the vibration signals of 4 kinds of state bearings (from top to bottom: NOR, ORF, IRF, BEF)

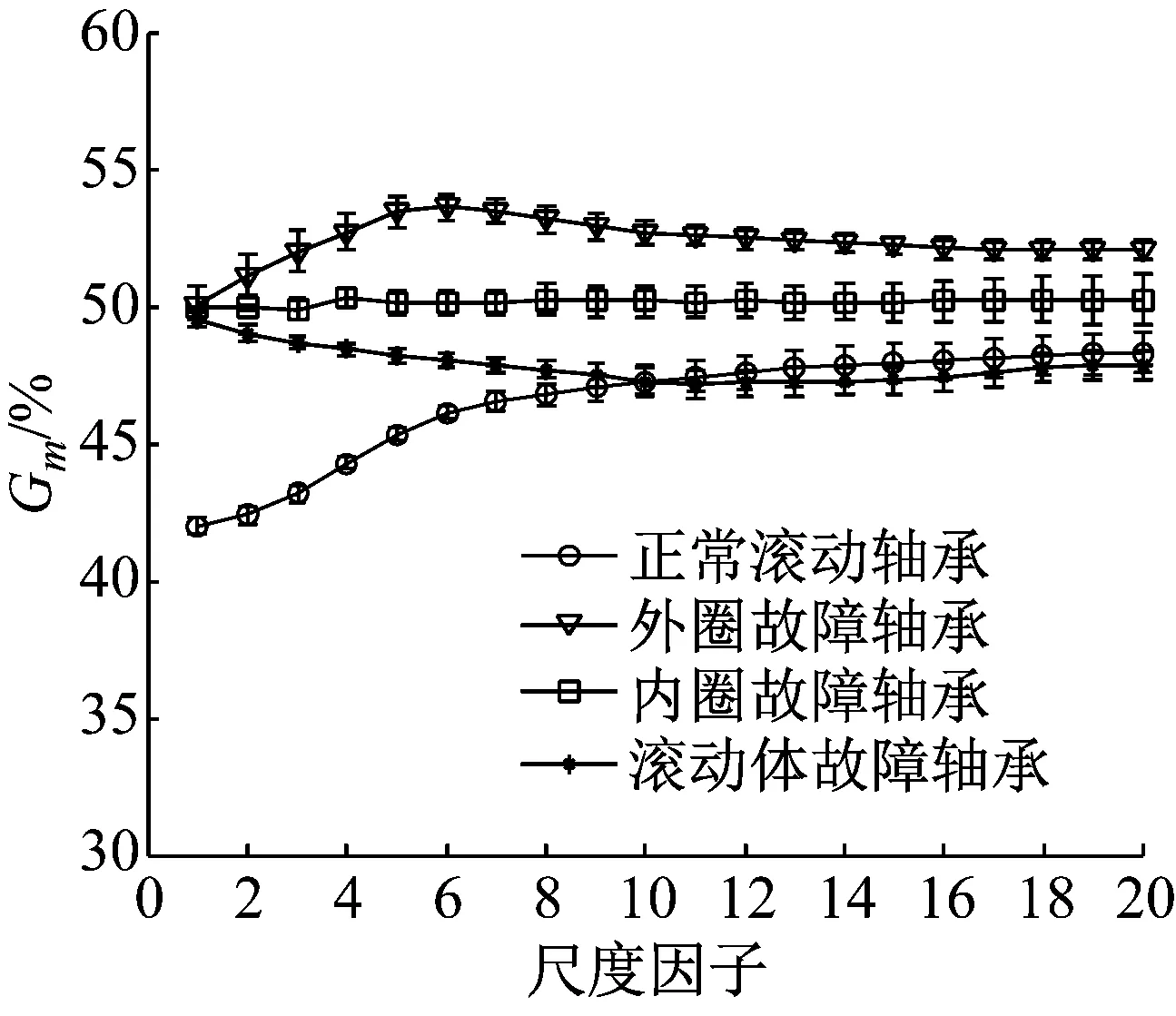
(a) 指标

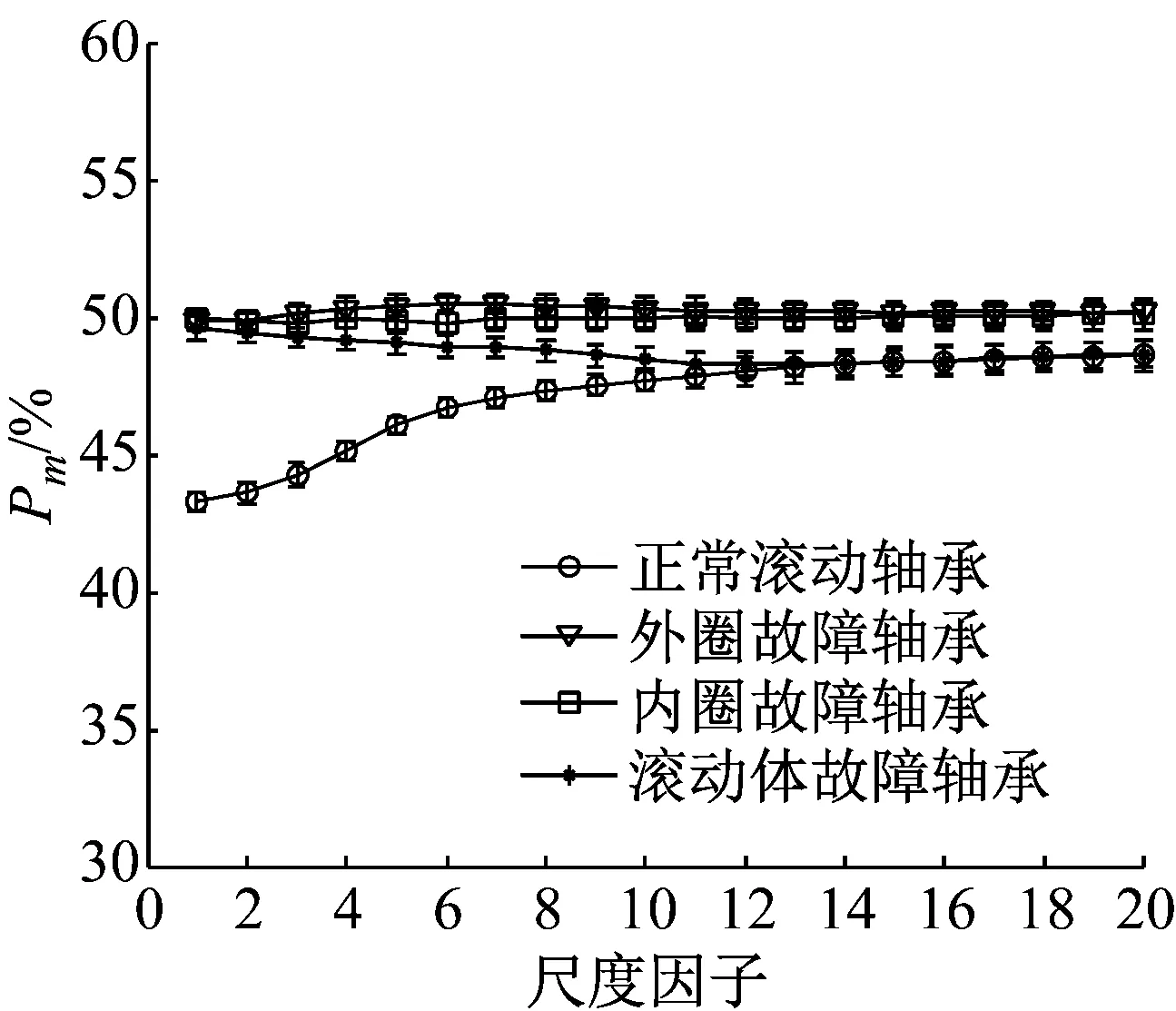
(b) 指标

正常轴承和故障轴承的多尺度Gm%和Pm%值曲线及以上分析说明：正常轴承振动信号时不可逆性较强，结构较复杂；而故障轴承振动信号时不可逆性较弱，结构较简单，这类似于1/f噪声信号和白噪声信号。

各类29组样本的不对称性指标如图5所示，从图5中可以看出，正常滚动轴承振动信号的不对称指标大于故障轴承振动信号的不对称指标，内圈故障的不对称指标几乎关于原点对称，外圈和滚动体故障的不对称指标偏离原点，但仍然在原点附近。此外，29组正常滚动轴承振动信号的不对称指标为AI=-0.696 9±0.086 9(均值标准差)，外圈故障振动信号的不对称指标为AI=0.474 8±0.076 1，内圈故障振动信号的不对称指标为AI=0.030 6±0.106 9，滚动体故障振动信号的不对称指标为AI=-0.432 3±0.067 3。从各类时不对称量化指标可知，正常滚动轴承比故障轴承振动信号的时不对称指标显著地高，外圈故障比内圈和滚动体故障振动信号时不对称指标高，滚动体故障比内圈故障轴承振动信号时不对称指标高，这说明了正常滚动轴承振动信号在时间序列反向操作下其统计特性可变性较强，而故障滚动轴承振动信号的时不可逆性较弱，进一步说明了正常滚动轴承比故障滚动轴承的振动信号复杂的多，从不对称量化指标也可知三种故障之间的区分也比较明显。这也符合一般性的概念，通过多重时间尺度可知，时不可逆会随着故障的发生而降低。

图5 正常轴承、外圈故障、内圈故障和滚动体

Fig.5 Asymmetry index of normal bearing, outer race fault, inner race fault and rolling element fault

以上分析说明了随着尺度的增加时间序列的长度不断减少，在序列长度太短时导致时不可逆性的损失，即在时间序列反向操作下，其缺乏统计特征的可变性。所以正常滚动轴承的值Gm%和Pm%值会随着尺度的增加而逐渐趋向50。而且在衡量序列时不可逆Gm%值比Pm%值区分故障振动信号效果更好。

为了说明t-SNE方法进行特征降维的必要性和优越性，将其与Isomap方法、Sammon mapping方法进行对比，三者降维后得到的样本二维和三维分布图如图6所示。从图6(a)和图6(b)可以很明显地看出，采用t-SNE方法进行特征降维后四种状态的二维和三维特征分布分的很开，没有混淆现象。而从图6(c)和图6(d)看出，采用Sammon mapping方法降维后，四种状态的三维特征分布靠的很近，特别是内圈故障与外圈故障混淆在一起，从二维特征分布也明显看出，三种故障有交叉混叠现象。从图6(e)和图6(f)也很清楚地看出，采用Isomap特征降维后，导致三种故障三维特征分布特征分布很靠近，内圈故障和外圈故障有交叉混叠。经过对比可知，t-SNE方法比Sammon mapping和Isomap方法更能提取用于区分样本的敏感特征。上述分析结果表明了t-SNE方法进行特征降维的优越性。

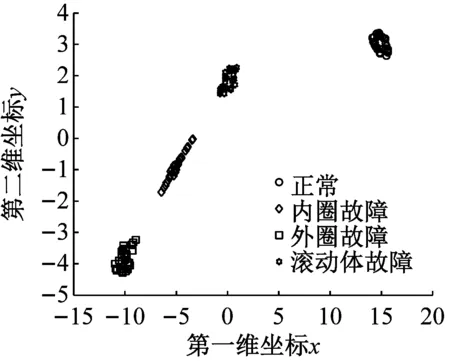
(a) t-SNE二维分布

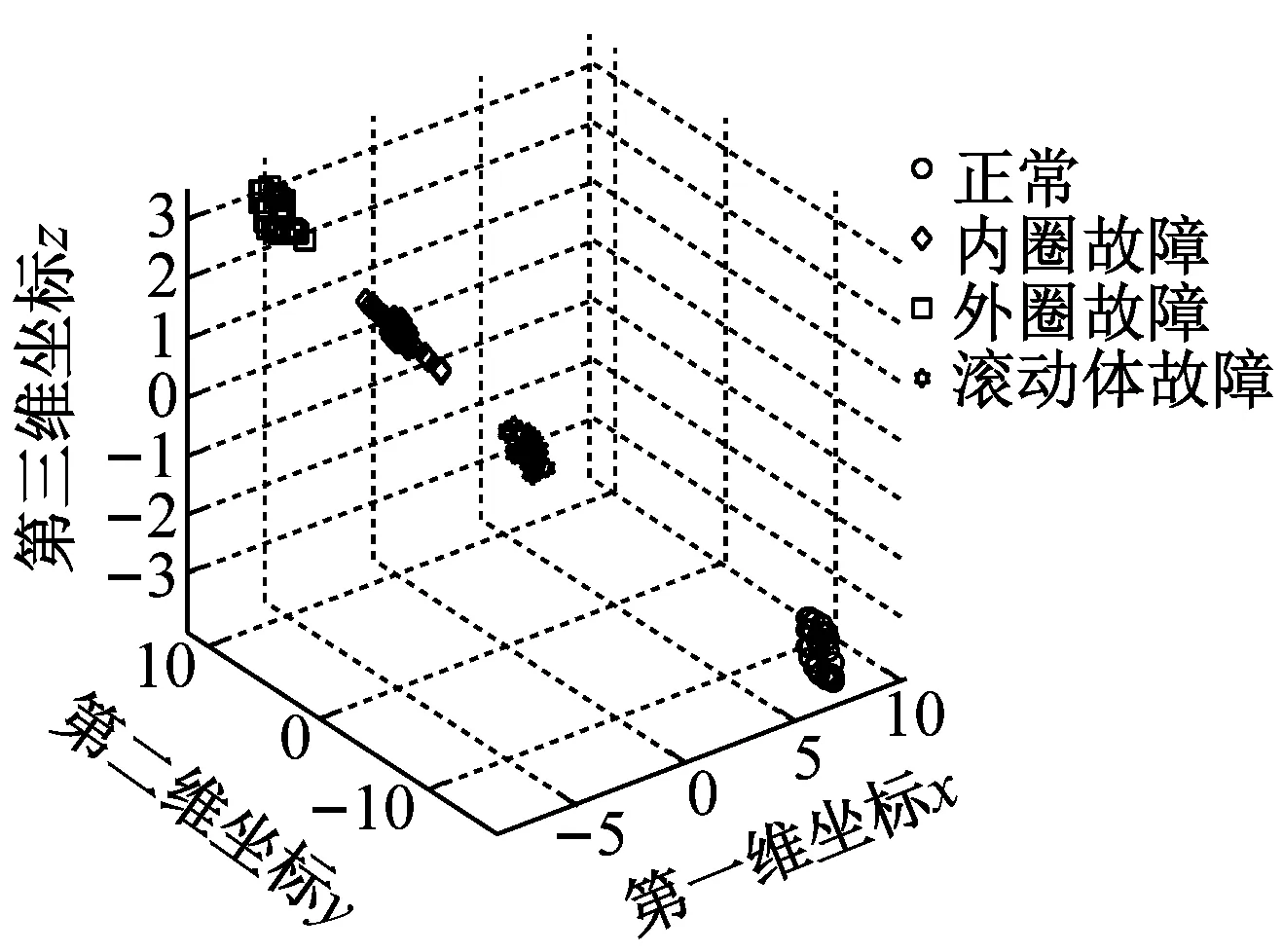
(b) t-SNE三维分布

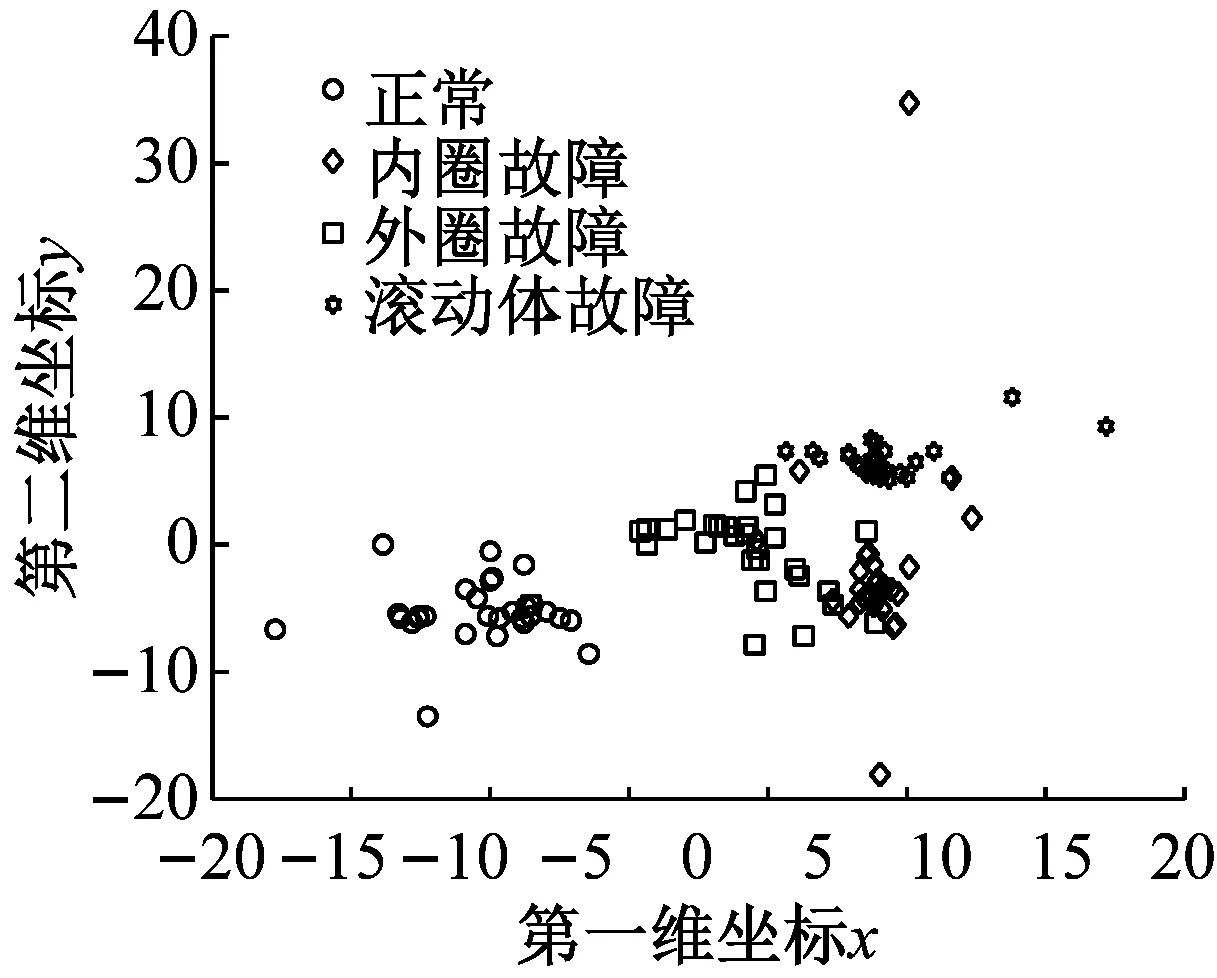
(c) Sammon mapping二维分布

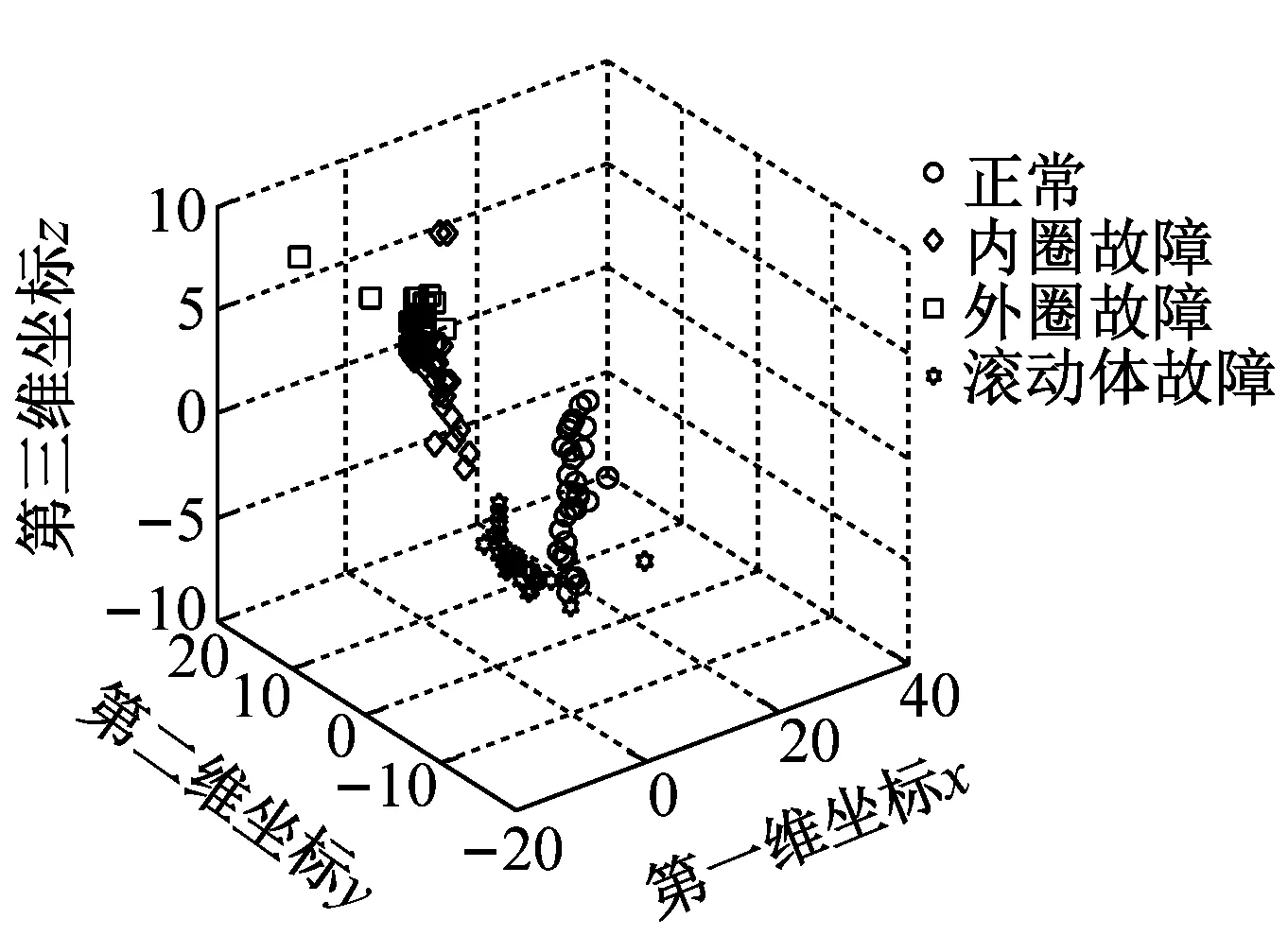
(d) Sammon mapping三维分布

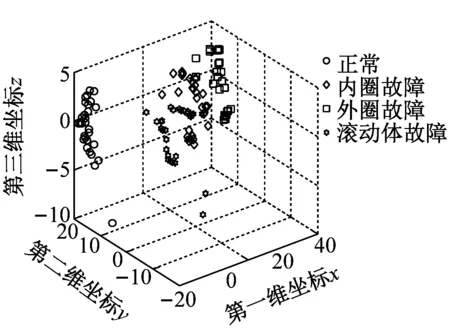
(e) Isomap三维分布

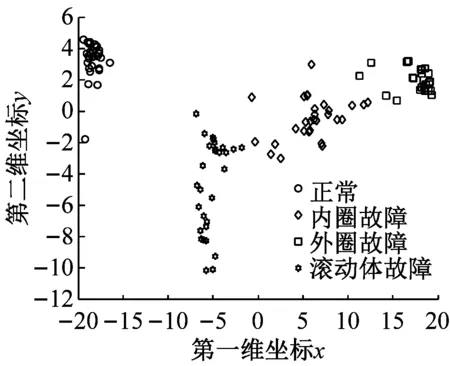
(f) Isomap二维分布

然后，设定嵌入维数d=3，采用t-SNE方法对高维特征向量空间进行特征降维，得到低维特征向量集：R116×3。再次，每种状态取15组构成训练样本特征集：R60×3，采用训练样本特征集对基于PSO-SVM多类模式分类器进行训练，由于SVM是二分类器，采用“一对一”的方式建立多故障分类器。其中用粒子群优化算法优化SVM中惩罚参数c和核函数参数g，对训练样本特征集进行交叉验证意义下的识别率作为PSO中的适应度函数值，设定PSO算法中的局部搜索能力c1为1.5，全局搜索能力c2为1.7，种群数量为20，迭代次数为200。搜索到的最佳惩罚因子c为0.1，核函数参数g为59.566 7。

用训练好的PSO-SVM多模式分类器对测试样本特征集进行分类预测。根据PSO-SVM分类器的输出值确定滚动轴承的工作状态和故障类型，其中，1表示正常，2表示外圈故障，3表示内圈故障，4表示滚动体故障。预测样本输出结果如图7所示。从图7中可以看出所有测试样本类别都得到了准确的分类，论文提出的方法对测试样本集的识别率达到100%，这说明了论文方法的有效性。

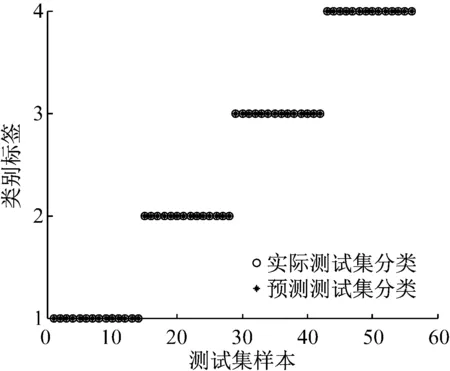
图7 论文方法的输出结果

为了将本文特征提取方法与传统的特征提取方法进行比较，提取各状态原始振动信号的峭度、复杂度[32]和模糊熵特征值，各状态样本数、数据长度以及训练样本数和测试样本数与本文上述提出的方法相同，然后将提取的特征值分别输入到基于PSO-SVM的多故障多模式分类器中进行模式识别，其SVM参数优化结果及分类结果如图8(a)和图8(b)所示。从图8(b)可以看出有两个内圈故障样本被错误地分到了外圈故障中，其正确识别率为96.428 6%低于本论文提出的方法。

适应度曲线Accuracy[PSO method]

(参数c1=1.5，c2=1.7，终止代数=200,种群数量pop=20)

Best c=0.1 g=210.770 2 CVAccuracy=100%

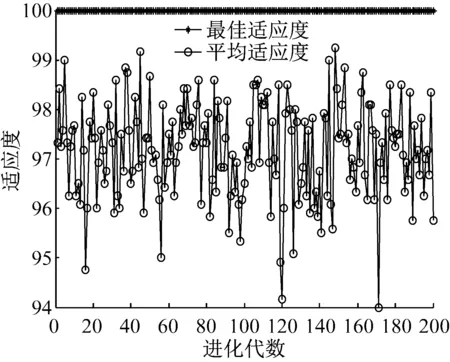
(a) SVM参数优化结果

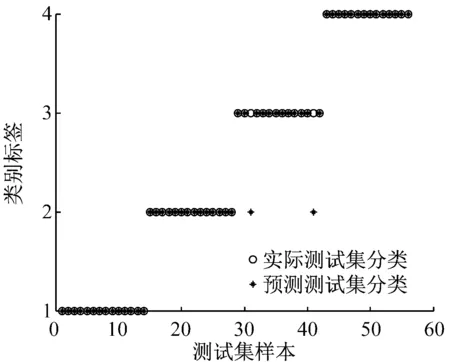
(b) SVM参数优化后分类结果

为了说明PSO参数优化的优越性，再采用Isomap降维的低维特征向量空间分别输入基于SVM和PSO-SVM的多模式分类器进行训练与测试，其SVM分类结果和PSO-SVM参数优化与分类结果如图9、图10(a)和图10(b)所示。从图9可以看出，采用Isomap方法进行特征空间降维后，SVM未进行参数优化时，故障识别率为96.428 6%，而通过对SVM进行参数优化选择，寻优得到最佳惩罚因子和核函数参数组合为[2.586 4,16.899]，识别率提高到了98.214 3%，但未达到采用t-SNE算法得到的100%识别率。这说明了SVM通过PSO参数优化，选择了最佳参数组合，避免了人为因素的干扰，提高了分类精度。

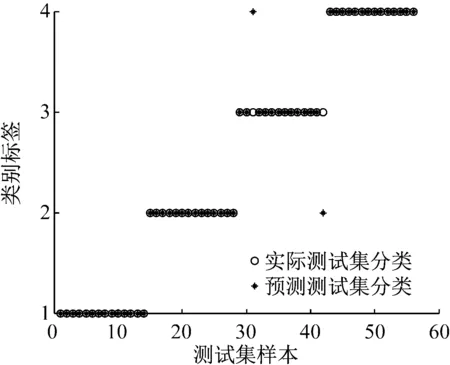
图9 SVM参数未优化分类结果

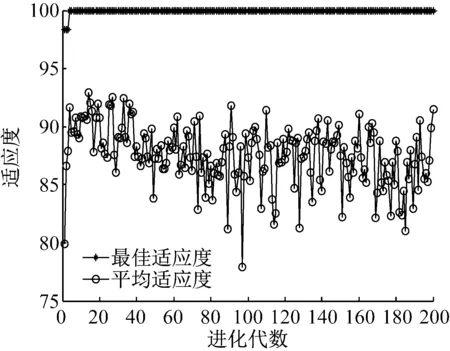
(a) SVM参数优化结果

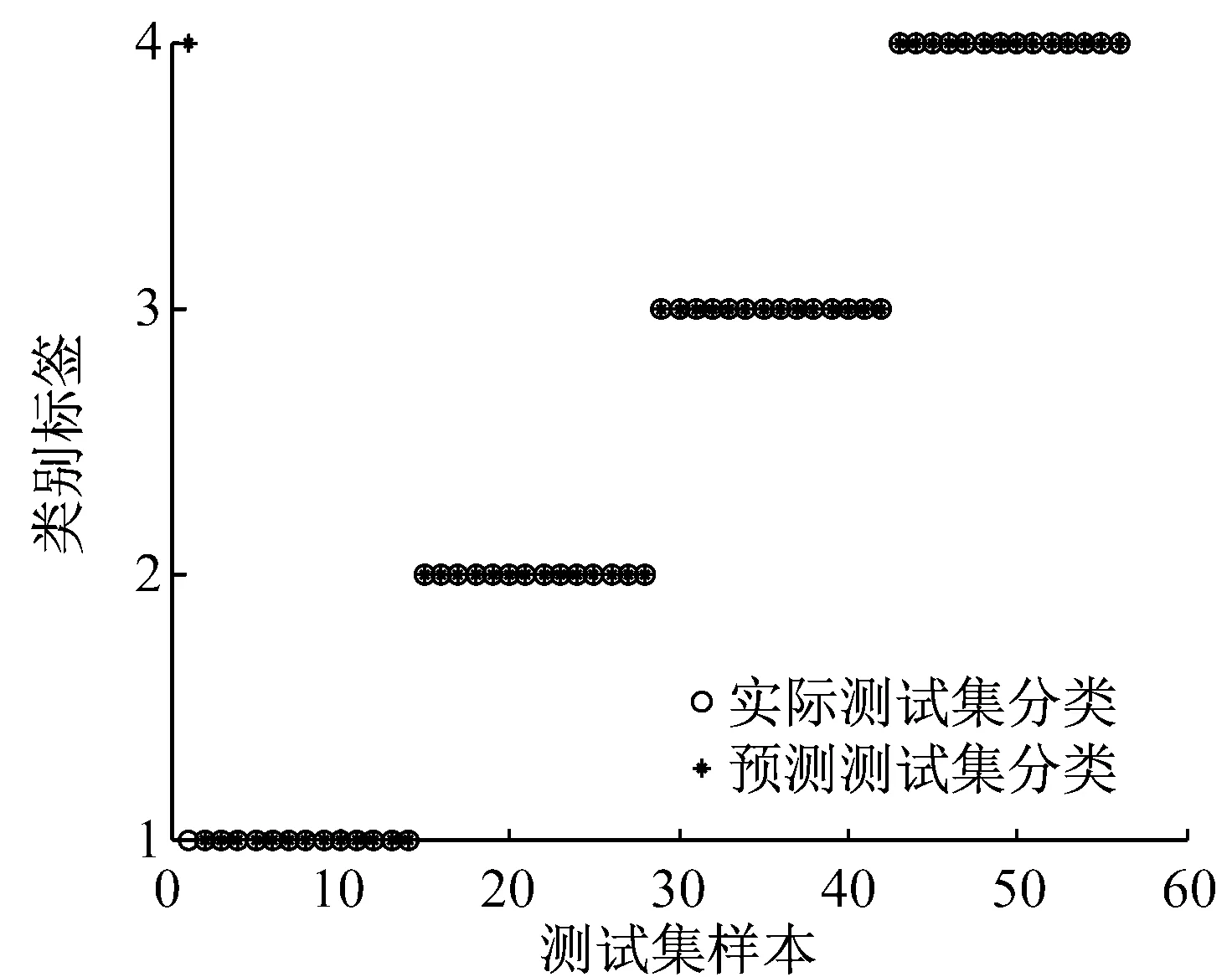
(b) SVM参数优化后分类结果

3 结 论

(1) 提出了一种新的衡量机械系统非线性、非平衡复杂信号特征的方法——多尺度时不可逆，并与传统特征提取方法进行了对比，结果表明MSTI可以提取传统方法不能提取的特征信息。

(2) 将t-SNE流形学习方法应用于滚动轴承故障特征的降维，得到具有内在规律性的低维可视化特征，且保留了信息的本质特征，试验分析结果表明相较于Isomap和Sammon mapping，t-SNE在可视化降维方面更具有优势，更有利于故障的诊断。

(3) 提出一种新的基于MSTI、t-SNE流形学习和PSO-SVM的滚动轴承故障诊断方法，仿真和试验分析结果表明该方法不仅在非线性特征提取，高维特征可视化降维方面有显著的优势，而且在分类效果方面，特别地SVM经参数优化后，识别率有明显的提高。

[1] PINCUS S M. Assessing serial irregularity and its implications for health[J]. Annals of the New York Academy of Sciences, 2001, 954(1):245-267.

[2] CUI B Z, PAN H X, WANG Z B. Fault diagnosis of roller bearings base on the local wave and approximate entropy[J]. Journal of North University of China (Natural Science Edition), 2012, 33(5):552-558.

[3] 何志坚, 周志雄. 基于ELMD的样本熵及Boosting-SVM的滚动轴承故障诊断[J]. 振动与冲击, 2016, 35(18)：190-195.

HE Zhijian, ZHOU Zhixiong. Fault diagnosis of roller bearings based on ELMD sample entropy and Boosting-SVM[J].Journal of Vibration and Shock, 2016, 35(18)：190-195.

[4] ZHU K. Fault diagnosis of rolling bearings based on IMF envelope sample entropy and support vector machine[J]. Journal of Information & Computational Science, 2013, 10(16):5189-5198.

[5] BANDT C, POMPE B. Permutation entropy: a natural complexity measure for time series[J]. Physical Review Letters, 2002, 88(17):174102.

[6] 郝旺身, 王洪明, 董辛,等. 基于全矢排列熵的齿轮故障特征提取方法研究[J]. 振动与冲击, 2016, 35(11):224-228.

HAO Wangshen, WANG Hongming, DONG Xin, et.al. Gear fault feature extraction based on full vector permutation entropy[J].Journal of Vibration and Shock, 2016, 35(11):224-228.

[7] CHEN W, WANG Z, XIE H, et al. Characterization of surface EMG signal based on fuzzy entropy[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2007, 15(2): 266-272.

[8] 舒思材, 韩东. 基于多尺度最优模糊熵的液压泵特征提取方法研究[J]. 振动与冲击, 2016, 35(9):184-189.

SHU Sicai, HAN Dong. Approach for a hydraulic pump’s feature extraction based on multiscale optimal fuzzy entropy.[J].Journal of Vibration and Shock, 2016, 35(9):184-189.

[9] ZHENG J, CHENG J, YANG Y. A rolling bearing fault diagnosis approach based on LCD and fuzzy entropy[J]. Mechanism & Machine Theory, 2013, 70(6):441-453.

[10] COSTA M, GOLDBERGER A L, PENG C K. Multiscale entropy analysis of biological signals[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2005, 71(1):021906-021906.

[11] COSTA M D, PENG C K, GOLDBERGER A L. Multiscale analysis of heart rate dynamics: entropy and time irreversibility measures[J]. Cardiovascular Engineering, 2008, 8(2): 88-93.

[12] COSTA M, GOLDBERGER A L, PENG C K. Broken asymmetry of the human heartbeat: loss of time irreversibility in aging and disease[J]. Physical Review Letters, 2005, 95(19): 198102.

[13] VAN DER HEYDEN M J, DIKS C, PIJN J P M, et al. Time reversibility of intracranial human EEG recordings in mesial temporal lobe epilepsy[J]. Physics Letters A, 1996, 216(6): 283-288.

[14] PORTA A, GUZZETTI S, MONTANO N, et al. Time reversibility in short-term heart period variability[C]//2006 Computers in Cardiology. IEEE, 2006: 77-80.

[15] COX D R, GUDMUNDSSON G, LINDGREN G, et al. Statistical analysis of time series: Some recent developments[with discussion and reply][J]. Scandinavian Journal of Statistics, 1981: 93-115.

[16] DIKS C, VAN HOUWELINGEN J C, TAKENS F, et al. Reversibility as a criterion for discriminating time series[J]. Physics Letters A, 1995, 201(2): 221-228.

[17] CASALI K R, CASALI A G, MONTANO N, et al. Multiple testing strategy for the detection of temporal irreversibility in stationary time series[J]. Physical Review E, 2008, 77(6): 066204.

[18] PRIGOGINE I, ANTONIOU I. Laws of nature and time symmetry breaking[J]. Annals of the New York Academy of Sciences, 1999, 879(1): 8-28.

[19] PORTA A, CASALI K R, CASALI A G, et al. Temporal asymmetries of short-term heart period variability are linked to autonomic regulation[J]. Ajp Regulatory Integrative & Comparative Physiology, 2008, 295(2):R550-7.

[20] PORTA A, GUZZETTI S, MONTANO N, et al. Time reversibility in short-term heart period variability[C]// Computers in Cardiology. 2006:77-80.

[21] GUZIK P, PISKORSKI J, KRAUZE T, et al. Heart rate asymmetry byPoincaré plots of RR intervals[J]. Biomedizinische Technik Biomedical Engineering, 2006, 51(4):272-5.

[22] KRAMER O, LUCKEHE D. Visualization of evolutionary runs with isometric mapping[C]// Evolutionary Computation. IEEE, 2015.

[23] DYBOWSKI R, COLLINS T D, HALL W, et al. Visualization of binary string convergence by sammon mapping[C]. First Student Workshop of the Psychology of Programming Interest Group, 1996：377-383.

[24] ROWEIS S T, SAUL L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500):2323-2326.

[25] LAURENS V D M, HINTON G. Visualizing Data using t-SNE[J]. Journal of Machine Learning Research, 2008, 9:2579-2605.

[26] HINTON G E. Visualizing high-dimensional data using t-SNE[J]. Vigiliae Christianae, 2008, 9(2):2579-2605.

[27] KASKI B S. t-distributed stochastic neighbor embedding[C]// In Proc. 2010.

[28] LAURENS V D M. Accelerating t-SNE using tree-based algorithms[J]. Journal of Machine Learning Research, 2014, 15(1):3221-3245.

[29] SUBASI A. Classification of EMG signals using PSO optimized SVM for diagnosis of neuromuscular disorders[J]. Computers in Biology & Medicine, 2013, 43(5):576-586.

[30] ABDI M J, GIVEKI D. Automatic detection of erythemato-squamous diseases using PSO-SVM based on association rules[J]. Engineering Applications of Artificial Intelligence, 2013, 26(1):603-608.

[31] http://csegroups.case.edu/bearingdatacenter/pages/download-data-file. Bearing Data Center, Case Western Reserve University.

[32] 朱永生, 袁幸, 张优云,等. 滚动轴承复合故障振动建模及Lempel-Ziv复杂度评价[J]. 振动与冲击, 2013, 32(16):23-29.

ZHU Yongsheng, YUAN Xing, ZHANG Youyun, et al. Vibration modeling of rolling bearings considering compound multi-defect and appraisal with Lempel-Ziv complexity[J]. Journal of Vibration and Shock, 2013, 32(16):23-29.

Rollingbearingfaultdiagnosismethodbasedonmultiscaletimeirreversibilityandt-SNEmanifoldlearning

JIANG Zhanwei， ZHENG Jinde， PAN Haiyang， PAN Ziwei

(School of Mechanical Engineering, Anhui University of Technology, Maanshan 243032, China)

In order to accurately extract nonlinear fault features of mechanical vibration signals, a novel method for complexity measurement of vibration signals called the multiscale time irreversibility (MSTI) was proposed. Meanwhile, combining the t-distributed stochastic neighbor embedding (t-SNE) and the particle swarm optimization-support vector machine (PSO-SVM), a new fault diagnosis method for rolling bearings was proposed. Firstly, MSTI was used to extract the characteristic information of complex vibration signals. Secondly, t-SNE was used to reduce dimensions of the high dimension feature space. Then the selected lower dimensional feature vectors were input to a PSO-SVM-based multi-fault classifier for fault diagnosis. Finally, the proposed method was applied in the test data analysis and compared with the existing methods. The analysis results showed that the proposed method can be used to effectively diagnose the working status and fault types of rolling bearings, it is superior to the existing methods.

multiscale time irreversibility (MSTI); t-distributed stochastic neighbor embedding (t-SNE); support vector machine (SVM); rolling bearing; fault diagnosis

国家自然科学基金(51505002;51305046)；安徽省高校自然科学研究重点资助项目(KJ2015A080)；安工大研究生创新研究基金(2016062)

2016-11-22 修改稿收到日期：2016-12-21

姜战伟 男，硕士生，1990年5月生

郑近德 男，博士，硕士生导师，1986年3月生 E-mail:lqdlzheng@126.com

TN911.7；TH165.3

： A

10.13465/j.cnki.jvs.2017.17.010