在活动中生成 在问题中发展——“圆”教学实录与反思

■陈海燕

在活动中生成 在问题中发展
——“圆”教学实录与反思

■陈海燕

为了更好地体现新课程的基本理念，正确理解和把握教学内容，突出数学知识的本质内涵，关注数学知识的形成过程，本节课的框架共分为5个部分。课堂上，学生通过自主动手画圆，理解什么是圆，从而抽象、归纳出圆的定义，同时，教师以问题串来驱动，使学生在愉悦的气氛下较自然地经历了数学知识的形成过程，理解了数学知识的本质内涵，培养了学生数学学习的思维方式和思维习惯。

一、教学实录

1.我们认识的圆是什么样的图形——激活纠偏。

师：同学们请看，这里有没有你熟悉的几何图形？

生（七嘴八舌）：圆。

师：在小学我们就学过圆，现在你对圆有哪些认识呢？

生（七嘴八舌）：圆有圆心、半径，我们还会求圆的面积、周长等。

师：在古代曾有记载“圆，一中同长也”，这是什么意思？圆到底是一个什么样的图形呢？我们先来看这几个问题，问题1：（出示呼啦圈图片。）呼啦圈是圆吗？你还能举出生活中跟圆有关的例子吗？

生1：车轮，满月，红日……

师：生活中的圆处处可见，问题2：（出示篮球图片。）篮球是圆吗？为什么？

生2：不是，圆是平面图形。

师：好，再看问题3：（出示一元硬币图片。）一元硬币是圆吗？牡丹花在圆上吗？

生3：一元硬币是圆，牡丹花在圆上。

生4：一元硬币不是圆，圆好像是线，不是面。

师：那么究竟是不是呢？我们过会儿再来判断。问题4：（出示椭圆图片。）这个图形是圆吗？为什么？

生5：是。

生6：不是，这个图形有点圆圆的样子，但好像又不是那么圆。

师：是不是呢？似乎有点说不太清楚，所以在初中阶段，我们需要对圆做进一步的研究。今天这节课我们就一起来研究圆。（板书：2.1圆。）

评析：教师把要讲的东西形成问题串，以问题串来驱动，用4个问题达到目标，这里每个问题都是有目的，有用意的。问题1，这是正面的例子，让学生感知生活中圆的形象处处可见；问题2，是反例，认识圆是平面图形；问题3，这也是反例，圆不是面，是曲线，认识上的误区引起认知上的冲突，这就是最后我们需要认清的东西；问题4，还是反例，究竟什么是圆呢，得出进一步研究的必要性，从而引出课题。

2.圆是怎样形成的——运动定义。

师：同学们会不会用圆规画圆？下面先请同学们用圆规在作业纸上画一个圆。

活动1：用圆规画圆。（学生动手操作，教师巡视指导。）

师：我来看看同学们画的，画得真不错，画圆最主要是要确定什么？

生7：圆心和半径。

师：老师也想来画一个圆，但是这圆规在白板上不能画怎么办？老师这儿有笔还有绳子，能画圆吗？你们能不能动手试试？

活动2：用一根绳子和笔，在作业纸上作圆。（学生动手尝试，请一位学生在黑板上演示。）

师：厉害啊！利用绳子我们也能画出一个圆，能画出圆的同学请举手。我想问，这个圆是怎样形成的呀？同座位同学可以互相交流一下。

生8：我们可以将这根绳子看成是一条线段，绕着它的一端，旋转一周。

师：那是谁形成的图形？

生9：绳子的另一端。

师：这样我们就得到了圆的定义：我们把平面内线段OP绕着点O旋转一周，端点P运动所形成的图形叫作圆。这是从圆形成的运动的角度来给它下的定义。（板书圆的运动定义。）其中点O叫作圆心，线段OP叫作半径。我们来给这个圆起个名字吧，叫它什么呢？我们通常是以圆心的字母来命名圆的，记作“⊙O”，读作“圆O”。

评析：对于运动定义部分，教师安排了两个活动。学生用圆规画圆，这是对已有知识的回顾，明确圆的两要素：圆心和半径。将绳子拉直了就可以看成是一条线段，用绳子画圆的过程其实就是圆形成的过程。学生自己动手操作，感知圆的运动定义。

3.圆由什么样的点组成——集合定义。

师：刚才我们在作业纸上画了一个圆，现在你在这个平面上再任意画一个点，请同学们思考问题5：平面上任意一点与圆的位置关系有几种呢？

生10：点在圆上，点在圆内，点在圆外。（教师板书。）

师：好，我们来看练习1——说出图中点A、点B、点C与圆的位置关系。

生11：点A在圆内、点B在圆上、点C在圆外。

师：很好，练习2——在图中再画一些圆内的点、圆上的点、圆外的点。哪位同学愿意上黑板来画一画？（学生们在作业纸上画圆内的点，请一位学生在黑板上画。）

师：这样的点还有吗？

生12：有。

师：继续画，还有吗？

生13：有。

师：这样的点多不多？

生14：多。

师：有多少个？

生15：无数个。

师：谁再来画圆上的点？圆上的点有多少个？

生16：无数个。

师：那圆外的点呢？谁来画一画？

生17：圆外的点也有无数个。

师：也就是说，一个圆可将整个平面划分为3个区域：圆的内部、圆上、圆的外部。每个部分都可以看成是由无数个点所组成的。这无数个点就组成了点的集合。下面我们分别来研究这3类点的集合，我们先从最简单的开始——圆上的点，请问：圆上所有点都满足什么条件？

生18：到圆心的距离等于半径。

师：到圆心距离等于半径的点都在哪？

生19：圆上。

师：好，问题6——圆可以看成是满足什么条件的点的集合？

生20：圆是到圆心的距离等于半径的点的集合。（教师板书。）

师：圆心和半径在没有圆的时候能用吗？

生21：不能。

师：所以在这儿我们把它改为定点和定长，这样更规范。这样，我们从集合的角度又给圆下了一个定义：圆是到定点（圆心）的距离等于定长（半径）的点的集合。（教师板书。）

师：现在我们知道圆是由无数个满足一定条件的点组成的，当然这无数个点也就组成了圆，所以圆是一条线？还是一个面？

生22：是一条线。

师：是一条怎样的线？

生23：是一条曲线。

师：怎样的曲线？

生24：首尾顺次相接的封闭的曲线。

师：好，问题7——用上述类似的方法研究圆的内部和圆的外部，你能得出什么结论？

生25：圆内部的所有点到圆心的距离小于半径。

师：咦？这里怎么又改成圆心和半径啦？要想确定圆的内部和外部，首先要有什么呀？

生26：圆。

师：所以在这里我们用圆心和半径，在这个细节上我们感受到了数学的严谨美！我还想问，圆内部的点到圆心的距离为什么小于半径呢？你能用几何的方法说明吗？

生27：在圆的内部任意取一点，设为A，连接OA并延长交⊙O于点C，因为OA＜OC，所以A到圆心的距离小于半径。

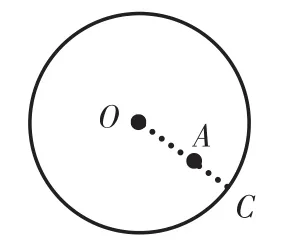
师：反过来，我们又得到——所有到圆心的距离大于半径的点都在圆的外部。那么圆的内部又可以看成是满足什么条件的点的集合呢？

生28：圆的内部是到圆心的距离都小于半径的点的集合。

师：圆的外部呢？

生29：圆的外部是到圆心的距离都大于半径的点的集合。

师：现在你能解决前面的两个问题吗？一元硬币是圆吗？牡丹花在圆上吗？

生30：一元硬币不是圆，圆不是面，是曲线，牡丹花不在圆上，它在圆的内部。

师：那椭圆是圆吗？

生31：不是圆。

评析：圆的集合定义是这节课的难点，为了突破难点，教师让学生自己动手画圆内的点、圆上的点、圆外的点，让他们充分感知每部分都是由无数个点所组成的，感受到点的集合的概念，并提炼出：一个圆可以把整个平面划分为圆的内部、圆上、圆的外部这3个区域。再分别研究这3类点的集合，重点研究最简单的一个——圆上的点，然后类比得出圆的内部、圆的外部的概念。当学生得到结论：圆内部的所有点到圆心的距离都小于半径时，教师并没有满足于学生通过直观感知得到的这一结论，而是希望学生能结合图形简单说理，这种思维对学生以后的数学学习是非常重要的。

4.如何判定点与圆的位置关系——判定定理。

师：任何一个定义其实都有判定和性质两大功能，现在我们尝试用圆的集合定义来寻找判定点与圆位置关系的方法。为了表示方便，我们用r表示圆的半径，用d表示点到圆心的距离，所以圆上的点满足的特征我们可以简洁地表示为：点在圆上，反过来，我们也可以简洁地表示为点在圆上，合起来即为：点在圆上d=r。（教师板书。）

师：对于点在圆内、点在圆外，你是否可以得出类似的结论？

师：现在我们来看这3个结论，等号左边刻画的是点与圆的位置关系，等号右边刻画的是d与r的数量关系。从左到右，是由位置关系推出数量关系，是性质；从右到左，是由数量关系推出位置关系，是判定。二者结合起来，则体现了一种完美的数形结合的思想。

评析：在整体框架中，其实每个部分之间还是有联系的，圆的判定定理就是根据集合定理得到的，教师讲解时仍然是重点讲了点在圆上，推而广之得到点在圆内、点在圆外。最后结论赏析，体现了一种完美的数形结合思想。

5.用结论解决相关问题——交集思想。

例1.已知⊙O的半径为5，点P为平面上的一点。（1）若PO=_____，则点P在圆上；（2）若PO=5.5，则点P在 ；（3）若点P在圆内，则PO的取值范围是 。

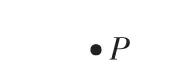
图1

例2.如图1，已知点P，请作出到点P的距离等于1cm的点的集合。（1）这个圆的外部是满足什么条件的点的集合？（2）请用阴影表示出到点P的距离小于或等于1cm的点的集合。

图2

例3.如图2，已知点P、Q，且PQ＝2cm。（1）画出下列图形：到点P的距离等于1cm的点的集合，到点Q的距离等于1.5cm的点的集合；（2）在所画图中，到点P的距离等于1cm，且到点Q的距离等于1.5cm的点有几个？请在图中将它们表示出来；（3）在所画图中，到点P的距离小于或等于1cm，且到点Q的距离大于或等于1.5cm的点的集合是怎样的图形？把它表示出来。

评析：这一环节有3个例题。例1是一个简单的实例，让学生对由数量关系来刻画位置关系，由位置关系来刻画数量关系进行应用。例2让学生再次体会集合思想，并为例3做了一个铺垫，降低难度。例3引导学生用集合的观点理解图形。此外，这里还渗透了一种常用的数学思想方法——交集法。所谓交集法，就是先由部分条件构成一个集合，然后再由剩余的条件构成另一个集合，两个集合的交集就是问题的解。

师：通过今天的学习，你对圆有哪些新的认识吗？（学生畅所欲言。）

师：我们不仅从运动的角度了解了圆，也从集合的角度认识了圆，更理解了点与圆的位置关系与数量关系之间的一种转化。

二、教后反思

1.数学概念注重生成与预设相结合。

数学概念是客观世界中数量关系和空间形式的本质属性在人脑中的反映，是学生数学学习的逻辑起点，是学生进行数学思维的核心，是数学思想与方法的载体，在数学学习过程中具有十分重要的意义。在揭示新知阶段，教师让学生经历了用圆规和绳子两种不同工具画圆的过程，感受圆是怎样产生的，使学生在动手操作的过程中理解什么是圆，从而抽象、归纳出圆的定义。在这节课中，教师对圆的定义的教学，是把已有的知识和经验作为新知识的生成点，当学生的尝试、探究有了生成时，教师不断引导，使得圆的概念在学生的概括中一步步完善，定义的给出合情合理，学生的抽象归纳显得水到渠成。

2.数形结合思想主要体现在点与圆的位置关系上。

平面上的一个点与圆存在3种关系：点在圆内、点在圆上、点在圆外，这3种关系可以直接判断。但通过学生的探索，发现点与圆的位置关系又和点到圆心的距离和圆的半径的大小比较上存在着等价的关系。前者是从图形的角度进行的研究，后者是从数量的角度进行的研究，一个是形，一个是数，两者很好地结合并相辅相成。转化思想是数形结合思想的延续，因为数形结合思想就是把图形问题转化成代数问题，把代数问题转化成图形问题。学生在运用数形结合思想的同时，也在运用着转化的思想。

3.例题的设计环环相扣，目的清晰。

设计的例题既加深了学生对集合概念的理解，又突出了点和圆的位置关系与点到圆心的距离和半径之间的数量关系之间的相互转化，为本章后续内容的教学做好了铺垫。同时习题的设计突出层次，不同的学生能获得不同的体验，此外解决问题的方法、蕴含的思维含量都具有挑战性，这样更有利于学生认识圆的本质及点与圆的位置关系，增强对数学的学习兴趣。重在理解教学内容，而不是停留在没有思维的运算和反复操练上。

（作者为江苏省丹阳市华南实验学校教师）