基于弹性抗力法的基坑支护结构三维变形分析

,

(天津大学 建筑工程学院，天津 300350)

基于弹性抗力法的基坑支护结构三维变形分析

王成华,李凯

(天津大学 建筑工程学院，天津 300350)

对比了目前已有的基坑支护结构内力及变形分析方法，提出了空间弹性抗力法的概念。对该方法的计算模型、原理及公式进行了简述，并编制了相应分析计算程序。结合基本算例，分析了不同支撑情况下支护结构的内力及变形情况，并总结出角部支撑的合理布置方式，同时分析了超载不均匀情况下支护结构的内力与变形情况，研究了平面小尺寸基坑是否需要布置支撑的问题，对基坑支护结构设计具有一定的参考价值。

支护结构；内力；变形；空间弹性抗力法

0 引言

目前，基坑工程的数量不断增多，其安全性与经济性也受到越来越多的重视。合理的基坑工程方案不仅能够保证基坑的安全，也能够减少经济的投入，达到安全经济的效果。因此，一个合理、有效的基坑设计方法就显得尤为重要。

基坑设计的重点在于支护结构的内力及变形分析，分析的结果越贴近实际，基坑设计方案也就越安全、越经济。早期的分析方法主要有静力平衡法、弹性抗力法和有限元法[1]。其中，静力平衡法适用于普通挡土墙及开挖深度不深的钢板桩；有限元法适用于各种基坑支护结构，且计算结果精确，但计算参数的选取较难，未能广泛应用；弹性抗力法计算简单，且能够编成程序计算，更加便捷，应用最为广泛。

1 现有的弹性抗力法

为了提高计算结果的精度，专家学者们对弹性抗力法进行了改进，并得到了不同的计算方法。目前的弹性抗力法主要包括以下几种：

1.1平面弹性抗力法

平面弹性抗力法，即早期弹性抗力法和后续改进后仍用于平面情况下的改进方法[1-3]。其基本假定为：(1)平面应变假定，忽略支护结构的空间作用；(2)土弹簧假定，开挖面以下墙体变形不能超出主(被)动极限位移，土抗力不能超出土体极限承载力。其中，土压力分布模式多采用矩形分布[1]。

平面弹性抗力法操作简单，易于编制程序，在早期得到广泛应用。但该法未能考虑支护结构与支撑体系、支护结构与土体的相互作用，导致其计算精度略低。随着计算精度要求的提高，平面方法的精度不再满足要求。

1.2拟三维弹性抗力法

经过相应改进，弹性抗力法能够初步做到空间情况下的内力与变形分析，即拟三维弹性抗力法[2,4]。

拟三维方法的基本原理是：分别考虑支护桩和支撑体系的变形与内力，支撑与支护桩联结点处只考虑水平力作用，忽略弯矩和扭矩，通过联结点处的位移协调方程，多次迭代，求得支护结构和支撑体系的位移和内力。

拟三维方法能够初步考虑支护结构与支撑体系、支护结构与土体的相互作用，所得结果较平面方法更准确。但结点处只考虑水平力作用，忽略弯矩和扭矩的作用，计算模型与实际受力情况不符，所得结果精度仍显不足。

1.3空间弹性抗力法

为了更好地考虑支护结构与支撑体系、支护结构与土体的相互作用，专家学者们将弹性抗力法与杆系有限元法结合，得到空间弹性抗力法，并在此基础上做了不同程度的修改[5-7]。

空间方法的基本原理是：将支护结构、支撑体系简化为空间杆系结构，支护结构上有土弹簧支座，且作用有来自土体的土压力，运用杆系有限元的方法进行计算，求得结构的内力与变形。

空间方法是弹性抗力法与有限元方法的有效结合，能够更好地考虑支护结构与支撑体系、支护结构与土体的相互作用，更能满足目前基坑支护结构变形分析的计算精度要求。

2 空间弹性抗力法分析模型

2.1支护结构

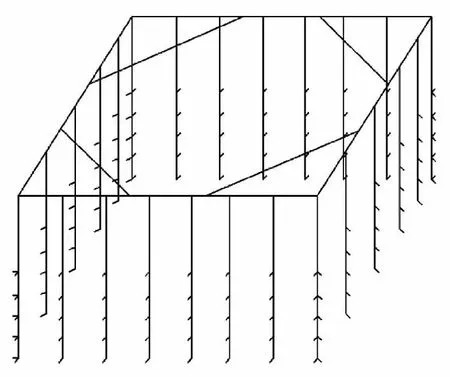
图1 空间弹性抗力法计算模型

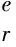
(1)

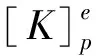
2.2支撑体系

支撑体系包括帽(腰)梁、支撑及立柱。立柱主要承受支撑体系的自重，而计算模型忽略了支撑体系的重力作用，故支撑体系只考虑帽(腰)梁和支撑。

在基坑支护结构设计中，帽(腰)梁对保证支护结构的稳定起着重要作用[5]，将其简化成空间梁单元可以充分考虑这种作用，使计算结果更准确。本文考虑桩与帽(腰)梁、内支撑与帽(腰)梁在结点处的连接方式为固接，即考虑弯矩、剪力和轴力作用，故支撑也采用空间梁单元模拟。

2.3土压力计算

采用经典土压力理论计算支护结构上作用的土压力，当桩后土体为黏性土时，土压力按照朗肯土压力理论计算，为无黏性土时则按照库伦土压力理论计算。

2.4考虑施工过程的有限元方程的修正

当基坑支护结构具有多道支撑时，需逐一进行施工。因此，当后续支撑施工完成并参与受力时，支护结构本身已具有一定程度的变形。在进行变形分析时，应该将这部分变形考虑进去，故修正后的有限元方程[6]如下

(2)

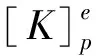
2.5程序编制

通过Fortran软件将本文所述空间弹性抗力法编制成程序，再对基坑支护结构进行三维变形分析。

图2 基本算例示意图

3 算例分析

3.1基本算例

建立基本算例如下：支护结构及相应土性指标如图2所示，基坑开挖深度为9 m，桩体嵌固深度为10 m；地下水位取至地面，采用朗肯土压力方法，按照水土分开计算土压力。支护桩体采用灌注桩，直径为800 mm、中心间距为1 000 mm。采用矩形基坑，平面尺寸为19 m×17 m，桩顶设有一道帽梁，截面尺寸为0.8 m×0.5 m，角部设有角撑，其截面尺寸为0.5 m×0.5 m。超载q1=q2=q3=q4=35.768 kN/m，灌注桩、帽梁和角撑均采用C25砼，剪切变形模量G取相应弹性模量E的40%[8]。

3.2角桩、中心桩的内力及位移分析

分别取长边AD与短边JA的中心桩体及A端点角桩的X、Y方向，给出相应的位移图与弯矩图，如图3，其中桩体位移以桩体向坑内方向为正，桩体弯矩以桩体基坑外一侧受到拉力为正。

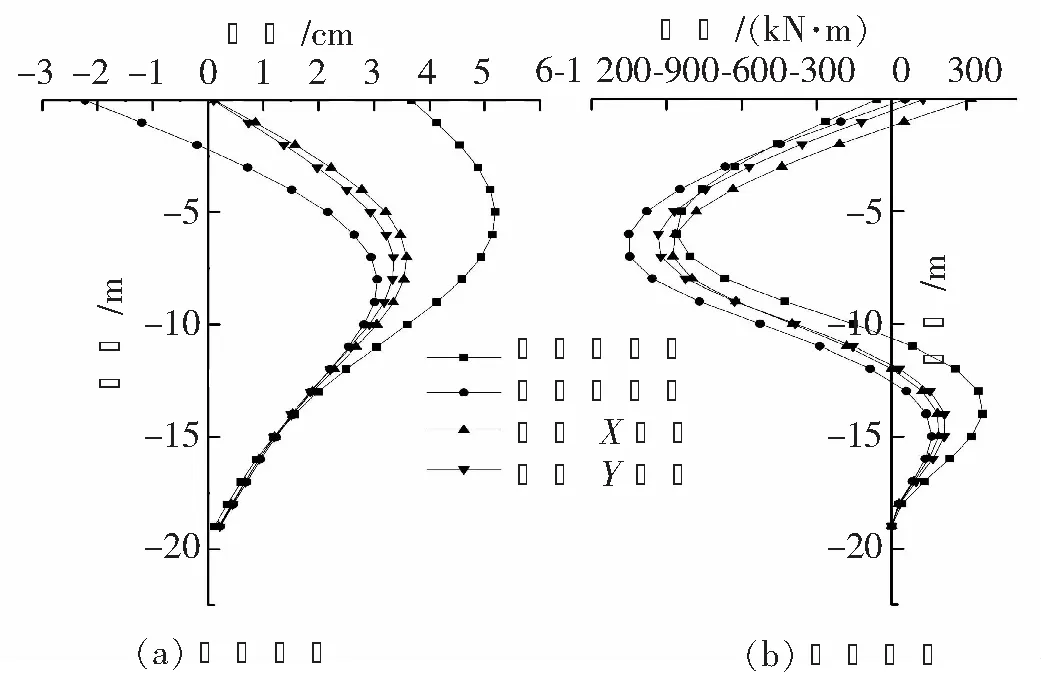
图3 不同位置桩的位移和弯矩

由图3(a)可以看出，支护桩体的最大位移出现在临近基坑底面的位置，且桩的顶部位移越小，桩体最大位移的位置越靠近基坑底面；基坑长边中心桩的最大位移值最大，超出其他桩体最大位移50%以上，在支护桩体变形控制中应予以重点关注。

由图3(b)可以看出，基坑长边中心桩的弯矩值分布最均匀，但短边中心桩的最大弯矩值最大，且超出其他桩体最大弯矩值10%～30%,故内力分析应重点考虑短边中心桩的最大弯矩值。

图4 支撑平面布置(单位：m)

3.3角部支撑布置的优化

算例中，帽梁及支撑采用混凝土，故帽梁上支撑点的间距不宜大于 9 m，角部撑的长度不宜大于9 m，与帽梁之间的夹角宜取45°～60°[9]。在上述原则的基础上，通过改变帽梁长边和短边上的支撑点位置，得到不同的支撑布置方式，见图4。

采用空间弹性抗力法进行计算，得到支护结构各部分的内力值和位移值，取支撑体系帽梁段BC、CD、DE、EF4段的正、负弯矩的最大值及端点C、D、E、F4点的弯矩值，绘制成表，见表1。帽梁其余部分及端点的相应弯矩由对称性可得。其中，帽梁弯矩以帽梁基坑内一侧受到拉力为正。

表1 不同支撑形式下帽梁各部分最大弯矩及各端点弯矩 kN·m

注： “-”表示该帽梁部分不存在相应弯矩。

由表1可以看出，支撑方式一、三、四下帽梁所受正弯矩最大值均出现在BC段，而支撑方式二下正弯矩最大值出现在CD段，且支撑二下帽梁所受正弯矩最大值最小，支撑一次之；帽梁上各端点弯矩皆为负值。帽梁所受最大负弯矩都发生在支撑点处，其中，支撑方式一、二、三下最大负弯矩出现在支撑点E，支撑方式四下为支撑点C，且支撑一下帽梁所受最大负弯矩最小，支撑二次之。以帽梁正、负弯矩最大值的比值作为弯矩分布均匀的标准，即比值越接近1，弯矩分布越均匀。经计算，4种支撑方式下的比值分别为0.873、0.791、1.059、1.121，则支撑一下帽梁的最大正、负弯矩均较小，且分布均匀。

为方便观察，将帽梁变形计算结果放大50倍，得到如图5所示的变形图。

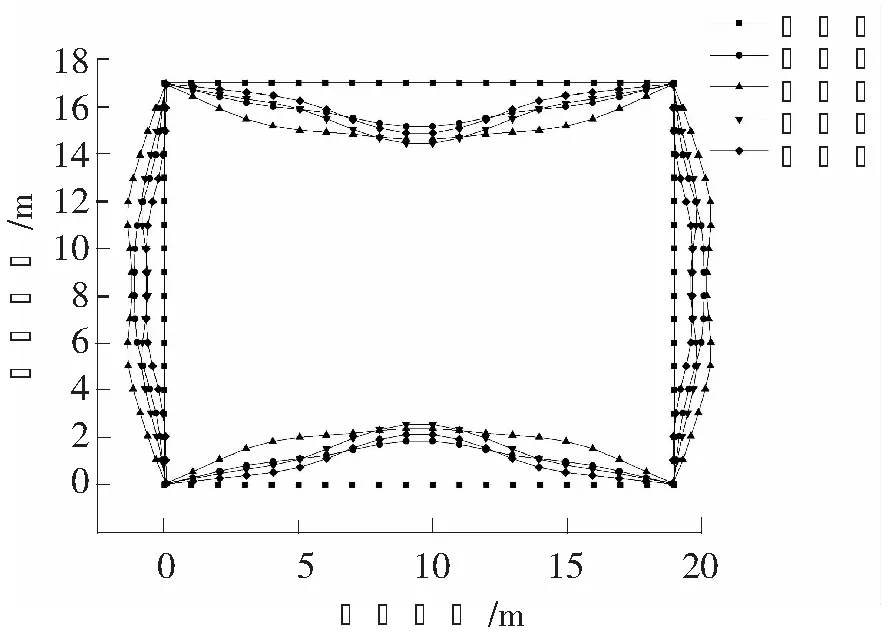
图5 不同支撑形式下帽梁变形图

通过对比图5中变形曲线可得结论如下：(1)BC段越短，其变形趋势越平缓，此时，控制长边位移值的重点在于降低B、C端点处的位移值；(2)长边受到的一部分土压力会通过角部支撑传给短边，使短边的一部分产生反方向的位移，短边的位移值减小；(3)相同条件下，CD段越长，E端点处的负向位移值越大，同理，DE段越长，C端点处的正向位移值越小；(4)对于帽梁各边，中间部分长度小于或略大于两端部分长度时，该边的变形曲线较平缓，能够更好地发挥该边各部分的性能。

将长边AD与短边JA的中心桩及A端点角桩的X、Y方向分别命名为桩体1～桩体4，并列出不同支撑形式下不同位置桩的最大位移及最大弯矩，见表2、表3。

表2 不同支撑形式下不同位置桩的最大位移 cm

注： “—”表示不存在相应位移。

表3 不同支撑形式下不同位置桩的最大弯矩 kN·m

由表2可知：(1)4种支撑情况下，只有桩体2存在负位移，这是由于支撑使桩体顶部产生负向位移，详情可参照帽梁变形；(2)不同支撑形式下，不同桩体的正位移最大值变化不超过10%，而桩体2的负位移最大值变化最多可达到50%以上，即支撑方式对短边中心桩的顶部负向位移影响较大，而对所有桩体正位移最大值的影响很小；(3)不同支撑形式下，桩体1的正位移最大值总是最大，即支撑方式对最大桩体位移的发生位置无影响。

由表3可知，不同支撑形式下，桩体最大弯矩均出现在桩体2上，且最大弯矩值相差不超过3%，故支撑方式对桩体最大弯矩出现位置无影响，对其值影响亦不大。

在相同条件下，按照支撑方式一布置角撑，帽梁的变形小，且各部分及端点的弯矩分布均匀，同时桩体位移最大值最小，弯矩最大值较小，为理想的支撑布置方式。支撑方式一下不同位置桩的位移及弯矩见图3。

3.4超载不均布的内力及位移分析

实际工程中经常出现基坑某一边或几边堆放重物而导致基坑超载不均布的情况，此时，基坑支护结构各边受力情况发生改变，其内力值与位移值也出现变化。

如图3，在基本算例的基础上，改变超载q1的大小，造成基坑超载不均布的情况，通过计算得到帽梁和支护桩体的内力值和位移值。为便于观察基坑整体的受力及变形情况，将帽梁AD边和GJ边的正弯矩、负弯矩、正位移及负位移的最大值绘制成表，见表4。

表4 不同超载下帽梁AD边和GJ边的最大弯矩和位移

注：表中q1单位为kN/m；弯矩单位为kN·m；位移单位为cm；“—”表示该帽梁部分不存在相应值。

随着AD边超载q1的增大，基坑整体向GJ边偏移，则AD边各点位移均为正，故表3中AD边只取其正位移最大值。由表4可以看出，随着超载q1的增大，AD边和GJ边的弯矩始终保持对称，AD边的正弯矩最大值逐渐增大，负弯矩最大值逐渐减小，GJ边亦然。

取帽梁的最大弯矩值和位移值及各自位置，绘制成表5。由表5可以看出：随超载q1的增加，帽梁弯矩最大值增加，位置不变，即帽梁短边的支撑点处；帽梁最大位移总是发生在长边跨中位置，且随q1的增加而增大。

表5 不同超载下帽梁的最大弯矩和位移及相应位置

注：表中最大弯矩取绝对值。

将基坑边AD、GJ、JA的中心桩及A、J端点角桩的X、Y方向分别命名为桩体1-7，并列出不同超载下不同位置桩的最大位移及最大正、负弯矩，见表6～表8。

表6 不同超载下不同位置桩的最大位移

注：表中q1单位为kN/m；位移单位为cm。

由表6可以看出，随着超载q1的增大，桩2、3、7的最大位移逐渐减小，桩1、4、5、6的最大位移逐渐增大，其中桩3和桩7的最大位移变为负向并增大，桩4和桩6最大位移保持一致，桩1最大位移值最大，故桩体位移分析应重点关注基坑超载一侧的中心桩体。

表7 不同超载下不同位置桩的最大正弯矩

注：表中q1单位为kN/m；弯矩单位为kN·m。

表8 不同超载下不同位置桩的最大负弯矩

注：表中q1单位为kN/m；弯矩单位为kN·m。

图6 基坑平面图(单位：m)

结合表7、表8可知，随着q1的增加，桩1的正弯矩最大值超过负弯矩最大值，其余桩体皆以最大负弯矩为最大弯矩值；对于不同超载下不同位置的桩，桩3和桩7的最大弯矩值最大，故桩体内力分析应重点考虑基坑超载一侧对面的角桩及短边的中心桩。

3.5平面小尺寸基坑的内力及变形分析

在基本算例的基础上，其余参数保持不变，只修改基坑支护结构平面尺寸，如图6为小平面尺寸的基坑。

在本例中，需要分别计算帽梁不加支撑和加支撑情况下的内力值和变形值，支撑布置情况如图6。为便于观察帽梁变形情况，将计算结果放大30倍，如图7所示。两种情况下帽梁的位移值和挠度限值[8]见表9所示。

表9 有无支撑帽梁的最大位移和挠度限值 cm

如图7，在相同的条件下，角部支撑的存在使帽梁的位移减小许多，角部支撑可以使长度、宽度两个方向的土压力互相传递，相互抵消，达到减小帽梁变形的效果；相同条件下，无论角部支撑是否存在，帽梁的最大位移都出现在跨中，即基坑各边中间处的支护桩体变形最大，这是基坑的对称性导致的。

按照文献[9]的规定，帽梁边长为11 m，大于9 m，宜设置角撑，使支撑点间距小于9 m。然而，由表10可以看出，加支撑的情况下帽梁最大位移是挠度限值的1/5，安全储备过高，而不加支撑情况下帽梁的最大位移接近其挠度限值，充分发挥了帽梁的变形作用，经济性好。

有无支撑两种情况下基坑中心桩的位移和弯矩，见图8。

由图8可以看出：(1)无支撑时，中心桩体的最大位移超出有支撑的情况27%，为5.19 cm，空间弹性抗力法假定桩体为受弯梁，依据《混凝土结构设计规范》[8]算得桩体的挠度限值为6.33 cm，故无支撑情况下桩体的最大位移依旧能够满足要求挠度；(2)有支撑时，桩体所受弯矩最大值略大，仅超出无支撑情况10%，但无支撑情况下，桩体所受弯矩分布更均匀。因此，本例中按照无支撑情况进行支护结构设计更合理。

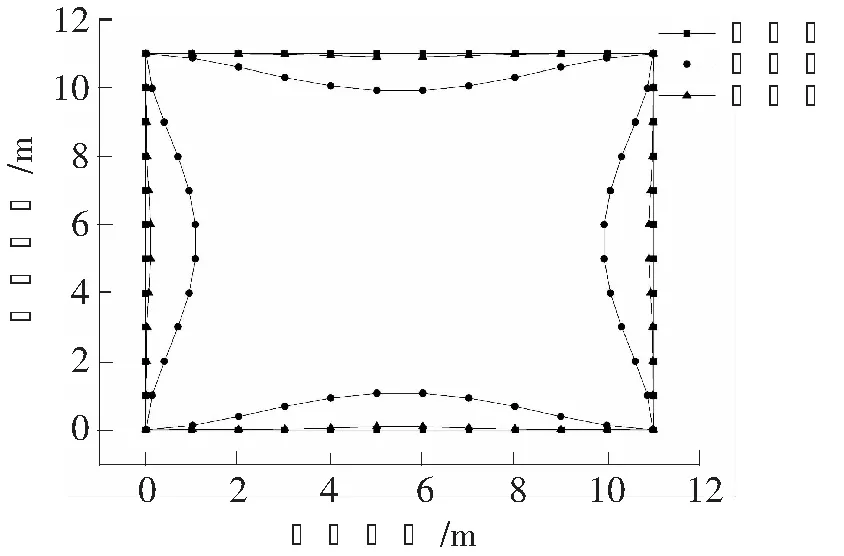
图7 有无支撑情况下帽梁变形图

图8 有无支撑情况中心桩的位移和弯矩

4 结论与建议

本文介绍了空间弹性抗力法的基本原理，并运用该方法研究了矩形基坑排桩支护结构的内力与变形规律。得到初步结论与建议如下：

(1)对于支护结构，支撑能够传递支护结构不同边上受到的土压力，显著减小支护体系的变形，使支护结构的整体空间效应得到更好的利用。建议在基坑平面较大或开挖深度较深的情况下，设置支撑。布置角部支撑时应尽量使中间部分小于或略大于边跨部分，同时短边的边跨部分尽量加长，以接近或略高于长边边跨长度为宜。

(2)由于堆放重物或其他原因造成的基坑各边超载不均布情况，超载数值大的基坑边变形大，应采取相应措施，如增大桩径或减小桩间距，同时可减小相反基坑边的支护桩桩径或加大该边的桩间距。

(3)在实际工程中，经常会遇到这样一类基坑，其平面尺寸较小，存在长度略大于9 m的一边或多边。此时，不应盲目添加支撑，应对其进行内力与变形分析，在不超过挠度限值的情况下可以不添加支撑，从而达到安全、经济的目的。

(4)本程序能够对基坑支护结构进行整体分析，同时考虑了施工过程的影响，所得结构较准确。但土压力计算模式采用平面方法，且未能考虑土体位移与土压力的关系，程序仍有待进一步完善。

[1]秦四清. 基坑支护设计的弹性抗力法[J]. 工程地质学报, 2000,8(4): 481-487.

[2]王岩. 弹性抗力法在深基坑支护结构计算与分析中的应用[D]. 天津：天津大学, 1995.

[3]杨光华. 深基坑支护结构的实用计算方法及其应用[J]. 岩土力学, 2004, 25(12): 1885-1896+1902.

[4]陆培毅, 刘 畅, 顾晓鲁. 深基坑支护结构支撑系统简化空间分析方法的研究[J]. 岩土工程学报, 2002, 24(4): 471-474.

[5]陈晓平, 闫 军. 深基坑支护结构的三维杆系有限元分析[J]. 岩土力学, 2001, 22(3): 258-261.

[6]潘 泓, 曾律弦. 深基坑环梁支护结构空间分析方法的研究[J]. 岩土工程学报, 2005, 27(7): 849-852.

[7]陈 伟, 吴才德, 黄吉峰, 等. 深基坑支护结构的三维分析原理、应用及验证[J]. 岩土工程学报, 2007, 29(5): 729-735.

[8]中国建筑科学研究院. GB 50010-2010 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2010.

[9]中国建筑科学研究院. JGJ 120-2012 建筑基坑支护技术规程[S]. 北京: 中国建筑工业出版社, 2012.

3DDeformationAnalysisofRetainingStructuresofFoundationPitsBasedonElasticResistanceMethod

WangChenghua,LiKai

(School of Civil Engineering, Tianjin University, Tianjin 300350, China)

Methods to analyze the existing internal force and deformation of foundation pits' retaining structures are compared, and the concept of space elastic resistance method is put forward, including its calculation model, principle, formulas and corresponding program. Through an example, the reasonable arrangement for corner supports is summarized by analyzing the internal force and deformation of retaining structures under different supports, and the inner force and deformation of the supporting structure under inhomogeneous overload are analyzed. Moreover, the question whether the supports need to be laid to the foundation pits with small plane size is investigated. These conclusions are of certain reference value for the design of foundation pits' retaining structures.

retaining structures;internal force;deformation;space elastic resistance method

TU46+3

： A

： 2095-0373(2017)03-0012-08

2016-06-15责任编辑:刘宪福

10.13319/j.cnki.sjztddxxbzrb.2017.03.03

国家自然科学基金(51478313)

王成华(1959- )，男，博士，教授，主要从事岩土工程、地下工程等领域的教学与科研工作。E-mail: chwang@tju.edu.cn 王成华,李凯.基于弹性抗力法的基坑支护结构三维变形分析[J].石家庄铁道大学学报:自然科学版,2017,30(3):12-19.