基于改进蚁群算法的装配线VRPTD问题研究

, , ,

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

基于改进蚁群算法的装配线VRPTD问题研究

刘凯,牛江川,申永军,韩彦军

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

采用改进蚁群算法求解了装配线物料配送的VRPTD问题(带最后期限时间窗的车辆路径问题)。通过信息素动态更新设计，使改进蚁群算法具有自适应性，克服了传统蚁群算法在遍历寻优过程中容易出现停滞和陷入局部最优解的缺点。通过进一步对启发函数可见度进行改进设计，提高了算法的全局搜索能力。仿真结果表明，改进蚁群算法可以很好地求解装配线VRPTD问题，这对实际应用有一定的参考价值。

改进蚁群算法；装配线物料配送；带最后期限时间窗的车辆路径问题

0 引言

在准时化生产模式下，需要对装配线上的各类物料实施多品种、小批量的准时配送。在正确的时间，将正确的物料配送至正确的工位是保证装配线顺利进行的关键[1]。

针对物流配送车辆路径问题(VRP)，许多学者根据实际情况提出了解决方案：杨斯淇[2]针对生产车间VRP问题，建立了牵引车配送路线问题的数学模型，结合使用遗传算法和插入法，对传统的遗传算法做了改进，简化了求解过程；任星球[1]建立了带缓存区配送方式下的牵引车配送路径模型，设计混合量子进化算法解决装配线VRP问题。针对装配线物料配送带最后期限时间窗的车辆路径问题(VRPTD)的研究，徐智慧等人[3]建立了基于灾后物资供应的VRPTD模型，采用遗传算法求解，对应急物资的调度有指导意义；赵思敏[4]考虑粮食应急物流道路阻塞与时间的相关函数，建立以满意度最大为目标的VRPTD模型，通过遗传算法与蚁群算法的演示程序将两个算法进行对比，结果表明相同的前提条件下，蚁群算法在求解速度、最优解质量和算法稳定性等方面优于遗传算法。吴隽等[5]针对物流配送中的带时间窗的车辆路径问题(VRPTW)，提出了一种改进的最大最小蚁群算法，引入了局部搜索策略二次优化(2-opt)，算法寻优过程得到了优化；Du et al[6]提出了贪婪策略与蚁群算法相结合的自适应蚁群算法，效果优于传统的自适应蚁群算法。

本文采用改进蚁群算法对装配线VRPTD问题进行了优化研究，通过信息素动态更新、启发函数ηij的改进设计，使算法具有自适应性，在一定程度上克服了传统蚁群算法在遍历寻优过程中容易出现停滞和陷入局部最优解的缺点。

1 牵引车物料配送的VRPTD数学模型

已知缓存区、工位和道路条件，在每个工位段需求和服务时间窗已知的条件下，对m辆额定载重量为Q(单位kg)的运输车辆，n个工位，确定运输车辆的最佳配送路线。设n个工位集合V={v1,v2,…,vn}，V中两个工位集合D={Dij|vi，vj∈V}，工位i、j坐标分别为(xi,yi)、(xj,yj)，两工位间距离为

(1)

模型满足以下约束条件：

(1) 物料配送不考虑车间内通行路线的限制，各个工位间的距离为理想的直线距离。

(2) 每个工位的需求量均不超过运输车辆的额定载重量，即max(qi)≤Q，其中第i个工位的需求量为qi(i=1,…,n)，qi的单位为kg。

(3) 每一个工位所需的物料只能由一台车配送完成，每辆车可以配送多个工位，且所有车辆配送路线均起止于缓存区。

(4) 每个工位都有最后服务期限的时间窗[0,bi]，物料配送必须在此时间窗内完成，否则将受到惩罚。

在建立数学模型之前，需要确定缓存区使用车辆数，使用文献[1]中的公式来确定需要的车辆数m

(2)

式中，qi(i=1,…,n)为第i个工位的需求量；Q为车辆的额定载重量；a取0.85，约束条件越多，车辆装卸物料越复杂，a值越小[7]。

引入0-1变量，yik表示工位i所需要的物料由运输车k配送。当工位i由运输车k配送时yik=1，否则yik=0。

在满足上述约束条件下，确定运输车辆的最佳配送路线，使总行驶距离最小，确定总行驶距离为目标函数f，数学模型如下

(3)

式中，当运输车k从i行驶到j时xijk=1，否则为0。并满足以下约束条件

(4)

式中，下标0表示缓存区，式(4)保证了有m辆运输车从缓存区出发，进行物料配送。

(5)

式(5)保证了每一个工位都有一辆车负责物料配送。

(6)

(7)

式(6)、式(7)保证每个工位只有一辆车执行物料配送任务。

(8)

式中，Q为每辆车的额定载重量。车辆的运送总质量应不超过车辆的最大载重，式(8)保证每条路径上车辆的装载量约束。

(9)

式中，p为n个工位中任意一个工位，式(9)保证每辆车到达某工位后仍从该工位离开。

(10)

式中，sik为运输车k在sik时刻配送物料至工位i，sik∈[0,bi]；K为很大的正数。式(10)保证车辆不早于sik+tij到达工位j。

(11)

式中，u为运输车的恒定速度；tij为运输车从工位i到工位j的行驶时间。

2 VRPTD问题蚁群算法的设计与改进

2.1蚁群算法设计

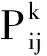
(12)

式中，信息启发因子α和期望启发因子β分别表示信息素和期望值的相对重要程度，α值越大，表示信息素浓度在状态转移中起的作用越大，同样β值越大，表示启发函数在状态转移中起的作用越大，即蚂蚁会以较大的概率转移到距离较短的工位。

(13)

式中，allowedk为蚂蚁k下一步能选择的工位集合；V={v1,v2,…,vn}为工位集合。开始时，allowedk中有(n-1)个元素，随着迭代次数的增加，allowedk中的元素逐渐减少，直至为空，即表示此时蚂蚁已遍历完集合中所有工位。禁忌表Tabuk存储并记录蚂蚁k走过的工位。

(14)

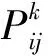
蚂蚁每完成一次循环，需要考虑信息素的挥发，蚂蚁在释放信息素的同时，各个工位路径上的信息素也在逐渐消失，需要实时更新各个工位路径上的信息素[10]。

(15)

2.2算法改进

2.2.1 信息素动态更新改进

蚁群算法中信息素挥发系数的大小直接关系到蚁群算法的全局搜索能力和收敛速度[11]。当问题规模较大时，由于信息素挥发系数的存在，从未被搜索到的路径上的信息素浓度会逐渐减小到接近于0。当信息素挥发系数过小时，路径上的信息素浓度增大会使以前搜索过的路径再次被选择的可能性增大，从而降低了算法的全局搜索能力，增大信息素挥发系数虽然可以提高算法的全局搜索能力，但又会使算法的搜索速度降低[8]。因此，通过改变信息素挥发系数，提出了一种信息素挥发系数自适应变化的蚁群算法，希望通过自适应的改变信息素挥发系数提高算法的全局搜索能力。

当求得的最优解在连续若干代内没有明显改进时，按式(16)对信息素挥发系数进行更新。

(16)

式中，信息素挥发系数ρ应在初始给定最大值和最小值之间取值；参数0.95是信息素挥发系数更新系数，每次下降5%，直到小于信息素挥发系数的最小值ρmin，ρmin可以防止因信息素挥发系数过小而降低算法的收敛速度。

本算法与基本蚁群算法相比取消了信息素的局部更新即二次优化2-opt操作，而是进行信息素的全局更新以此来提高算法的收敛速度。

2.2.2 启发函数的改进

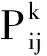
(17)

改进后的可见度，有助于提高算法解决带最后期限时间窗的车辆路径问题的全局性。

2.3算法实现流程

基于上述设计，改进后的蚁群算法求解VRPTD问题步骤如下，其算法流程如图1所示。

图1 改进蚁群算法流程图

(1) 初始化参数。开始计算之前，需要对相关参数进行初始化，如蚂蚁数目n、车辆数目m、重要度系数α、能见度系数β、权重系数γ、挥发系数ρ、最小挥发系数ρmin、最大迭代次数NC_max、车辆载重量Q、车辆装载量load_w等。

(2) 构建解空间。将未服务的工位放入V={v1,v2,…,vn}中，对于蚂蚁k(k=1,…,n)按照公式(12)计算下一个要服务的工位，直到所有蚂蚁访问完所有工位。

(3) 容量和时间判断。设置蚂蚁的禁忌表索引号k=1，每服务一个工位，判断容量和时间是否符合要求，符合则将服务过的工位置于当前tabu(k)中，不符合则跳转到第2步。

(4) 更新信息素。计算各个蚂蚁走过的路径长度，计算当前迭代次数中的最短路径。同时根据公式(15)、公式(16)、公式(16)对各个工位路径上的信息素进行更新。

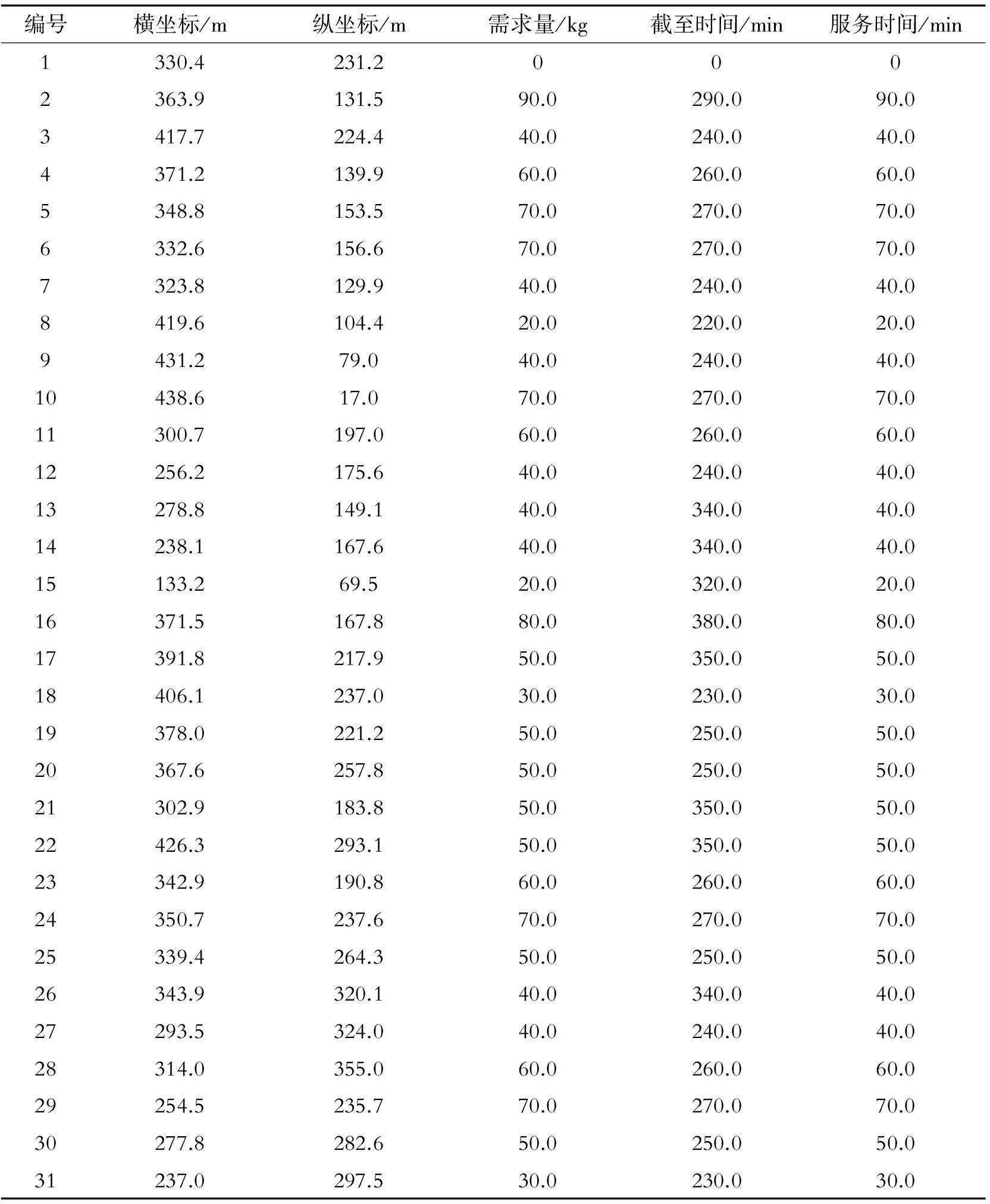
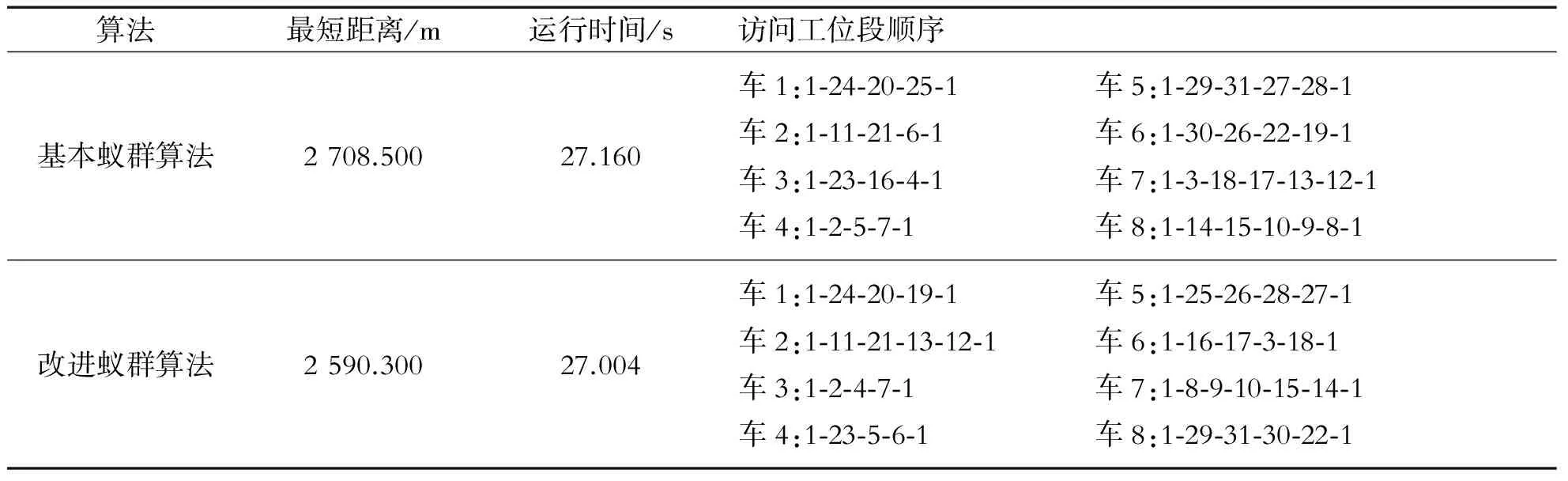
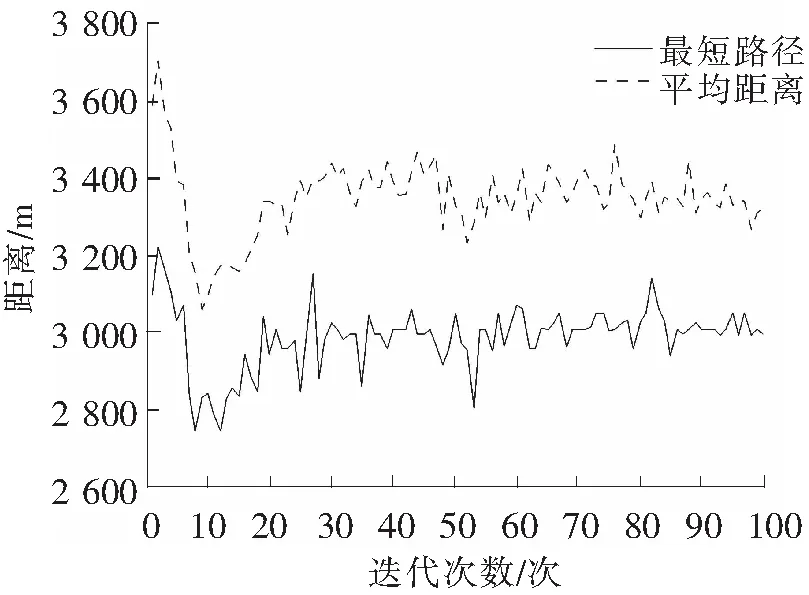
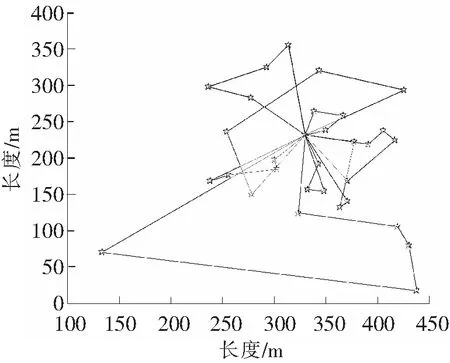
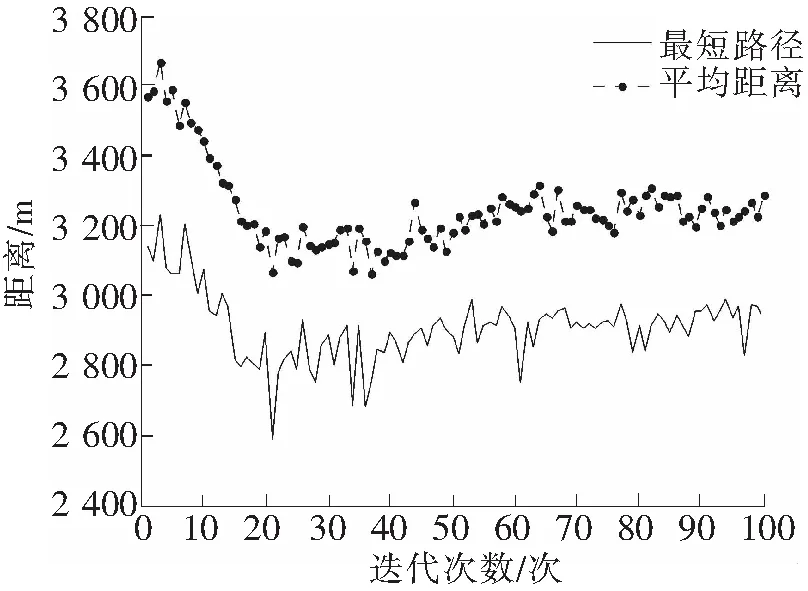
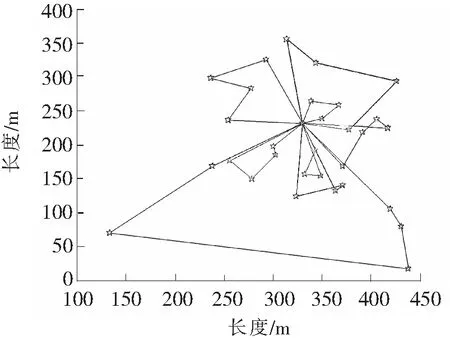
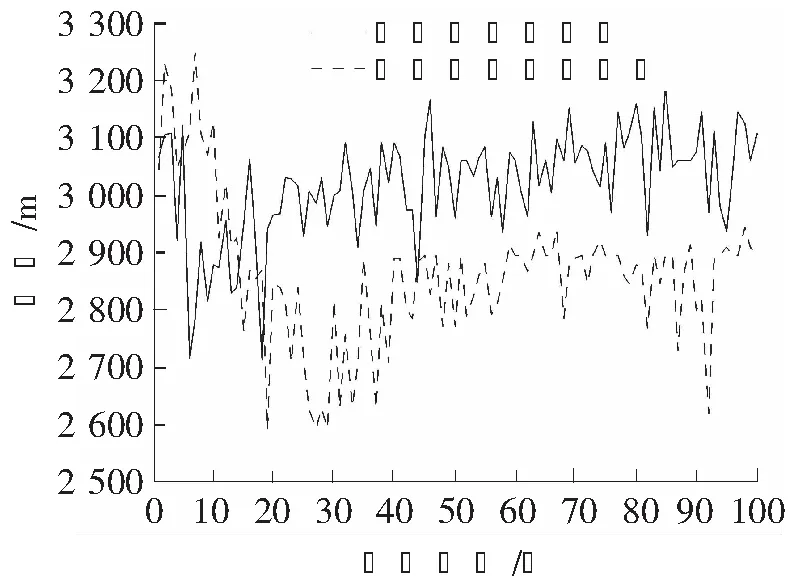
(5) 判断终止条件。当迭代计数器NC

3 算法测试及结果分析

3.1算法测试

为了测试改进后的蚁群算法求解VRPTD问题的效果，分别用基本蚁群算法和改进后的蚁群算法求解25个客户点的Solomon基准实例[12]。Solomon例库有C型、R型、RC型3种，它们之间的区别在于客户点坐标的设置方式和时间窗的设置不同。C型例库按照结构性方式来设置客户坐标，R型例库则是以均匀分布的方式来设置客户坐标，而RC型例库则是按以上两种例库混合的方式来设置客户坐标[13-14]。

采用Matlab对改进蚁群算法进行测试，各个参数设置如下：蚂蚁数目n=25，车辆数目m依具体情况而定，实例C101、R101、RC101分别对应的车辆数目为3、2、15，重要度系数α=3，能见度系数β=2，权重系数γ=2，挥发系数ρ=0.5，最小挥发系数ρmin=0.05，最大迭代次数NC_max=100，车辆载重量Q=200，车辆装载量load_w=0。测试结果如表1所示。

表1 Solomon C型、R型、RC数据集测试结果对比

3.2算例实现

由于Solomon测试例库中，C型数据集、R型数据集、RC型数据集每个工位处的服务时间分别为90、10、10，不是随机变化的。故采用如下算例，进一步对改进算法的有效性进行验证。具体算例数据如表2所示。

表2 某装配线工位点数据

蚂蚁数目n=31，车辆数目m=9，算法其它初始设置与上例相同。经过仿真分析，分析结果如表3所示。

表3 算例仿真结果对比

采用基本蚁群算法，迭代过程中最短距离、平均距离变化和路径规划结果，如图2和图3所示。

图2 基本蚁群算法最短距离、平均距离变化

图3 基本蚁群算法路径规划结果

由图2可以看出，传统的蚁群算法求解VRPTD问题时，最终求得的最短距离在2 700 m左右，在第10次迭代的时候，找到了最优解，求解效率较高。由图3可以看出，基本蚁群算法求得的路径规划结果有重复的路径出现，求解结果还有优化的空间。

采用改进蚁群算法，迭代过程中最短距离、平均距离变化和路径规划结果，如图4和图5所示。

图4 改进蚁群算法最短距离、平均距离变化

图5 改进蚁群算法路径规划结果

由图4可以看出，改进后的蚁群算法求得的最短距离在2 600 m左右，缩短了近100 m，第20次迭代的时候找到了最优解，寻优效率没有改进前高，但寻优结果较改进前好。由图5可以看出，改进后蚁群算法求得的路径规划结果避免了重复路径的出现，进一步优化了求解结果。

算法改进前后最短路径对比，如图6所示。

图6 最短路径前后对比

由图6知，改进后的蚁群算法求解结果优于基本蚁群算法求解结果。迭代初期，改进后的蚁群算法寻优效率并没有传统蚁群算法高，但是随着迭代次数的增加，改进后的蚁群算法由于对当前最优路径上信息素的充分利用，扩大了解的搜索空间，提高了算法的全局遍历性，并没有陷入局部最优解的死循环。

4 结论

通过对传统蚁群算法信息素更新和可见度设计方面进行改进，求解装配线物料配送优化问题。并通过实例对算法改进前后进行了对比分析，分析结果表明，改进后的蚁群算法在求解装配线VRPTD问题时不仅对解决蚁群算法的停滞问题非常有效，而且提高了运算精度，增大了收敛到全局最优解的可能性,有效地解决搜索停滞、早熟问题，对生产实际有一定的指导意义。

[1]任星球.制造企业装配线物料准时配送优化研究[D].杭州:浙江工业大学,2011.

[2]杨斯淇.基于遗传算法的制造企业生产物流牵引车配送路线优化研究[D].长春:吉林大学,2008.

[3]Zhihui X, Zhongning F. Study on emergency response of vehicle routing based on multi-commodity dispatch VRPTD model[C]//Transportation, Mechanical, and Electrical Engineering (TMEE),2011 International Conference on. IEEE,2011: 568-571.

[4]赵思敏.粮食应急物流系统的网络构建及路径优化[D].武汉:武汉理工大学,2011.

[5]吴隽,陈定方,李文锋,等.基于改进蚁群算法的有时间窗车辆路径优化[J].湖北工业大学学报,2008(3):9-12.

[6]Du D P, Zu Y R. Ubiquitous Computing Application and Wireless Sensor [M]. Berlin : Springer Netherlands,2015:663-670.

[7]邢文训,谢金星.现代优化计算方法[M].北京:清华大学出版社,1999.

[8]石华瑀.改进的蚁群算法在实际VRP中的应用研究[D].济南:山东大学,2012:33-34.

[9]Yi Y, Lin X, Sheng K, et al. Intelligent computing theories and methodologies[C].Berlin:[s.n.],2015:11-22.

[10]段海滨.蚁群算法原理及应用[M].北京:科学出版社,2005.

[11]吴小菁.基于挥发系数的自适应蚁群算法[J].福建金融管理干部学院学报,2010,1(1):54-58.

[12]Solomon Marius M. Algorithms for the vehicle routing and scheduling problem with time window con straints[J]. Operations Research,1987,35(2):254-265.

[13]Abdulkader M M S, Gajpal Y, Elmekkawy T Y. Hybridized ant colony algorithm for the multi compartment vehicle routing problem[J]. Applied Soft Computing, 2015, 37:196-203.

[14]刘凯,牛江川,申永军,等.基于遗传粒子群算法的堆垛机作业路径优化[J].石家庄铁道大学学报:自然科学版,2016,29(2):67-71.

StudyofAssemblyLineVRPTDProblemBasedonImprovedAntColonyAlgorithm

LiuKai,NiuJiangchuan,ShenYongjun,HanYanjun

(School of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

The distribution of materials for VRPTD(assembly lines with the deadline time windows vehicle routing problem) is studied by improved ant colony algorithm. By pheromone dynamically updated design, the improved ant algorithm is adaptive, which overcomes the shortcomings of the traditional ant colony optimization algorithm that traversal process is prone to stagnation and falling into local optima. The design of the heuristic function of the visibility, which based on further improvement, had improved the global search capability. The simulation results show that the algorithm can solve the problem of assembly line VRPTD, which has a certain reference value for practical application.

improved ant colony algorithm;assembly line material feeding;VRPTD

TH165.1

： A

： 2095-0373(2017)03-0055-07

2017-03-26责任编辑:车轩玉

10.13319/j.cnki.sjztddxxbzrb.2017.03.11

河北省自然科学基金(F2013210109)；河北省高等学校创新团队领军人才培育计划(LJRC018)；河北省教育厅自然科学青年基金 (QN2014151)

刘凯(1988-),男，硕士研究生,主要从事企业信息化与协调管理技术的研究。E-mail: lk1256229856@126.com 刘 凯,牛江川, 申永军,等.基于改进蚁群算法的装配线VRPTD问题研究[J].石家庄铁道大学学报:自然科学版,2017,30(3):55-61.