组合交路条件下城市轨道交通列车停站方案优化研究

(成都市规划设计研究院，四川 成都 610031)

组合交路条件下城市轨道交通列车停站方案优化研究

张要

(成都市规划设计研究院，四川 成都 610031)

目前国内城市轨道交通线网不断完善，线网密度提高，线路长度增长，大量超长线路的规划建设使得线路呈现客流时空分布复杂，平均运距增长的特征，这就要求运输企业制订更加合理高效的列车停站方案。以城市轨道交通超长线采取长大交路与分段衔接组合交路下的快慢车的停站方案为研究对象，充分考虑超长线的客流特征和行车组织基本要素，构建了基于乘客出行时间最小和轨道交通企业运输成本最小的多目标0-1规划模型，并设计合适的启发式算法对模型进行求解。

超长线;快慢车;停站方案;遗传算法

0 引言

截止2014年末，我国已有北京、上海等22个城市相继开通了80余条，共计2 500余km的城市轨道交通线路，其中超长线路(线路长度大于30 km)总里程为1 333 km，占到所有线路的34%。未来一段时间内，我国城市轨道交通仍将进行大规模的规划与建设。在各大城市城市轨道交通长远期规划当中，30 km以上、甚至50 km以上的超长轨道交通线路将成为网络中的重要组成部分，这部分线路的客流时空分布、平均运距等特征会与常规线路的客流特征存在较大的不同。时间分布上，超长线由于线路极长，其客流时间分布特征通常是常规线路5种客流形态(单向峰形、双向峰形、全峰形、突峰形和无峰形)的叠加和组合形式，导致超长线上的车站客流时间分布特征被弱化而变得无规则，如图1所示，此时若制定单一的符合线路客流时间分布特征的开行方案变得十分困难，无法满足乘客的出行需求和运输企业的利益；空间分布上，超长线的分布特征同样是各类常规形态的组合，如图2所示。

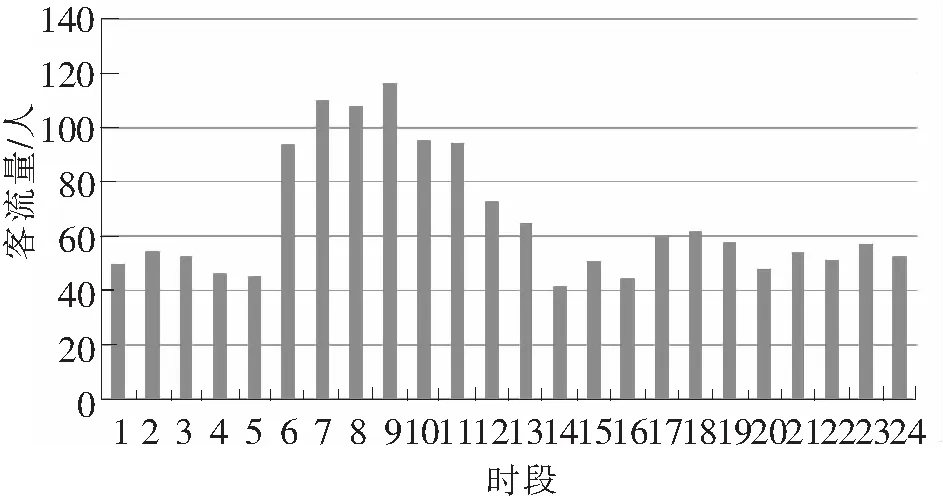
图1 单峰客流分布形态叠加相邻车站影响后的无规则形态

图2 凹陷型、凸起型和不规则型组合而成的客流断面分布特征

因此若在单一交路内实行较大的开行密度，将对运力造成严重的浪费，若开行密度过小，则不能满足乘客出行需求。国内外学者主要针对常规线路行车组织特征[1-3]超长线的行车组织特征[4-6]、单一交路快慢车[7-15]做了大量研究，鉴于超长线时空分布的复杂性，采用灵活多变的组合交路制定列车开行方案具有较大优势，针对长大交路和分段衔接交路的组合交路条件研究城市轨道交通列车的停站方案。

1 乘客选择行为分析

1.1基本假设和变量定义

(1)超长线上仅开行a,b,c3种列车，a为在第1个分段交路上运行的站站停列车，b为在第2个分段交路上运行的站站停列车，c为在长大交路上运行的跨站停快车，仅在少数客流量大，平均运距远的车站停车。

(2)3类列车采用相同车辆，技术参数相同。

(3)乘客到达车站的时间符合平均分布。

(4)乘客均可乘坐符合条件的列车乘车离站(不存在突发大客流)。

1.2参数及变量定义

1.3乘客选择行为分析

在组合交路快慢车开行方案下(如图3)，乘客可分为若干类，其出行选择行为如下：

(1)乘客的起终点站均为AB类车站(快车停车车站)时，乘客根据出行时间选择只乘坐快车或只乘坐慢车出行。

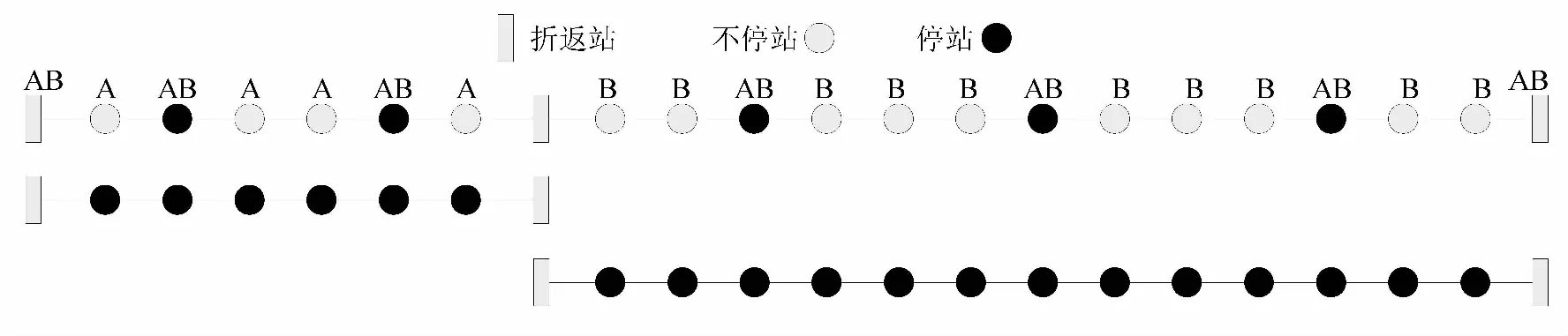
图3 停站方案示意图

(2)乘客的起终点在同一区段内，且起点站为AB类车站、终点站为A类(第1个小交路中慢车停车车站)或B类车站(第2个小交路中慢车停车车站)时，乘客有两种出行方式：直接乘坐慢车出行或先乘坐快车再换乘慢车出行，此时乘客将以出行时间最短为判断条件选择出行方式。

(3)乘客的起终点在不同区段内，且起点站为AB类车站、终点站为A类车站或B类车站时，乘客将先乘坐快车再换乘慢车出行。

(4)乘客的起终点在同一区段内，且起点站为A类车站或B类车站、终点站为AB类车站时，乘客有两种出行方式：直接乘坐慢车出行或先乘坐慢车再换乘快车出行，此时乘客将以出行时间最短为判断条件选择出行方式。

(5)乘客的起终点在不同区段内，且起点站为A类车站、终点站为AB类车站时，乘客将先乘坐慢车再换乘快车出行。

(6)乘客的起终点均为A类车站或B类车站，此时若乘客通过快慢车组合方式出行，则将至少需要换乘两次，因此将该部分乘客按照仅通过慢车出行计算。

乘客在不同类型列车之间的选择行为是一个决策制定问题，可以乘客选择不同列车看做选择不同的交通方式，便可参考计算“交通阻抗”的方法来决定出行方式。某一种出行方式的交通阻抗越小，则对乘客的吸引程度越大，乘客越倾向于选择该出行方式出行。影响交通阻抗的因素主要有票价、出行时间、出行便捷程度、舒适度以及安全性等因素。

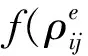
(1)

慢车直达方式的效用值可以表示为

(2)

快慢车换乘的效用函数可表示为

(3)

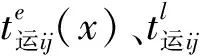
2 停站方案优化模型

2.1优化目标分析

城市轨道交通运营的参与者是乘客和运输企业两方面，在确定列车停站方案过程中，两方均对停站方案的设置提出自己的目标，即乘客追求出行时间的最小化和运输企业追求运营成本的最小化，两个目标相互影响而无法同时满足，本文将兼顾乘客的出行时间和企业运营成本两方面，建立组合交路下快慢车停站方案优化模型，制定开行方案。模型决策变量为Xi，其为1时表示c类车在i站停站，为0则不停。

2.1.1 乘客出行总时间最少

乘客利用城市轨道交通出行，最关心的便是出行时间的多少。乘客的出行时间包括等待时间、车内运行时间和停站时间3部分。

(1)站站停停车方案下，乘客的总旅行时间可表示为

(4)

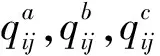
(5)

乘客的总在车旅行时间(区间运行时间及起停附加时间之和)为

(6)

乘客在列车上产生的停站时间可表示为

(7)

乘客的总出行时间可表示为

(8)

因此体现乘客利益的目标函数可表示为

(9)

另外，在使用组合交路快慢车开行方案时，乘客的总出行时间应较站站停方案有所减少，才能保证该方案的有效性，即ΔT应满足

(10)

2.1.2 运输企业成本最少

城市轨道交通作为城市公共事业的一部分，应尽量减少运输企业的运营成本以降低国家补贴，减少财政支出。企业运营成本主要包括车底固定成本、运营可变成本、停站附加成本3方面。

不考虑车辆购置成本，车底固定成本由运营中车辆的磨损、人员工资等因素组成，因此运营中车底数量的多少决定车底固定成本的大小，可以表示为

(11)

运营的可变成本与列车耗能有关，列车运行公里越大，可变成本越高，表示为

(12)

停站附加成本主要是由列车进出站时停车和起动耗能和磨损产生的，表示为

(13)

因此表示运输企业运输成本的目标函数可表示为

(14)

2.2数学模型

以乘客最小出行时间和运输企业最小运营成本建立组合交路快慢车停站方案优化模型如式(15)～(24)所示

(15)

(16)

s.t.

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

式(15)、式(16)为目标函数，其中，式(15)表示乘客的时间效益，式(16)描述运输企业的运营成本。式(17)～(24)是优化模型的约束条件，式(17)表示变量0、1约束；式(18)表示开行组合交路快慢车后乘客的出行时间减少；式(19)表示每种列车至少开行一班；式(20)表示线路的通过能力限制；式(21)表示c类车必须在线路首末站停车，式(22)～式(24)表示列车载客能力约束。

3 求解算法

3.1多目标转化为单目标

多目标函数往往不能同时达到最优解，在求解多目标函数的时候，往往将多目标函数转化为单目标函数求得满意的可行解，在转化过程中，给予多目标函数每个目标一定的权重，使得得到的单目标函数相对符合原多目标函数的预期。利用模型中第一个目标出行时间的时间价值效益，确定该目标与企业运营成本的权重关系，最终得到单目标函数模型

(25)

式中，λ为居民小时最低工资水平。

3.2遗传算法

遗传算法是启发式算法的一种，是受到达尔文进化论和遗传学中遗传因子自然选择的启发，利用随机统计理论，模拟进化过程得到最优个体的过程进行最优解搜索的方法。遗传算法是一种迭代算法，它首先从问题可能存在最优解的一个可行解集(由携带基因编码的个体组成)出发，逐代寻找演化得到问题越来越好的近似解，直到所得解完成收敛或迭代次数完成结束。

下面是算法步骤：

Step1：确定算法的迭代次数N，初始种群大小M，交叉概率Pc以及变异概率Pm。

Step2：编码与解码。

列车停站方案优化问题可釆用二进制编码方式，编码方式如图4。

图4 编码方式

染色体分为4部分，其编码长度分别为k1,k2,k3,k4，染色体总长为k1+k2+k3+k4。染色体第1部分代表c类车停站序列(1为停站，0为通过)，第2、3、4部分的十进制数值分别代表a、b、c列车的停站次数，其值ma、mb、mc与线路通过能力相关，相互关系如式(26)～(28)

(26)

(27)

(28)

式中，xj表示染色体二进制编码的第j位数值，xj=0或1。

Step3：初始化种群P0，随机产生M个可行解形成初始种群。

Step4：适应度函数的确定。采用无量纲转化后的单目标函数式(29)作为算法的适应度函数。

(29)

Step5：选择操作。选择适应度最高的个体，把群体中适应度最高的个体不进行配对交叉，而直接复制到下一代中，以保存条件最好的个体。

Step6：交叉操作。采用单点交叉。首先，对染色体进行随机配对，并以一定的概率选择配对好的染色体进行交叉操作。对要进行交叉操作的染色体组随机选择交叉点的位置，互换交叉点之后的基因。

Step7：变异操作。在群体中所有个体的码串范围内随机地确定基因位置，以事先设定的变异概率来对这些位置的基因值进行变异。

Step8：重复以上(4)～(7)的操作，直至达到终止条件结束。

4 案例分析

4.1线路特征

选取A市某超长线，线路全长66.4 km，共有车站35个，中间设置一处折返站，折返站两端小交路线路长度分别为26.7 km和39.7 km，平均站间距1.90 km。

区间断面客流量的分布情况如图5，沿线各车站上下车客流如图6，断面客流不均衡系数达到0.57，客流存在较为明显的分段特征，中间折返站(11站)两端均出现较大的向心客流且在部分车站上下车较为集中，适宜实施长达交路与分段衔接的组合交路下的快慢车开行方案。

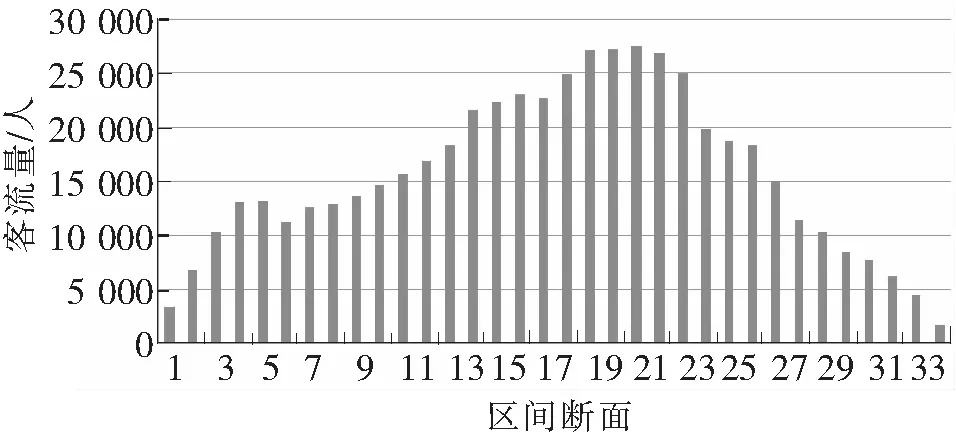
图5 线路区间断面客流量

图6 沿线各车站上下客客流

4.2停站方案的生成

4.2.1 模型参数确定

根据线路OD客流和车站线路通过能力限制，可以大致确定优化时段内的发车次数。A区段内最大最小断面客流量分别14 692人和3 435人，B区段内最大最小断面客流量分别为27 494人和1 696人，因此根据列车载客量大小(310人/车×6车/编组=1 860人/编组)及线路通过能力限制，可初步确定各区段总发车次数的取值范围为10～24。

模型中相关参数取值，见表1。

表1 模型参数取值

4.2.2 模型求解过程

模型求解共分为两步，一是将模型中多目标模型转化为单目标，二是利用遗传算法求解该单目标模型。求解过程如下：

(1) 确定算法迭代次数N为200，初始种群M取200，交叉概率取1，变异概率Pm取0.01。

(2) 染色体编码采取4.2.2节中分析的第一种方法，染色体前35位表示停站方案，35～40位、41～45位、46～50位分别表示a、b、c列车的开行次数。

(3) 适应度函数。根据居民小时最低工资水平转化出行时间后得到算法的适应度函数式

(30)

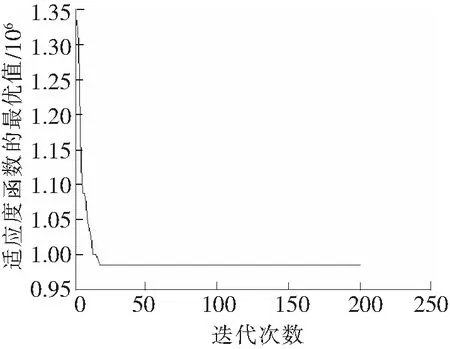
图7 最优适应度函数收敛曲线

(4) 模拟计算过程。将模型相关参数导入算法中进行模拟计算。优化过程中最优综合评价值的变化如图7所示，从图7中可以看出，适应度函数曲线在迭代次数为17时即达到了收敛，此时T=102 471，ma=12，ma=6,ma=9,适应度为9.847 7×105。

4.2.3 停站方案分析

计算结果如表2所示，结果显示当该时段内a,b,c3种列车的发车次数分别为12次，6次，9次时，目标函数综合评价值(适应度)达到最优，为9.847 7×105；对应的快车停站方案为：[10000 01000 00010 00100 00110 00001 00001 01100 00110 01001]。

表2 停站方案计算结果

从计算结果可以看出，长大交路上的快车共停站6处，6处车站均与沿线上下客流量较大，平均运距长的车站相一致，可以很好地满足其客流集散需求。对比线路OD表发现，快车所停车站之间的客流交换量大，说明该组合交路快慢车方案可以缩短很多乘客的出行时间。

5 结束语

超长线停站方案的好坏很大程度上影响城市居民的出行质量，在详细分析超长线客流时空分布、乘客出行选择行为以及运输企业运营成本构成的基础上，提出了一种在组合交路下超长线停站方案的制定方法，并通过一个案例验证了模型的有效性。

另外在部分问题上的研究还不够完善，后续可作深入研究。

(1) 在对乘客进行出行行为分析时，为简化计算，假设乘客仅考虑在不同列车间换乘一次的情况，对二次换乘不予考虑，因此后续可深入研究乘客的出行阻抗函数，详细分析乘客的出行行为。

(2) 模型的建立基于仅开行小交路站站停列车和大交路跨站停列车两种列车，后续可尝试开行多种类型列车，可以增大列车满载率，更好地满足乘客出行需求。

[1] Assad A. Class of train-scheduling problems [J].Transportation Scienoe，1982(16):281-310.

[2] Salzbom E， J M. Timetables for a suburban rail transit system [J]. Transportation Science， 1969 (3):279-316.

[3] Vijayaraghavan T A S. Vehicle scheduling in urban transportation with quick and cut trip insertions for fleet reduction [J]. Transportation Planning and Technology,1988,12(2):105-120.

[4] 方蕾，庞志显.城市轨道交通客流与行车组织分析[J].城市轨道研究，2004(5):42-44.

[5] 张钰. 重庆市轨道交通超长线运输组织研究[D].成都：西南交通大学， 2012.

[6] 张越. 城市轨道交通 “超长线” 行车组织优化[D]. 西安：长安大学, 2008.

[7] 屈明月，黄树明.城市轨道交通快慢车方案研究[J]. 铁道运输与经济， 2012， 34(4): 79-82.

[8] 王琳. 城市轨道交通快慢车运营组织研究[D]. 北京：北京交通大学， 2013.

[9] 郑锂，宋瑞，何世伟，等.城市轨道交通跨站停车方案优化模型及算法[J].铁道学报，2009，31(6): 1-8.

[10] 谭小土. 城市轨道交通快慢车运行组织研究[D]. 成都：西南交通大学， 2014.

[11] 熊贻辉. 市域线快慢车组合运营模式研究[D]. 成都：西南交通大学， 2012.

[12]靳能法. 城市轨道交通运营组织相关问题研究[D]. 成都: 西南交通大学交通运输与物流学院， 2010.

[13]祝晓波. 市域轨道交通快速线开行方案研究[D]. 成都：西南交通大学， 2009.

[14]李俊芳. 基于运输能力的城市轨道交通运输组织方案评价研究[D].成都：西南交通大学， 2010.

[15]郭钰.城市轨道交通列车停站方案优化研究[D].北京:北京交通大学，2009.

OptimizationofStopSchedulePlanforUltra-longLineinUrbanRailTransitBasedonCombinedTrainRouting

ZhangYao

(Chengdu Institute of Planning &Design, Chengdu 610031, China)

At present, China urban rail transit network continues to improve, the line density increases and the length of the line grows. With large-scale planning and construction of ultra-long lines, it is noteworthy that lines present a complex spatial and temporal distribution of passenger flow, and longer average transport distance, which requires transport companies to develop a more rational and efficient operation scheme. This paper focuses on the stop schedule plan of urban rail transit express/local train based on combined train routing of single-long and segments routing scheme optimization. Taking full account of passenger traffic characteristics and the basic elements of organization of train operation, this paper proposes a 0-1 integer programming model based on minimum travel time for passengers and minimum corporate transportation costs, and designs algorithms to solve the model.

ultra-long lines; express/local train; stop schedule plan; genetic algorithm

U231+.2; U292

： A

： 2095-0373(2017)03-0099-08

2016-08-04责任编辑:车轩玉

10.13319/j.cnki.sjztddxxbzrb.2017.03.19

张要(1991-), 男, 助理工程师,主要从事交通运输规划与管理的研究。E-mail: 810997609@qq.com 张要.组合交路条件下城市轨道交通列车停站方案优化研究[J].石家庄铁道大学学报:自然科学版,2017,30(3):99-105.