Duffing方程参数对微弱信号检测效果的影响和分析
2017-09-22志宏
, , 志宏
(石家庄铁道大学 机械工程学院,河北 石家庄 050043)
Duffing方程参数对微弱信号检测效果的影响和分析
赵波,杨绍普,赵志宏
(石家庄铁道大学 机械工程学院,河北 石家庄 050043)
目前利用Duffing方程检测微弱的未知信号都是选择一组固定的参数。由于Duffing方程对初值的敏感性,使得参数的选择对检测效果产生很大的影响。针对这种情况,分析了Duffing方程的参数和初值之间的关系。由参数和初值之间的关系,分析了不同的参数对检测效果的影响。验证了目前方程参数的优越性。
Duffing方程;方程参数;检测效果
0 引言
随着科学技术的发展,越来越多的机械设备被运用到生活生产中。机械设备的故障,不仅会造成严重的经济损失,甚至会造成巨大的人员伤亡。由于早期的机械设备故障信号都是非常微弱的,因此微弱信号的检测具有非常重要的意义。微弱信号检测技术是近几年迅速发展起来的,利用电子学理论、信息理论和物理学方法来达到强噪声背景下的微弱信号检测[1]。传统微弱信号的检测,都是基于线性和确定性的系统[2]。传统方法以时域和频域为主,例如小波变换和频谱分析[3-6]。传统方法要求较高的信噪比,需要对信号进行预处理,局限性较大。随着非线性动力学的发展和混沌理论研究的深入[7-9],人们开始利用非线性动力学分析故障零件的动力学行为,揭示故障产生、发展的一般规律[10]。混沌现象主要是非线性系统的时间演化行为。混沌系统是终极端敏感的依赖于初始状态的系统。在混沌运动中,初始值非常靠近的两条轨道,随时间的发展会指数分离。这也就是说,对轨道的长期行为不可能做出准确的预测。混沌方法具有对微弱信号的敏感性和抗噪能力比较强的优点,是一种比较有前景的微弱信号检测方法。常见的混沌振子系统有Duffing-Holmes型混沌振子[11]、双耦合Duffing振子系统[12]、Duffing振子和Van der pol振子耦[13]等。不同的混沌振子有不同的特性。本文是基于Duffing-Holmes型混沌振子的参数分析,分析了系统参数和初值的关系。从不同的参数对系统临界点相图的突变性和混沌区间的保持性两方面进行分析。通过改变系统的参数,利用Matlab仿真进行这两方面性质的分析,验证了阻尼系数c=0.5的优越性。
1 Duffing-Holmes型混沌振子检测微弱信号的原理
1.1Duffing-Holmes型混沌方程
Duffing-Holmes型混沌方程如下
(1)
式中,c为阻尼系数;Fcost为摄动信号。
从理论上来讲,系统的解在相空间中,随F/c值的改变而改变。F/c从0逐渐增加时,系统的解在相空间的轨迹为偶阶次谐分岔,此时系统按外加周期力的周期或其倍周期振荡;当F/c增加到临界值时,出现同宿轨迹,产生Smale马蹄意义下的混沌运动;当F/c进一步增加时,系统将出现倒奇阶次谐分岔,最后以外加周期力的频率进行大尺度的周期振荡,此后F/c进一步增大时,该周期外轨仍然存在,只是形状有所变化。
1.2Duffing-Holmes型混沌振子检测微弱信号的原理
加入微弱待测信号的Duffing方程为
(2)
式中,Fr为摄动力幅值;A为待检测信号的幅值;φ为摄动信号和待测信号的相位差;Δω摄动信号和待测信号的绝对频差。其中A<
Frcost+Acos((1+Δω)t+φ)=F(t)cos(t+θ(t))
(3)
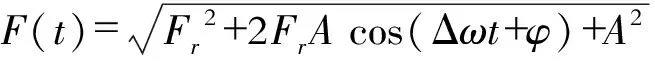
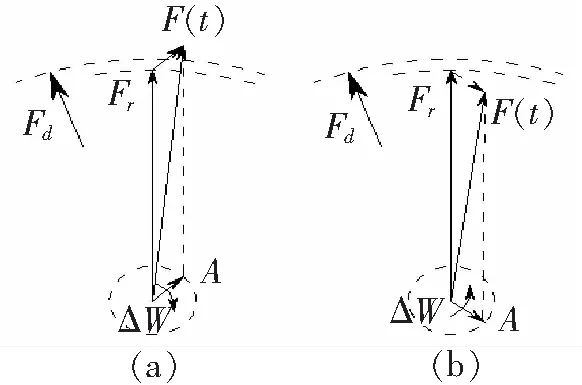
图1 等效驱动力变化过程
因为A<
2 Holmes-Duffing方程振子的参数和初值的关系
因为混沌系统对于微弱信号的检测是由于系统对初值或参数的敏感性决定的。不同的参数具有不同的检测性能,也适用于不同环境下的信号检测。从参数和初值之间的关系,不同参数对系统的检测性能具有哪些影响,从这两方面分析,来确定系统的参数,是基于Holmes-Duffing方程振子的参数分析。
方程振子如下
(4)
(5)
将上面两个方程相除消去f可得
(6)
方程(5)为方程(4)求导所得,方程(6)由方程(4)和方程(5)联立所得,所以方程(4)的解既是方程(5)的特解,又是方程(6)的解。方程(4)的参数通过变换成为方程(6)的初值,可以看到,在该方程(4)中初值与参数的敏感性是一致的。
3 Holmes-Duffing方程振子的参数对检测效果的影响和分析
目前,基于Holmes-Duffing方程振子的参数,默认的参数c=0.5。下面就c的取值,对系统性能的影响进行分析,主要从系统临界点相图的突变性和混沌区间的保持性两方面进行分析。
系统临界点相图的突变性是指系统由混沌状态立即进入大周期状态[14],突变性代表混沌检测性能的精度。在检测信号的过程中,若相图发生了突变,说明待测信号中含有与摄动信号频率一致的微弱信号,下一步就是检测未知信号的大小,通常的做法就是反向调整摄动力的幅值,使相图又回到临界混沌状态。但是在具体操作的过程中,可能由于幅值调整的幅度过大,越过混沌区间,这就导致误判。因此混沌区间应该保持一定的“厚度”,这就是混沌区间的保持性。下面通过调整阻尼的值就这两方面的性能进行分析。设c=0.1、0.4、0.5、0.6、0.9这5个参数进行分析。使用ode45仿真,初值为X=[0 0],摄动力的幅值步长为0.001。本文只是提供一般方法,具体需要多大的精度可以进一步计算。
当c=0.1时系统的分岔图如图2所示。从分岔图可知,并没有明显的混沌与大周期的界限,混沌区间几乎没有,因此c=0.1几乎没有价值。
当c=0.4时系统的分岔图如图3所示。可以看到阈值约为0.671,混沌区间厚度约为0.38,因为选取的摄动力幅值步长为0.001,所以图3分辨出的最高精度为0.001,可以看到混沌和大周期之间具有明显的界限,具有非常好的检测性能。
当c=0.5时分岔图如图4所示。临界阈值约为0.825,厚度约为0.45。具有良好的混沌区间保持性和非常明显的混沌与大周期的界限。
当c=0.6时分岔图如图5所示。临界阈值约为0.984,厚度约为0.15。混沌区间保持性一般较c=0.5时差距较大,但具有非常明显的混沌与大周期的界限。
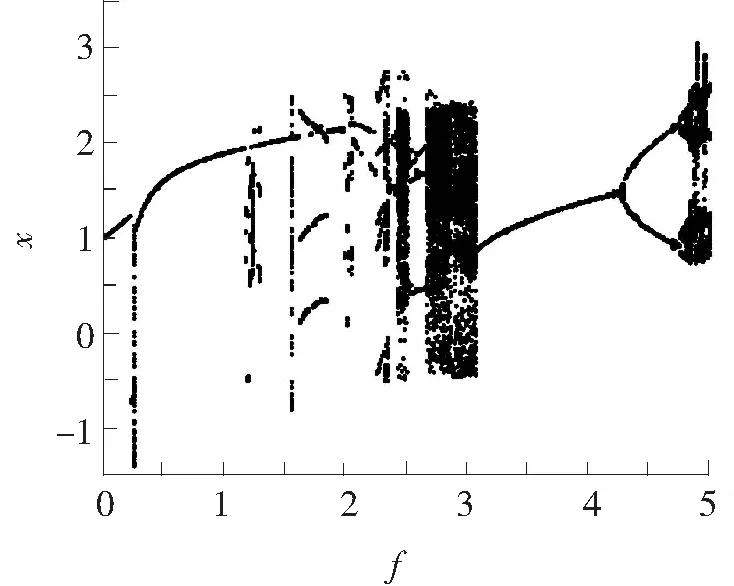
图2 c=0.1时的分岔图
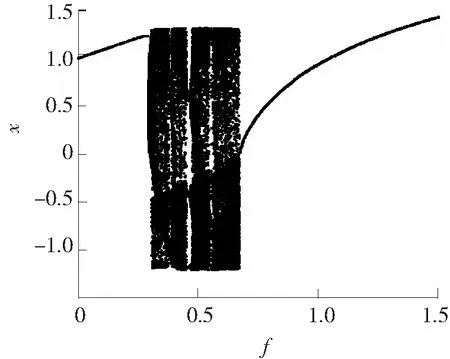
图3 c=0.4时的分岔图
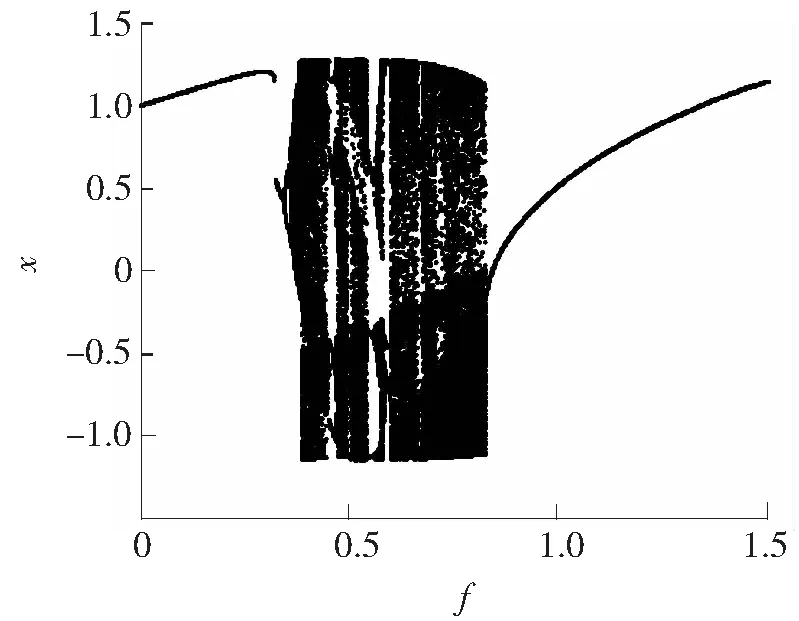
图4 c=0.5时的分岔图
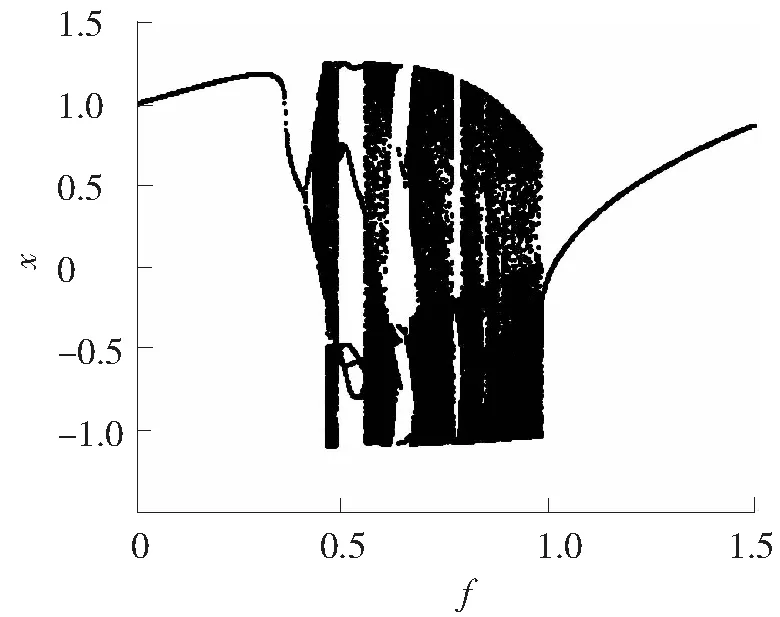
图5 c=0.6时的分岔图
当c=0.9时由图6,图7可知,并没有明显的界限,混沌区间几乎没有,因此c=0.9几乎没有价值。
通过以上分析可以发现,无论是从混沌区间的保持性还是临界点的突变性分析,c=0.5都表现出良好的性能。
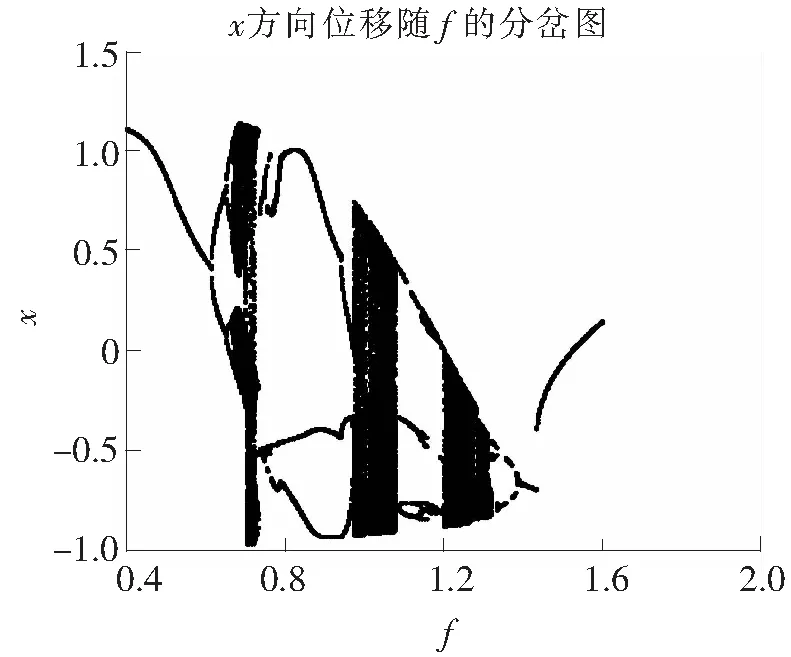
图6 c=0.9时的分岔图
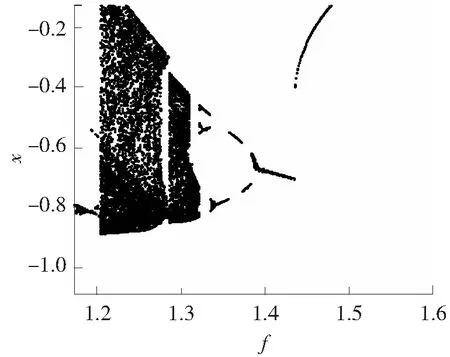
图7 c=0.9时的放大分岔图
4 结论
通过分析Duffing方程的参数和初值之间的关系,证明了参数和初值的一致性。通过改变方程参数,在混沌区间保持性和临界点的突变性这两方面性能进行了分析,证明了参数c=0.5的优越性。为参数的选择提供了一定的参考。由于微弱信号的检测肯定会掺杂噪声,在进行性能分析时,没有加入噪声,有一定的局限性,未来还需在这方面进行分析。
[1] 朱来普,张陆勇,谢文凤.基于Duffing混沌振子的微弱信号检测研究[J].无线电工程,2012,42(1):17-20.
[2] 谢 涛,魏学业.混沌振子在微弱信号检测中的可靠性研究[J].仪器仪表学报,2008,29(6):1265-1269
[3]周小勇,叶银忠. 小波分析在故障诊断中的应用[J]. 控制工程,2006(1):70-73.
[4]WangXY,FuZK.Awavelet-basedimagedenoisingusingleastsquaressupportvectormachine[J].EngineeringApplicationsofArtificialIntelligence, 2010, 23(6): 862-871.
[5]HassaniH,XuZ,ZhigljavskyA.Singularspectrumanalysisbasedontheperturbationtheory[J].NonlinearAnalysis:RealWorldApplications, 2011, 12(5): 2752-2766.
[6] 孙英侠,李亚利,宁宇鹏. 频谱分析原理及频谱分析仪使用技巧[J]. 国外电子测量技术,2014(7):76-80.
[7] 陈予恕,曹登庆,吴志强. 非线性动力学理论及其在机械系统中应用的若干进展[J]. 宇航学报,2007(4):794-804.
[8] 王俊国,周建中,付波,等. 基于Duffing振子的微弱信号混沌检测[J]. 电子器件,2007(4):1380-1383.
[9]MetzgerMA.Applicationsofnonlineardynamicalsystemstheoryindevelopmentalpsychology:Motorandcognitivedevelopment[J].NonlinearDynamics,Psychology,andLifeSciences, 1997, 1(1): 55-68.
[10] 顾晓辉.含典型故障的滚动轴承—转子系统非线性动力学行为分析[D].石家庄:石家庄铁道大学,2014.
[11] 孙立莹,周璇,常志英. 基于Duffing-Holmes混沌振子的微弱信号检测方法[J]. 舰船科学技术,2012,34(z1):38-41.
[12] 王晓东,赵志宏,杨绍普.基于耦合Duffing振子的微弱故障信号检测[J].噪声与振动控制,2016,36(3):174-178.
[13]王晓东, 杨绍普, 赵志宏.Duffing振子和VanderPol振子耦合的动力学行为分析[J]. 石家庄铁道大学学报: 自然科学版, 2015, 28(4): 53-57.
[14] 范剑,赵文礼,王万强. 基于Duffing振子的微弱周期信号混沌检测性能研究[J].物理学报,2013,62(18):1-5.
DuffingEquationParametersInfluenceontheEffectofWeakSignalDetectionandAnalysis
ZhaoBo,YangShaopu,ZhaoZhihong
(School of Mechanical Engineering,Shijiazhuang Tiedao University,Shijiazhuang 050043, China)
Using Duffing equation to detect weak unknown signal is done by selecting a set of fixed parameters. Due to the sensitivity of Duffing equation to the initial value, the choice of parameters has a very big effect on the detecting effect. In view of this situation, this paper analyzes the relationship between the parameters and initial value of the duffing equation, and the influence of different parameters on the detection effect, thus the superiority of the present equation is verified.
Duffing equation;equation parameters;test results
O415.5
: A
: 2095-0373(2017)03-0039-04
2016-06-19责任编辑:车轩玉
10.13319/j.cnki.sjztddxxbzrb.2017.03.08
国家自然科学基金(11172182,11472179,11227201);河北省研究生创新项目(yz2016003)
赵波(1991-),男,硕士研究生,主要从事故障诊断的研究。E-mail:386547260@qq.com 赵波,杨绍普,赵志宏.Duffing方程参数对微弱信号检测效果的影响和分析[J].石家庄铁道大学学报:自然科学版,2017,30(3):39-42.
