一种ECVT有限元自动剖分方法

， ， ，

(1.广西大学 计算机与电子信息学院，广西 南宁 530004；2.石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043)

一种ECVT有限元自动剖分方法

邹星星1，赵进创1，傅文利1，马增强2

(1.广西大学 计算机与电子信息学院，广西 南宁 530004；2.石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043)

ECT三维传感器场域剖分是当前ECT直接三维成像研究的关键问题，提出一种三维有限元自动剖分方法并得到结果验证。采用四面体作为剖分单元，利用Delaunay四面体剖分算法反复迭代实现三维实体自动剖分；为清晰显示剖分图像，结合画家算法对网格进行消隐处理。仿真结果表明，随着迭代次数增加，剖分精度提高，其剖分时长也会相应增加。根据需求剖分精度设置迭代次数，能有效的剖分传感器场域，实现了三维场域自动剖分，为计算三维敏感场从而提高ECT三维成像精度奠定基础。

电容层析体积成像；有限元；自动剖分

0 引言

电容层析成像技术(Electrical Capacitance Tomography)基于奥地利科学家J.Radon于1917年提出的图像重建理论(即Radon变换及其逆变换)，通过放置在被测管道周围的传感器阵列获取被测场域不同观测角度下的多个电容测量值(即ECT正问题)，以此为投影数据，采用适当的图像重建算法重建被测区域内介质分布(即ECT逆问题)。由于其适用范围广、响应速度快、测量方式非侵入、结构较简单、成本较低，具有十分广阔的应用前景，是过程层析成像技术(PT)的主流之一[1]。

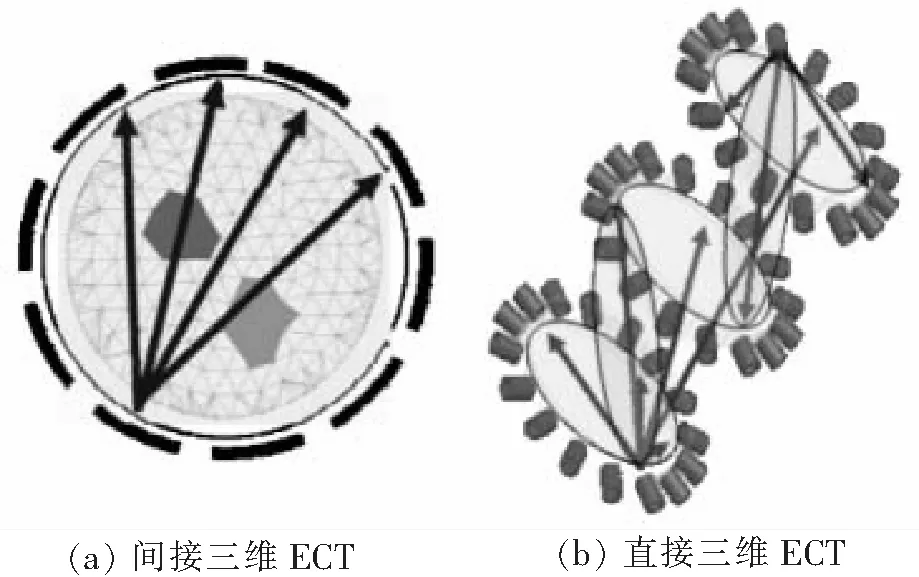
图1 传感器测量方式示意

目前较为成熟的三维电容层析成像主要通过获取多个二维断层图像进行三维重建[2]，以此获取三维图像。然而由于间接三维成像轴向分辨力低，研究者们提出在三维空间上进行测量，利用测量得到的信息直接进行三维成像。图1给出传统电容层析三维成像(间接三维ECT)和电容层析体积成像(直接三维ECT)的传感器测量方式。①传统电容层析三维成像系统同层极板测量，②电容层析体积成像 系统同层、异层极板对测量。

2006年，R.wajman和R.Banasiaka等采用迭代的线性反投影算法，证明了电容层析体积成像系统在重建图像质量上优于间接三维ECT系统[2]，电容层析体成像日渐成为研究热点。2012年，颜华和宁秀坤等[3]对12极板ECVT系统进行图像仿真研究。一直以来，研究者们相应提出了多种二维ECT有限元网格自动剖分算法。1983年，Yerry M A 和 Shephard M S等[4]人提出栅格法实现了二维有限元场域网格剖分，但其精度低且耗时长。1996年，郑大宇和周跃发[5]提出映射法剖分二维有限元场域，提高剖分精度。1998年，肖化和严杰等[6]提出几何分解法，进一步提高了二维有限元场域的剖分精度。陈德运和杨从晶等[7]于2003年提出节点连元法，获得较高质量的剖分单元同时减少剖分时长。此后二维有限元剖分算法日渐完善，并取得较好效果。由于三维域特殊性，剖分方法由平面域向三维域扩展一直难以实现。为有效求解ECT三维传感器场域电场问题，从而直接获取三维敏感场进行三维图像重建，最终提高ECT三维重建图像轴向分辨力，本文针对ECT三维传感器场域特性以及适用剖分单元选取，改进Watson提出的基于Delaunay四面体剖分算法，采用迭代方式提高场域剖分精度，实现ECT三维传感器场域自动剖分。

1 ECVT有限元分析

假定传感器场域内无自由电荷分布，即该电场为似稳场。根据麦克斯韦方程，获得传感器场域内电势分布方程

(1)

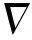
(2)

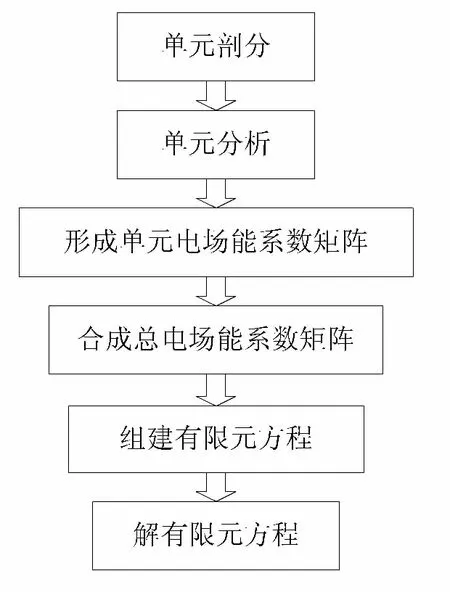
图2 静电场有限元分析流程图

由于无法用解析法求解式(2)，通常采用数值法中的有限元法进行求解。即依据变分原理将式(2)的边值问题化为相应的变分问题，然后利用剖分插值将变分问题转化为普通多元函数的极值问题，最终归结为一组多元的代数方程组，用迭代法或直接法求解。静电场有限元方法步骤如图2所示[8]。

同二维ECT系统分析一致，三维ECT系统仍需采用有限元方法对传感器场域电场变分问题进行求解，而单元剖分作为有限元分析首要步骤变得尤为重要。

2 ECVT传感器场域剖分

有限元法分析是将传感器场域即连续场离散为有限个子域(单元)，由这些仅在节点处互相连接的子域的集合代表整个解域。场域剖分直接影响计算结果的精度，因此在求解ECT三维传感器场域过程中，选择适当的单元和插值函数是决定性步骤之一。

2.1剖分单元选取

有限元方法生成技术，发展至今，方法颇多[9]。通常在进行场域剖分之前，首先需要确定剖分采用的单元类型。用于三维场域有限元分析的单元类型多种多样，其中常用的三维单元类型如图3所示，有四面体、五面体、六面体。

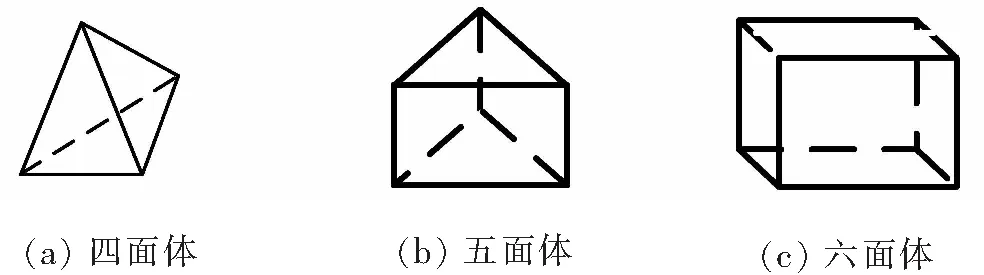
图3 三维场域剖分单元类型

剖分所采用的单元的几何形状、节点个数与其节点的配置情况取决于插值函数的选取。插值函数构造方法分为Lagrange型和Hermite型，一类是单元的节点参数中只包含场函数的节点值，另一类单元的节点参数中，除场函数的节点值外，还包含场函数导数的节点值。故Hermite型单元构造复杂，对某些问题甚至无法实现，而Lagrange型单元构造和实现相对简单，故采用此类型单元。场域单元节点越多，敏感场精度越高，随之计算时间越长。考虑到ECT传感器通常为圆柱体，形状对称，为确保满足剖分精度条件下尽量减少剖分时间，本文提出的方法以4节点四面体为剖分单元。

2.2剖分算法框架

由于以四面体剖分单元，且Delaunay三角剖分算法是最优三角剖分算法，故采用Watson提出的经典Delaunay作为剖分算法。然而由于其三维空间剖分算法在应用到ECT三维传感器场域剖分的仿真过程中存在网格质量差的问题，故本算法针对特定剖分对象即ECT传感器场域，在Watson的逐点插入法基础上进行迭代。即当插入一个新点时，如果该点落在某个四面体内，则将此四面体的4个顶点与该点相互连接，从而形成4条新的边。然后根据Delaunay三角网格优化的准则进行优化，从而形成高质量三角网；若该点落在四面体边上，则删除该边。以此插入新点并反复迭代，直至满足迭代终止条件。

具体步骤如下：

(1)给出迭代次数，接着对三维实体的边、面进行离散形成Delaunay三角形网络；

(2)这些面上所有节点的集合即三维实体Delaunay四面体化的初始点集P；

(3)对P进行Delaunay四面体化，构成了三维实体Delaunay初始四面体剖分；

(4)判断是否超出迭代次数，若没有超出迭代次数，则返回继续离散划分；

(5)否则采用画家算法对剖分网格进行消隐处理，绘出较强立体感的网格图。

3 仿真结果与分析

本文的方法在Windows环境下，基于Matlab平台进行仿真实验。根据ECT直接三维传感器场域，取直径为1，高度为2.5的圆柱体模型作为剖分对象，分别设置迭代剖分次数为0次(即未经迭代处理的Delaunay四面体化剖分)、10次、100次、200次进行四面体单元自动剖分，以此验证本文方法有效性。图4给出了前人算法以及本文算法在ECT直接三维传感器场域剖分效果图。

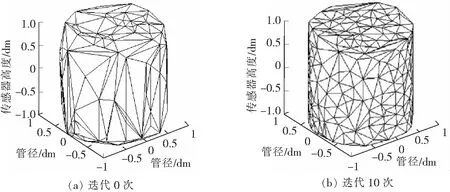
图4 前人算法与本文算法剖分图

由图4可知，针对ECT三维传感器场域，本文算法较前人算法提高了剖分单元质量以及剖分精度。同时，增加迭代次数仿真证明，随着迭代剖分次数增加，剖分单元质量以及剖分精度也会相应提高。图5给出了不同迭代次数下自动剖分图。

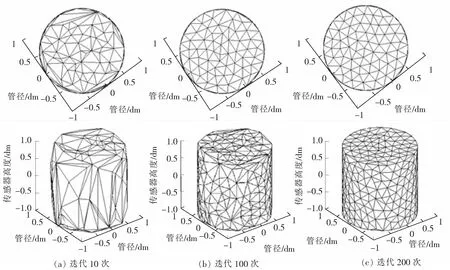
图5 不同迭代次数下自动剖分图

由图5可知，迭代剖分次数越多，剖分越细，生成的有限元单元数就越多，有限元解的精确度越高。图6给出了不同剖分次数与生成单元结点数、单元数关系。

根据图6可知，迭代剖分次数增加，剖分的单元数与结点数增加。然而由于迭代剖分次数增加，导致剖分计算量增大，计算时间变长。图7给出了迭代次数与剖分时间关系图。

实际验证证明，本文提出的方法能够有效的对电容层析成像三维电场场域进行四面体单元自动剖分，且剖分单元质量良好，能够满足后续电容层析成像有限元分析、计算的要求。

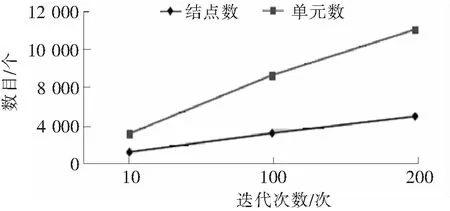
图6 迭代次数与生成结点数、单元数关系图

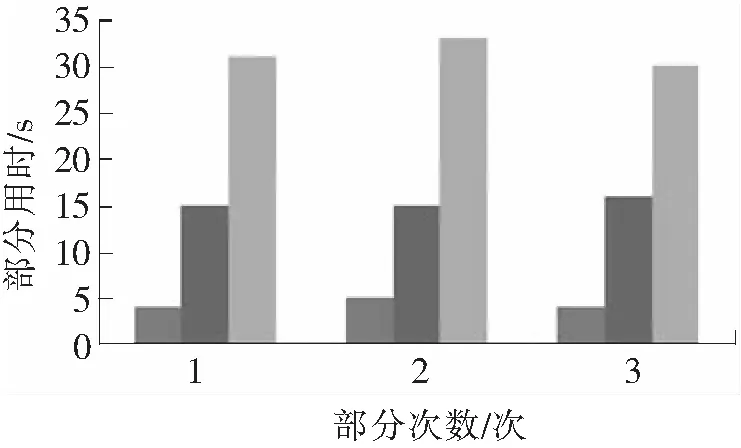
图7 迭代次数与剖分时间关系图

4 结语

本文针对ECVT成像系统中三维电场场域提出一种三维有限元自动剖分方法，是运用有限元方法求解三维电场场域电位分布的关键步骤。实验结果表明，本文方法能够实时有效的将三维ECT传感器场域剖分为多个四面体单元，对ECVT有限元正问题分析研究具有较高实用价值。本文下一步的工作在自动剖分的基础上研究三维ECT传感器场域自适应剖分方法。

[1]赵进创，傅文利，李陶深，等. 电容层析成像喜用三维图像重建的研究[J].计算机应用研究, 2004, 21(4):246-247.

[2]Wajman R, Banasiak R, et al. Spatial imaging with 3D capacitance measurements[J].Measurement Science and Technology, 2006,17(8):2113-2118.

[3]颜华,宁秀坤,王伊凡,等. 12极板直接三维ECT图像重建仿真[J]. 沈阳工业大学学报, 2012,34(5):542-548.

[4]Yerry M A. Shephard M S. A modified quad tree approach to finite element mesh generation[J]. IEEE Computer Graphics & Applications, 1983,3(1):39-46.

[5]郑大宇,周跃发. 超限映射法在二维有限元网络生成中的应用[J]. 黑龙江商学院学报：自然科学版, 1996,12(3):37-41.

[6]肖化,严杰,保宗悌. 有限元在电容层析中的应用研究[J].应用科学学报,1998, 16(2):170-175.

[7]陈德运,杨从晶,郑贵滨,等. 电容层析成像系统传感器场域新的剖分方法及图像重建[J].传感技术学报, 2003(4):409-414.

[8]杜群贵. 三维实体有限元网格自动Delaunay剖分[J]. 华南理工大学学报, 1996,24(9):46-49.

[9]李海峰，吴冀川，刘建波，等. 有限元网络剖分与网格质量判定指标[J]. 中国机械工程，2012，23(3):368-377.

AMethodofFEMSelf-OrganizingMeshGenerationforECVT

ZouXingxing1,ZhaoJinchuang1,FuWenli1,MaZengqiang2

(1.College of Computer&Electrical Information, Guangxi University, Nan’ning 530004,China;2. School of Electric and Electronic Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

As three-dimensional sensor field mesh of ECT is a key issue in direct 3D ECT currently, a method of 3D FEM self-organizing mesh generation is proposed. The method adopts tetrahedron as split unit, and uses Delaunay triangulation algorithm for auto meshing 3D solid. Finally, the painter algorithm is used to process grid blanking. Simulation results show that with the increase in the number of iterations, mesh accuracy is improved while more time is spent. Setting iteration according to the precision of mesh can effectively mesh the sensor field, achieving the three-dimensional auto meshing, which provides basis for calculating the three-dimensional sensitivity field in order to improve the accuracy of three-dimensional imaging of ECT.

ECVT;FEM;self-organizing

TP391

： A

： 2095-0373(2017)03-0106-05

2016-05-03责任编辑:刘宪福

10.13319/j.cnki.sjztddxxbzrb.2017.03.20

国家自然科学基金(61362025)

邹星星(1993-)，女(侗族)，硕士研究生，主要从事电学成像、图像处理研究。E-mail:vivi_zou0_0@hotmail.com

赵进创(1968-)，男，博士，教授，主要从事电学成像技术，数字图像处理研究。E-mail:zhaojch@gxu.edu.cn 邹星星，赵进创，傅文利，等.一种ECVT有限元自动剖分方法[J].石家庄铁道大学学报:自然科学版,2017,30(3):106-110.