基于Bayes的导弹加速贮存试验参数估计

卢明章，宋永军，赵海军



基于Bayes的导弹加速贮存试验参数估计

卢明章，宋永军，赵海军

（中国人民解放军91049部队 博士后科研工作站，山东 青岛 266102）

目的研究导弹加速贮存寿命试验中的参数估计问题。方法拟在小子样的情况下，设计一系列反复连续的导弹加速贮存仿真试验，将前一试验的结果作为之后试验的先验分布，基于Bayes方法建立导弹加速贮存寿命模型，给出贮存寿命参数估计算法，探讨导弹贮存可靠性评估方法。结果算例给出贮存寿命参数的极大似然估计，利用RBA方法对参数估计值进行降偏修正，得出参数的修正似然估计值，给出导弹贮存可靠度。给出的参数估计在均方误差意义下结果较优。结论序列试验Bayes算法易行、精度高，可有效对导弹贮存可靠性进行评估。

导弹；贮存试验；极大似然估计

导弹在经过一段时间的贮存、检测和故障修复等状态后，其内部材料性能的变化是导致贮存可靠性下降的主要原因[1—2]。由于工业部门的工作重点放在导弹的任务飞行可靠性，其环境试验中心主要是开展“导弹飞行环境模拟与验证试验”，而针对导弹贮存环境适应性研究较少[3]，这就需要研究恶劣环境下的导弹加速贮存寿命试验，对导弹的贮存可靠性进行有效评估。迄今为止，我国对原材料、元器件的加速贮存试验已经有了一些研究成果及应用信息，国内有专家在导弹的加速贮存试验方面做了探索性的工作，并给出了整机（伺服机构）加速贮存试验的工作程序[4]，但真正开展整机加速贮存试验的工程应用不多，缺乏相应的试验方法[5]。

文中拟在故障数据有限的情况下，设计一系列反复连续的导弹加速贮存寿命试验，基于Bayes估计，将前一试验的结果作为之后试验的先验分布，得出导弹贮存寿命的参数估计。该研究对小子样情况下（对导弹进行统计试验时，由于受到样本少、试验成本高、且贮存期比较长，一般不可能对其进行连续不断的检测，从而导致试验数据较少）如何对导弹贮存寿命进行有效的评估具有实际意义。

1 加速贮存寿命试验方法

加速寿命试验的最优设计包括：在给定应力范围、样品数量等条件下，如何确定加速应力水平的大小及如何分配各应力水平下样品的数量，以获得对可靠性指标更准确的估计[6—7]。Bayes方法解决统计问题的思路不同于经典统计方法，其显著特点就是在保证决策风险尽可能小的情况下，尽量应用所有可能的信息，包括现场试验的信息、现场试验前的信息，而真正的现场试验数据可以是很少的[8—9]。

导弹加速贮存寿命试验如图1所示。一共进行个加速贮存试验，每个试验中包括个子试验。每次试验之后，未淘汰装备贮存可靠度提升，通过这一系列反复的试验，可以给出导弹贮存可靠度。利用每次试验中第子试验中的寿命密度函数()，可以计算出贮存可靠度()。将每次加速贮存试验得出的可靠度值连起来，就可以建立贮存寿命模型。加速贮存寿命试验步骤如下：假定导弹装备寿命服从威布尔分布；试验目的是为了得出故障率和平均剩余寿命MTTF，在小子样条件下，合理的参数值是未知的，就需要求出其后验分布，进行参数估计；在小子样条件下，很难保证参数估计值的无偏性，要对估计值进行修正，以保证可信性；基于Bayes理论，在试验中，上一阶段得出的后验分布作为下一阶段试验的先验分布。

图1 加速贮存试验

2 导弹贮存寿命模型

2.1 参数分布

导弹加速贮存试验符合浴盆曲线中的早期故障规律，通常用威布尔分布来描述这一时期部件寿命分布规律，此时<1，威布尔分布的失效率是单调递减的[10]。因此，假设部件寿命服从威布尔分布(,)，部件寿命的概率密度函数为：

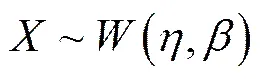
满足≥0，>0，0<<1时，

部件寿命的期望值为()，平均剩余寿命MTTF（Mean Time to Failure）为：

(2)

代入式(1)，可得期望值为：

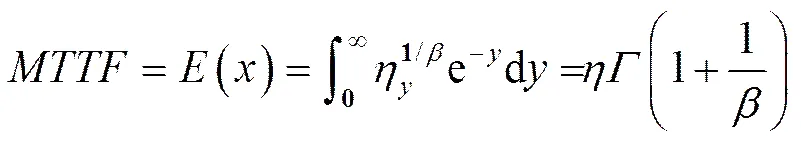
此外，可得方差为：

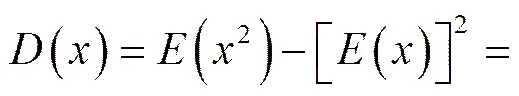
(4)

将式(2)代入式(4)，可得：

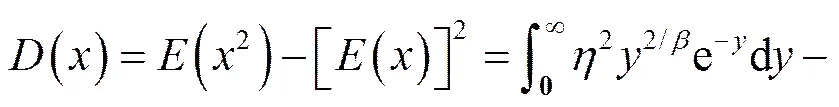
因此，贮存寿命参数的概率密度函数()可以通过下列步骤得出：

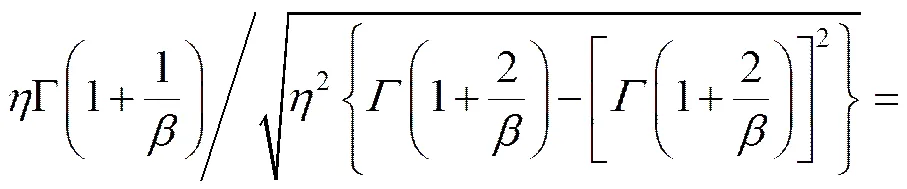
(6)

若是总体均值的一个无偏估计，是总体方差的无偏估计，由公式可计算出的值。既然，，，根据式(6)，和的测量值可用来推导。此外，根据式(1)，利用平均剩余寿命可计算出参数的值，参数和可以得出：

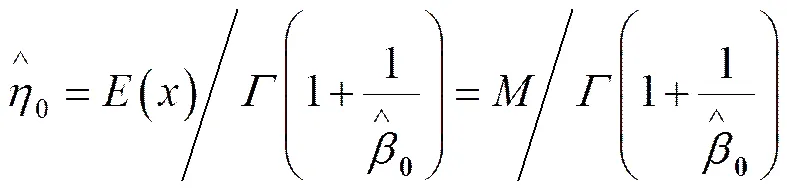
若进行小子样试验，为样本数，利用统计分析可计算出样本均值和方差。

2.2 先验分布

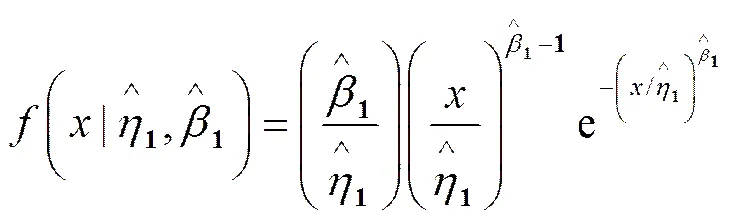
2.3 后验分布

利用贝叶斯估计来推导参数的后验分布，假设0为先验分布，1为后验分布，为似然概率。由贝叶斯分析所得的后验分布也是一个参数为和的威布尔分布。

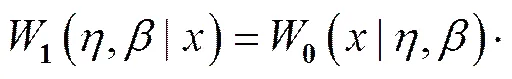
在一系列试验中，一些部件会发生故障，一些会生存下来，此时的失效率遵循二项分布。

(10)

因此，寿命函数的后验分布服从威布尔分布：

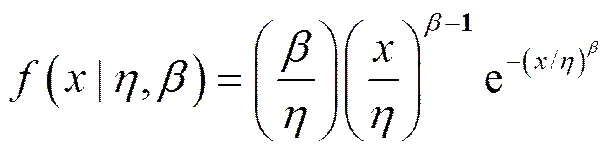
在第一个试验中不需要对参数值进行修正，从第二个开始，试验的先验分布即为最后试验的后验分布。在每一个试验里，可用式(9)—(11)直接计算出后验分布。

2.4 贮存可靠度

如前所述，在每个试验中寿命函数被修正，每个试验中的后验分布即为下一试验的先验分布，导弹贮存可靠度可由式（12）得出：

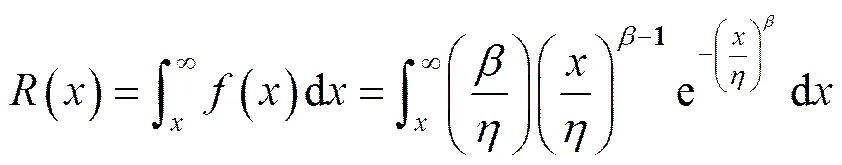
将每个试验的后验分布统计起来，最后可以建立贮存可靠性增长模型。3个试验得出的3种失效率模型如图2所示，可以看出，失效率和失效率方差一步步降低。

3 参数估计

3.1 极大似然估计

参数和的估计值得到之后，部件寿命服从威布尔寿命分布。根据密度函数可得第个试验阶段中第个子试验的第个样本寿命的极大似然函数为：

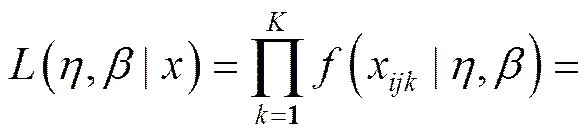
3.2 参数估计修正

针对小子样条件，文献[12]提出了一种Reduces Bias Adjustment(RBA)方法，对寿命参数的估计值进行降偏差修正，并利用蒙特卡罗仿真验证了可用性，而且样本数越大，无偏性越好。

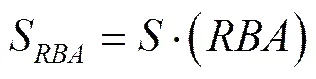
威布尔分布的参数至关重要，决定着样本失效率和方差的大小，为了降低参数值的偏离度，式(14)可变为：

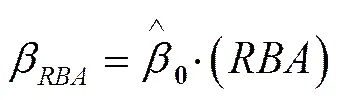
校正后的极大似然函数为：

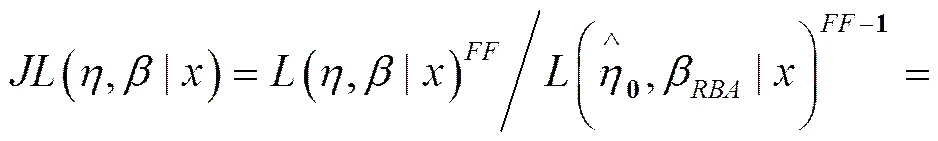
4 实例仿真

以某型导弹发动机为例，进行仿真分析。由于装备试验耗资较大，抽样量一般都比较小。实现小子样加速贮存可靠性建模，反映装备实际情况，是非常必要的。

首先要确定参数和的初始值，由于发动机的样本数很小，值可以适当取高一点。提取5组发生在安全点火装置的故障数据，其贮存时间分别为314，289，357，378，415 h。其寿命服从威布尔分布，进行仿真试验，条件如下。

1）进行5组试验（=5），每组试验包含5个子试验（=5）。

2）5组仿真试验参数和初始值为：(314, 0.9)，(289, 0.86)，(357, 0.75)，(378, 0.56)和(415, 0.2)。

3）5组试验中样本的平均寿命为618.3，827.1，1134.8，1329.3，1780.5 h。

4）当样本的寿命小于试验用时，即将样本视为故障。

5）采取定时截尾试验，5组试验用时为700，700，700，300，5 h。

仿真结果如图3所示，可以看出，可靠性随试验的进行而逐步得到增长。

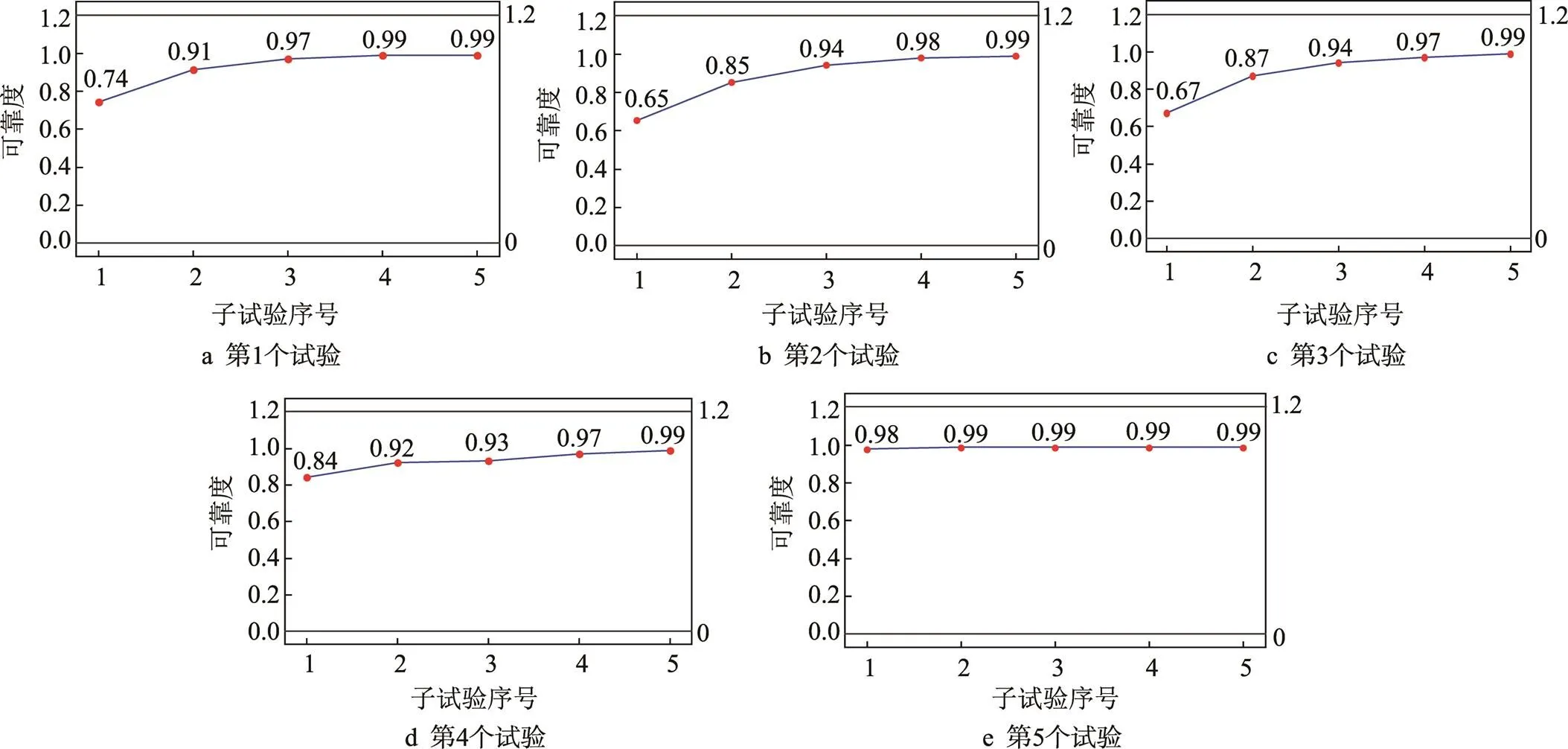
图3 仿真结果

5 结论

1）Bayes算法易行、精度高，该加速贮存试验参数估计方法可有效对导弹贮存可靠性进行评估。

2）算例给出了贮存寿命参数的极大似然估计，利用RBA方法对参数估计值进行降偏修正，得出参数的修正似然估计值。文中给出的参数估计在均方误差意义下结果较优，算法中对寿命参数估计值的修正也很重要。

[1] 张建荣, 孙臣良, 冷江. 海防导弹贮存可靠性研究浅谈[J]. 海军航空工程学院学报, 2004, 19(4): 463-466.

[2] 刘天放, 吴进煌, 刘海波, 等. 导弹贮存可靠性试验中右删失数据的分布选择方法[J]. 四川兵工学报, 2015(1): 91-94.

[3] 洪亮, 胡小国, 崔旭涛. 海军导弹环境适应性试验条件建设方案研究[J]. 装备环境工程, 2012, 9(6): 97-99.

[4] 李久祥. 整机加速贮存寿命试验研究[J]. 质量与可靠性, 2004(4): 14-17.

[5] 陈兵, 李星. 加速寿命试验技术在国内外的工程应用研究[J]. 强度与环境, 2010, 37(6): 31-38.

[6] CHERNOFF H. Optimal Accelerated Life Designs for Estimation[J]. Technometrics, 1962,4(3): 223-235.

[7] MIL-STD-810G, Test Method Standard for Environmental Engineering Considerations and Laboratory Tests Test[S].

[8] 徐廷学, 甄伟, 陈红. 基于Bayes理论的导弹贮存可靠性试验研究[J]. 海军航空工程学院学报, 2006, 21(6): 672-674.

[9] WALLS L, QUIGLEY J. Building Prior Distributions to Support Bayesian Reliability Growth Modeling Using Expert Judgement[J]. Reliability Engineering and System Safety, 2001, 74: 117-128.

[10] KUMAR U D. 可靠性、维修性与后勤保障——寿命周期方法[M]. 刘庆华, 宋宁哲, 译. 北京: 电子工业出版社, 2009.

[11] LAWLESS J F. Statistical Models and Methods for Lifetime Data[M]. New York: John Wiley & Sons, Inc, 1982.

[12] Abemethy R B. An Irish Odyssey Leads to Improved Maximum Likelihood Estimates[M]. WeiiullNEWS, 14 “ Edition. North Palm Beach: Wes Fulton, Torrance, 1999.

Estimation of Parameters for Missile Accelerated Storage Life Tests Based on Bayes Theory

LU Ming-zhang, SONG Yong-jun, ZHAO Hai-jun

(Postdoctoral Programme of PLA, No. 91049 Troop, Qingdao 266102, China)

Objective To study the question of parameter estimation for missile accelerated storage life tests. Methods A series of repeated and continuous accelerated simulation tests for missile storage life were designed with insufficient data. The results of previous test was taken as prior distribution of the next test. An accelerated storage life model of missile was established based on Bayes method to propose the algorithm of estimation of storage life parameters and discuss methods for reliability assessment of missile storage. Results The example provided the maximum likelihood estimation of parameters. The value of estimation was adjusted with RBA method and the storage reliability of missile was proposed. The mean square errors of the new estimation are less. Conclusion Bayes algorithm of sequence tests is simple and precise, which will be applicable to evaluation of missile storage reliability.

missile; storage test; maximum likelihood estimation

10.7643/ issn.1672-9242.2017.08.005

TJ760.6+23

A

1672-9242(2017)08-0025-05

2017-03-21；

2016-04-15

飞行器海上测量与控制联合实验室开放基金资助项目（FOM2014OF15）

卢明章（1959—），男，山东蓬莱人，博士，高级工程师，主要研究方向为固体火箭发动机及寿命可靠性。