动车组运维效率关联规则挖掘优化算法
2017-09-15张春周静
张 春 周 静
(北京交通大学计算机与信息技术学院 北京 100044) (高速铁路网络管理教育部工程研究中心(北京交通大学) 北京 100044)
动车组运维效率关联规则挖掘优化算法
张 春 周 静
(北京交通大学计算机与信息技术学院 北京 100044) (高速铁路网络管理教育部工程研究中心(北京交通大学) 北京 100044)
(chzhang1@bjtu.edu.cn)
随着动车组运营时间和运营里程的增长,动车组运维系统积累了大量的数据.利用高效的关联规则挖掘算法从动车组运维数据中快速发现有用的信息,对于提高动车组关键部件运维效率具有重要意义.针对动车组运维数据的数据量巨大、价值密度低的特点,设计一种基于近似最小完美Hash函数的AMPHP(approximate minimum perfect hashing and pruning)算法,相较于传统的直接Hash和修剪(direct hashing and pruning, DHP)算法,它可以过滤掉所有的非频繁项集,无需额外的数据库扫描.为了突破单机算法的性能限制,借鉴SON算法思想对AMPHP算法进行并行化改进,提出AMPHP-SON算法,进一步提高算法性能.使用实际的动车组牵引电机运维数据进行测试分析,实验结果表明,AMPHP-SON算法具有很好的时间性能,且挖掘出的规则可以有效地指导动车组修程修制优化,从而达到提高动车组运维效率的目的.
关联规则挖掘;DHP算法;近似最小完美Hash函数;SON算法;动车组
在复杂的高速铁路动车组中,对故障部件的维修往往需要多个系统、多个环节、多个部门的协同,不仅涉及故障定位等本身因素,还包括设备、备品备件、人员、工位、维修计划等.因此,为了提高故障维修效率,不仅需要各个装置自身的故障判断规则,同时还需要相关的信息传递及相互影响的规则.而随着动车组运营时间和运营规模的增大,动车组运维系统积累了大量的数据,如何从这些海量数据中快速发现有用的信息成为亟待解决的问题.对于以上的这些需求,利用关联规则挖掘(association rule mining)技术也可以有效地实现.
关联规则挖掘是数据挖掘领域最活跃的研究方法之一,可以用来发现事情之间的联系,在事务数据集中发现频繁项集是一个基础概念.令I={i1,i2,…,im},其中i1,i2,…,im为m个不同的项(item);令T={t1,t2,…,tn}是所有事务的集合,可称为事务数据集(transaction dataset).包含0个或多个项的集合被称为项集(itemset),它的一个重要性质是支持度计数(support count),即包含特定项集的事务个数.支持度(Support)为包含特定项集的事务的个数占整个事务数据集中的比例.满足最小支持度阈值的所有项集被称为频繁项集.
Apriori算法[1]是一种经典的关联规则挖掘算法,但会产生大量的候选集且需要重复扫描数据库,效率低;直接Hash和修剪(direct hashing and pruning, DHP)算法是在Apriori算法的基础上,利用Hash修剪技术改进的算法,它有效减小了候选集大小,在性能上得到了一定的提高.但在面对大数据量的事物数据库时,DHP算法的Hash过滤效果不够好,且时间开销也会随之增大.为了解决上述2个问题,本文提出了相应的解决方案:1)基于近似最小完美Hash函数设计一种新的近似最小完美Hash和修剪(approximate minimum perfect hashing and pruning, AMPHP)算法,可以百分百地过滤出非频繁项集,无需额外地扫描数据库;2)基于SON算法的思想,对AMPHP算法进行并行化改进,提出AMPHP-SON算法,以减少时间开销.
关联规则挖掘最早是为了发现超市交易数据库中不同的商品之间的关系的,现广泛应用于客户关系管理(customer relationship management, CRM)领域[2].而利用快速、高效的数据挖掘算法从动车组的运维数据中挖掘出有效的信息,对于提高动车组运维效率具有重要的意义.因此本文将改进的AMPHP-SON算法应用于动车组运维效率关联规则挖掘,以发现影响动车组关键部件运维效率的重要因素,进而支撑动车组修程修制优化,提高运维效率,降低运维成本.实验证明,本文提出的AMPHP-SON算法具有很好的时间性能,且挖掘出的规则可以有效地指导动车组运用维修.
1 相关工作
1.1 DHP算法
为了解决Apriori算法的效率瓶颈问题,Park等人[3]提出了基于Hash修剪技术的DHP算法.DHP算法使用Hash函数来高效地产生候选项目集,利用Hash表地址对应的计数值删除不是频繁项集的候选项集,这样减少了需要验证的候选项集,特别是解决了生成频繁2-项集时的性能瓶颈问题.DHP算法在寻找k-1-项目集Lk-1时,为候选集Ck生成一个Hash表,并且根据这张Hash表来过滤候选集Ck.在生成Hash表的时候无法避免冲突的产生,因此DHP算法设置了散列桶(桶中只存储Hash到该桶中的元素个数,并不存储元素本身),将产生冲突的候选项集放入桶中并增加对应的桶计数.但当项目个数较多或者事物集较大时,大部分桶计数都将会达到预设的最小支持度计数,对候选集的过滤效果不够好,且为了判断这些桶中的候选集是否为频繁项集,还需再次扫描数据库.这种情况下DHP算法的性能可能还不如Apriori算法好.
为了解决上述DHP算法压缩效果不好,还需再次扫描数据库的问题,Tseng等人[4]提出了多阶段索引和修剪(multi-phase indexing and pruning, MPIP)算法[5].MPIP算法的主要贡献是使用最小完美Hash函数解决了DHP算法中的Hash冲突问题,它可以为每一个项目集产生唯一的Hash地址,并在不浪费空间的情况下将它们映射到Hash表中,也即Hash表的长度等于所有项目集的个数.Hash表的每一项都是该地址所对应的项目集的支持度,因此可以用来过滤候选项集并直接给出频繁项集,可以避免重复扫描数据库,从而减少对磁盘IO的访问.“最小完美Hash函数”[6]在概念上很完美,生成的思想也很不错,但在动车组的大数据应用环境中却并不合适,因为当数据集很大时,生成最小完美Hash函数的开销也会非常大.吴恒等人提出另一种基于动态链改进的DLDHP算法[7],他们使用链接技术解决Hash冲突问题,但链接技术需要使用额外的数据结构,节点中同时存储元素本身、元素计数和指针域,浪费内存空间;并且在Hash函数设计不当时,Hash表会退化成链表,其查找效率非常低.
1.2 SON算法
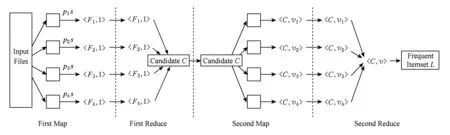
SON算法是基于作者Savasere,Omiecinski,Navathe的名字而命名的[8],它能够在2次扫描的代价下去掉所有的伪反例和伪正例[9].其基本思路是,将输入文件分成多个组块,将每个组块看成是一个样本数据,然后在该组块上运行任一种关联规则算法.如果每个组块占整个文件的比例为p,而s是支持度阈值,可以使用ps作为支持度阈值,发现每个组块上的频繁项集,这是第1次扫描.一旦所有的组块都采用了上述方法进行了处理,就可以将所有在一个或多个组块上发现的频繁项集进行合并,这些项集为候选项集.如果某个项集在任意组块上都不频繁,那么它在每个组块上的支持度都低于ps,由于组块的数目是1p,因此该项集在所有数据集上的支持度将低于(1p)ps=s.所以,在所有数据集上频繁的项集至少会在一个组块上是频繁的.第2次扫描中对所有候选项集计数并选出支持度不低于s的频繁项集.
2 基于近似最小完美Hash函数的AMPHP算法
2.1 近似最小完美Hash函数
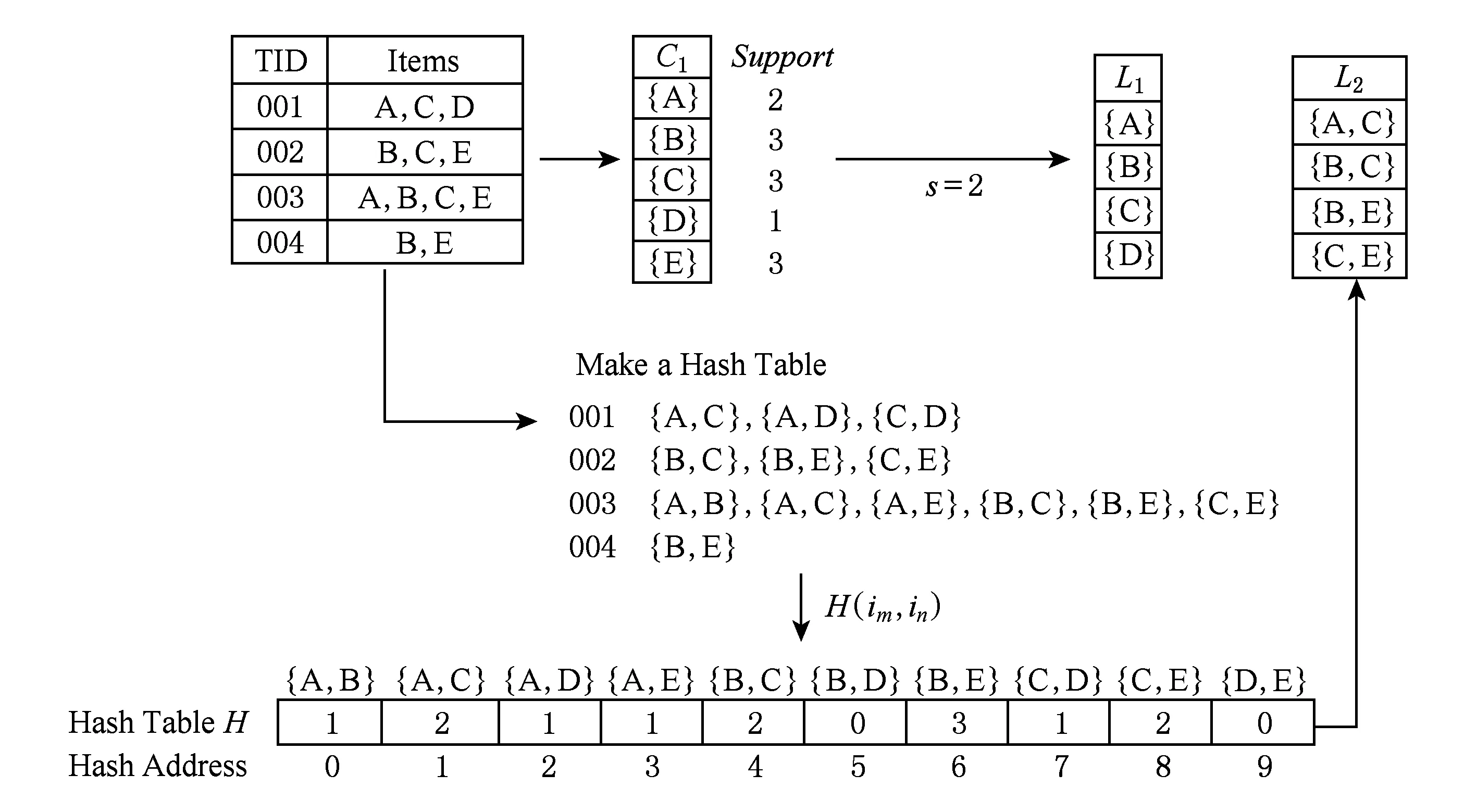
为了解决DHP算法中的Hash冲突问题,也避免MPIP算法中生成最小完美Hash函数的巨大开销,本文提出一种近似最小完美Hash函数(approximate minimum perfect hashing function)来代替,并最终提出AMPHP算法.近似最小完美Hash函数不会产生Hash冲突,且所用空间即Hash表的长度也接近事物数据库中不重复项集的个数.
I={i1,i2,…,im}为全集,按序编号分别为1,2,…,m,对于给定的2项组合,给出Hash函数:
H({im,in})=S(m-1)+n-1-m(m+1)2,
(1)
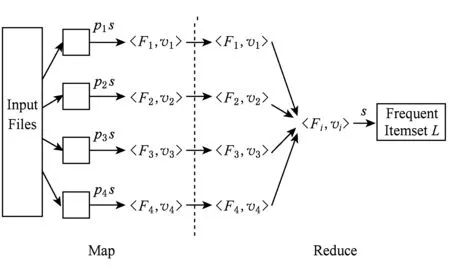
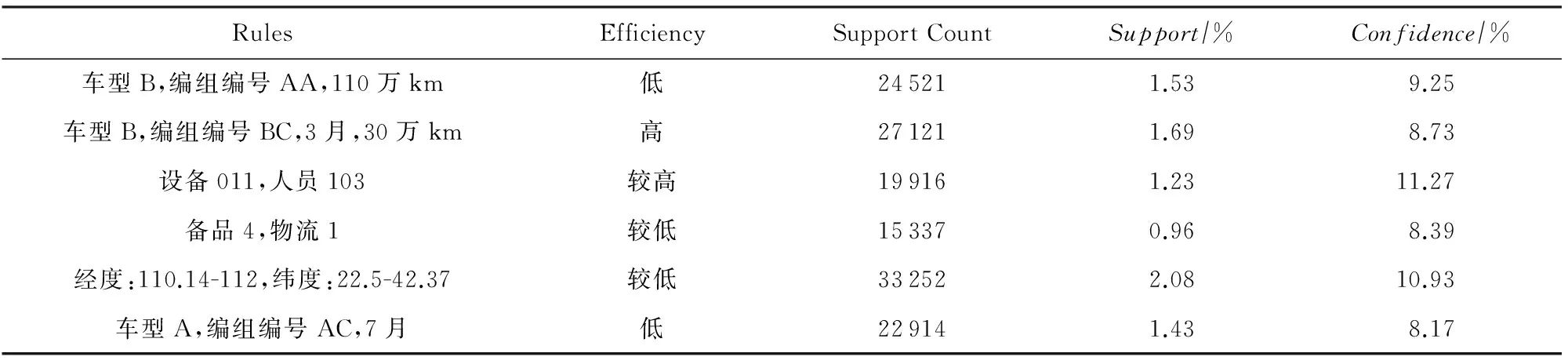
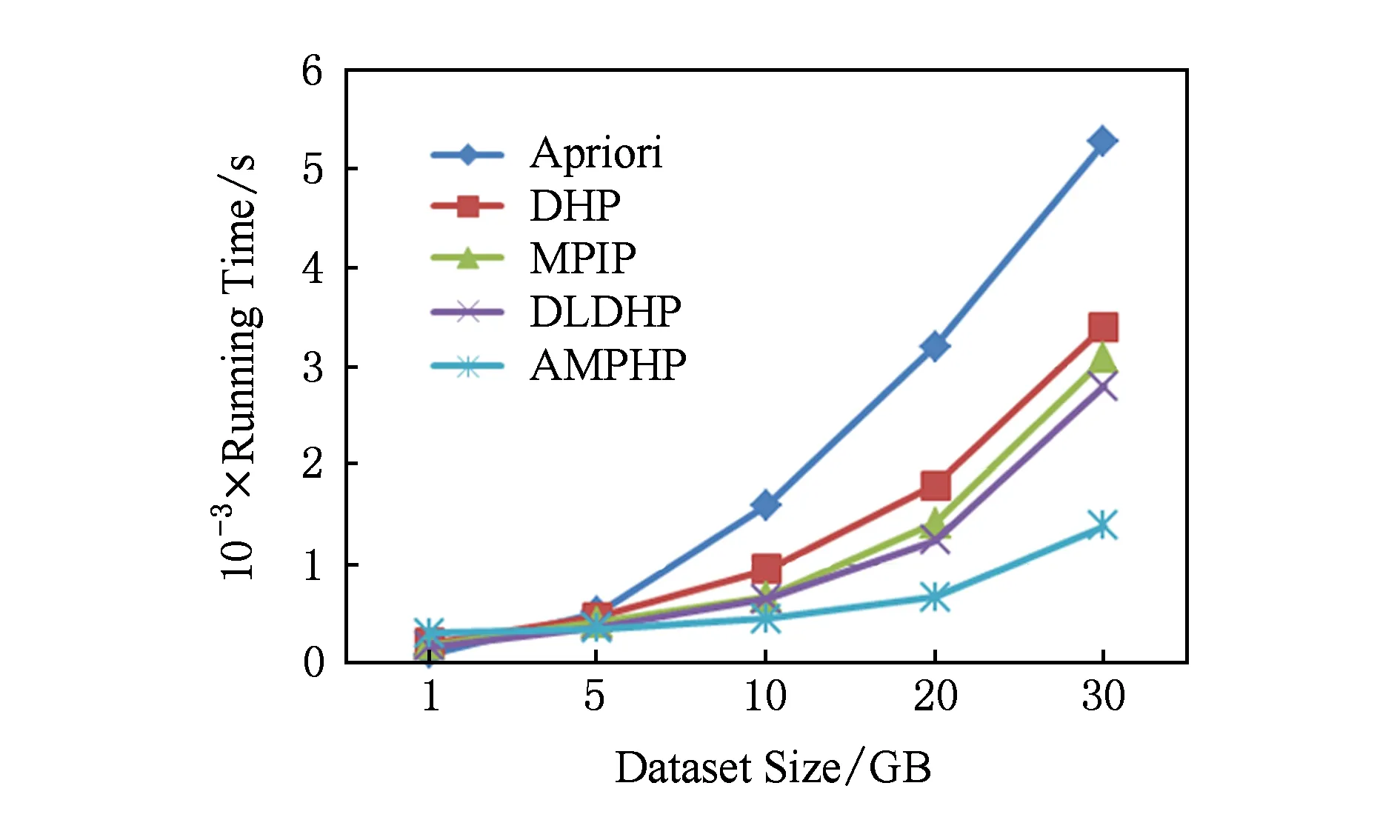
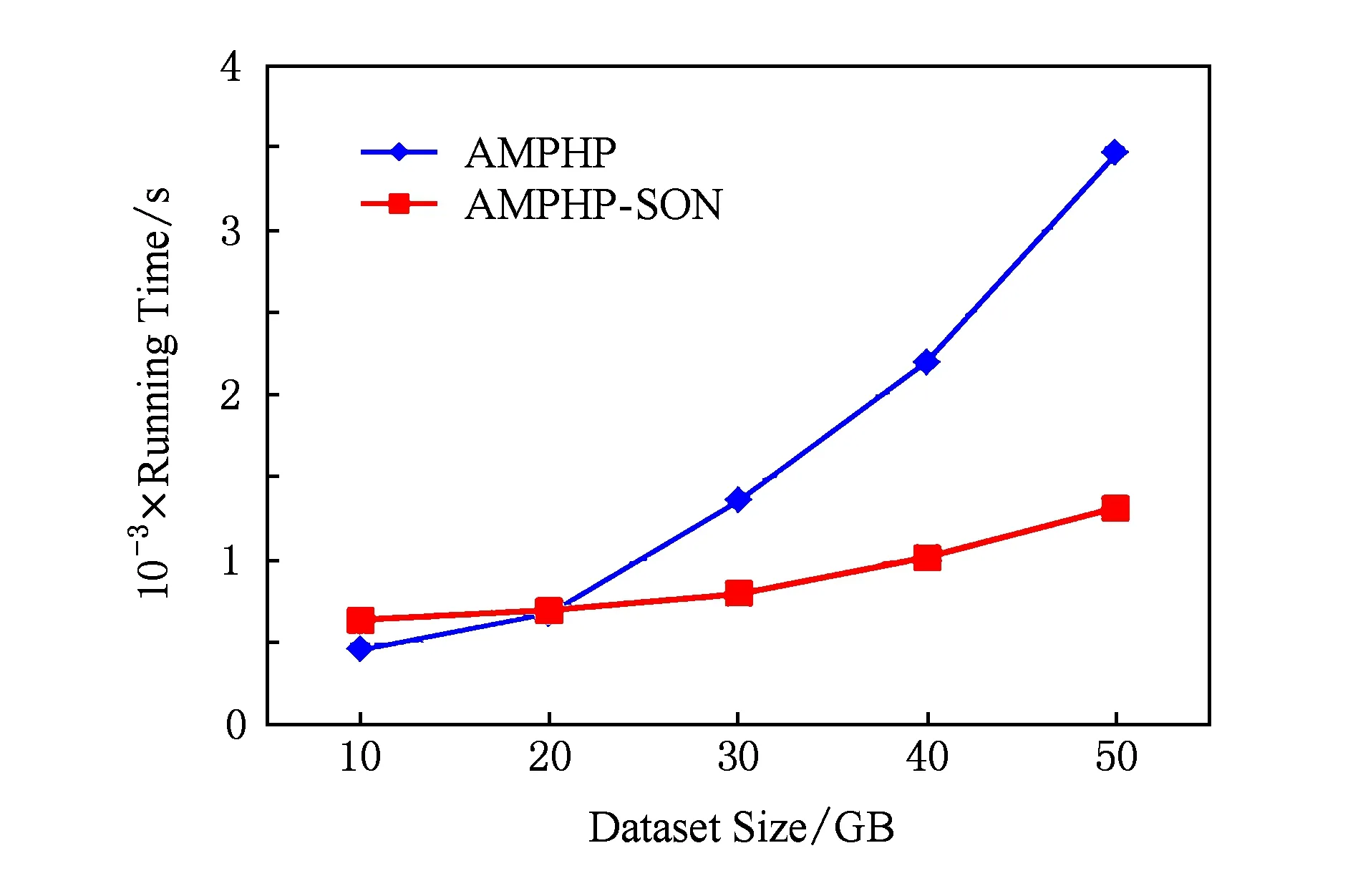
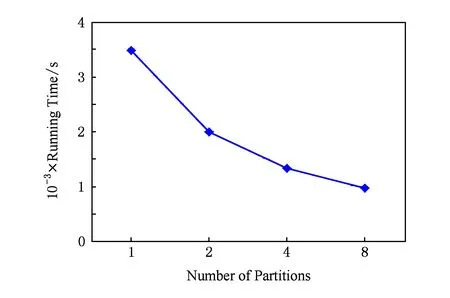
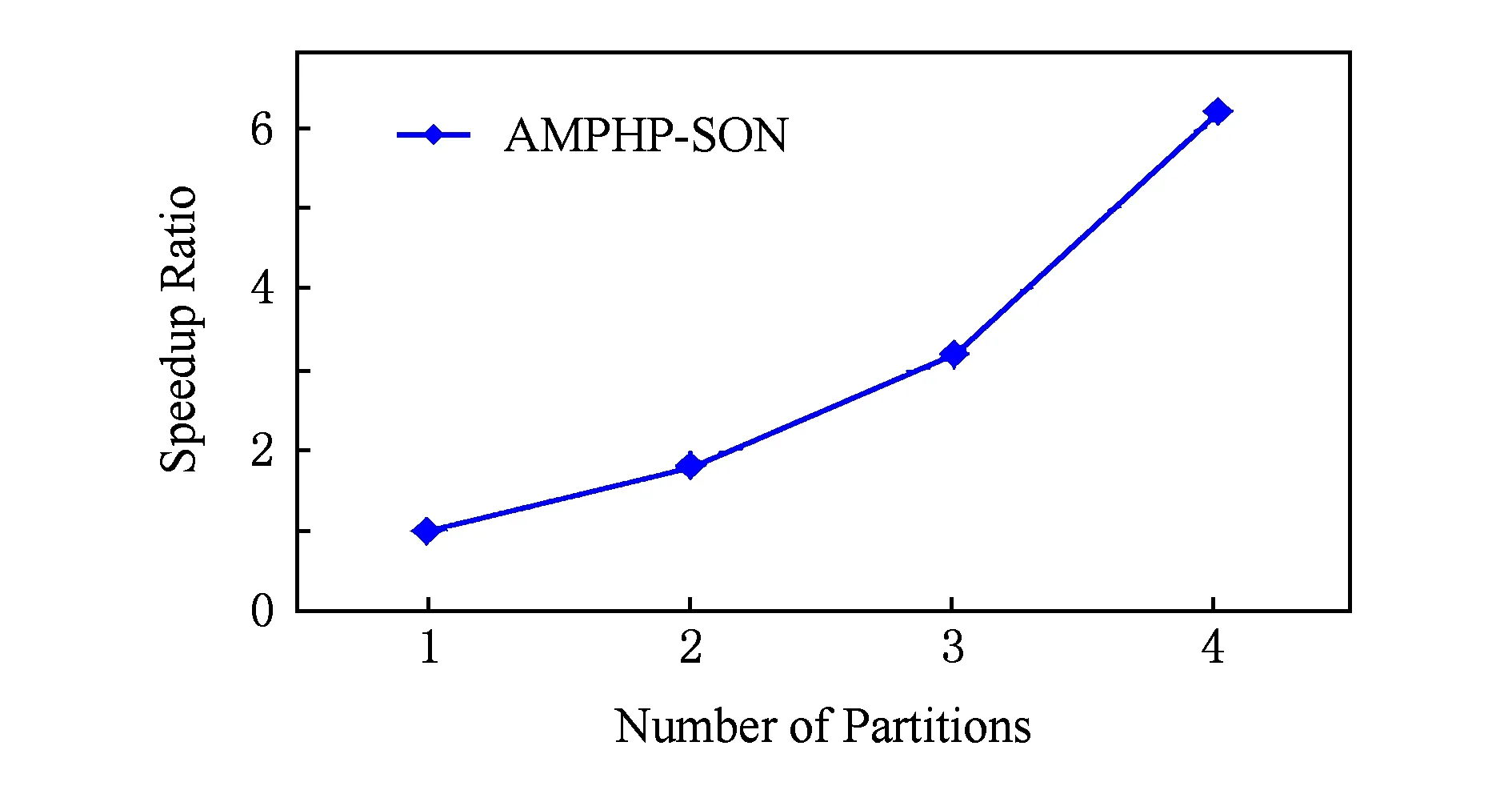
其中,S为事物数据库中项的总数加1;m和n为自然数,分别为im,in的编号,且m 以下证明任意2个不同的2-项集不会映射到Hash表的同一个单元中,即不会产生冲突. 命题1. 若H({im1,in1})=H({im2,in2}),则必须m1=m2且n1=n2. 证明. 假设存在m1≠m2,n1≠n2,使得H({im1,in1})=H({im2,in2})成立. 令G=H({im1,in1})-H({im2,in2})=S(m1-1)+n1-1-m1(m1+1)2-[S(m2-1)+n2-1-m2(m2+1)2]=(m2-m1)(1+m2+m1-2S)2+(n1-n2). 1)m1=m2,n1≠n2. G=(m2-m1)(1+m2+m1-2S)2+(n1-n2)=n1-n2≠0. 2)m1≠m2,n1=n2. G=(m2-m1)(1+m2+m1-2S)2+(n1-n2)=(m2-m1)(1+m2+m1-2S)2. 因为m1≠m2,所以m2-m1≠0;因为m1 3)m1≠m2且n1≠n2. 假设m1 ① 若m2-m1=1,则m2=S-x-a+1. 所以n2=n1+[1+(S-x-a+1)+(S-x-a)-2S]2=n1-x-a+1. 又n1=S-x,所以n2=S-2x-a+1. 又m2=S-x-a+1,所以n2 ② 若m2-m1>1,则n2≤n1+1+S-x-a+m2-2S=S-x+1+S-x-a+m2-2S=m2-2x-a+1. 又x,a均为自然数,a>0,所以n2≤m2,与已知矛盾. 同理,当m1>m2时,可得相同结论.故,必须m1=m2且n1=n2时,H({im1,in1})=H({im2,in2})才成立. 证毕. 因此对于给定的Hash函数H({im,in})=S(m-1)+n-1-m(m+1)2,任意2个不同的2-项集不会映射到Hash表的同一个单元中,即不会产生冲突.在扫描事物数据库中的每条交易产生L1的同时,对每条交易的所有2项组合作一个Hash计数,对2-项集{im,in}进行计数时,就将Hash表对应位置中的计数值加1.当扫描事物数据库完成以后,不但得到L1而且还得到一个Hash表H,H当中的每个单元的值是一个计数累加.判断该单元中计数值是否大于等于支持度阈值,如果是,则这2项组合为L2中的一员,否则就不是L2中的成员. 2.2 AMPHP算法 我们采用表1所示的事物数据库来举例说明AMPHP算法的流程.项A,B,C,D,E的序号分别为1,2,3,4,5,对于给定的Hash函数H({im,in})=S(m-1)+n-1-m(m+1)2,其中S=5,对该事物数据库中每条交易的所有2项组合作Hash计数: Table 1 Transaction Database 例如,对于二项集{A,C},A,C的序号分别为1和3,则H({i1,i3})=5×(1-1)+3-1-(1+1)2=1,即{A,C}映射到Hash表地址1所对应的单元中,将Hash表地址1所对应的单元中的计数值加1.具体的Hash过程如图1所示: Fig. 1 Hash process of AMPHP algorithm图1 AMPHP算法的Hash过程 如图1所示,AMPHP算法采用近似最小完美Hash函数,在生成L1扫描事物数据库的同时,有效地将每一个2-项集映射到Hash表唯一的地址中进行计数,通过将计数值与预设的支持度阈值s进行比较,从而可以过滤掉所有的非频繁2-项集.从图1可以看出,AMPHP算法在1次数据库扫描中可以同时得到L1和L2,在第1次和第2次迭代中不会产生候选项集,具有很好的空间和时间性能. 3.1 AMPHP-SON算法思想 AMPHP算法虽然本身已经具有很好的时间和空间性能,但基于单机处理的数据挖掘只能处理简单、小规模的数据集.而随着动车组运维数据的积累,事物数据库不断增大,单机性能已无法满足在大数据集中快速发现有用规则的需求.因此本文借鉴SON算法的思想,对AMPHP算法进行并行化改进[10],最终提出AMPHP-SON算法. Fig. 2 Flow of SON algorithm图2 SON算法流程 SON算法非常适合于并行计算环境.每个组块可以并行处理,它们产生的频繁项集合并成候选项集.将所有候选项集分布到多个处理器上进行处理,每个处理器计算每个候选项集在1个组块上的支持度,最后对它们求和得到每个候选项集在整个数据集上的支持度.上述过程可以很自然地使用2轮MapReduce迭代实现[11],如图2所示,其中pi为每个Map任务所得到输入文件占总输入文件的比例,Fi为满足本Map任务支持度阈值的项集,vi为候选集在本Map任务所分配数据集上的支持度,s为支持度阈值.从图2可以看出,SON算法第1轮迭代求出局部频繁项集,第2轮迭代求出全局频繁项集[12].但其缺点是仍需要2次扫描数据库,而扫描数据库进行磁盘IO会占用大量的时间. 为了减少扫描数据库的次数,在SON算法的第1次扫描数据库中使用AMPHP算法,直接计算每个项集在各自组块上的计数值,然后在Reduce阶段统计每个项集在整个数据集上的支持度,通过与预设的支持度阈值进行比较,得出频繁项集.具体过程如图3所示,其中pi为每个Map任务所得到输入文件占总输入文件的比例,Fi为满足本Map任务支持度阈值的项集,vi为候选集在本Map任务所分配数据集上的支持度,s为支持度阈值. Fig. 3 Flow of AMPHP-SON algorithm图3 AMPHP-SON算法流程 3.2 AMPHP-SON算法实现 本文提出的AMPHP-SON算法是基于AMPHP算法的分区算法,它只需要1轮MapReduce迭代即可找出频繁项集.Map阶段和Reduce阶段的具体任务和关键代码如下所述. 1) Map阶段 Map阶段,该阶段每个Map任务完成从事物数据集的某一个分区中读取到事务,并将该分区中所有的事务存储在本地内存中,然后利用AMPHP算法算出本分区的局部频繁项集,最后输出的是一个键值对〈Fi,vi〉,其中Fi是本分区的一个局部频繁项集,vi是该局部频繁项集在本分区的支持度.以下为Mapper类的部分关键代码: Class Mapper{ ListtSet; MaplocalFI; map(key,value){ transaction=genTransaction(value); tSet.add(transaction); } cleanup(){ localFI=genFrequentItemsets(transaction); for(inti=1;(fis=localFI.get(i))≠null;i++) for(f:fis) write(f,v); } genFrequentItemsets(transaction){ L1=find(transaction,minsupport); for(intk=2;Lk≠∅;k++){ Ck=Apriori_gen(Lk-1); Lk=AMPHP_Hash(Dk); Dk+1=pruning(Dk); } }} 2) Reduce阶段 Reduce阶段,该阶段的每个Reduce任务会处理1组局部频繁项集,上个阶段所有的Map任务输出的相同局部频繁项集会集中到同一个Reduce任务上进行处理,Reduce任务就是合并计算该局部频繁项集在整个数据集上的支持度,将其支持度与支持度阈值相比较,最终得出全局频繁项集.Reducer类的部分关键代码如下: Class Reducer{ reduce(key,value){ write(f,v); } } 4.1 应用环境 整个实验是在Hadoop平台下运行的,采用了Hadoop的1.0.4稳定版本.硬件设备为9台x86架构的PC,其中1台是Master节点,其余8台是Slave节点.主设备节点采用Intel至强处理器,内存为2 GB;从设备节点采用了AMD 4核处理器,主频为2.7 GHz,内存为2 GB. 4.2 数据准备 本实验数据的来源是国内某动车组运用检修段2012—2014年的所有动车组牵引电机检修数据.经过缺省值处理、归一化、离散化[13]等一系列数据预处理操作之后,选取50 GB大小的数据集. 4.3 结果分析 在上述实验环境和实验数据的基础上,应用本文提出的AMPHP-SON算法对动车组牵引电机运维数据进行关联规则挖掘,得出的动车组运维效率关联规则部分结果如表2所示: Table 2 Partial Results of the Association Rules of EMU Operation and Maintenance Efficiency 如表2所示,规则“车型B,编组编号AA,110万km=>低[Support=1.53%,Confidence=9.25%]”的含义是车型B编组编号AA的动车组,在运行累计里程达110万km时,运维效率低,支持度为1.53%,置信度为9.25%.该规则符合实际意义,即临近大修时牵引电机易出现故障,且故障原因较复杂,因此检修过程慢,运维效率低.规则“设备011,人员103=>较高[Support=1.23%,Confidence=11.27%]”的含义是人员103使用设备011对牵引电机进行检修,运维效率较高,支持度为1.23%,置信度为11.27%.根据该规则我们可以推测设备011的检修性能较好,人员103检修专业技能较强,利用该规则我们可以合理安排人员和设备,从而达到提高运维效率的目的.规则“经度:110.14—112,纬度:22.5—42.37=>较低[Support=2.08%,Confidence=10.93%]”的含义是在经度为110.14—112且纬度为22.5—42.37的地域内,牵引电机的运维效率较低.从该规则可以初步预测该地域内环境比较恶劣,牵引电机容易发生故障,从而导致维修次数增加,备品备件不足,因此运维效率较低.规则“车型A,编组编号AC,7月=>低[Support=1.43%,Confidence=8.17%]”的含义是车型A编组编号AC的动车组在7月份牵引电机的维修效率低.该规则符合实际意义,即7月份温度较高导致牵引电机故障频发,引起维修次数增加,备品备件不足,从而运维效率低.上两条规则给我们的指导意义是根据不同的地域和时间合理制定备品备件的订购计划,以达到提高运维效率的目的. 4.4 性能分析 为了评估本文所提出算法的性能,我们首先将单机版的AMPHP算法与传统的Apriori算法、DHP算法以及他人改进的MPIP算法、DLDHP算法进行比较,实验数据集的大小分别为1 GB,5 GB,10 GB,20 GB,30 GB,实验结果如图4所示: Fig. 4 Performance comparison of five algorithms图4 5种算法性能比较 Fig. 5 Performance comparison of AMPHP and AMPHP-SON algorithm图5 AMPHP算法与AMPHP-SON算法性能比较 图4显示,在数据集较小的情况下,传统的Apriori算法和DHP算法的性能优于AMPHP算法,因为数据集较小,产生的候选项集也小,对候选项集的判断不会耗费太多时间,但是近似最小完美Hash函数的生成和Hash表的构建都需要耗费额外的时间;在数据集较大的情况下,产生的候选项集也随之增大,AMPHP算法使用近似最小完美Hash函数构建Hash表有效地过滤掉所有的非频繁项集,节省了再次扫描数据库的时间,因而性能较好. 为了对单机串行的AMPHP算法和多机并行AMPHP-SON算法进行比较,实验数据集的大小分别为10 GB,20 GB,30 GB,40 GB,50 GB,并行AMPHP-SON算法的分区数为4,实验结果如图5所示: 图5显示,在数据集较小的情况下,单机串行的AMPHP算法的性能优于多机并行AMPHP-SON算法,因为此时Hadoop平台自身消耗的时间将远远超过数据处理的时间;在数据集较大的情况下,Hadoop集群用于数据处理的时间将会远远大于集群自身所耗费的时间,并行的AMPHP-SON算法将任务分配给多个节点同时进行处理,其性能优于串行的AMPHP算法. 为了测试分区数对AMPHP-SON算法性能的影响,我们在将50 GB的数据集分成1块、2块、4块、8块的情况下分别运行AMPHP-SON算法,运行结果如图6所示: Fig. 6 Performance of AMPHP-SON algorithm under different partitions图6 不同分区数下AMPHP-SON算法性能 图6显示了随着数据集划分块数的增加,AMPHP-SON算法的运行能够得到接近线性的加速比,如图7所示: Fig. 7 Speedup ratio of AMPHP-SON algorithm图7 AMPHP-SON算法的加速比 本文提出的AMPHP-SON算法,使用近似最小完美Hash函数过滤掉所有的非频繁项集,且借鉴SON算法将关联规则挖掘任务分配给多个节点共同完成,可以快速地从动车组海量运维数据中挖掘出有用的信息,以指导动车组修程修制优化,提高动车组运维效率. [1]Agrawal R. Mining association rules between sets of items in large databases[J]. ACM SIGMOD Record, 1993, 22(2): 207-216 [2]Linoff G S, Berry M J A. Data Mining Techniques: For Marketing, Sales, and Customer Relationship Management[M]. Hoboken, NJ: Wiley Publishing, 2011: 54-55 [3]Park J S, Chen M S, Yu P S. An effective Hash-based algorithm for mining association rules[J]. ACM SIGMOD Record, 2010, 24(2): 175-186 [4]Tseng J C R, Hwang G J, Tsai W F. A minimal perfect hashing scheme to mining association rules from frequently updated data[J]. Journal of the Chinese Institute of Engineers, 2006, 29(3): 391-401 [5]Chiou C K, Tseng J C R. An incremental mining algorithm for association rules based on minimal perfect hashing and pruning[C]Proc of Int Conf on Web Technologies and Applications. Berlin: Springer, 2012: 106-113 [6]Witten I H, Moffat A, Bell T C. Managing Gigabytes: Compressing and Indexing Documents and Images[M]. 2nd ed. San Francisco, CA: Morgan Kaufmann, 1999 [7]Wu Heng, Wu Genxiu, Mao Linchuan, et al. An algorithm for mining association rules of dynamic chain address based on DHP[J]. Journal of Jiangxi Normal University: Natural Science Edition, 2015(5): 463-468 (in Chinese)(吴恒, 吴根秀, 毛临川, 等. 一种基于DHP的动态链地址关联规则挖掘算法[J]. 江西师范大学学报: 自然科学版, 2015(5): 463-468) [8]Savasere A, Omiecinski E, Navathe S B. An efficient algorithm for mining association rules in large databases[C]Proc of Int Conf on Very Large Data Bases. San Francisco, CA: Morgan Kaufmann, 1995: 432-444 [9]Rajaraman A, Ullman J D. Mining of Massive Datasets[M]. Cambridge, UK: Cambridge University Press, 2012 [10]Xiao Tao, Yuan Chunfeng, Huang Yihua. PSON: A parallelized SON algorithm with MapReduce for mining frequent sets[C]Proc of the 4th Int Symp on Parallel Architectures, Algorithms and Programming. Los Alamitos, CA: IEEE Computer Society, 2011: 252-257 [11]Guo Jinwei, Pi Jianyong. Implementation of SON algorithm based on MapReduce[J]. Journal of Computer Applications, 2014, 34(S1): 100-102 (in Chinese)(郭进伟, 皮建勇. 基于MapReduce的SON算法实现[J]. 计算机应用, 2014, 34(S1): 100-102) [12]Xu Hui, Sun Qi, Yang Lin, et al. Parallel algorithm design for mining association rules based on big data[J]. Computer Science, 2014, 10(41): 434-437 (in Chinese)(徐慧, 孙琪, 杨林, 等. 面向大数据的关联规则挖掘算法并行化设计[J]. 计算机科学, 2014, 10(41): 434-437) [13]Hu Hui. Research and implementation of mining association rules for EMU failure data based on Hadoop[D]. Beijing: Beijing Jiaotong University, 2015: 21-22 (in Chinese)(胡辉. 基于Hadoop的动车组故障数据关联规则挖掘研究与实现[D]. 北京: 北京交通大学, 2015: 21-22) Zhang Chun, born in 1966. Master. Senior engineer. Her main research interests include big data, data mining and modern railway information technology. Zhou Jing, born in 1992. Master. Her main research interests include big data, data mining and modern railway information technology. Optimization Algorithm of Association Rule Mining for EMU Operation and Maintenance Efficiency Zhang Chun and Zhou Jing (SchoolofComputerandInformationTechnology,BeijingJiaotongUniversity,Beijing100044) (EngineeringResearchCenterofNetworkManagementTechnologyforHighSpeedRailway(BeijingJiaotongUniversity),MinistryofEducation,Beijing100044) With the increase of EMU operation time and mileage, EMU operation and maintenance system has accumulated a large amount of data. Using the high-performance association rule mining algorithms to quickly find useful information from the EMU operation and maintenance data, is of significant importance for improving the operation and maintenance efficiency of the key components of the EMU. In the view of the characteristics of EMU operation and maintenance data—huge volume and low value density, we design the AMPHP algorithm based on the approximate minimal perfect Hash function. Compared with the traditional DHP algorithm, it can filter out all the infrequent item sets without additional database scanning. In order to break the limitation of the single machine algorithm and further improve the performance of the algorithm, we use the idea of SON algorithm for reference to parallelize the AMPHP algorithm and finally propose the AMPHP-SON algorithm. Some experiments have been performed on the operation and maintenance data of EMU traction motor. The experimental result shows that the AMPHP-SON algorithm has good time performance and the rules dug out can be effectively used to guide the optimization of the repair class and repair system of EMU, so as to improve the efficiency of EMU operation and maintenance. association rules mining; DHP (direct hashing and pruning) algorithm; approximate minimum perfect Hash function; SON algorithm; EMU 2016-07-05; 2017-02-22 国家“八六三”高技术研究发展计划基金项目(2015AA043701) This work was supported by the National High Technology Research and Development Program of China (863 Program)(2015AA043701). 周静(14120456@bjtu.edu.cn) TP311
3 AMPHP-SON算法
4 动车组运维效率关联关系分析
5 结束语


