支持社会协同计算的跨组织工作流任务分派算法

孙 勇 谭文安,2

1(南京航空航天大学计算机科学与技术学院 南京 211106)2 (上海第二工业大学计算机与信息工程学院 上海 201209)

支持社会协同计算的跨组织工作流任务分派算法

孙 勇1谭文安1,2

1(南京航空航天大学计算机科学与技术学院 南京 211106)2(上海第二工业大学计算机与信息工程学院 上海 201209)

(syong@nuaa.edu.cn)

针对社会协同计算带来的不可靠性和社会网络所固有的大规模性问题，提出了支持社会协同计算的跨组织工作流任务分派优化算法.首先，采用了基于工作流任务子网分层的优化模型，将复杂社会网络图进行有效地划分，从而简化了社会网络成员的协作关系评估问题；然后，根据划分后网络的拓扑特征，设计了一种基于工作流任务子网连接点的快速介数中心性计算方法，以高效地选取跨组织业务项目的领导者；最后，采用基于任务子网划分的最短路径近似算法，实现了快速查找跨组织业务过程的协作成员；并且，理论证明了支持社会协同计算的工作流分派算法的可行性.实验结果表明所提算法大幅降低了社会协同计算的复杂性，保证了较高的准确性，解决了工作流任务成员之间的关系评价和人工团队组合优化的时效性问题，为社会协同计算的任务分派提供了一种新的思路.

协同计算；团队组合；任务分派；跨组织工作流；社会网络

完全自动执行的业务过程难以满足所有实际社会协同计算应用的需求，复杂的社会协同计算系统中某些任务活动必须借助跨组织的专业人工服务才能圆满完成[1-2].因此，为有效地解决机器难以实现的复杂问题，社会协同计算系统采用WS-BPEL工作流技术，通过将人工任务外包给专家社会网络服务，实现社会成员之间的协同计算.在WS-BPEL工作流应用中，专家任务被定义为WS-BPEL工作流控制结构中的一个活动，社会协同计算系统通过调用专家服务解决跨组织业务中人工任务的执行问题，从而实现专家服务与业务过程之间的松散融合[1-2]，如图1所示：

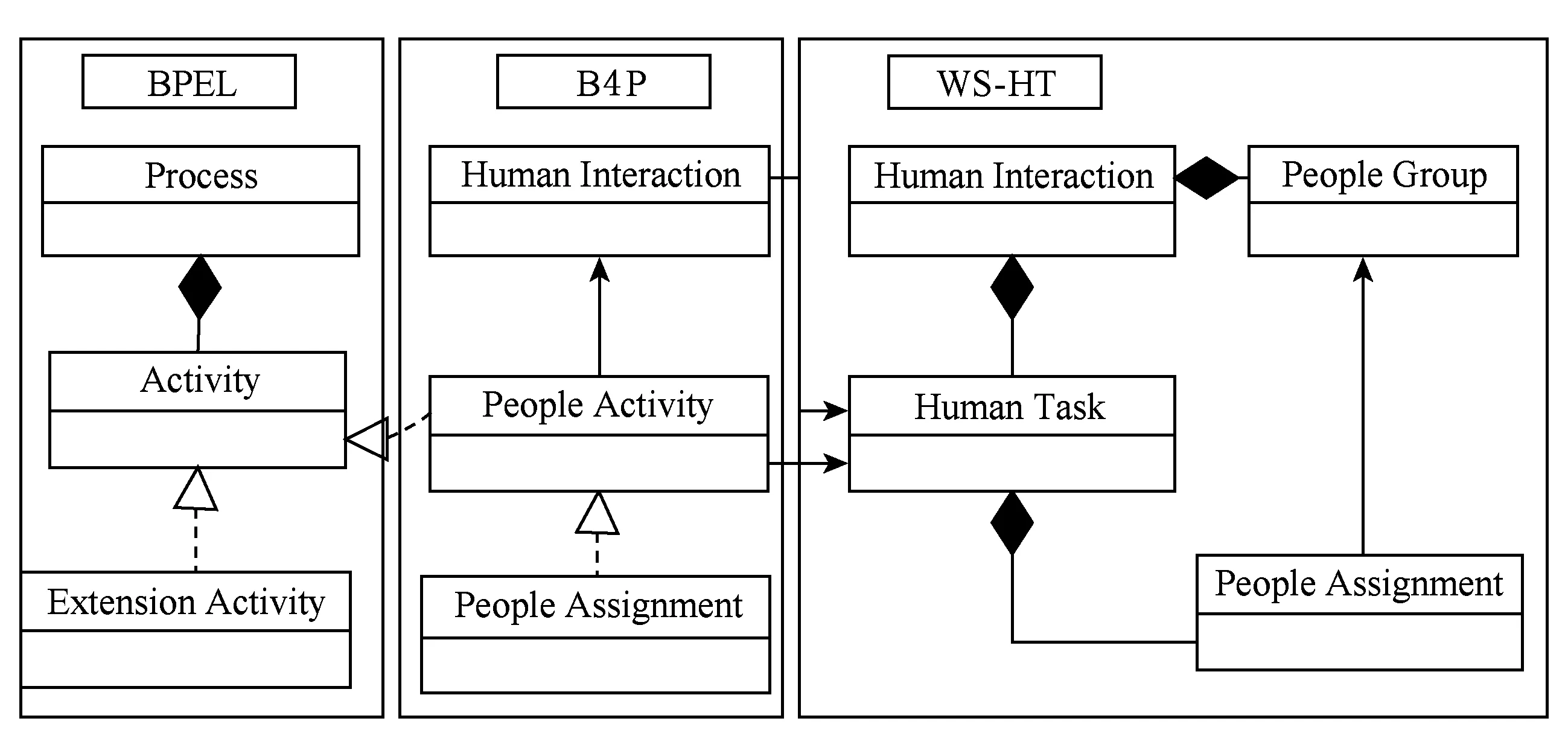
Fig. 1 Cross organizational workflow model based on expert services[2]图1 基于人工服务的跨组织工作流应用模型[2]

面向专家社会化网络的协同计算模式从企业内部成员交互演变为跨组织之间的协作，导致组织模型呈现出动态性和不稳定性.跨组织工作流系统采用质量管理过程技术，实现跨组织业务质量的持续改进，为社会协同计算应用提供了有效的计算机技术支持.面向社会化网络的工作流活动执行前需要分配人工任务，即在工作流任务和专家社会网络之间建立映射关系，跨组织业务的任务分派问题已被证明是NP-hard问题.近年来，工作流任务分派模型构建及其算法优化成为了社会协同计算研究领域的难点和热点问题[2-5]，例如，基于社会化网络的众包计算[3-5]和面向专家社会网络的团队组合发现[6-8].研究者通过探索社会科学知识、理论和方法学，借助基于服务的跨组织工作流技术，有效地促进了面向社会网络的协同计算应用[9].

复杂的社会协同计算项目需要多个跨组织成员共同完成，跨组织工作流的任务分派问题是社会协同计算的最基本难点问题.其中，跨组织成员之间的协同工作效率，不仅依赖于参与者的业务执行者能力，还取决于参与者之间的合作关系.执行跨组织业务的专家成员之间的社会关系直接影响着项目进度，和睦的社会关系有利于跨组织业务项目顺利地进行.在此背景下，社会网络中成员之间的关系评估分析变得十分重要.而且，高效地执行跨组织业务项目要求选择出项目领导者，以协调好不同组织成员之间的关系，并管理好跨组织项目的进度.因此，支持社会协同计算的工作流任务分派模型的首要任务是在大规模社会网络中确立跨组织业务应用的中心领导者，以管理跨组织业务项目的执行；然后，为领导者选取合适的项目协作成员，协同完成工作流任务.为确保跨组织业务项目的顺利进行，领导者必须和每个任务协作成员之间具有良好密切的关系，即项目领导者到任务协作成员之间的最短路径距离尽可能小.

社会协同分析算法采用图数据结构来描述社会网络，通过调用图的算法，分析社会成员之间的协同工作等复杂计算问题.社会成员之间的关系评测依赖于社会成员节点之间的最短路径计算[10-12].然而，社会网络所固有的大规模性、急剧扩张性以及复杂性等特点，给社会网络成员的关系评测算法带来了严峻的挑战.经典的Dijkstra和A*最短路径算法具有很高的复杂度，不适用于规模较大的现实社会网络[10-12].近年来，研究人员提出很多面向大规模社会网络的最短路径优化近似算法，普遍采用了基于参考点的计算方法，通过预先计算生成的辅助数据，提高了后续算法的执行效率.然而，参考点的选择算法是NP-hard问题[9]，其选取结果直接影响着最短距离计算的正确性和效率.而且，从复杂社会网络中查找跨组织项目的领导者是一个难点问题，研究者采用了基于介数中心性的领导者节点确定方法[7]，因为具有高介数中心性的候选领导者节点，总是在多数社会成员节点之间的最短路径上，因此，提高了所选工作流任务成员与领导者的高效协同工作的可能性.但是，目前最高效的介数中心计算方法在无权网络中的算法时间复杂度为O(m×n)，而在加权网络中的时间复杂度为O(m×n+n2×logn)[7-8]，当面向大规模社会网络选取领导者时，同样需要耗费大量的计算成本，其效率不高.

针对社会网络所固有的数据大规模性问题，本文采用了基于工作流任务子网分层的优化模型，将复杂社会网络图进行有效地划分，在此基础上，提出了支持社会协同计算的跨组织工作流分派模型及其高效算法.本文的主要贡献如下：

1) 基于工作流任务划分的人工服务社会网络设计了一种适用于工作流任务子网划分的参考点选择策略；

2) 综合考虑划分后社会网络的拓扑特征，提出了基于工作流任务子网划分的最短路径近似计算方法，其中包括面向任务子网内部和不同任务子网之间的社会成员关系评测算法；创新性地提出了基于任务子网连接点的快速介数中性计算方法，该方法能够高效率地优选出项目领导者；

3) 理论证明了所提出的社会协同计算方法的可行性;

4) 使用真实数据集仿真验证分析了支持复杂社会协同计算的跨组织工作流任务分派算法的有效性.

1 基于工作流任务的社会网络划分

通常，专家社会网络中存在着大量能够胜任各种工作流任务的专家服务候选者，因此，跨组织工作流任务分派应用系统可从专家社会网络中搜索出适合的专家服务，协同完成跨组织业务.例如，某个信息系统集成协同研究中心要组织完成一个大型的软件项目，为了提高软件项目质量，采用跨组织工作流技术进行管理，并将工作流任务分派到专家网络中的社会成员协同完成[13].其中，完成工作流任务的团队是一个关系紧密的整体，工作流任务要求人工服务具备软件工程(SE)、数据库(DB)、Web开发等专业知识技能.跨组织工作流任务分派框架如图2所示：

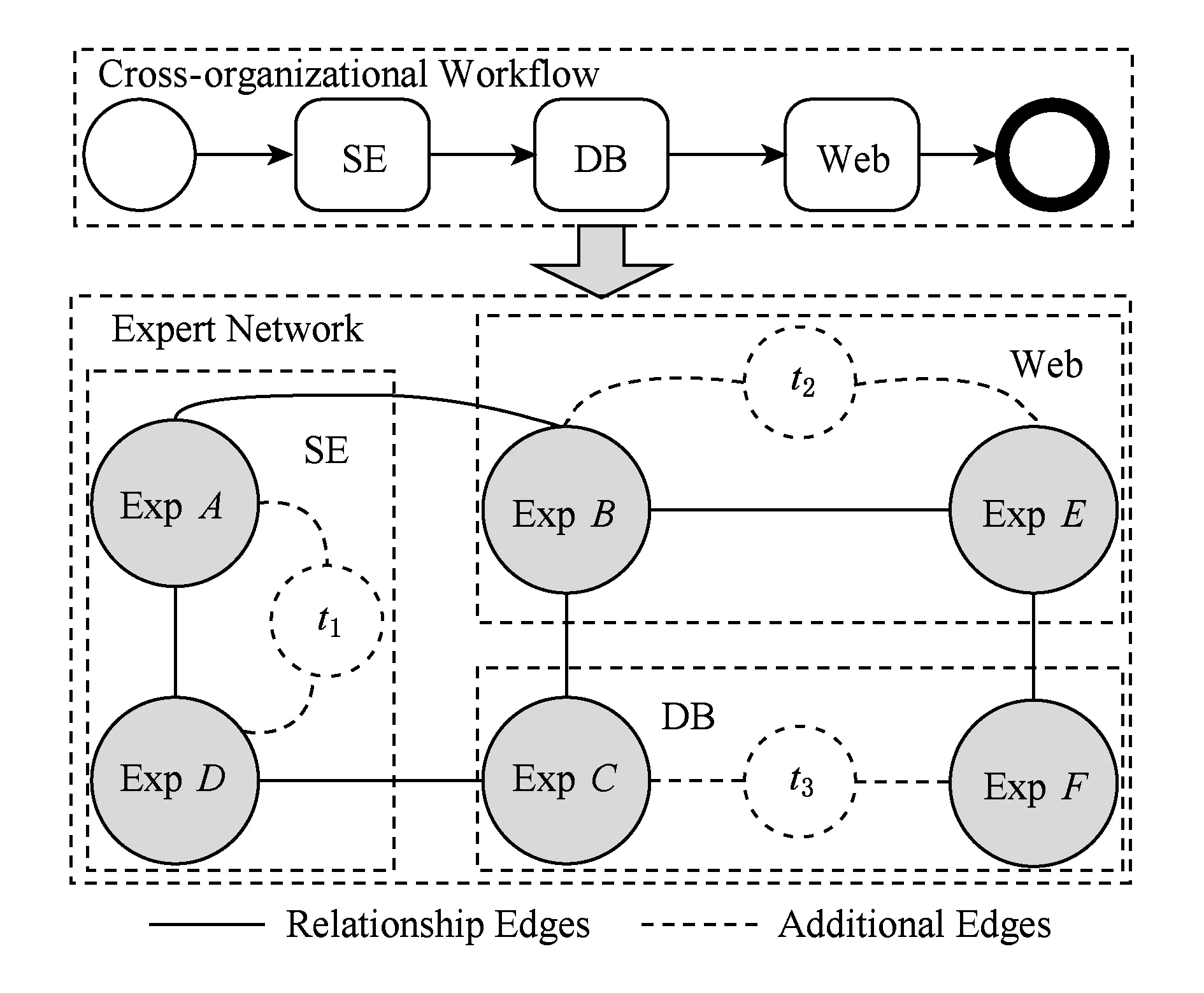
Fig. 2 Expert network graph based on partition with workflow tasks图2 基于工作流任务划分的专家社会网络图

针对专家社会网络的大规模性和复杂性等特点，从工作流任务功能出发，将社会网络进行分组描述，构建出一种基于任务子网划分的社会网络抽象图模型.首先，任务子网划分方法将工作流任务作为社会网络图节点，加入到专家候选者社会网络中；然后，将任务的专家候选者与相应的任务节点进行连接.通过增加任务节点和连接边，改变了原有社会网络的图结构，有利于提高工作流任务分派的计算效率.假定工作流任务集为T={ti|1≤i≤l}，任务ti作为新增节点加入到原网络图中，将任务ti的所有候选者节点与新增的任务节点相连，设置其连接边为较大的实数值D.例如，图2表示一个基于任务划分的社会网络图实例.

假设跨组织工作流应用需要完成p个任务，可根据工作流任务将社会网络划分成p个任务子网络，如果社会成员能够完成工作流任务ti，则将该成员划分到任务子网i中，相关概念和定义如下:

定义1. 任务子网图(subgraph).设任意2图G=(V,E,W)与GH=(VH,EH,WH)，如果VH⊆V，EH⊆VH×VH，则称图GH是图G的任务子网图.

定义2. 邻接节点(adjacent node).给定图G中的任意2个节点u和v，如果它们之间有边相连，则称节点u为节点v的邻接节点，

Adj(v)={u|(u,v)∈E∧u,v∈V}.

(1)

定义3. 任务子网连接点(connector).给定社会网络图G和基于工作流任务的某一划分方案P={G1,G2,…,Gp}，对于Gi中任意节点u∈Vi与Gj中任意节点v∈Vj，如果存在节点v∈Adj(u)，且Vi≠Vj，则称u是任务子网图Gi的连接点，记为u∈CN(Gi)；否则，称为内部节点，记为u∈IN(Gi).

定义4. 任务子网连接边(CEdge).给定社会网络图G和基于工作流任务的某一划分方案P={G1,G2,…,Gp}，对于划分方案P中任意相邻子图Gi和Gj之间的连接边可定义为

CEdge(Gi,Gj)={(v,u)|(v,u)∈

E∧(v∈CN(Gj))∧(u∈CN(Gi))}.

(2)

定义5. 任务子网内部边(IEdge).给定某一划分方案P={G1,G2,…,Gp}，对于划分方案P中任意子图Gj(1≤j≤p)，构造所有任务子网连接点的内部连接边，边的权重等于在该子图内部所计算出的连接点之间的最短路径值，称为任务子图内部边，其定义如下：

IEdge(Gi,Gj)={(v,u)|(v,u)∈

E∧(v∈CN(Gj))∧(u∈CN(Gi))}.

(3)

支持社会协同计算的跨组织工作流分派方法采用基于工作流任务子网划分的分层优化思想，将复杂的社会网络图进行有效地划分，依据划分后网络的拓扑特征，可简化任务分派中社会成员节点之间的最短路径近似计算和人工服务组合优化的问题，有利于降低大规模社会网络中人工服务搜索算法的时间复杂度.

2 任务成员社会关系评测算法

社会关系直接影响着跨组织业务项目的执行质量，在社会网络中，运用业务项目成员节点之间的最短路径距离值来描述成员之间的社会关系，因此，支持社会协同计算的跨组织工作流任务分派方法采用社会网络图的最短路径近似算法，实现工作流任务成员的社会关系评测.本节主要讨论社会网络成员节点之间的最短路径快速计算问题.

2.1 基于参考点的最短路径近似计算

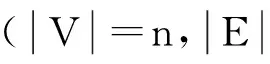
定义6. 最短路径参考点.在社会网络图中，选择k个参考点R={u1,u2,…,uk}，任意节点v到参考点的最短路径定义为θ(v)={d(v,u1),d(v,u2),…,d(v,uk)}，d(v,ui)为节点v与第i个参考点的距离，满足：

定理1. 三角不等式.任取3个网络节点s,u,t∈V，d(s,t)表示s与t之间的最短路径距离，则有：

d(s,t)≤d(s,u)+d(u,t)，

(4)

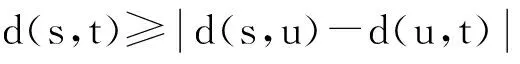
(5)

推论1. 假设存在路径πs,t∈SP(s,t)且u∈πs,t，则有：

d(s,t)=d(s,u)+d(u,t).

(6)

推论2. 假设存在路径πs,u∈SP(s,u)且t∈πs,u，则有：

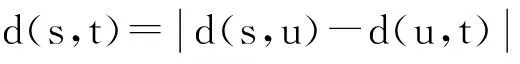
(7)

基于参考点的预先计算环节采用了深度优先算法，计算出参考点K={u1,u2,…,uk-1,uk}与网络其他节点之间的最短路径距离，根据三角不等式定理可知：

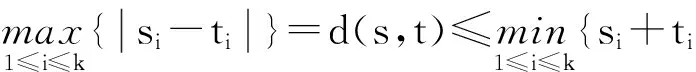
(8)

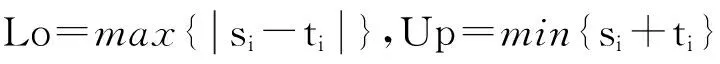
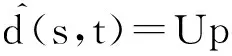
(9)

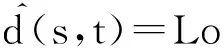
(10)

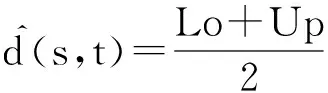
(11)

(12)

2.2 基于任务子网划分的参考点选取

参考点选取是基于参考点的最短路径近似算法的最重要部分，其选取结果直接影响着最短距离计算的正确性和效率.然而，参考点的选择算法是NP-hard问题[13].为提高最短路径近似算法的正确性和时间效率，设计了一种适用于社会工作流任务分派的参考点选取策略，根据划分后社会网络的结构特征，选择任务子网连接点作为参考点，因为，任意2个任务子网节点之间的最短路径必然经过任务子网的连接点.如图3所示，其中，深色点表示任务子网图的连接点，虚连接线表示子网之间的连接边，以图3中节点a,b,c,d,e,f为例，它们之间的最短路径都是经过所选的参考点，即任务子网的连接点.

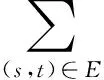
命题1. 在处理不同子网成员的社会关系评测时，采用基于参考点的最短路径算法，并以工作流任务子网连接点作为参考点，称之为基于任务子网连接点的最短路径算法，该算法和Dijkstra最短路径算法具有相同的准确度.

证明. 由基于任务子网的参考点选取示意图可知，不同工作流任务子网成员之间的最短路径必然经过任务子网的连接点，由推论1可得：d(s,t)=d(s,connector)+d(connector,t)，其中s,t是不同任务子网的2个节点，至少有一个参考点出现在s,t之间的最短路径时，则Landmark(s,t)=1.根据三角不等式可知，在处理不同子网成员的社会关系评测时，以任务子网连接点作为参考点的最短路径算法和Dijkstra最短路径算法具有相同的准确度.

证毕.

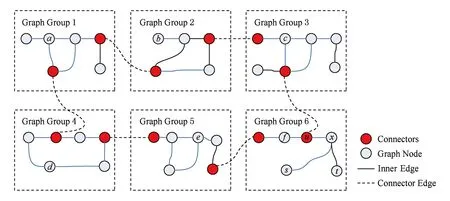
Fig. 3 Reference point selection based task subgraph partition图3 基于任务子网划分的参考点选取示意图

2.3 基于任务子网划分的数据存储

基于任务子网连接点的最短路径算法采用数据预处理环节，通过预先计算生成的辅助数据，提高后续算法的执行效率.不同于文献[14-16]的存储方法，本文设计了一种基于任务子网分层的存储方案.在预计算阶段，首先，执行基于任务子网连接点的最短路径生成树算法，不仅存储每个候选节点vi到子网连接点u之间的最短距离，而且存储每个节点到子网连接点的最短路径(vi,pu[vi],pu[pu[vi]],…,u)，其中，pu[vi]是vi生成树的父节点，通过运用父节点查找算法，可准确计算出每一个节点到参考点的最短路径；然后，按照工作流任务功能进行分类，存储子网参考点到子网内部节点之间的最短路径、距离以及功能属性值；最后，存储高一级的参考点网络.

基于任务子网分层的存储方案不需要存储所有节点到参考点之间的最短路径信息，只需按任务功能分类，存储子网内部节点到相应参考点的信息，有效地减少了存储空间；同时，在分析2个节点之间的最短路径时，只需计算候选者节点到其任务子网连接点之间的最短距离，因此，提高了近似算法的计算效率.

2.4 不同子网成员的社会关系评测

针对不同子网成员的社会关系评测问题，讨论了3种算法：1)采用以任务子网连接点作为参考点的选取策略，设计一种最基本的社会关系评测算法，即基于任务子网连接点的最短路径算法(ConnSPT)；2)采用任务子网分层策略，提出一种基于任务子网连接点的分层最短路径算法(LayeredSPT)；3)通过定义任务子网距离，提出基于任务子网距离的最短路径近似算法(LTaskSPT).

2.4.1 基于任务子网连接点的最短路径算法

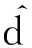
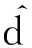
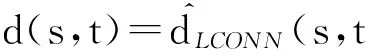
证毕.

根据命题2分析，基于任务子网连接点的社会成员关系评测的实现描述如算法1：

算法1. 基于任务子网连接点的社会成员关系评测算法.

输入：工作流任务Task={ta1,ta2,…,tak}、候选者网络图G=(V,E,W)；

输出：s,t两点之间近似距离.

① 计算节点s和t到其所属的任务子网的连接点集合connList；

② foreachconninconnListdo

③ps→t=ps→conn∘pconn→t；

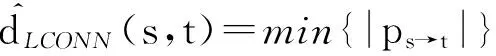
⑤ end for

算法1中ps→conn∘pconn→t的符号∘表示ps→conn和pconn→t两条路径的连接符，假设ps→conn={u1,u2,…,ui,ui+1}和pconn→t={v1,v2,…,vj,vj+1}，存在ui+1=v1，且ui+1和v1是子网连接点，则可表示为ps→t=ps→conn∘pconn→t.

2.4.2 基于任务子网连接点的分层最短路径算法

基于任务子网连接点的分层最短路径算法融合了任务子网分层策略，根据社会网络的任务划分，将原社会网络构建为2层网络的分层结构.其中，特殊节点作为高一级抽象网络层，通过去除中间节点进行化简，化简后的各个任务功能网络相对独立，任务子网之间通过少量的边连接起来，这部分边的端点称为子网连接点(connector)以及功能子网内部的连接边共同构成高一层网络，采用基于任务子网参考点的分层策略能够有效地降低最短路径近似算法的复杂度.

假设ps→i Conn为节点s到其所属子网i连接点iConn的最短路径，pj Conn→t为节点t所属子网j的连接点jConn到节点t的最短路径，pi Conn→j Conn表示任务子网i的所有连接点和子网j的所有连接点之间的最短路径，其长度称为分层子网距离，则有ps→t=ps→i Conn∘pi Conn→j Conn∘pj Conn→t，基于任务子网连接点的分层最短路径近似算法的计算模型可定义为

|pi Conn→j Conn|+|pj Conn→t|}.

(13)

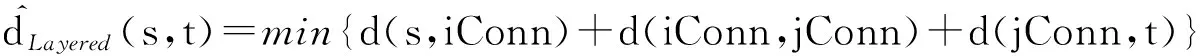
根据分层最短路径的近似计算模型分析，基于任务子网连接点的分层最短路径近似算法的实现步骤如算法2：

算法2. 基于任务子网连接点的分层最短路径近似算法.

输入：工作流任务Task={ta1,ta2,…,tak}、候选者网络图G=(V,E,W)；

输出：s,t两点之间近似距离.

① 计算节点s到其所属的任务子网i的连接点最短路径ps→i Conn，其中iConn表示子网i的连接点；

② 计算节点t到其所属任务子网j的连接点最短路径pt→j Conn，其中jConn表示子网j的连接点；

③ 计算子网连接点之间的最短路径pi Conn→j Conn；

④ 融合分层策略的所有最短路径联合:ps→t=ps→i Conn∘pi Conn→j Conn∘pj Conn→t；

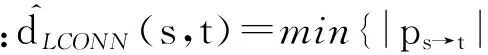
2.4.3 基于任务子网距离的最短路径近似算法

基于任务子网连接点的分层最短路径近似算法可以提高计算速度，并且能够保证较高的正确率.但是，基于任务子网连接点的分层最短路径近似算法需要计算两任务子网的所有连接点之间的最短距离，当两任务子网的连接点太多时，该近似算法的时间性能会受到极大的影响.为进一步提高算法的计算效率，定义了一种任务子网距离，以任务子网距离代替连接点之间的最短距离计算，任务子网距离定义如下：

定义7. 任务子网距离.给定任意2个工作流任务子图SubGH1,SubGH2，则有任务子网距离可定义为

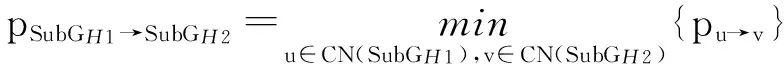
(14)

其中，CN(SubGH1)是子网SubGH1连接点集合，CN(SubGH2)是子网SubGH2连接点集合.

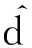
2.5 子网内部成员的社会关系评测

基于任务子网连接点的最短路径近似算法适用于评测不同子网的成员关系，但不能准确地评测同一子网内部的成员关系，因此，本节内容主要讨论关于任务子网内部的成员关系评测算法，相关定义如下[16]：

定义8. 最短路径生成树.给定任意某一任务子图GH=(VH,EH,WH)，基于参考点的本地最短路径树是以对应该子网的某一参考点r∈RH为根的生成树，子网内所有节点v∈VH到根节点的路径是r和v的最短路径，路径长度是r和v最短距离值.

定义9. 最近公共祖先.给定某一有根树Tree及树中2个节点u,v，最近公共祖先LCA(Tree,u,v)表示一个节点x，满足x是u,v的祖先且x的深度尽可能大.

根据定义8和定义9，采用了一种基于最近公共祖先的子网内部成员关系评测方法.假设评测同一任务子网i成员s到t之间的关系，首先计算基于参考点的本地最短路径树；然后计算成员s和t最近公共祖先LCA(Treei,s,t)，则同一子网内部成员关系的估算方法为

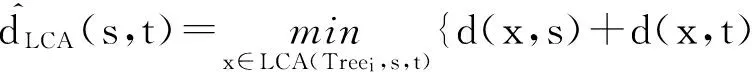
(15)

命题3. 给定某一任务子图GH=(VH,EH,WH)、子网连接点集合R，∀s,t∈VH，则有

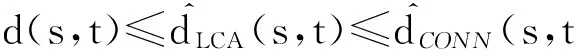
(16)

∀u∈R,x∈LCA(Treei,s,t)，则有

d(s,u)+d(u,t)=d(s,x)+d(x,t)+2d(u,x).

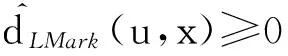
d(s,u)+d(u,t)≥d(s,x)+d(x,t)，

进一步计算可得

，

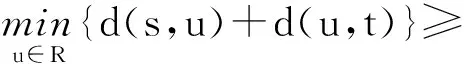
则可得

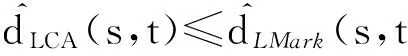
证毕.

为了快速地评测子网内部成员的关系，根据命题3分析，子网内部成员的关系评测算法可计算为

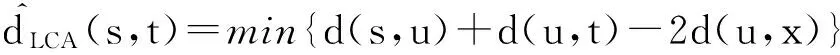
(17)

其中，x∈LCA(Treei,s,t),u∈R.

根据式(15)～(17)分析，本文采用了基于最近公共祖先的最短路径算法，评测子网内部社会成员关系.运用基于任务子网分层的存储方案存储每个子网参考点到任务子网内部节点之间的最短距离和最短路径.因此，所提出的子网内部的任务成员关系评测算法只需直接从分层存储文件中查询，即可快速准确地评测出同一子网内部成员之间的关系.

3 跨组织工作流任务分派优化算法

为确保跨组织业务项目的顺利进行，要求项目领导者能够协调好不同组织成员之间的关系，即优选出的领导者必须与每个任务协作伙伴成员之间具有良好密切的社会关系.因此，在面向大规模社会网络进行协同计算时，跨组织工作流分派优化算法需解决2个问题：1)如何从大规模专家社会网络中快速地选择出领导者节点，从而负责分派任务并协调管理任务协作伙伴成员之间的交互；2)如何从大规模专家社会网络中高效率地选择工作流任务协作伙伴，确保任务协作成员与领导者之间协同工作的效率.

传统带领导节点的团队任务分派采用了蛮力法(Brute-Force)实现[6].Brute-Force算法以所有的社会网络成员作为领导候选者；然后，遍历社会网络中子任务对应的全部候选者节点，查询出与领导者沟通代价最优的子任务协作伙伴；最后，通过比较所有的专家服务组合方案，优选出领导者及相应任务协作成员节点的团队组合，其中子任务协作成员与领导者之间的协同交互成本越低越好.

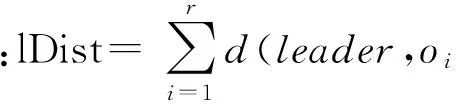
根据定义10分析，跨组织工作流活动执行前需要分派人工任务，即在工作流任务和专家社会网络之间建立映射关系，形成协同成本最优的专家团队组合，从而保证跨组织工作流专家服务资源的合理配置.实质上，支持社会协同计算的跨组织工作流任务分派是一个面向社会网络的团队组合求解问题.

问题1. 专家团队组合求解.给定跨组织工作流任务Task和一个候选专家社会网络G，支持社会协同计算的跨组织工作流任务分派模型主要目标是：搜寻一组专家团队成员，团队成员的所有技能满足跨组织项目任务Task的需求，并使得跨组织项目团队的协同交互成本最小，形式化定义如下：

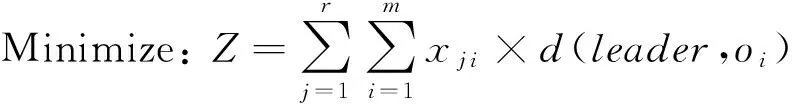
(18)

(19)

其中，xj i是布尔变量，当工作流任务tj选择第i个专家时xj i=1，否则xj i=0.跨组织项目是由多个子任务组成，实际上面向工作流任务分派算法针对每一个子任务，专家社会网络存在着大量候选专家.以2006年的DBLP数据集为例，DBLP存在着4 802个关于Web问题的研究专家，5 140个专家从事DW方面的研究，其中大量专家之间存在着相互关系，他们形成了复杂的大规模社会网络.因此，从该网络中选取出项目领导者，以及计算出所有任务候选专家到领导者节点之间的最短路径，都需要大量的计算时间.

基于蛮力法的团队任务分派算法能够查找出交互成本最优的解决方案，但产生了大量的计算成本，不适用于复杂社会网络.为了提高算法的性能，Juang等人[7]采用社会计算的重要概念介数中心性(betweenness centrality)，提出了2种选择领导者节点的算法：BCinDijkstra和SSinDijkstra[7]，在此基础上，从社会网络中选择与领导节点交互成本最优的每个任务协作伙伴成员，即距离领导者节点最近的任务子网候选者节点.基于介数中心性方法确定的领导者节点具有高的介数中心性，因此总是在多数社会成员节点之间的最短路径上，提高了所选工作流任务成员与领导者的高效协同工作的可能性.

介数中心性是Freeman[17]于1977年提出的，用于衡量社会成员节点的社会地位和交互协调性.2001年，Brandes[18]提出了一种快速介数中心性的计算方法，主要思路为：首先任取一个节点开始，通过Dijkstra计算经过节点的最短路径数；然后反向累加计算节点的介数中心性[19].在大规模社会网络中[20-21]，Brandes算法在计算节点之间的最短路径时，需要耗费大量的计算成本，其效率不高.而且，在没有进行任务子网划分的原始社会网络中，搜索相应工作流任务的团队协作伙伴成员，必须遍历整个社会网络图，才能查询出合适的子任务协作伙伴.

通过观察工作流任务子网划分的社会网络特征，我们发现：任务子网连接点总存在于2个不同任务子网节点之间的最短路径上，2个子网候选节点的交互必然会经过子网的连接点.因此，领导者与其他任务子网的所有节点之间的最短路径必然会经过子网连接点.如图4所示，任务子网GroupA的连接点a在领导节点leader与GroupA中所有节点之间的最短路径上.

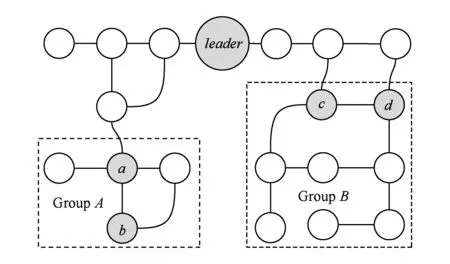
Fig. 4 Example of finding workflow task members图4 工作流任务协作成员选择实例

基于划分后社会网络特征分析，任务协作伙伴节点必然是任务子网连接点之一，因此，社会协同计算方法在为领导者查找任务协作伙伴时，只需在任务子网连接点集合中搜索，简化了工作流任务分派算法的复杂度.

命题4. 给定某一任务子图SubGH=(VH,EH,WH)，已选领导者节点leader∉VH，子网连接点集合R⊆VH,设与领导节点交互成本最优的子任务协作者为mem，则有mem∈R.

证明. 假设mem∈VH是任务子网SubGH所选出的任务协作者，且mem∉R.由于leader∉VH,不同任务子网成员之间的最短路径必然经过连接点，因此，存在连接点conn∈R，且conn在leader与mem节点之间的最短路径上.

根据推论1可得到:d(leader,mem)=d(leader,conn)+d(conn,mem)，且d(conn,mem)≥0.

则d(leader,mem)≥d(leader,conn)，可推出mem不是协作交互成本最低的项目协作伙伴.

因此，只有当mem∈R时，候选节点mem才是团队最优的任务协作者.

证毕.

由命题4分析可知，社会协同计算应用只需在工作流任务子网连接点集合中搜索子任务协作伙伴，减少了任务协作伙伴的搜索时间，提高了社会协同计算的时间效率.而且，从命题4的结论反推，逆向思考可知，距离所有任务子网连接点越近的社会成员节点，越有可能被选作为领导者节点，因为，社会协同计算模型要求所选取的领导者必须与每个任务协作伙伴成员之间具有良好密切的社会关系.受此启发，根据工作流任务划分后的社会网络特征，在借鉴Brandes算法思想的基础上，本文创新性提出了一种基于任务子网连接点的快速介数中心性算法，用于快速地搜索领导者节点.

定义11. 基于任务子网连接点的介数中心性.令σ(s,t)表示节点对(s,t)的最短路径数量，σ(s,t|v)表示节点对(s,t)的最短路径通过v的数量，子网连接点conn∈R，则基于子网连接点的介数中心性可定义为

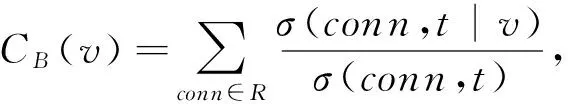
(20)

其中，若conn=t，则σ(conn,t)=1;若v∈r,t，则σ(conn,t|v)=0.

由定义11可知，经过节点的最短路径数量决定了其在社会网络中的介数中心性值.首先，基于任务子网连接点的快速介数中心性算法任取一个任务子网连接点conn，并将conn定义为源节点，采用Dijkstra最短路径算法，遍历基于任务子网划分的候选者网络图，计算经过候选节点的最短路径数.在以节点conn开始的最短路径中，候选节点w的父节点可表示为

Pconn(w)={u:(u,w)∈E,d(conn,w)=

d(conn,u)+d(u,w)}，

(21)

则有

(22)

因为到达节点u的最短路径也通过边(u,w)到达节点w，在进行Dijkstra算法遍历时，可根据式(21)(22)，计算出从任务子网连接点出发经过每个节点最短路径数量.Dijkstra算法复杂度为O(m+nlogn)，因此，采用基于任务子网连接点的快速介数中心性算法分析时，经过社会网络图中候选节点的最短路径数量的统计时间复杂度为O(Rnum×m+Rnum×nlogn).

候选节点v的介数中心性表示经过节点v的最短路径数量比例，其值越高，则节点v就越重要，对工作流任务子网连接点的影响也越大.为了简化计算，将通过节点v最短路径的数量比例定义为节点依赖度:

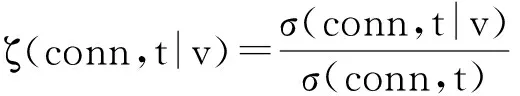
(23)

根据式(20)～(23)分析，根据节点依赖度的定义，可推导出命题5.

命题5. 假定工作流任务子网连接点conn∈R，在社会网络中conn经过节点v到其他成员节点存在着最短路径，则可知节点v的介数中心性可满足：

ζ(conn|v)=

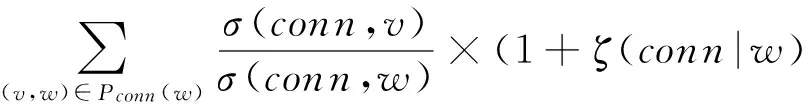
(24)

证明. 根据式(23)，可知：

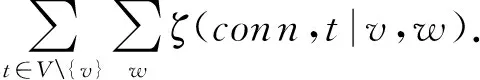
因为

σ(conn,t|v,w)=

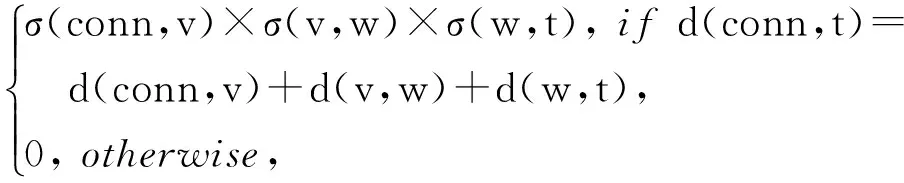
则有

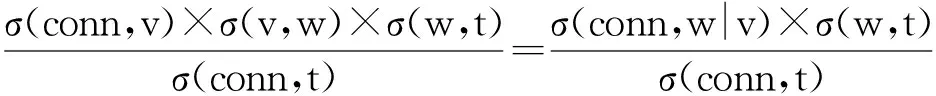
整理可得

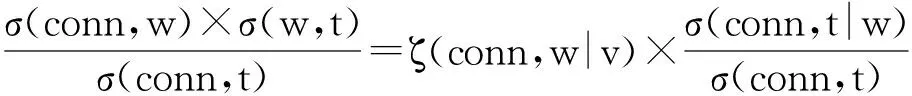
根据节点模型依赖度定义，可知

ζ(conn,t|v,w)=ζ(conn,w|v)×ζ(conn,t|w),

因此，

又因为

for (v,w)∈Pconn(w)，

fort=w，

则有

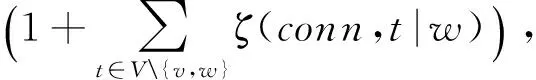
即

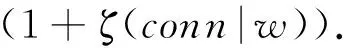
证毕.

由命题5分析可知，领导节点计算方法为

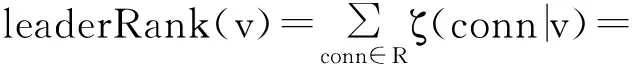
(25)

基于任务子网连接点的快速介数中心性算法以任务子网连接点conn∈R为源点，首先进行正向计算，采用Dijkstra算法生成最短路径树，通过节点w的前驱节点v计算w的最短路径数目；然后进行反向搜索，从最短路径生成树的叶节点反向遍历所有节点，通过节点w计算其父节点v的介数中心性，具体实现见算法3.

算法3. 基于任务子网连接点的介数中心性算法.

输入：工作流任务Task={ta1,ta2,…,tak}、候选者网络图G=(V,E,W)；

输出：Top-k领导者节点集.

① 基于任务的社会网络划分：GH=(VH,EH,WH)←(V,E,W)；

② foreachconn∈Rdo*遍历所有子网连接点*

③ 最短路径计算：Dijkstra(conn)；

④ 存储w前驱节点：P[w]←v；

⑤ 统计通过w的最短路径数量：σ[w]←σ[w]+σ[v]；

⑥ 将从起点到当前点的距离压入栈：S←v；

⑦ end for

⑧ 初始化：ζ[v]←0；

⑨ whileS≠null do

⑩ 出栈：w←S；

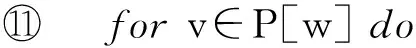
基于任务子网连接点的介数中心性算法的时间复杂度为O(Rnum×m+Rnum×nlogn).当基于任务划分的社会网络中连接点非常少时，相比Brandes算法，所提出的领导者评价算法具有良好的时间性能.

在确定领导者后，根据命题4，支持社会协同计算的工作流分派方法的具体实现步骤如算法4.

算法4. 支持社会协同计算的工作流任务分派算法.

输入：工作流任务Task={ta1,ta2,…,tak}、候选者网络图GH=(VH,EH,WH)←(V,E,W)；

输出：跨组织工作流协同计算解决方案wSolution.

① 基于任务子网连接点的介数中心性算法：leader←getLeader(GH)；

② 将选取的leader加入解决方案中：wSolution.add(leader);

③ 分析leader所胜任的工作流任务：taskList←getCapbility(leader)；

④ 基于子网划分的任务协作者遍历搜索算法；

⑤ foreachTaskinrequiredTasksdo*遍历跨组织工作流所有任务*

⑥ ifTaskinTaskListthen

⑦ continue；

⑧ end if

⑨ 获取工作流任务子网对应的所有连接点：memList←getConnectors(Task)；

⑩ formeminmemListdo*遍历任务子网连接点*

支持社会协同计算的工作流任务分派算法包括2部分：基于快速中心性计算的领导者选择和子任务团队协作成员查询.根据算法3的分析已知，领导者节点确定算法的时间复杂度为O(Rnum×m+Rnum×nlogn)；在进行子任务团队协作成员评估分析时，需计算最短路径d(mem,leader)，采用Dijkstra最短路径算法，计算所有子任务协作成员的时间复杂度为O(l×Rnum+l×nlogn)，其中l表示工作流任务的数量.综上分析，支持社会协同计算的工作流任务分派算法的时间复杂度为O(Rnum×(l+m)+(l+Rnum)×nlogn)，其中m≫Rnum≫l.

4 仿真实验

4.1 数据准备与分析

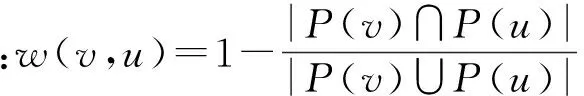
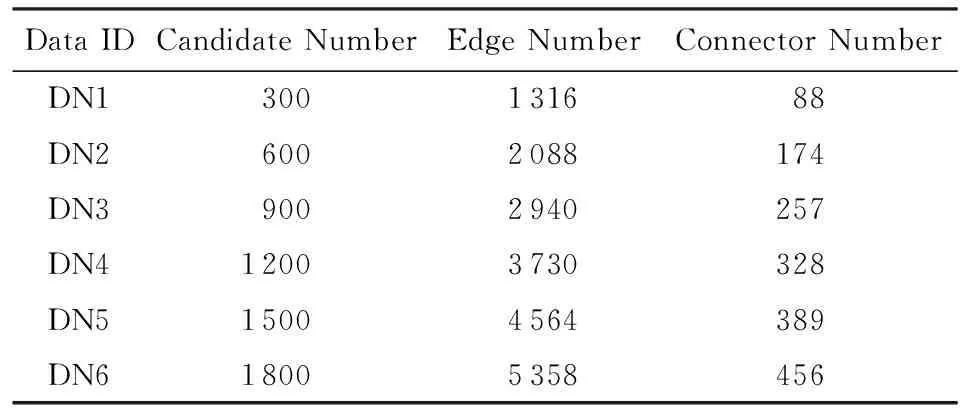
Table 1 DBLP Data Analysis

假定面向专家社会网络的跨组织业务应用需要6个不同研究方向的专家服务，以协同完成跨组织工作流的所有任务，其中包括算法(AL)、软件工程(SE)、数据库系统(DB)以及Web程序设计(Web)等方面的专家，如图5所示：

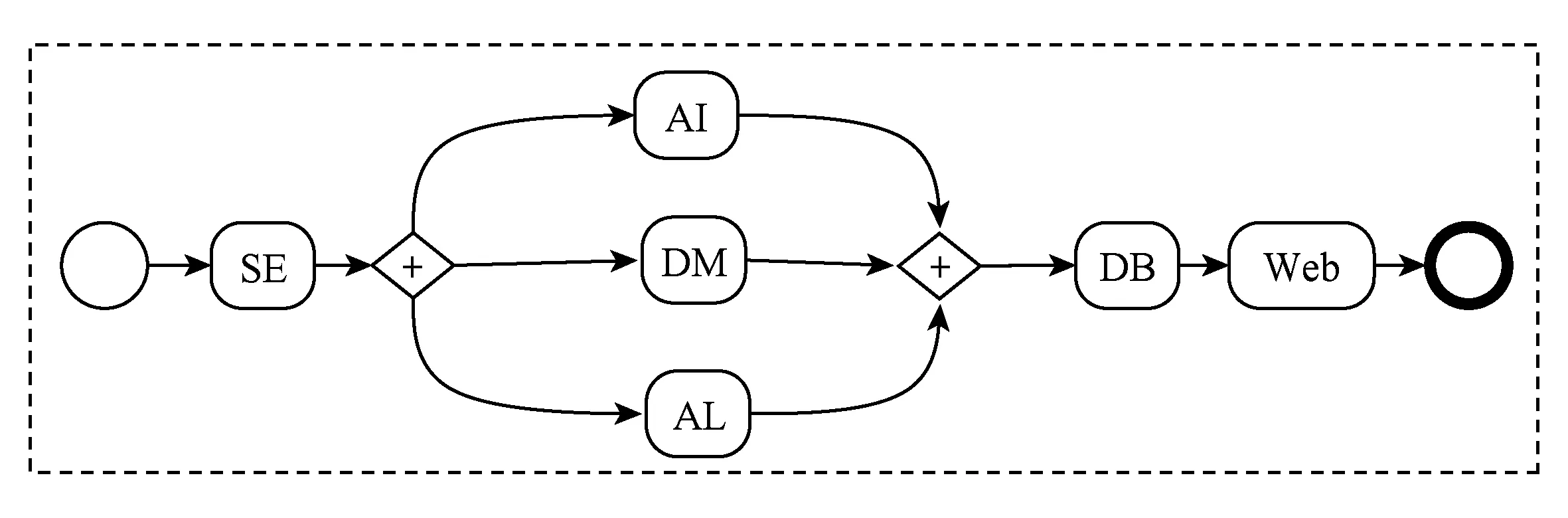
Fig. 5 Cross-organizational workflow application for expert tasks图5 面向人工任务的跨组织工作流应用实例

仿真实验首先按照文献[6]方法生成了DBLP专家社会网络图，然后采用了本文第1节阐述的基于任务的社会网络划分方法，根据每个候选者节点的功能角色划分出不同任务子网，划分后专家社会网络如图6和图7所示.

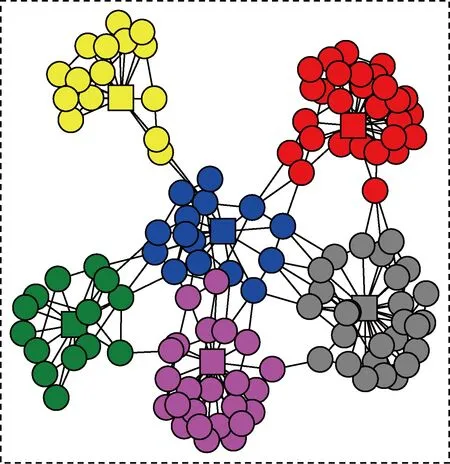
Fig. 6 Graph grouped by task types图6 基于任务的子网划分

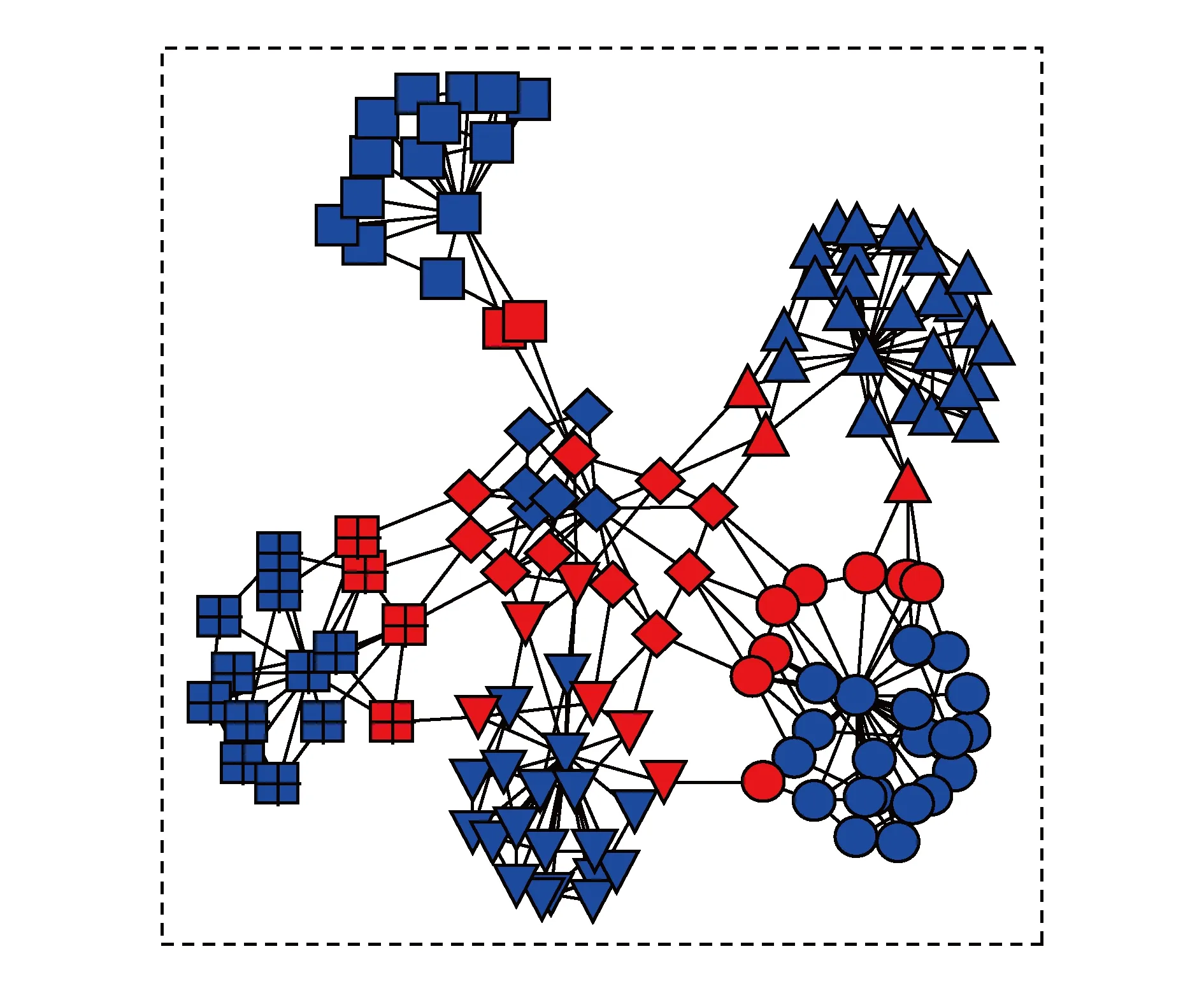
Fig. 7 Graph classified by connectors图7 基于连接点的成员分类

图6中不同颜色表示不同任务子网.社会协同计算的相关算法都涉及到基于任务子网连接点的分析方法.因此，在工作流任务子网划分图的基础上，可视化仿真实验根据任务子网连接点对所有的社会成员节点进行了分类，如图7所示.其中，所有红色图形都表示工作流任务子网连接点，不同图案表示不同任务候选者节点.由可视化分析实验可知，工作流任务子网连接点存在于2个不同子网之间，而且，其数量远小于非连接点.

4.2 社会关系评测算法分析

本节仿真实验分析了本文所提出的社会关系评测算法，验证了该算法在社会网络环境下解决社会工作流任务分派问题的可行性，其中，共设计了2个实验：实验1主要是分析了不同子网社会成员之间的关系评测算法；实验2则主要是分析了子网内部社会成员之间的关系评测算法.根据最短路径近似算法获取社会成员的关系评价值，采用式(26)评估最短路径近似算法的正确率.

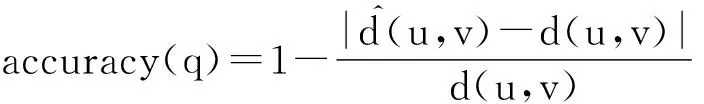
(26)

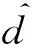
实验1. 不同任务子网社会成员的关系评测算法分析验证.

按表1和基于任务的社会网络划分方法构建了不同规模的DBLP专家网络，随机选取2个任务子网，采用本文提出的近似最短路径算法，计算出不同子网之间的所有节点的最短距离值.实验1采用柱状图分析了基于任务子网连接点的最短路径计算方法(ConnSPT)、基于任务子网连接点的分层最短路径计算方法(LayeredSPT)以及基于任务子网距离的最短路径近似计算方法(LTaskSPT)的正确率，如图8所示.

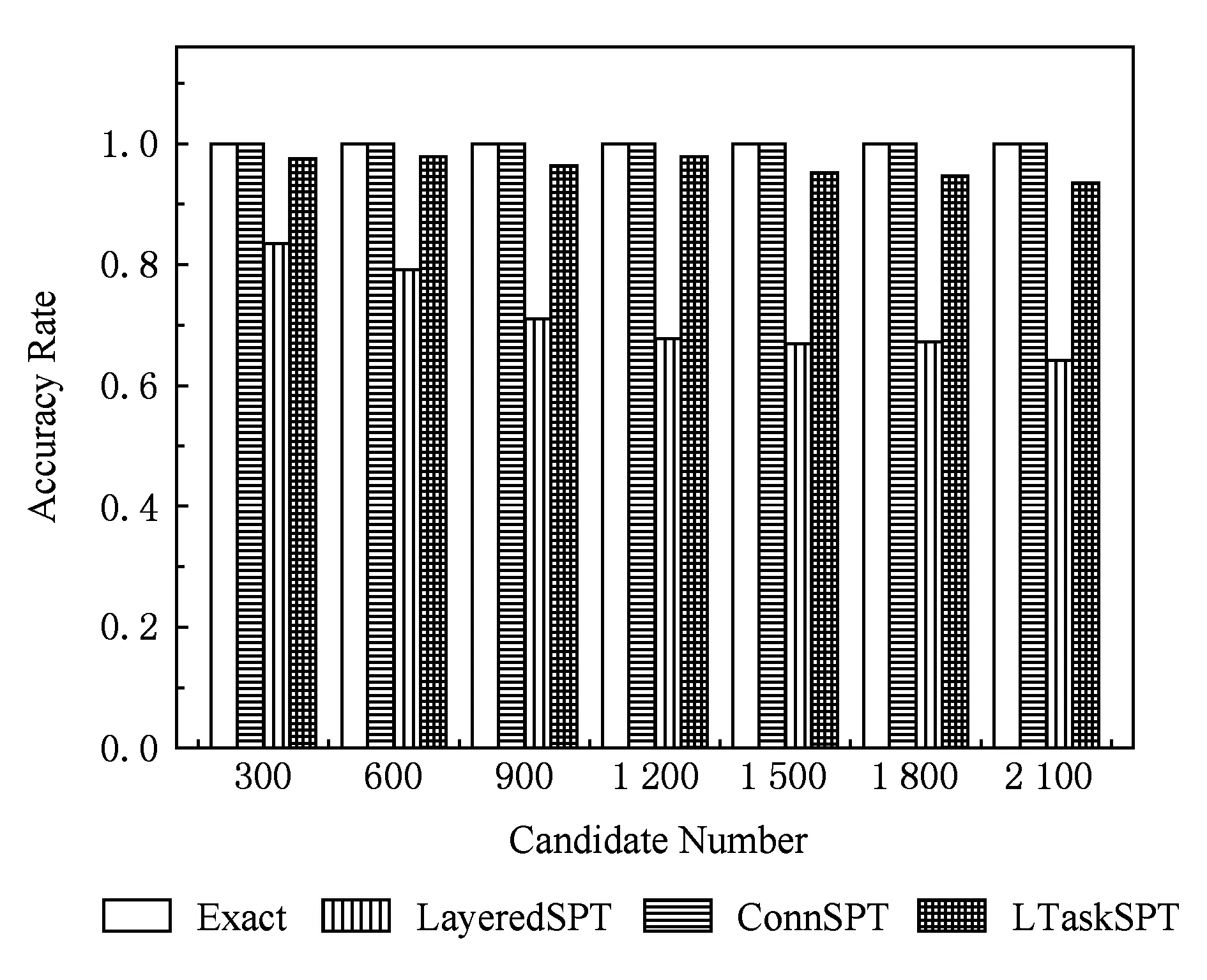
Fig. 8 Correctness verification of different group member relation图8 不同子网的社会关系评测算法正确率分析

通过观察图8可知，基于任务子网连接点的最短路径算法的准确率为1；基于任务子网连接点的分层最短路径算法也有较好的准确率，其准确率的平均值达到了0.97；基于任务子网距离的最短路径近似算法的正确率相对较差，其准确率的平均值为0.72.实验结果表明ConnSPT算法的正确率最好，而LTaskSPT算法的正确率是3种近似算法中相对较差的.

算法的时间性能是评价面向复杂社会网络的成员关系评测算法可行性的重要指标.为检验所提近似算法在不同网络规模下的性能，仿真实验采用6种不同规模的社会网络分析了所提算法的性能，如图9和10所示.

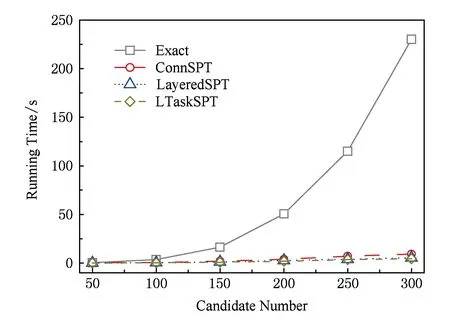
Fig. 9 Performance evaluation of group member relation图9 不同子网的社会关系评测算法性能分析

通过观察图9可知，本文提出的3种不同任务子网社会成员的社会关系评测算法的时间性能明显优于精确的最短路径计算方法.而且，随着专家候选者的数量不断增多时，所提算法的性能优势表现得更加显著.实验结果表明，精确的最短路径算法的时间花费远大于所提近似算法的时间花费.

图10是为了更加清晰地分析所提算法的性能效率，删除了描述精确最短路径算法的性能曲线，主要展示了本文所提出的3种最短路径近似算法的时间性能.

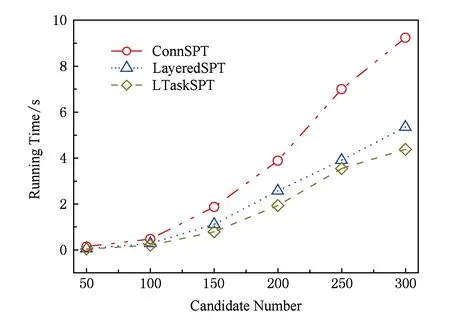
Fig. 10 Details of Fig. 9图10 图9中算法性能的详细表示

由图10可知，基于任务子网距离的最短路径近似算法的性能效率最优，基于任务子网连接点的分层最短路径算法次之，而基于任务子网连接点的最短路径算法效率相对差一些.与算法准确率实验表现出的情况刚好相反，因此，我们可以根据业务的需要，选择适合的社会关系评测方法.

实验2. 子网内部社会成员关系评测算法分析.

采用与实验1同样的方法，设置了不同规模的DBLP专家网络，任取一子网，采用本文所提的子网内部社会成员关系评测算法，计算子网内部不同节点的最短路径距离值.实验2采用柱状图分析了基于最近公共祖先的最短路径算法(LCASPT)和基于任务子网连接点的最短路径算法(ConnSPT)的正确率.如图11所示，基于最近公共祖先的最短路径算法正确率接近1；基于任务子网连接点的分层最短路径算法也有较好的正确率，正确率在0.6上下，不适用于同一子网关系评测.

为检验子网内部社会成员关系评测算法的时间性能，仿真实验比较了基于最近公共祖先的最短路径算法(LCASPT)和精确的最短路径算法(Exact)的性能，如图12所示.其中，虚线条表示采用的LCASPT算法，而实线条表示Exact算法的性能.观察图12可知，基于最近公共祖先的最短路径近似算法的性能明显优于精确的最短路径算法.

实验1和实验2验证分析了本文提出的社会关系评测算法，实验结果表明，本文提出的社会成员评测算法具有良好的时间性能，保证了较高的精确度，为面向大规模社会网络的跨组织工作流任务分派提供了技术支持.

4.3 支持社会协同计算的工作流任务分派算法分析

仿真实验进一步通过分析社会工作流的协同模型算法，验证了所提出的算法在复杂社会网络环境下解决工作流多任务外包问题的可行性.为此，设计了3个方面实验，其中，实验3主要验证了基于任务子网连接点的介数中心性算法的性能效率，即分析领导者选取算法的效率问题；实验4分析了基于子网划分的任务协作者遍历搜索算法的性能效率；实验5验证了面向社会工作流的协同计算模型算法的正确性.

实验3. 基于任务子网连接点的介数中心性算法的性能效率分析.

社会化网络为工作流任务提供了大量的专家候选者以及他们之间的社会关系信息.然而，社会网络所固有的复杂性和大规模性也给工作流协同模型算法的计算效率带来了挑战.为分析领导者选取算法的可行性，实验3通过分析比较Kargar和An[6]以及Juang等人[7]提出的领导者选择算法，验证所提出的基于任务子网的快速介数中性算法(ConnBC)的性能效率.实验3中以图5工作流为例，工作流业务包括了6个任务，通过选取不同规模的实验数据来分析算法性能，其中候选者节点规模集合为{300,600,900,1 200,1 500,1 800}.每次实验执行10次，取其平均值作为实验结果.如图13所示，所提算法ConnBC具有更好的时间性能，而且，随着候选者数据量增大，表现则更加明显.

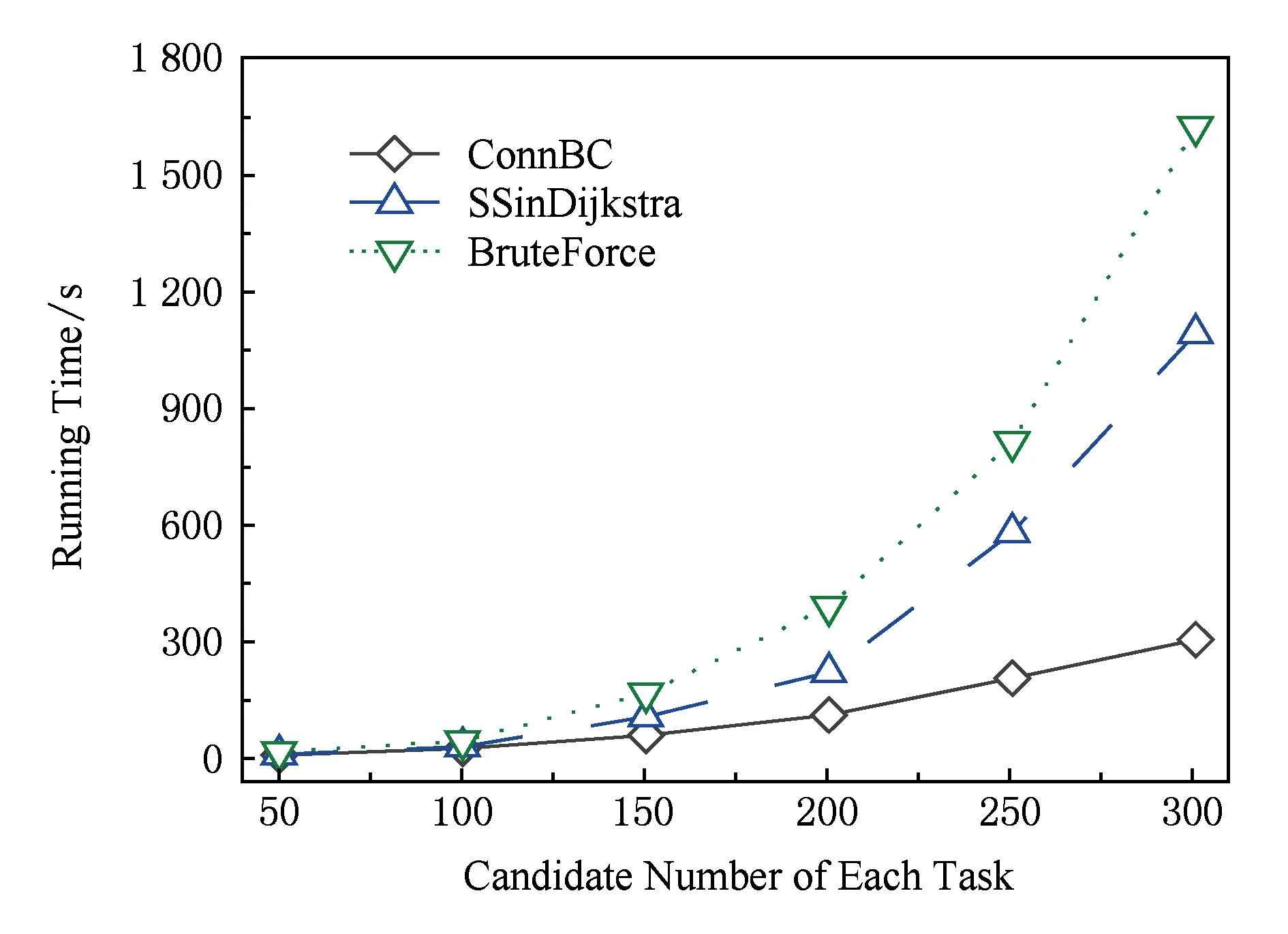
Fig. 13 Performance evaluation of leader selection图13 领导者选取算法性能分析

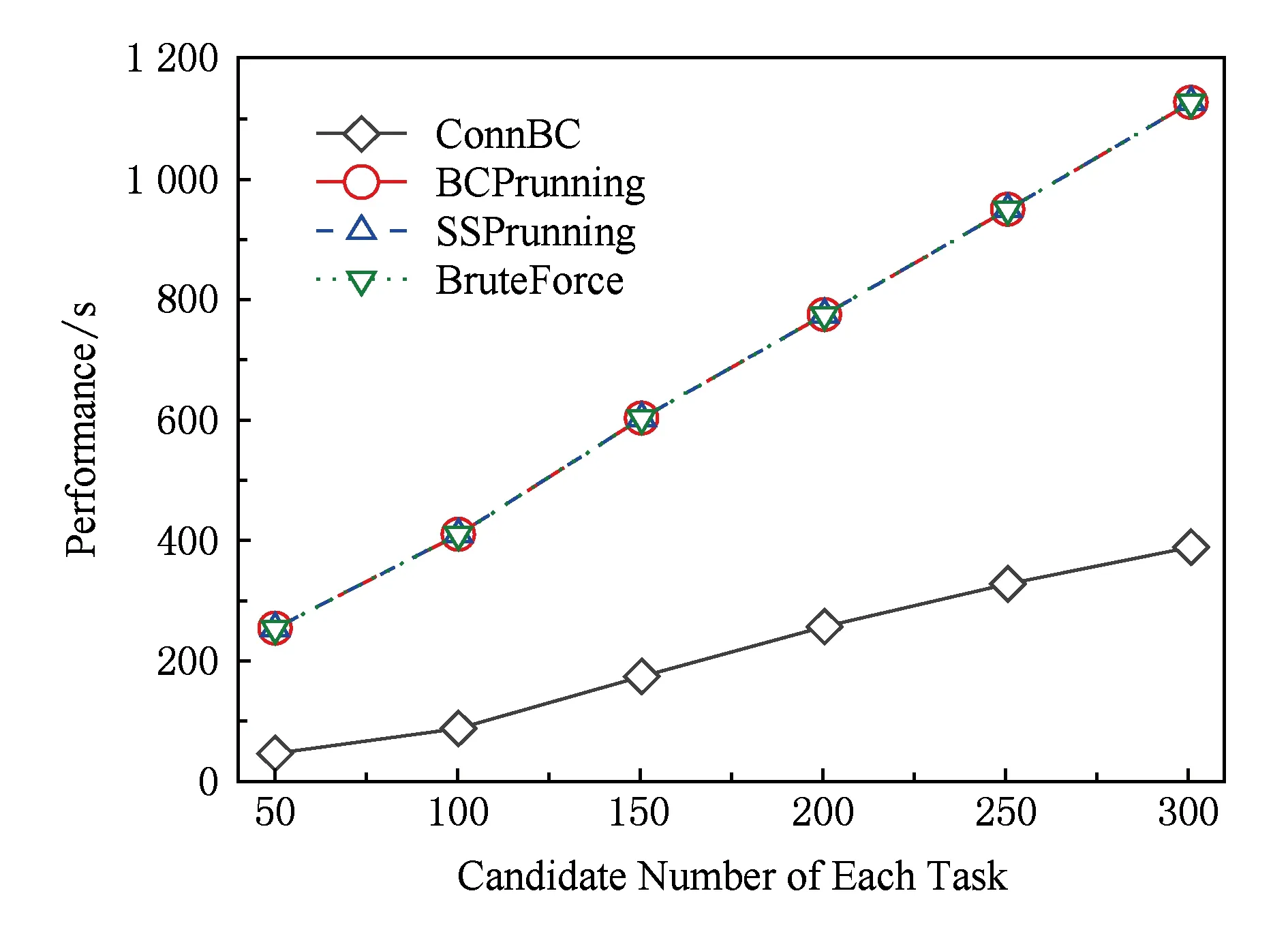
Fig. 14 Performance evaluation of group member discovery图14 任务协作者搜索算法性能分析

实验4. 基于子网划分的任务协作者遍历搜索算法性能分析.

为分析任务协作者搜索算法效率，实验4分析了Kargar和An[6]以及Juang等人[7]提出的算法，并与所提出的基于任务子网划分的任务协作者搜索算法(ConnBC)进行了比较，主要是通过比较所有算法在协作伙伴选择时遍历的候选节点个数，当遍历候选节点数越少，表明其算法更优.实验4与实验3采用了同样的数据选取方法，如图14所示.其中，基于网络划分的任务协作者搜索算法是用实线线条表示，具有更好的性能，而且，随着专家候选者数据量的不断增大，表现更加明显.

实验5. 社会工作流任务分派算法的正确性验证.

支持社会协同计算的跨组织工作流任务分派方法通过将跨组织工作流任务外包到候选者社会网络中，从候选者网络中查找到领导者节点及任务协作伙伴，并保证协同交互成本最低.通过比较Kargar和An[6]提出的BruteForce算法，Juang等人[7]提出BCPruning算法和SSPruning算法，及所提算法(Proposed)，验证了所提算法的正确性，如图15所示.其中，Proposed算法是用实线条表示，其交互成本几乎与BruteForce接近，表明Proposed算法能够选出关系密切的专家服务组合.

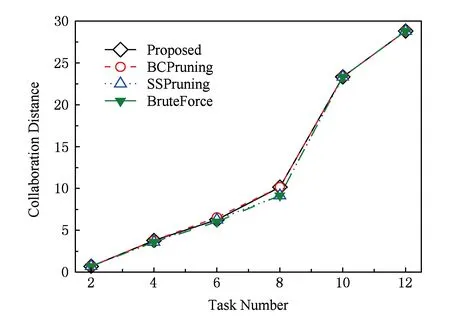
Fig. 15 Correctness verification of social workflow task allocation图15 社会工作流的任务分派算法正确性验证

实验结果表明本文所提出的跨组织工作流任务分派算法，大幅降低了工作流任务分派的时间成本，并能保持较高的算法精度，适用于大规模社会网络的协同计算问题.但存在2点不足：1)算法结果还不够精确，应更进一步提高；2)当工作流任务子网连接点数目很多时，所提算法的时间效率仍会不理想，应设计出不同的应对解决方案.

5 结 论

复杂社会网络所固有的大规模性特征给支持社会协同计算应用的算法性能提出了更高的要求.针对面向大规模社会网络的跨组织工作流人工任务分派问题，提出了一种支持社会协同计算的跨组织工作流分派优化算法，采用了基于工作流任务子网的分层优化思想，有效地划分复杂社会网络图，简化了最短路径的近似计算问题；并依据划分后人工服务社会网络的拓扑特征，改进了快速介数中心性算法，设计了一种新颖的基于任务子网连接点的快速介数中心性计算方法，高效地选取跨组织业务项目的领导者；然后，采用基于任务子网划分的最短路径近似算法，实现了快速查找跨组织业务项目的协作成员；理论证明和仿真实验表明所提出分派方法具有良好的算法性能，并保持较高的算法精度，有效地解决了跨组织工作流任务成员之间的关系评价和人工服务组合优化的时效性问题，适用于复杂的大规模社会网络协同计算.

[1]Skopik F, Schall D, Dustdar S, et al. Modeling and mining of dynamic trust in complex service-oriented systems[J]. Information Systems, 2010, 35(7): 735-757

[2]Schall D, Satzger B, Psaier H. Crowdsourcing tasks to social networks in BPEL4People[J]. World Wide Web-Internet and Web Information Systems, 2014, 17(1): 1-32

[3]Feng Jianhong, Li Guoliang, Feng Jianhua. A survey on crowdsourcing[J]. Chinese Journal of Computers, 2015, 38(9): 1713-1726 (in Chinese)(冯剑红, 李国良, 冯建华. 众包技术研究综述[J]. 计算机学报, 2015, 38(9): 1713-1726 )

[4]Kittur A, Nickerson J V, Michael S B. The future of crowd work[C]Proc of ACM Int Conf on Computer Supported Cooperative Work. New York: ACM, 2013: 1301-1318

[5]Gradiraju U, Demartini G D, Kawase R, et al. Human beyond the machine: Challenges and opportunities of microtask crowdsourcing[J]. IEEE Intelligent Systems, 2015, 30(4): 81-85

[6]Kargar M, An A. Discovering top-kteams of experts withwithout a leader in social networks[C]Proc of the 20th ACM Int Conf on Information and Knowledge Management. New York: ACM, 2011: 985-994

[7]Juang Mingchin, Huang Chenche, Huang Jiunlong. Efficient algorithms for team formation with a leader in social networks[J]. Journal of Supercomputing, 2013, 66(2): 721-737

[8]Wang Xinyu, Zhao Zhou, Ng W. USTF: A unified system for team formation[J]. IEEE Trans on Big Data, 2016, 2(1): 70-84

[9]Yu Yan, Wang Ying, Liu Xingmei, et al. Workflow task assignment strategy based on social context[J]. Journal of Software, 2015, 26(3): 562-573 (in Chinese)(余阳, 王颍, 刘醒梅, 等. 基于社会关系的工作流任务分派策略研究[J]. 软件学报, 2015, 26(3): 562-573

[10]Gorge S, Bergmann R. Social workflows—Vision and potential study[J]. Information Systems, 2015, 50(1): 1-19

[11]Dorn C, Taylor R N, Dustdar S. Flexible social workflows: Collaborations as human architecture[J]. IEEE Internet Computing, 2012, 16(2): 72-77

[12]Tang Jintao, Wang Ting, Wang Ji. Shortest path approximate algorithm for complex network analysis[J]. Journal of Software, 2011, 22(10): 2279-2290 (in Chinese)(唐晋韬, 王挺, 王戟. 适合复杂网络分析的最短路径近似算法[J]. 软件学报, 2011, 22(10): 2279-2290)

[13]Sun Huanliang, Jin Mingyu, Liu Junling, et al. Methods for team formation problem with grouping task in social networks[J]. Journal of Computer Research and Development, 2015, 52(11): 2535-2544 (in Chinese)(孙焕良, 金洺宇, 刘俊岭, 等. 社会网络上支持任务分组的团队形成方法[J]. 计算机研究与发展, 2015, 52(11): 2535-2544)

[14]Gubichev A, Bedathur S, Seufert S, et al. Fast and accurate estimation of shortest paths in large graphs[C]Proc of the 19th ACM Int Conf on Information and Knowledge Management. New York: ACM, 2010: 499-508

[15]Tretyakov K, Armascervantes A, Garciabanuelos L, et al. Fast fully dynamic landmark-based estimation of shortest path distances in very large graphs[C]Proc of the 20th ACM Int Conf on Information and Knowledge Management. New York: ACM, 2011: 1785-1794

[16]Qiao Miao, Cheng Hong, Chang Lijun, et al. Approximate shortest distance computing: A query-dependent local landmark scheme[J]. IEEE Trans on Knowledge and Data Engineering, 2014, 26(1): 55-68

[17]Freeman L. A set of measures of centrality based upon betweenness[J]. Stoichiometry, 1977, 40(1): 35-41

[18]Brandes U. A faster algorithm for betweenness centrality[J]. Journal of Mathematical Sociology, 2001, 25(2): 163-177

[19]Kolaczyk E D, Chua D B, Barthelemy M. Group between-ness and co-betweenness: Inter-related notions of coalition centrality[J]. Social Networks, 2009, 31(3): 190-203

[20]Meng Xiaofeng, Li Yong, Zhu Jianhua. Social computing in the era of big data: Opportunities and challenges[J]. Journal of Computer Research and Developent, 2013, 50(12): 2483-2491 (in Chinese)(孟小峰, 李勇, 祝建华. 社会计算: 大数据时代的机遇与挑战[J]. 计算机研究与发展, 2013, 50(12): 2483-2491)

[21]Kucherbaev P, Daniel F, Tranquillini S, et al. Crowdsourcing processes: A survey of approaches and opportunities[J]. IEEE Internet Computing, 2016, 20(2): 50-56

Sun Yong, born in 1977. PhD. Lecturer. Member of CCF. His main research interests include cooperative computing, service computing, social workflow scheduling, intelligent infor-mation systems and software engineering.

Tan Wenan, born in 1965. PhD, professor, PhD supervisor. Senior member of CCF. His main research interests include soft-ware engineering, process engineering and development environment, enterprise dynamic modeling, trusted service computation and enterprise intelligent information systems.

Cross-Organizational Workflow Task Allocation Algorithms for Socially Aware Collaborative Computing

Sun Yong1and Tan Wenan1,2

1(SchoolofComputerScienceandTechnology,NanjingUniversityofAeronauticsandAstronautics,Nanjing211106)2(CollegeofComputerandInformation,ShanghaiPolytechnicUniversity,Shanghai201209)

Recently, human-interactions are substantial part of Web service-oriented collaborations and cross-organizational business processes. Social networks can help to process crowdsourced workflow tasks among humans in a more effective manner. However, it is challenging to identify a group of prosperous collaborative partners with a leader to work on joint cross-organizational workflow tasks in a prompt and efficient way, especially when the number of alternative candidates is large in collaborative networks. Therefore, in this paper, a new and efficient algorithm has been proposed to find an optimal group in social networks so as to process crowdsourced workflow tasks. Firstly, a set of new concepts has been defined to remodel the social graph; then, a sub-graph connector-based betweenness centrality algorithm has been enhanced to efficiently identify the leader who serves as the host manager of the joint workflow tasks; finally, an efficient algorithm is proposed to find the workflow task members associated with the selected leader by confining the searching space in the set of connector nodes. Theoretical analysis and extensive experiments are conducted for validation purpose; and the experimental results on real data show that our algorithms outperform several existing algorithms in terms of computation time in dealing with the increasing number of workflow task executing candidates.

collaborative computing; team formation; task allocation; cross-organizational workflow; social network

2016-07-13；

2016-12-28

国家自然科学基金项目(61672022,61272036);安徽省高校自然科学基金重点项目(KJ2017A414) This work was supported by the National Natural Science Foundation of China (61672022, 61272036) and the Key Project of University Natural Science Foundation of Anhui Province (KJ2017A414).

TP391.1