基于对齐的BPMN 2.0模型符合性检测算法

汪玉泉 闻立杰 闫志强

1(清华大学软件学院 北京 100084)2 (首都经济贸易大学信息学院 北京 100070)

基于对齐的BPMN 2.0模型符合性检测算法

汪玉泉1闻立杰1闫志强2

1(清华大学软件学院 北京 100084)2(首都经济贸易大学信息学院 北京 100070)

(272269222@qq.com)

符合性检测方法作为比较和关联事件日志与流程模型的技术，是三大核心流程挖掘技术之一，可用于量化符合性和诊断偏差.BPMN 2.0模型具有丰富的表达能力，能够表达多实例、子流程、边界事件、OR网关等多种复杂模式，但是目前还没有针对这些复杂模式的BPMN 2.0模型符合性检测算法.针对该问题，提出了基于对齐的BPMN 2.0模型符合性检测算法Acorn，该算法支持上述多种复杂模式.在深入分析BPMN 2.0模型中多种复杂模式的具体语义并分析其具体使能情况的基础上，Acorn算法引入对齐操作，利用A*搜索算法寻找到代价最小的匹配轨迹，同时引入虚拟代价和预估代价来对A*算法进行搜索空间的优化，最后根据最佳匹配轨迹来计算模型与日志的契合度.实验表明，Acorn算法能够正确有效地计算带有复杂模式的BPMN 2.0模型与日志之间的契合度，且虚拟代价和预估代价的引入，大大减少了搜索空间，有效提高了算法的运行速度.

BPMN 2.0模型；复杂模式；A*搜索；符合性检测；对齐

工作流技术在最近十几年得到了迅速的发展，该技术通过对日常工作中固定程序活动进行抽象，将工作分解成定义良好的任务或者角色工作，按照一定的规则和流程来执行这些任务并对其进行监控，达到提高工作效率、更好地控制流程、增强对客户的服务、有效管理业务流程等目的[1].

BPMN(business process model and notation)[2]是由BPMI(Business Process Management Initiative)开发的一套标准的业务流程建模符号.BPMN 2.0规范于2011年正式发布，相比于2004年提出的BPMN 1.0规范有了巨大的改进，多实例、子流程、边界事件等多种元素的引入，极大地丰富了BPMN 2.0模型的表达能力.BPMN 2.0模型符号容易被业务分析员理解和使用，现已成为当前最流行的业务流程可视化描述语言.

符合性检测是工作流技术中非常重要的模块.符合性检测是用来检测流程模型和日志之间匹配程度的技术，即该模型能在多大程度上反映出该日志相关流程执行过程的本质.通常企业在初始阶段没有进行系统地建模，但在其系统中仍记录了大量的活动执行过程.在企业规模逐渐扩大、业务逐渐复杂之后，企业通常通过一些自动挖掘技术，在大量实际日志的基础上挖掘出工作流模型来更好地管理业务[3-5]，从而提高工作效率，但我们往往需要符合性检测来衡量挖掘出来的模型的质量.此外，当流程模型执行产生的流程日志与原始模型偏差较大，即二者的符合性低于给定阈值时，有必要对原始模型进行修复操作[6].

然而目前的符合性检测技术大都集中在Petri网[7]上，很少有针对BPMN模型的符合性检测，即便有也是只考虑了BPMN模型中的活动和网关[8]，并没有考虑到BPMN 2.0标准中的多实例、子流程、边界事件等特殊元素的存在和影响.多实例、子流程和边界事件等复杂模式的存在，大大增加了符合性检测算法的设计难度.

BPMN 2.0模型的符合性检测算法具有如下3个难点：

1) 多实例、子流程的存在，使得模型可以对应无穷多个实例轨迹，直接计算匹配程度较为困难；

2) OR网关的不对称存在，使得OR网关的使能情况异常复杂；

3) 边界事件和多实例的存在，使得多种事件可以同时使能，但相互之间是冲突的，需要根据具体情况进行分析.

本文致力于在考虑BPMN 2.0标准中的多实例、子流程、边界事件等特殊元素的基础上，研究BPMN 2.0模型和已有日志的符合性检测工作，主要贡献如下：

1) 针对多实例、子流程、边界事件等每种特殊元素，进行其语义分析；

2) 设计对齐算法，寻找BPMN 2.0模型上可执行的1条轨迹，使其转换成已有轨迹所需的代价最小；

3) 提出Acorn算法，用于衡量BPMN 2.0模型和日志之间的契合度.

1 相关工作

符合性检测主要用于检测模型能在多大程度上来描述已有日志的行为，目前比较公认的流程模型和日志之间符合性检测的衡量指标主要有4种：

1) 契合度(fitness).用于衡量有多少日志中的行为被模型所支持.

2) 准确率(precision).用于衡量有多少模型上的行为被日志所支持.

3) 一般性(generalization).用于衡量模型解析日志之外行为的能力，如用90%的日志挖掘出来的模型，能很好地解析剩下的10%的日志行为，就可以说该模型具有良好的一般性.

4) 复杂性(complexity).用于衡量模型的复杂程度，通常而言，在有同样的表达能力的前提下，用户往往希望模型是简单易懂的.

把同时出现在模型和日志中的行为称为“TruePositive”，出现在模型中但不出现在日志中的行为称为“FalsePositive”，反之只出现在日志中但不出现在模型中的行为称为“FalseNegative”，通常：

(1)

(2)

Molka等人[8]针对BPMN模型提出了计算召回率和准确率的符合性检测算法.该文定义了“局部行为”和“全局行为”，并设计算法在模型和日志中抽取这2种行为，从而进一步计算召回率和准确率.然而该算法针对的BPMN模型仍停留在BPMN 1.0时代，并未包含BPMN 2.0模型中的多实例、子流程、边界事件等各种特殊元素，故应用场景比较有限.

Adriansyah等人[9]提出了若干个关于契合度方面的衡量指标，针对每条轨迹t1，作者通过A*算法寻找到模型上的最优的1条轨迹t2，且要保证t2是t1的子集，由此可以计算出轨迹t1中不能被模型解析的部分，从而进一步来计算契合度指标.

de Leoni等人[10]针对声明式(declarative)模型[11]提出基于对齐的符合性检测算法.基于对齐的算法假设模型和日志都可以保持自身不变，等待对方强制执行某流程，从而越过不匹配的活动，同时记录不匹配活动的代价，通过A*搜索算法来寻找到代价最小的1条对齐轨迹.然而，声明式模型与BPMN 2.0模型存在显式差别，且未见BPMN 2.0模型到声明式模型的转换工作.因此，本文无法直接使用文献[10]的研究成果.

vanden Broucke等人[12]通过引入负事件(nega-tive event)，从全新的角度来衡量模型与日志之间的准确度和模型的一般性.通过对日志的全局分析，即可计算出每条轨迹中每个活动对应的负事件.随后让每条轨迹在模型上一步步执行，每执行1步即可得到该步之后有哪些使能的活动属于负事件或者正事件(positive event)，并将相应的结果计算入最终的准确度和一般性结果中.但由于该方法在某活动不能在模型上执行的情况下采取的是强制执行的方法，适合于大部分模型，但却不适合BPMN 2.0模型，因为BPMN 2.0模型中包含多实例的活动和子流程，若某活动或子流程需要被强制执行，但是它被标记为多实例，即有多个活动或子流程实例，那么强制执行哪个实例仍是未知的问题，强制执行不同的实例会导致不同的计算结果.

契合度是4个指标最为重要的衡量指标.由于负事件的应用在BPMN 2.0模型中有上述局限性，故本文主要关注BPMN 2.0与日志之间契合度的衡量.与文献[10]中的方法相似，本文通过对BPMN 2.0模型的深入理解，设计基于对齐的算法，通过A*算法寻找到代价最小的匹配轨迹，进一步计算契合度.

2 Acorn算法设计

2.1 BPMN 2.0模型元素含义

BPMN 2.0定义了规范的执行语义和格式，利用标准的图元来描述现实的流程，从而保证即便在不同的流程引擎下得到的执行结果也是一样的.其模型定义如下：

定义1. BPMN 2.0模型.BPMN 2.0模型为一个四元组M=(A,G,E,S)，其中：A表示“Activity”，表示在流程图中具备声明周期状态的元素，包含原子级的任务(task)和子流程(sub-process)；G表示“Gateway”，主要包含XOR网关、OR网关和AND网关；E表示“Event”，利用事件机制，为系统增加辅助功能，主要包含启动(start event)、结束(end event)和中间事件(intermediate event)等；S表示“Sequence”，主要为流向(sequence flow).

BPMN 2.0规范支持的元素异常之多，表1列举了本文算法中支持的各种BPMN 2.0元素及该元素的执行语义.

2.2 BPMN 2.0模型元素使能分析

对于任务来说，只要有输入流到达，则该任务就是使能的，然而BPMN 2.0模型中包含了很多特殊元素，需要逐一考虑.

1) XOR网关.XOR网关分为2种，即XOR-SPLIT网关和XOR-MERGE网关.XOR-SPLIT表示选择开始，XOR-MERGE表示选择结束.根据表1中的语义，XOR网关表示只有1条分支能够执行，故遇到XOR-SPLIT网关，假设其有n条流出的序列流，则可以产生n种不同的使能状态，每条分支为1种状态.遇到XOR-MERGE则直接使能该网关，因为任意1条输入的序列流都可以使能该网关.

2) AND网关.AND网关分为2种，即AND-SPLIT网关和AND-MERGE网关.AND-SPLIT网关表示并发的开始，则其输出序列流对应的活动都应该使能；AND-MERGE网关则表示并发的结束，需要所有分支都已经执行完，故对每个AND-MERGE网关，需要记录该网关哪些流入的序列流已经使能.

Table 1 BPMN 2.0 Elements and Their Execution Semantics

3) OR网关.OR网关同样分为OR-SPLIT网关和OR-MERGE网关.根据表1的语义，OR-SPLIT后可以有若干个(至少1个)分支被使能，假设该网关有n个流出向的序列流，则有2n-1种对应的使能状态；OR-MERGE则相对来说复杂一些，并不像XOR-MERGE和AND-MERGE那样有规则，而是需要根据前面OR-SPLIT的情况来定.图1展示了2种不同的OR-MERGE情况，图1(a)展示了一种规则的情况，即OR-MERGE网关与OR-SPLIT一一对应;而图1(b)则展示了一种不规则的情况，即可以有n个OR-MERGE和m个OR-SPLIT对应.鉴于有存在图1(b)展示的情况，判断OR-MERGE是否使能显得有些复杂.需要按照以下步骤来进行：

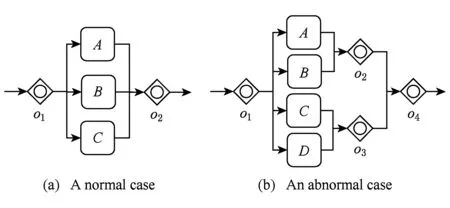
Fig.1 A sample for OR-SPLIT图1 OR-SPLIT示例

① 预处理BPMN 2.0模型中每个元素能到达的OR-MERGE网关，本文用R(x)表示x元素能够到达的OR-MERGE网关，在图1(b)中，任务A和B能够到达的OR-MERGE为o2和o4，即R(A)=R(B)={o2,o4}，C和D能够到达的OR-MERGE为o3和o4，即R(C)=R(D)={o3,o4}.

② 每使能1个任务，则更新该任务能够到达的OR-MERGE网关，表明该活动使能，则这些OR-MERGE网关需要等到这个任务执行完后才能使能，即每使能任务x，需要更新∀o∈R(x),o.waitingList.add(x)，其中waitingList为2.3节中间状态的变量之一，表示该OR-MERGE网关需要等待的任务集合.在图1(b)中，若o1网关后使能的是A和D，则更新o2，o4需要等待A的执行，更新o3，o4需要等待D的执行，即o2.waitingList={A},o3.waitingList={D},o4.waitingList={A,D}.

③ 每执行完1个任务，则更新该任务对应的所有OR-MERGE网关，告诉该网关不必继续等待该任务，即每执行任务x，需要更新∀o∈R(x),o.waitingList.remove(x)，其中waitingList表示该OR-MERGE网关需要等待的任务集合.图1(b)中，任务A执行后，则o2，o4进行更新，更新之后o2不必再等待任何活动，而o4还需要等待任务D的执行，即o2.waitingList={},o4.waitingList={D}.

④ 当访问到OR-MERGE网关时，若该网关不需要等待任何任务，则该网关使能，即若该OR-MERGE网关的waitingList为空，则该网关使能，反之则不使能.图1(b)中，续上面的例子，任务A执行后，o2.waitingList={}，即o2不需要等待任何任务，则使能，而o3，o4都需要等待D的执行，则不使能.

4) 子流程.每次使能1个子流程，则使能该子流程中的开始事件.每次执行完子流程中的结束事件后，则跳出该子流程.

5) 多实例.多实例表明该任务或者子流程可以发生多次，故需要用实例编号来区分各个实例.当某个任务体现出多实例的特性时，第1个实例给予编号“_1”，第2个实例给予编号“_2”，若有多层的多实例，如子流程被标记为多实例，且其中的任务也被标记为多实例，则可以采用“_1_1”，“_1_2”的形式来进行区分，当多实例结束时，则修改成上层的实例编号.本文默认，存储在优先队列中的任务都带有实例编号.

6) 边界事件.包括取消事件、定时事件和错误事件.这3种事件的语义表现基本一致，只是产生事件的原因不同.若任务或者子流程包含这些事件，则这些事件对应的分支随时是使能的.

2.3 基于对齐的匹配算法

定义3. 日志.日志L={T1,T2,…,Ti,…,Tn}，其中Ti表示第i条轨迹.

基于对齐的模型与日志匹配算法，其本质是在模型上逐条重演相应日志的轨迹，即模型中任务依据规则逐个执行的同时，轨迹中对应任务进行逐个遍历输出.往往1条轨迹中的所有任务不能完美地在模型上按照次序重演下来，故需要引入对齐的概念.引入“≫”标识符，表示用来对齐，并不执行真正的具体任务.

定义4. 对齐.假定s′为模型中依据规则执行的当前任务，s″为轨迹中按序遍历输出的当前任务，则(s′,s″)是模型和轨迹的1次对齐，其中：

1) 若s′为模型中的任务而s″=≫，则该对齐仅为模型中s′的执行，而轨迹未动；

2) 若s′=≫而s″为轨迹中的任务，则该对齐仅为轨迹中s″的输出，而模型未动；

3) 若s′=s″≠≫，则该对齐表示模型中s′执行的同时，对轨迹中s″进行输出.

例1. 图2表示已有的BPMN2.0模型，整个流程先执行A任务，之后D任务和1个子流程并发执行，该子流程在执行若干个B任务实例后执行C任务，该子流程可以同时产生多个实例，待并发结束后，最后执行E任务.现在已有轨迹t=A,C,E，需要通过重演在模型上找1条匹配轨迹.图3展示了4种轨迹在模型上重演的对齐方案.

Fig. 2 A sample for BPMN 2.0 model图2 BPMN 2.0模型示例

Fig. 3 Several alignments between the trace and the model in example 1图3 例1轨迹与模型的若干种对齐方案

轨迹在模型上重演，可以产生非常多的对齐方案.需要找到和轨迹最为相似的那种重演方式，很明显，Y1是需要的那种对齐方式，因为Y1中只引入了2次“≫”，只有任务B和D没有找到相匹配的，任务A，C，E均完成了匹配.

定义下面的代价函数，可以用来评估对齐方案Y的好坏，其中单个对齐代价的具体值用户可以自定义：

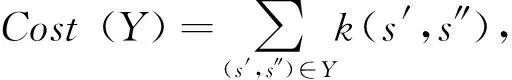
(3)

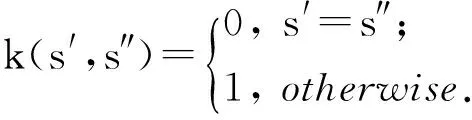
由该代价函数易知，Y1的对齐方案的代价为2，Y3的对齐方案的代价为3，而Y2和Y4的对齐方案的代价为4，故Y1是最优的对齐方案.基于对齐的轨迹与模型的匹配方案，即寻找代价最小的对齐方案.

存在子流程可能会被标记成多实例的情况，每次使能1个子流程的实例，都只是简单地启动该子流程的开始事件，而事件这种元素并不会记录在最终的日志中，故事件不会累计在最终的代价里.如此一来，就会产生一个问题，队列是按照代价大小排序的，而子流程可能产生无数个实例且代价不变(假设每个实例都只是启动开始事件)，将会导致算法陷入死循环，故在此引入真实代价和虚拟代价的概念.

真实代价是引入对齐符号“≫”所产生的代价，即模型和轨迹某个活动没有匹配上产生的代价；而虚拟代价是启动子流程实例产生的代价，每次启动1个子流程的开始事件，标记1次虚拟代价，即虚拟代价总和加1.

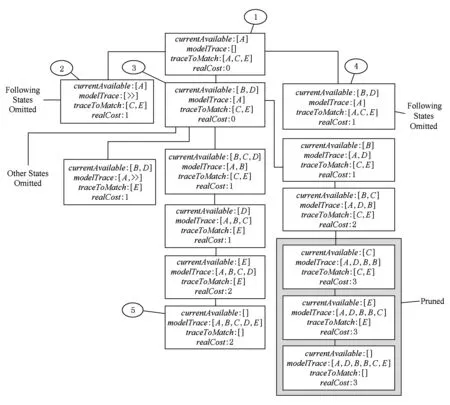
Fig.4 The core idea of finding the optimal alignment for example 1 using A* search algorithm图4 例1使用A*搜索算法寻找最佳匹配示意

本文采用A*搜索算法来寻找基于对齐的最佳匹配，整体思路是通过优先队列，维护一系列的匹配中间状态，每次挑选最小代价的中间状态，在其基础上继续重演，直到找到总体代价最小的匹配.优先队列维护的中间状态如定义5所示.

定义5. 中间状态.优先队列中维护着一系列的匹配中间状态，每个状态包括多个中间变量：

1)currentAvailable，类型为HashSetTask，记录目前所有已经使能的任务.

2)parallelSync，类型为HashMapTask,HashSetSequenceFlow，键为AND-MERGE网关，值为该网关流入的序列流，用来标记哪些入口已经使能，当所有入口均已使能，则该AND-MERGE网关使能.

3)waitingList，类型为HashMapTask,HashSetTask，键为OR-MERGE网关，值为该网关需要等待执行的任务，当该网关需要等待的任务数为0时，该OR-MERGE网关使能.

4)modelTrace，类型为ListString，记录模型上的轨迹，包括任务名字和对齐标志“≫”.

5)traceToMatch，类型为ListString，记录还需等待匹配的轨迹.

6)cost，分为totalCost，realCost，virtualCost和expectedCost，每种类型均为Int.totalCost为后面3种代价之和，优先队列中按totalCost从小到大排序；realCost记录当前状态下的真实代价，每增加1个对齐标志“≫”，代价加1；virtualCost为引入子流程开始事件的代价；expectedCost为当前状态到匹配结束状态的估算代价，在2.4节会具体介绍.

图4展示了例1中A*搜索算法的具体执行过程，最初始有一个状态如节点1所示，节点1表示当前状态下模型上只有A是使能的，模型上的执行轨迹暂为空，待匹配的轨迹为A,C,E，代价为0，随后状态2，3，4则是根据上述规则所衍生出的下一系列中间状态：状态2表明模型上不执行任务但待匹配轨迹上执行任务A，引入了对齐操作，故代价为1；状态3表明模型与待匹配轨迹均执行任务A，没有引入对齐操作，故代价仍保持为0；状态4则是与状态2相反，模型上执行任务A但待匹配轨迹不执行，即待匹配轨迹上引入了对齐操作，故代价也变成1.之后状态2，3，4也根据如上规则继续进行状态的演变，由于篇幅限制，图4中省略了很多的中间状态只展示了关键的若干中间变量，集中表现了其中代价为2和代价为3的对齐情况的具体衍生过程.根据A*算法的剪枝规则，在已经得到代价为2的对齐方案(状态5)后，图中带有灰度的部分将会被剪枝，不会真正被一步步执行，以此来减少计算量.

假设当前轨迹为tr，通过A*搜索算法找到代价最小的匹配轨迹为match_trace，便可对该条轨迹的契合度进行计算[13](其中cost为算法得到的最小代价，len(tr)和len(match_trace)为2条轨迹的长度)，而整个日志和模型的契合度则可以看成是所有轨迹契合度的平均，分别见式(4)和式(5).

(4)

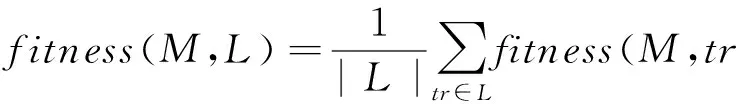
(5)

2.4 A*搜索算法优化

A*搜索算法的代价函数为f(x)=g(x)+h(x).其中，g(x)为当前已有代价，为真实代价与虚拟代价之和；h(x)为启发式的预估当前状态到结束状态所需的代价，即中间状态中的预估代价.

本节主要讨论h(x)预估代价的计算.多实例的存在，使得轨迹可以无限变长，而边界事件的存在，使得子流程又可以中途结束，故很多情况下很难预估当前状态到结束状态所需的代价.有种情况例外，即模型上使能了多个子流程的开始事件，若执行完所有子流程得到的最短轨迹长度已经大于待匹配轨迹长度，则两者差的绝对值便为预估代价.

例2. 图2表示已有的BPMN 2.0模型，假设当前状态中的modelTrace为A，并且使能了2次包含B活动的子流程的开始事件，traceToMatch为E，说明模型上已经执行了任务A，且将要执行2次子流程，而待匹配的轨迹为任务E，可以看到，执行2次子流程最少需要4步(如B,C,B,C)，而待匹配的轨迹仅为E，故至少需要|B,C,B,C|-|E|=3次对齐的代价来完成匹配.

针对此种情况，可以对模型进行预处理，根据BPMN 2.0元素的语义，计算出每个开始事件到该子流程结束状态的最短轨迹长度，在计算中间状态时，若发现执行已使能的子流程所需要最短轨迹长度大于待匹配的轨迹长度，则可以把该长度差计入预估代价中.

需要注意的是，以上通过对子流程代价的预估，来进行搜索空间的剪枝是必须的，而不是可选的.因为子流程多实例的特性，语义上可以产生无数个子流程，尽管已经使用虚拟代价使得子流程多的中间状态优先级降低，但是在计算真实代价的时候，不会将虚拟代价计算入内，仍会导致无数个中间状态.大部分情况下，通过对子流程代价的预估，往往限定了子流程的使能次数，可以大大减少搜索空间，然而若该子流程的任何一个父流程标有取消、错误等事件，说明使能的若干个子流程随时可以退出，则对子流程的预估便会变得无效，因为这些子流程不是必须完整执行的了.在此种情况下，可以设定子流程多实例的上限阈值，即最多可以同时使能多少个子流程，而这同时也是符合实际情况的，一个事件或者流程不可能无限制地被执行.

3 Acorn算法实现

本文采用A*搜索算法来寻找基于轨迹对齐的最佳匹配.如算法1所示:

算法1. 单条轨迹与流程模型最佳对齐算法(BestBPMN2.0Alignment).

输入：单条轨迹trace、BPMN 2.0模型model；

输出：最小代价cost、对齐后轨迹match_trace.

① 令q为一个保存按照totalCost由低到高排序的中间状态的优先队列；

② 令cost为当前最小的realCost,初始化为INT_MAX;

③ Whileqis not empty do

④ 令s为具有最小totalCost的当前状态;

⑤ Ifs.currentAvailableis NULL ors.traceToMatchis NULL do

⑥ updatecostandmatch_trace; continue;

⑦ End If

⑧ Ifs.realCost≥costdo continue;

⑨ End If

⑩ Foreach tasktins.currentAvailabledo

每次循环，算法1都从队列中取出当前代价最小的中间状态(行④)，并进行状态的演变.

算法1的行⑤～⑦处理状态不能再继续演变的情况，即模型上已经走到尽头(没有使能的任务)或者轨迹已经全部匹配完的情况.如果是模型已经匹配完的情况下，则s的代价需要加上未匹配轨迹的长度当成额外的代价，而如果是轨迹已经全部匹配完，则根据当前状态计算模型上离结束所需的最小步数，并将其计入代价中.行⑧～⑨ 用来剪枝，排除代价已经高于目前最小值的中间状态.

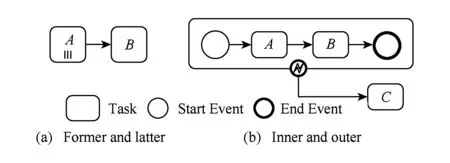
Fig. 5 Two samples for conflicts between enabled tasks图5 使能任务的2种冲突示例

图5(a)展示了前后冲突，当任务A执行完后，使能的任务有A和B，当选择任务B来执行时，说明任务A的多实例已经结束，故需要在已经使能的任务列表中删除任务A的实例.图5(b)则展示了内外冲突，当任务A执行完后，任务B使能，同时由于该子流程标记着边界事件，任务C也使能，当接下来选择C来执行时，则说明子流程通过边界事件跳出，则B任务不应该再使能.

1) 模型执行当前任务，产生一系列的后继状态，而轨迹则保持不变，即轨迹上执行对齐“≫”.该行为仅为模型上的1次移动，代价需要在原先基础上加1，如图4中状态1到状态4的转变.

2) 模型执行当前任务，产生一系列的后继状态，且轨迹中第1个任务与模型当前任务相同，则轨迹也执行该任务，且更新轨迹(去除轨迹中第1个任务).该行为为模型与轨迹的同时移动，代价不变，如图4中状态1到状态3的转变.

3) 模型不执行任务，而轨迹则执行当前第1个任务，即模型上执行对齐“≫”.该行为仅为轨迹上的1次移动，代价需要在原先基础上加1，如图4中状态1到状态2的转变.

需要注意的是，在进行对齐产生新状态的时候，需要更新中间状态中的所有中间变量.

Acorn算法的实现如算法2所示.对日志中的每条轨迹均用其最佳匹配进行契合度计算，最后取其均值作为日志与模型的契合度.

算法2. 流程日志与流程模型的契合度算法(Acorn).

输入：流程日志L、BPMN 2.0模型model；

输出：流程日志与流程模型的契合度.

① 令f为契合度，初始化为0;

② Foreach tracetinLdo

③cost,match_trace=BestBPMN2.0-Alignment(t,model);

④f+=fitness(model,t);

⑤ End For

⑥f=|L|;

⑦ Returnf.

4 实验评估

4.1 实验设置

所有实验均在笔记本电脑上完成，其配置为：酷睿2双核处理器，T7500 CPU (2.2 GHz,800 MHz FSB,4 MB L2 cache)，内存为4 GB，操作系统为Windows 7,JDK为1.6版本.

实验用的BPMN 2.0模型来自国内某大型通信公司，均由专业人员建模形成.对每个BPMN 2.0模型，使用课题组自主研发的模型仿真工具来产生一系列的日志，再随机对日志中轨迹进行增删改操作，如遍历每条轨迹并对每个活动随机应用以下任意一种操作：1)在该活动前添加1个活动；2)修改该活动的名称；3)删除该活动；4)保持不变.然后，对模型与日志应用Acorn算法来计算契合度，把得到的结果与专家人工进行最优匹配的结果进行对比，以此确保算法的正确性.

4.2 效果评估

本实验使用多个模型来验证算法契合度计算的正确性，每个模型的特征如表2所示.根据引言所述，基于对齐的BPMN 2.0模型符合性检测算法主要针对多实例、OR网关、子流程、边界事件等特殊属性，故表2枚举了每个BPMN 2.0模型所包含的特殊属性.

可以看到，所有特殊属性均包括在测试用例中，包括特殊属性之间的混合搭配.在效果评估试验中，Acorn算法得到的结果与专家人工进行最优匹配的结果完全一致，这归功于Acorn算法采用了A*搜索算法来寻找基于轨迹对齐的最佳匹配.

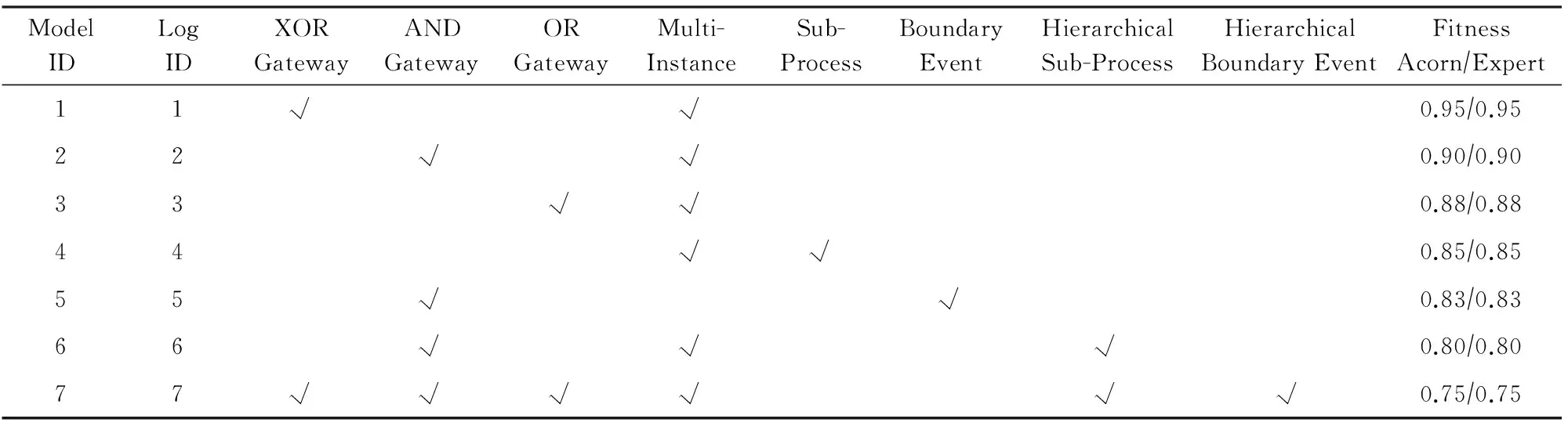
Table 2 The Structural Features and Conformance of Process Models and Logs for Effectiveness Testing Experiments

4.3 性能评估

表3展示了Acorn算法在不同日志规模输入下的性能表现，其中日志8_1和8_2，9_1和9_2，10_1和10_2分别对应模型8，9，10，该结果表明在正常规模下的模型与日志来进行符合性算法检测，其耗时均在可接受范围内.日志8_1和8_2的对比表明，相同模型下带匹配轨迹长度越长，耗时越长.同样，日志9_1和9_2，日志10_1和10_2的对比也能得出该结论.日志9_1，9_2与日志10_1，10_2对应的实验结果表明，模型的复杂程度同样影响算法运行时间，一般模型越复杂，耗时越多.实验结果中可以看到，含有OR网关或者多实例子流程的模型，往往需要更多的匹配时间.原因也较好理解，这2种元素均会产生多个临近的中间状态，故BPMN 2.0模型中包含的特殊元素是影响其运行时间的重要因子之一.

Table 3 The Performance of Acorn Algorithm on Process Models with Different Sizes

4.4 优化评估

表4展示了针对同一个包含若干多实例和嵌套多实例的过程模型和其对应日志，在不同多实例阈值下Acorn算法进行契合度计算时需要访问的中间状态的数量.可以看到，在不做任何优化的前提下，随着阈值的增加，很快便出现状态爆炸的情况，虚拟代价和预估代价的引入均能在一定程度上进行有效的剪枝，而两者的结合则是大大提升了算法的剪枝能力，避免了很多无用状态的访问.需要注意的是，在使用虚拟代价+预估代价的情况下，无论多实例阈值如何，节点搜索过程始终按照最优路径行进，而没有访问多余的中间状态，因此在3种不同多实例阈值的情况下，Acorn算法访问的中间状态数量相同.

Table 4 Comparison of the Number of Intermediate States Accessed Under Various Costs in Different

5 总结与展望

本文提出了基于BPMN 2.0模型的符合性检测算法Acorn.特殊网关、多实例、子流程、边界事件等的存在，使得BPMN 2.0模型的符合性检测变得比较困难，通过对这些特殊元素的语义的深入研究，且引入对齐操作，通过A*算法来搜索代价最小的匹配轨迹，从而完成符合性检测分析.实验结果表明该算法能有效地支持多种BPMN 2.0特殊元素，且准确有效.

该算法尚存在一些不足.基于A*的搜索算法，在最坏情况下会遍历所有可能的匹配，故需要较长时间才能完成符合性检测，故之后的研究方向将会放在A*算法的优化方面.此外，将针对准确性[14-15]、一般性和复杂性等其他符合性指标继续开展研究工作.再者，考虑用多个不同维度的信息来计算契合度也是一大研究重点[16].

[1]Georgakopoulos D, Hornick M, Sheth A. An overview of workflow management: From process modeling to workflow automation infrastructure[J]. Distributed and Parallel Databases, 1995, 3(2): 119-153

[2]Chinosi M, Trombetta A. BPMN: An introduction to the standard[J]. Computer Standards & Interfaces, 2012, 34(1): 124-134

[3]van Dongen B F, de Medeiros A K A, Wen L. Process mining: Overview and outlook of Petri net discovery algorithms[G]LNCS 5460: Trans on Petri Nets and Other Models of Concurrency II. Berlin: Springer, 2009: 225-242

[4]Maggi F M, Bose R P J C, van der Aalst W M P. Efficient discovery of understandable declarative process models from event logs[C]Proc of Advanced Information Systems Engineering. Berlin: Springer, 2012: 270-285

[5]Wang Y, Wen L, Yan Z, et al. Discovering BPMN models with sub-processes and multi-instance markers[C]Proc of Conf on the Move to Meaningful Internet Systems (OTM 2015). Berlin: Springer, 2015: 185-201

[6]Polyvyanyy A, van der Aalst W M P, ter Hofstede A H M, et al. Impact-driven process model repair[J]. ACM Trans on Software Engineering and Methodology, 2017, 25(4): 1-60

[7]Murata T. Petri nets: Properties, analysis and applications[J]. Proceedings of the IEEE, 1989, 77(4): 541-580

[8]Molka T, Redlich D, Drobek M, et al. Conformance checking for BPMN-based process models[C]Proc of the 29th Annual ACM Symp on Applied Computing. New York: ACM, 2014: 1406-1413

[9]Adriansyah A, van Dongen B F, van der Aalst W M P. Towards robust conformance checking[C]Proc of Business Process Management Workshops. Berlin: Springer, 2010: 122-133

[10]de Leoni M, Maggi F M, van der Aalst W M P. Aligning event logs and declarative process models for conformance checking[C]Proc of the 10th Int Conf on Business Process Management (BPM 2012). Berlin: Springer, 2012: 82-97

[11]van der Aalst W M P, Pesic M, Schonenberg H. Declarative workflows: Balancing between flexibility and support[J]. Computer Science-Research and Development, 2009, 23(2): 99-113

[12]vanden Broucke S K L M, De Weerdt J, Vanthienen J, et al. Determining process model precision and generalization with weighted artificial negative events[J]. IEEE Trans on Knowledge and Data Engineering, 2014, 26(8): 1877-1889

[13]van der Aalst W M P, Adriansyah A, van Dongen B. Replaying history on process models for conformance checking and performance analysis[J]. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 2012, 2(2): 182-192

[14]Adriansyah A, Munoz-Gama J, Carmona J, et al. Measuring precision of modeled behavior[J]. Information Systems and E-Business Management, 2015, 13(1): 37-67

[15]Chatain T, Carmona J. Anti-alignments in conformance checking-The dark side of process models[C]Proc of Int Conf on Applications and Theory of Petri Nets and Concurrency. Berlin: Springer, 2016: 240-258

[16]Mannhardt F, de Leoni M, Reijers H A, et al. Balanced multi-perspective checking of process conformance[J]. Computing, 2016, 98(4): 407-437

Wang Yuquan, born in 1990. Master. His main research interests include process mining and conformance checking.

Wen Lijie, born in 1977. PhD, associate professor, PhD supervisor. His main research interests include process mining, process data management, workflow for big data analysis.

Yan Zhiqiang, born in 1983. PhD. Assistant professor. Member of CCF. His main research interests include process mining, process similarity and process repository.

Alignment Based Conformance Checking Algorithm for BPMN 2.0 Model

Wang Yuquan1, Wen Lijie1, and Yan Zhiqiang2

1(SchoolofSoftware,TsinghuaUniversity,Beijing100084)2(SchoolofInformation,CapitalUniversityofEconomicsandBusiness,Beijing100070)

Process mining is an emerging discipline providing comprehensive sets of tools to provide fact-based insights and to support process improvements. This new discipline builds on process model-driven approaches and data-centric analysis techniques such as machine learning and data mining. Conformance checking approaches, i.e., techniques to compare and relate event logs and process models, are one of the three core process mining techniques. It is shown that conformance can be quantified and that deviations can be diagnosed. BPMN 2.0 model has so powerful expression ability that it can express complex patterns like multi-instance, sub-process, OR gateway and boundary event. However, there is no existing conformance checking algorithm supporting such complex patterns. To solve this problem, this paper proposes an algorithm (Acorn) for conformance checking for BPMN 2.0 model, which supports aforesaid complex patterns. The algorithm uses A*algorithm to find the minimum cost alignment, which is used to calculate fitness between BPMN 2.0 model and the log. In addition, virtual cost and expected cost are introduced for optimization. Experimental evaluations show that Acorn can find the best alignment by exploiting the meanings of BPMN 2.0 elements correctly and efficiently, and the introduction of virtual cost and expectation cost indeed reduces the search space.

BPMN 2.0 model; complex pattern; A*search; conformance checking; alignment

2016-10-24；

2017-03-07

国家重点研发计划项目(2016YFB1001101)；国家自然科学基金项目(61472207，61325008，61402301) This work was supported by the National Key Research and Development Plan of China (2016YFB1001101) and the National Natural Science Foundation of China (61472207, 61325008, 61402301).

闻立杰(wenlj@tsinghua.edu.cn)

TP315