基于惯性补偿和MEMS的纯电动汽车坡道识别研究∗

罗 石，郑 超，朱长顺

基于惯性补偿和MEMS的纯电动汽车坡道识别研究∗

罗 石1，郑 超1，朱长顺2

(1.江苏大学汽车与交通工程学院，镇江 212013；2.江苏大学机械工程学院，镇江 212013)

本文中引入了基于惯性补偿和MEMS系统的坡道识别原理。采用惯性补偿法分解出MEMS三轴加速度计中的重力加速度分量，并利用它来修正MEMS陀螺仪模块的三轴角速度。通过四元数来表示车载坐标系与惯性坐标系的旋转关系，再将其转换为欧拉角，即可解算出电动汽车当前的坡道角。实车试验结果表明，这种算法精度高，实时性好，易于MCU实现。

电动汽车；坡道识别；惯性补偿；卡尔曼滤波；MEMS陀螺仪；MEMS加速度计

前言

结合坡道角能精确控制电机输出转矩，有效解决电动汽车坡道起步驱动力矩不足、坡道溜车等问题[1]；能设计符合坡道行驶规律的电动汽车AMT换挡策略，避免坡道频繁换挡；能设计出高效率的能量回收系统。由此可见，处理好坡道工况对电动汽车的安全性、经济性和舒适性有非常重要的意义。关于坡道识别的研究，有根据汽车纵向动力学设计出的坡道识别方法[2]，有利用传感器实测的纵向加速度与车速差分获得的加速度之间的差异设计出的基于加速度区间判断的坡道识别方法[3]，也有将汽车动力学原理与通过CAN总线获得发动机的转矩与转速相结合而设计出的坡道识别算法[4]。本文中则采用惯性补偿法获得重力加速度在车载坐标系三轴的分量，利用重力加速度向量的方向不变性，通过四元数姿态解算算法实时修正电动汽车的坡道角，可准确识别出电动汽车所处的坡道。本文中坡道角识别周期为20ms，采用的MCU是飞思卡尔的SPC5644。试验证明，本文中设计的坡道识别模块具有很强的实用性。

1 坡道识别原理简介

1.1 坡道识别的原理

惯性坐标系称为R系，车载坐标系(图中与一正方体固结者)为b系，如图1所示。这两个坐标系的关系可以用四元数旋转矩阵表示[5－6]:

图1 惯性坐标系与车载坐标系

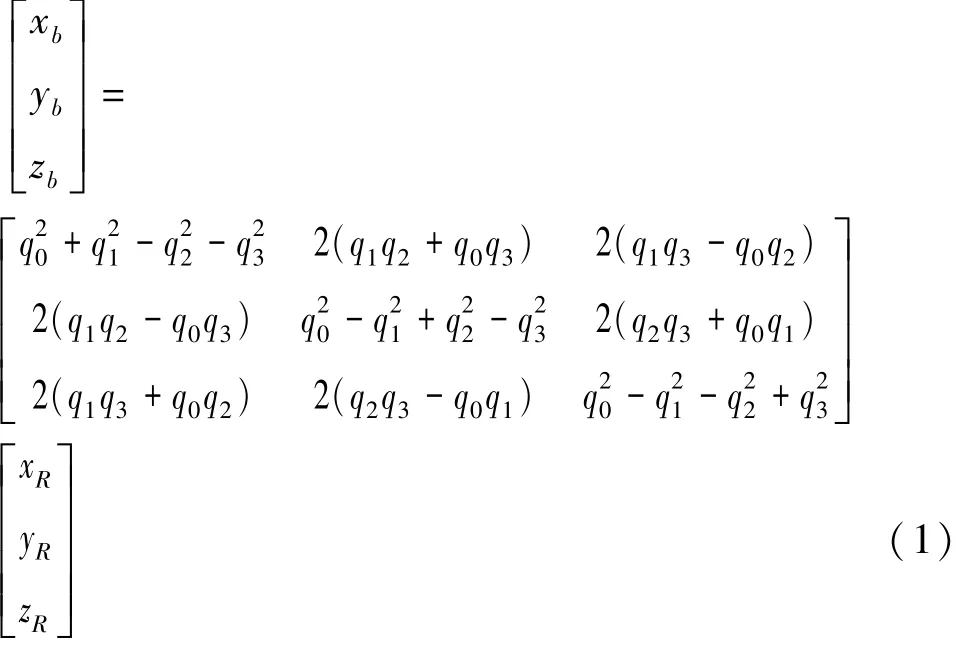
式中:q0，q1，q2和q3为四元数的4个参数；

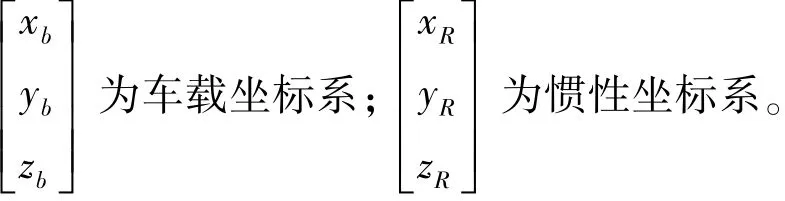
计算式(1)中的旋转矩阵即可确定R系与b系的旋转关系，理论上只要对MEMS三轴陀螺仪的角速度采用1阶Rung-kuta法，见式(2)，积分即可求出四元数q(t)，进而求得四元数旋转矩阵。

解为X(t＋Δt)＝X(t)＋Δt·f(X(t)，ω(t))

式中:θ为坡道角；γ为侧倾角；ψ为航向角。

1.2 坡道识别存在的问题

MEMS三轴陀螺仪存在零漂、噪声干扰等误差，这些误差会随着积分累积。根据1.1节设计坡道识别模块，并将坡道识别模块水平静止放置，实际测试40s，结果如图2所示(图2详细分析见4.1节)，坡道识别误差达到3.3°，所以必须对积分误差进行修正。本文中采用MEMS三轴加速度计测量的重力加速度修正MEMS三轴陀螺仪的积分误差。

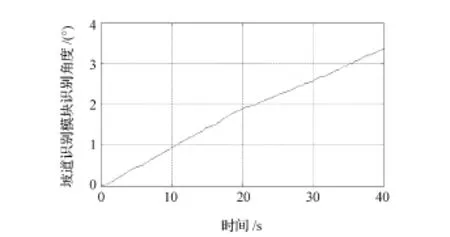
图2 MEMS陀螺仪积分误差

2 重力加速度修正与惯性补偿

由1.2节可知，由于积分误差的存在，坡道识别模块存在很大的零漂，采用重力加速度实时修正MEMS陀螺仪角速度即可消除累积误差。

重力加速度的方向始终垂直于地面，不会随着车载坐标系b系的变化而变化，这是重力加速度能修正MEMS三轴陀螺仪的理论基础，重力加速度在车载坐标系b系的分量可由MEMS三轴加速度计测量。

2.1 重力加速度修正原理

将惯性坐标系R系通过四元数Qt－1的旋转矩阵变换到bt－1系，此时R系中的重力加速度向量在bt－1系中的表达式为，在bt系中重力加速度向量经MEMS三轴加速度计测量、归一化后的表达是之间的误差代表着bt－1系与bt系之间的误差即，对这个误差进行PI调节，调节之后用来修正MEMS三轴陀螺仪的三轴角速度式中为原始数据滤波之后的向量；为 PI调节的输出。

此时，由Qt－1通过重力加速度修正过的经式(2)积分得到Qt:

设计PI调节器，根据bt－1系与bt系之间的误差进行PI调节，PI调节的输出为。根据式(4)修正MEMS三轴陀螺仪的三轴加速度。

将模块水平静止放置，且采用MEMS三轴加速度计测量的重力加速度修正MEMS三轴陀螺仪的角速度。如图3所示(图3详细分析见4.1节)，经重力加速度修正过的俯仰角误差稳定在0.1°，由此可见，采用重力加速度修正能消除积分误差。

图3 重力加速度修正积分误差

2.2 MEMS三轴加速度计测量重力加速度存在的问题

由2.1节可知，坡道识别模块在静止时，能够准确识别出坡道角。但是，电动汽车加速行驶时，则会产生较大的纵向加速度，此时MEMS三轴加速度计会受其干扰，测出的三轴加速度已不再是重力分量，如果将MEMS三轴加速度计的测量作为重力加速度来修正积分误差，坡道识别模块识别出的坡道角会有很大误差，如图4所示。针对这一问题，提出了惯性补偿法。

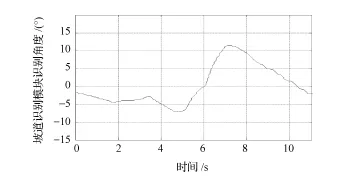
图4 无惯性补偿加速行驶

3 重力加速度的惯性补偿与信号处理

由2.2节可知，能否从汽车各种加速度中解耦出重力加速度是坡道识别准确与否的关键。MEMS的Z轴加速度去除路面随机振动干扰可得到较为准确的重力加速度在Z轴上的分量，通过这个Z轴分量可对X轴的解耦误差(解耦误差详见3.2节分析)进行限幅。

3.1 解耦重力加速度在Z轴上的分量

分析车载坐标系b系Z轴上的加速度，MEMS Z＝Gz＋bz(MEMS Z为MEMS三轴加速度计Z轴的测量结果，Gz为重力加速度在Z轴上的分量，bz为电动汽车垂直振动加速度，其中有用的是Gz，需要消除的是bz)，影响因素是bz，由于垂直振动加速度是路面随机振动，对于随机振动可采用平均值滤波法消除振动加速度干扰。

电动汽车在平直路面行驶工况下，采集车载坐标系b系Z轴的加速度16s。图5显示了滤波前后的Z轴加速度曲线。

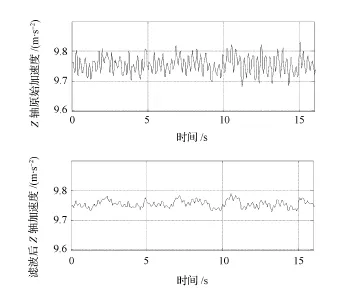
图5 滤波前后的Z轴加速度原始加速度

由图5可知，采用平均值滤波能有效消除路面随机振动对Z轴加速度的影响，从而获得较为准确的重力加速度在Z轴上的分量。

3.2 解耦重力加速度在X轴上的分量

影响电动汽车纵向加速度测量结果的因素非常复杂。分析车载坐标系b系X轴的加速度，MEMS X＝Gx＋ax＋bx(MEMS X为MEMS三轴加速度计X轴的测量结果，Gx为重力加速度在X轴上的分量，ax为电动汽车纵向加速度，bx为电动汽车纵向振动加速度，其中有用的是Gx，需要消除的是ax和bx(bx消除法见3.4节))，主要影响因素是ax，本试验采用获取车速脉冲并计算电动汽车纵向加速度法消除ax，但是，由于轮胎变形等因素影响，ax与电动汽车实际加速度不完全吻合，尤其是起步和制动阶段。针对起步和制动阶段提出了限制解耦误差修正MEMS X加速度法(Ex＝MEMS X－Gx－ax－bx，其中Ex为解耦误差)。3.2.1 计算电动汽车纵向加速度ax

本试验车在从动轴安装光电编码器，实时采集编码脉冲，实时计算电动汽车的纵向加速度，并滤掉bx得到ax。利用Gx＝MEMS X－ax，得到重力加速

式中:N1为t1时刻读取的脉冲个数；N2为t2时刻读取的脉冲个数；samper＿t为脉冲采样周期，ms；r为车轮半径，m；encoder为电机解码器的齿数；i为电动汽车主减速比。

3.2.2 限制解耦误差修正MEMS X加速度

电动汽车加速行驶时，由于轮胎存在滑移现象，计算的纵向加速度往往比实际加速度大，而且加速度越大，该误差就越大。电动汽车制动时，情况恰恰相反，这个误差与轮胎的滑移率有关，而滑移率无法测量。为此，本文中采用限定X轴测量值的方法，解决电动汽车加速度较大时的误差问题。

由于Z轴加速度经均值滤波后较为准确，这是限定X轴测量值的前提条件之一。由第2节可知，坡道识别模块静止误差在0.1°之内，这是前提条件之二。

绘制30°－0°角(识别范围为－30°～30°)，静态时，MEMS X轴加速度随MEMS Z轴加速度变化的关系图，如图6所示(－30°－0°的关系图与30°－0°的关系图呈镜像关系)，通过控制解耦误差Ex(Ex为上限与下限的比值减去理论值)限制X轴的加速度输出值。度在X轴的分量:

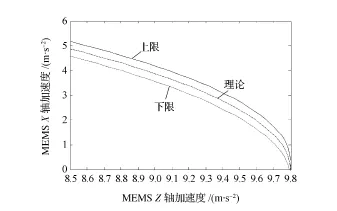
图6 MEMS X加速度限定关系

3.3 解耦重力加速度在Y轴上的分量

分析车载坐标系b系Y轴的加速度，MEMS Y＝Gy＋ay＋by(MEMS Y为MEMS三轴加速度计Y轴的测量结果，Gy为重力加速度在Y轴上的分量，ay为电动汽车向心加速度，by为电动汽车侧向振动加速度，其中有用的是Gy，需要消除的是ay和by(消除法见3.4节))，主要影响因素是ay，采用向心加速度代替侧向加速度，精度上可以满足使用要求，但是，由式(7)计算的向心加速度受电动汽车速度影响大，误差大，波动大。通过滤波消除by，利用Gy＝MEMS Y－ay得到重力加速度在Y轴上的分量。

式中:v为电动汽车纵向速度，m/s；ωz为电动汽车横摆角速度，rad/s。

由式(7)可知，想要获得准确的向心加速度，必须保证汽车的瞬时速度v和MEMS陀螺仪的Z横摆角速度ωz准确，但是v并不能准确计算出来，MEMS Y轴加速度与ay的差分可以认为是重力加速度在Y轴的分量，而这个分量理论上只是由于汽车侧倾引起的，所以根据汽车的最大侧倾角对Gy进行限幅处理。

3.4 MEMS加速度计和陀螺仪数据处理

由于MEMS三轴加速度计和三轴陀螺仪模块输出的车载坐标系b系的三轴加速度和三轴角速度存在噪声和振动加速度等干扰，须从干扰的信号中提取有用信号，获取真实值。为此设计了卡尔曼滤波器，对X轴滤波，消除bx和噪声干扰；对Y轴滤波，以消除by和噪声干扰。

卡尔曼滤波算法为

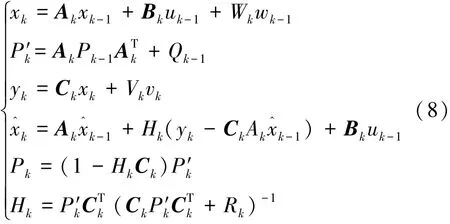
式中:Pk为协方差；Hk为卡尔曼增益。

图7和图8分别对比了卡尔曼滤波前后MEMS三轴加速度计的X轴加速度和陀螺仪的绕X轴角速度。此处仅以X轴为例，Y轴同理。

图7 卡尔曼滤波前后的MEMS X轴加速度

图8 卡尔曼滤波前后的MEMS陀螺仪绕X轴角速度

4 试验数据分析与验证

4.1 重力加速度修正积分误差验证

坡道识别模块水平静止放置40s，图2显示了无重力加速度修正时，坡道识别模块识别角度存在3.3°的漂移，角度漂移是MEMS陀螺仪积分误差造成的。图3显示了经过重力加速度修正过的俯仰角误差稳定在0.1°。由此可见，本文中提出重力加速度修正MEMS陀螺仪的积分误差法能够有效消除MEMS陀螺仪的积分误差。

无惯性补偿时，直接将MEMS三轴加速度计测量值作为重力加速度修正MEMS三轴陀螺仪积分误差，且电动汽车加速行驶时，坡道识别模块的识别结果如图4所示，坡道识别模块识别结果存在严重误差。

4.2 坡道识别的坡道实车试验

检验电动汽车在水平道路匀速行驶、加速行驶工况下识别的坡道角是否正确。图9显示了在水平路面匀速行驶工况下，坡道识别模块能准确识别出当前的坡道值。图10显示了电动汽车加速行驶工况下，且无惯性补偿时，坡道识别模块不能准确识别坡道。图11显示了经过惯性补偿之后，坡道识别模块能准确识别当前所处的坡道值，误差在1°之内。

检验电动汽车在10°坡道角匀速行驶、加速行驶工况下是否能正确识别坡道。图12显示了电动汽车在10°坡道匀速行驶时，坡道识别模块识别的当前坡道角是10°，与实际坡道吻合。图13显示了电动汽车由水平路面加速上坡时，且未对重力加速度惯性补偿时，坡道识别模块识别的角度误差很大。图14显示了经过惯性补偿后的坡道识别模块能够准确识别当前坡道角。

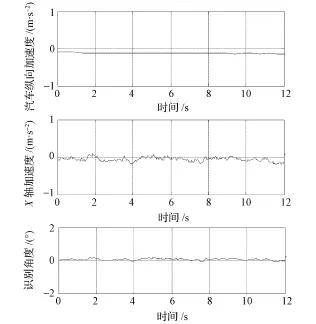
图9 电动汽车匀速行驶

图10 电动汽车加速行驶

图11 惯性补偿后加速行驶

图12 坡道匀速行驶

图13 坡道加速行驶

5 结论

本文中提出了基于惯性补偿和MEMS的电动汽车坡道识别方法，通过大量试验验证，此方法实时识别出的坡道误差小，实用性强，计算速度快，20ms更新一次坡道角，并能通过CAN总线实时发送坡道角。结合坡道信息设计电动汽车AMT、坡道起步控制和能量回收策略，能提高电动汽车安全性、经济性，基于坡道识别的电动汽车控制系统是电动汽车未来发展的方向。

图14 惯性补偿的坡道加速行驶

[1] 陈淑江，秦大同，胡明辉，等.纯电动汽车坡道自适应起步控制策略[J].重庆大学学报，2012，35(9):1-7.

[2] 金辉，葛安林，秦贵和，等.基于纵向动力学的坡道识别方法研究[J].机械工程学报，2002，38(1):79-82.

[3] 金辉，李磊，李斌虎，等.基于加速度区间判断的坡道识别方法[J].中国公路学报，2010(1):122-126.

[4] 王玉海，董瑞先，王松，等.基于SAE J1939协议的重型车辆坡道识别实时算法[C].2010中国汽车工程学会年会论文集，2010.

[5] 张荣辉，贾宏光，陈涛，等.基于四元数法的捷联式惯性导航系统的姿态解算[J].光学精密工程，2008，16(10):1963-1970.

[6] 段栋栋.高精度MEMS陀螺仪的滤波算法研究[D].成都:电子科技大学，2014.

[7] KHOSHNOUD F，DE SILVA C W.Recent advances in MEMS sensor technology-biomedical applications[J].IEEE Instrumentation＆Measurement Magazine，2012，15(2):14-24.

[8] 梁延德，程敏，何福本，等.基于互补滤波器的四旋翼飞行器姿态解算[J].传感器与微系统，2011，30(11):56-58.

[9] 梁丽娟.基于机器人及军用导航系统的MEMS陀螺仪性能研究[D].北京:北京交通大学，2011.

[10] 苑艳华，李四海，南江.基于卡尔曼滤波器的航姿系统测姿算法研究[J].传感技术学报，2011，24(12):1718-1722.

[11] XIAO D，GHOSH B K，XI N，et al.Sensor-based hybrid position/force control of a robot manipulator in an uncalibrated environment[J].IEEE Transactions on Control Systems Technology，2000，8(4):635-645.

[12] LI M，XIANG C，JIA P，et al.A study on a dynamic algorithm for vehicle attitude by using rotary encoder[J].Automotive Engineering，2014，36(7):857-861.

[13] LU X，WANG P，GAO B，et al.Model predictive control of AMT clutch during start-up process[C].Chinese Control and Decision Conference(CCDC)，2011:3204-3209.

[14] GU Q，CHENG X.Study on optimal slip ratio identification and traction control for electric vehicle[C].Mechatronic Science，E-lectric Engineering and Computer(MEC)，2011 International Conference on.

A Research on Slope Recognition with Pure Electric Vehicles Based on Inertia Compensation and MEMS

Luo Shi1，Zheng Chao2＆Zhu Changshun2
1.Automotive and Traffic Engineering of Jiangsu University，Zhenjiang 212013；2.Mechanical Engineering of Jiangsu University，Zhenjiang 212013

A slop recognition principle based on inertia compensation and MEMS is introduced in this paper.Specifically，inertia compensation method is adopted to decompose the gravity component in MEMS three-axis accelerometer，which is then used to correct three-axis angular velocity in MEMS gyroscope module.The rotation relationship between vehicle coordinate system and inertial coordinate system is expressed by quaternion，which is then transformed into Euler angles to calculate the angle of slope electric vehicle is currently running on.The results of real vehicular tests show that the scheme used has high accuracy，good real-time performance，and is easy to implement in MCU.

electric vehicle；slope recognition；inertia compensation；Kalman filtering；MEMS gyroscope；MEMS accelerometer

10.19562/j.chinasae.qcgc.2017.08.012

∗江苏省高校重大基础研究项目(13KJA58001)资助。

原稿收到日期为2016年8月21日。

郑超，硕士研究生，E-mail:874722877＠qq.com。