利用放电电压平台的FCM电池分选方法∗

张 睿，周永勤，李 然

利用放电电压平台的FCM电池分选方法∗

张 睿，周永勤，李 然

(哈尔滨理工大学电气与电子工程学院，哈尔滨 150080)

针对电池分选成组后的一致性问题，在分析电池容量衰减与放电电压曲线关系的基础上，采用模糊C均值聚类算法，提出一种基于放电电压平台的FCM电池分选方法。该方法选取单体电池放电电压平台的3个特征点作为样本，再将标准化后的样本集作为算法的分类对象，最后以聚类有效性函数判定最优分类结果。全寿命实验的结果表明，采用分选方法得到的电池组动态一致性好，循环寿命衰减率降低，在500次循环寿命测试后健康度仍保持在90%以上。所提出的分选方法分选效率高，适用于数量较大的电池样本，可有效识别组内电池样本的一致性和生产质量，实现电池的多场合利用和效率最大化。

磷酸铁锂电池；模糊C均值聚类；放电电压平台；一致性；健康度

前言

由于单体电池在生产过程中的差异，在成组使用时循环寿命比单体使用时衰减更快，这是由单体电池间的不一致性造成的。电池活化程度不一致、电解液注液浓度不一致等都会引起电池间的不一致。电池在生产过程中造成的不一致，会随着电池在使用中循环充放电次数的增加而强化，导致单体电池的容量等性能差异在使用过程中逐步扩大。容量较低的单体电池变成了负载，由容量较高的单体电池对其充电，引起这些单体电池的过充或过放，导致电池组寿命快速衰减，最终失效[1－3]。因此，单体电池的不一致会严重影响电池组的容量、寿命和安全。由于目前的生产技术不能完全消除电池间不一致，因此在未来相当长的一段时间，单体电池间的绝对差异是始终存在的。因此，对电池一致性和成组方法的研究有重要意义。

目前，国内对电动汽车电池的研究主要集中在电池的等效模型和均衡策略等方面[4－7]，而对动力电池的一致性和分选方法的研究较少[8－12]。现有研究可大致归为两类，一类是以不同电池某一参数对应特征点之间的欧氏距离为指标，应用不同的统计方法达到分选目的[9－10]；另一类是对电池提取多种参数，通过参数指标对电池性能进行综合判定，或通过统计方法剔除相关性弱的参数指标，利用其余参数筛选一致性较好的电池[11－12]。这两种方法均能根据电池的实际差异，得到较明确的分选结果，但算法复杂，有一定的实施难度。事实上，电动汽车要普及使用，动力电池的循环寿命至关重要[13]。电池的成组一致性直接影响电池的容量衰减和循环寿命，若采用电池的循环寿命作为电池成组一致性的评价指标，将更具工程实际意义。考虑到电池容量衰减与放电电压曲线密切相关，放电电压曲线在稳定阶段中存在一个较宽的平台期，这个平台期稳定时间越长，说明制造工艺越好，容量衰减越慢。因此，本文中着眼于电池的放电曲线，结合模糊C均值聚类算法，提出一种基于放电电压平台的电池分选方法。该方法选取单体电池放电电压平台上的特征点，以特征点标准化后的数据集作为该算法的分类对象，以聚类有效性指标确定最佳分类数和分类结果，选取电池健康度作为分类结果评价指标。该方法适用于大数量电池样本，分选效率高。

1 FCM算法研究

1.1 FCM算法

模糊C均值聚类算法(fuzzy C-means algorithm，FCM)是一种较成熟的模糊聚类算法。FCM算法的思想如下:

假定单体电池样本集X＝{x1，x2，…，xn}分为c类，设U是一个c×n的矩阵，其元素μij表示第j个电池样本属于第i类的隶属度，因一个数据集的隶属度之和总等于1，故必须满足约束条件，即

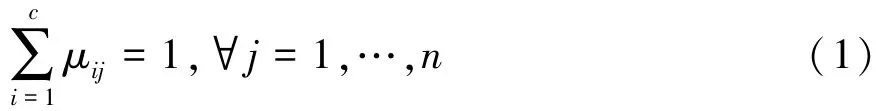
FCM算法的目标函数定义为

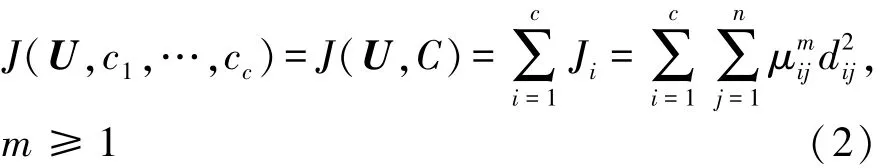
ci表示第i类电池的聚类中心，dij＝‖xj－ci‖表示第i类聚类中心到第j个电池样本的欧氏距离。m是一个加权指数，它决定了类别之间的相关程度，m值越大，聚类结果的模糊性也越大。在无特殊要求的情况下，可取m＝2[14]。

FCM算法通过迭代运算使目标函数达到极小值。为求在约束条件下目标函数的极小值，由拉格朗日乘子法构造新函数，即

式中:λ为拉格朗日乘子，d2ij＝‖xj－ci‖2。分别求F对参数λ，μij的偏导数和J(U，C)对ci的偏导数，可以得到式(2)取最小值的必要条件:

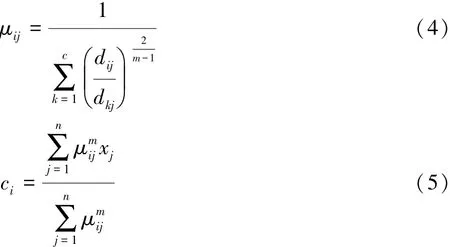
FCM算法步骤是:(1)设定分类数c，设定迭代停止条件ε，初始化隶属度矩阵U；(2)由式(5)计算c个聚类中心；(3)由式(2)计算目标函数，当目标函数值相对于上次目标函数值的改变量小于ε时迭代终止，否则由式(4)计算新的隶属度矩阵并返回到步骤(2)。

1.2 FCM算法有效性指标

FCM算法需要预先确定分类数c，在实际应用中最佳分类数c一般是未知的。对应不同的c值时，算法得到的模糊聚类划分也不同。聚类有效性指标可以帮助确定最优的划分，从而得到最佳的分类数。

本文中选用文献[15]中提出的有效性函数，构建了求和型聚类有效性指标VFS:

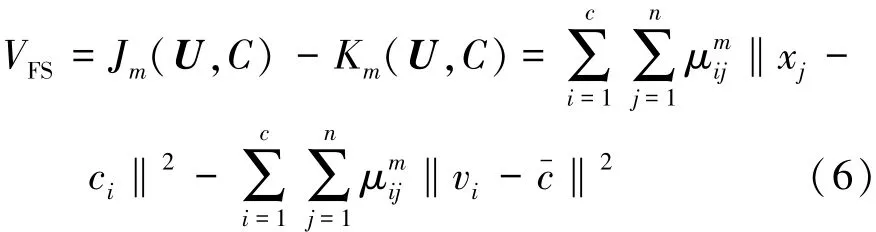
式中ci为第i类聚类中心，

VFS为一个极小型指标，即极小值对应的聚类数为最佳聚类数。

1.3 FCM算法的有效性分析

式(4)中μij表示第j个电池样本隶属于第i类的程度，将该式变形为

由式(7)不难发现，μij越大，则dij越小，dkj越大。即第j个电池样本xj到第i类聚类中心ci距离越近，而距离其他的聚类中心越远。所以，测量模糊隶属度是评价聚类优劣的重要因素[16]。

由式(6)可知，本文中选用的有效性指标VFS由两项组成，第1项以样本到聚类中心的欧氏距离描述数据的紧致性，第2项以各类聚类中心到数据中心的欧氏距离描述类间的分离性，模糊隶属度作为这两个欧氏距离的加权因子，两者之差即为有效性指标VFS的值。在VFS中第1项值越小说明同类数据越相似；第2项值越大代表数据类间分离越明显。因此，VFS越小，聚类效果越好。综上所述，在VFS的指导下，分类结果是在兼顾数据的几何结构和模糊隶属度的前提下得到的[17]。因此，该方法可全面地评价电池分类质量，帮助选择合适的分类数目，实现电池的最优分选。

2 电池分选方法的实现

2.1 充放电循环实验

为获取电池样本放电曲线，对容量为1 100mA·h的磷酸铁锂电池样品进行充放电循环，如表1所示。

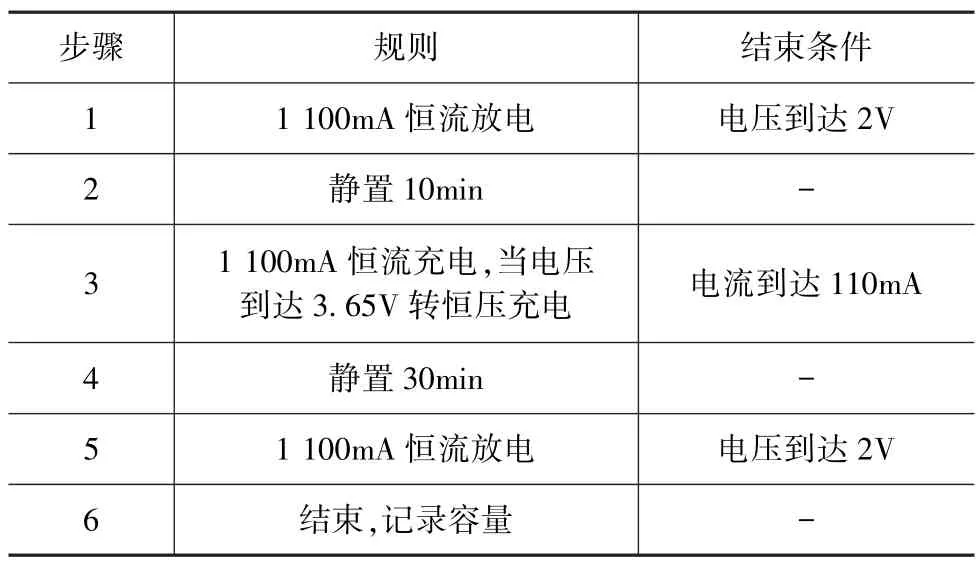
表1 电池充放电循环工艺

选取某电池厂家新出厂同一批次的100只容量为1 100mA·h的磷酸铁锂电池样品作为样本1～100，其中对样本1～90实施步骤1～步骤6。在步骤5得到的样本1的恒流放电曲线如图1所示。

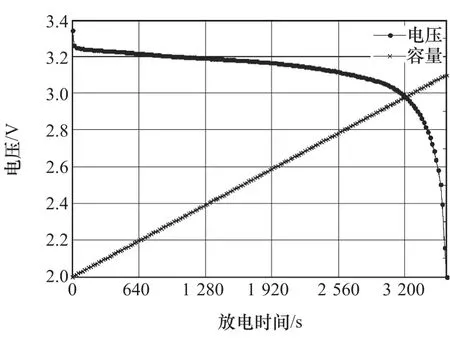
图1 样本1放电电压平台曲线

电池恒流放电时，电压会经历3个阶段。放电初期，电压下降稍快；随后放电曲线逐渐趋于平缓，这一阶段对应的电压值通常称为放电电压平台，其持续的时间与放电倍率、电池质量和寿命等因素相关；在放电末期，曲线会呈现急剧下降的趋势。因此，放电平台是磷酸铁锂电池的一个重要性能参数，也是体现各只电池的容量等性能差异的重要因素。

2.2 充放电循环实验

根据FCM聚类算法的基本原理，为保证聚类对象的维数相同，必须保证对每只电池选取的特征点个数相同。根据同型号不同电池放电平台趋势相近的特点，考虑到选取的特征点须全面反映电池不一致性，故在每只电池放电电压平台的相同时间位置上提取3个特征点，分别为电压放电平台初期稳定时刻t1电压、电压平台中间时刻t2电压和平台期结束时电压差异较大时刻t3电压。得到的样本1～90放电曲线和单体电池特征点如图2所示。

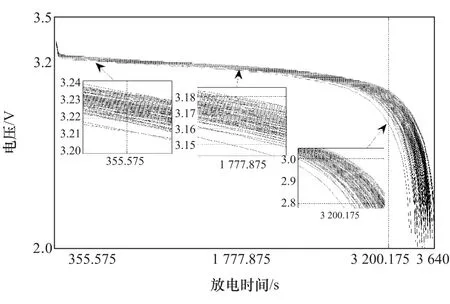
图2 样本1～90放电曲线和单体电池特征点

样本1～90的放电曲线中，取t1，t2，t3分别为90只电池样本平均放电时间的10%，50%，90%，特征点信息如表2表述。

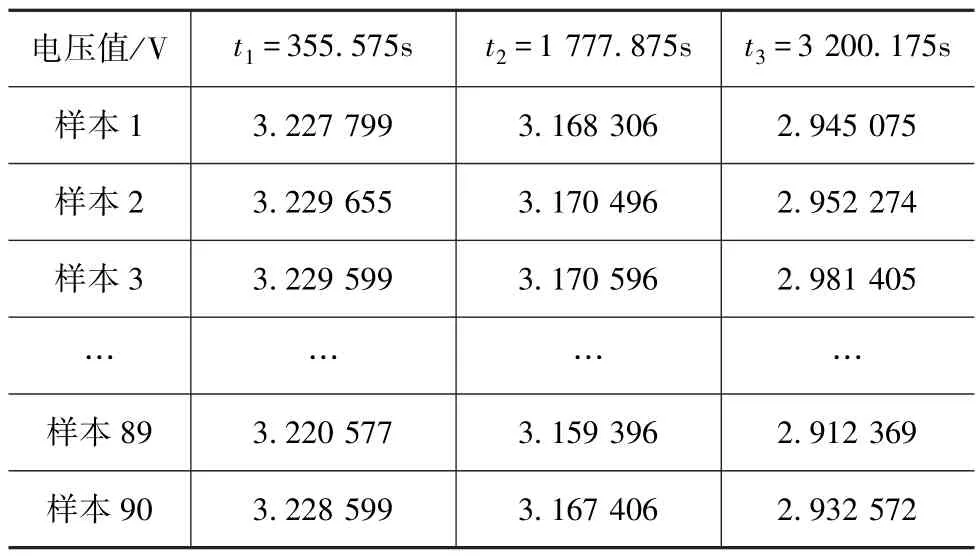
表2 电池特征点信息

将上述特征点变换为三维矩阵，即

式中:uij(1≤i≤90，1≤j≤3)代表第i只电池样本第j个特征点。

式(8)通过极差变换进行标准化处理，得到三维矩阵V′，即

2.3 FCM聚类算法结果

式(9)中V′即为FCM算法的聚类对象。通过MATLAB编程，分类数c分别取2～4，迭代停止条件ε取1×10－5，对V′应用FCM算法。得到分类结果分别如表3～表5所示。

表3 分类数c＝2的分类结果

表4 分类数c＝3的分类结果

表5 分类数c＝4的分类结果

分类数c分别为2～4时，计算得到的有效性函数值VFS如表6表示。

表6 有效性函数取值

分类数c为2～4时，样本1～90的分类效果如图3～图5所示。

分类数c取2～4时，有效性函数VFS在c＝3时取值最小，分类效果最好。由表4可见，c＝3时的第1类聚类中心在数值上大于第2类和第3类，说明第1类样本放电电压平台维持较长，电性能较好。因此这种分选方法既能保证分类结果明确，又能区别各分类结果中电池电性能的差异。在工程实际中，可按照不同类别将电池灵活应用在不同要求的技术场合。

随着分类数c的取值增大，可能会出现有效性函数VFS的值减小或增大的趋势，但分类数过多对电池分选成组的应用意义不大，本文中不予讨论。

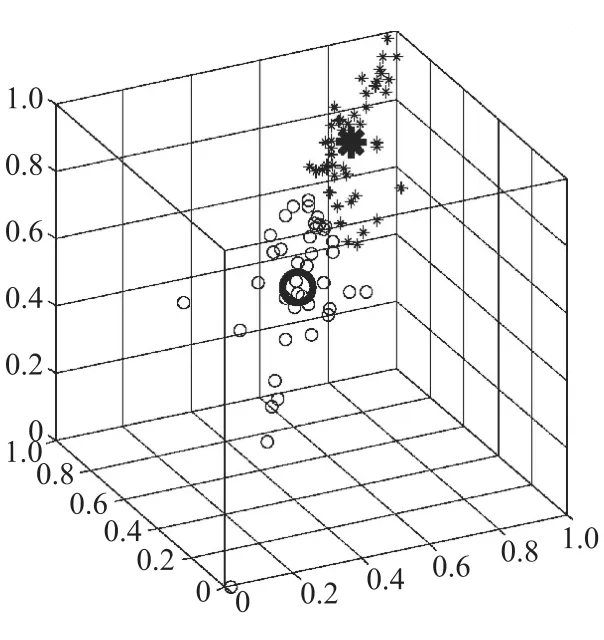
图3 分类数c＝2

图4 分类数c＝3

图5 分类数c＝4

2.4 分选方法的有效性分析

聚类方法是一种无监督的机器学习方法，在事先没有任何数据分布特点信息的前提下，要求同一类内的数据对象相似度尽可能大，不同类间的数据对象相似度尽可能小。对电池性能好坏等这类的划分没有严格的界限和标准，因此采用模糊聚类方法达到对电池分选的目的。本文中采用的FCM聚类算法，在传统硬划分方法加入模糊元素，能提高算法的灵活性和智能程度，也能通过数字特征客观地反映不同电池间的性能差异，实现电池分选成组的最优化。

对于分选方法的有效性，很难从现有文献找到一种聚类方法能得到所有数据集的最优划分[18]，通常是通过构建聚类有效性指标实现对模糊聚类方法的有效评价，因此对电池的分选也很难得到最优结果。随着电池检测技术的快速发展，对电池电压等参数的采集已经达到较高精度，在放电平台上采集的特征点能够具有较好的区分度，因此选取FCM聚类算法作为电池分选方法是可行的。本文中选取的有效性指标VFS同时考虑数据结构和模糊隶属度，是一种常用的有效性指标，能全面评价聚类划分质量，在它指导下的分类结果是可信的。

3 循环寿命测试

为验证上述分选方法的有效性，从表4 c＝3的分类结果中在第1类30只电池中随机抽取10只样本并联成电池组1，在第2类38只电池中随机抽取10只样本并联成电池组2，在第3类22只电池中随机抽取10只样本并联成电池组3。将未经过任何筛选处理的样本91～100共10只电池并联成电池组4。通过其他抽取方法组成电池组5～6。电池成组方式如表7所示。

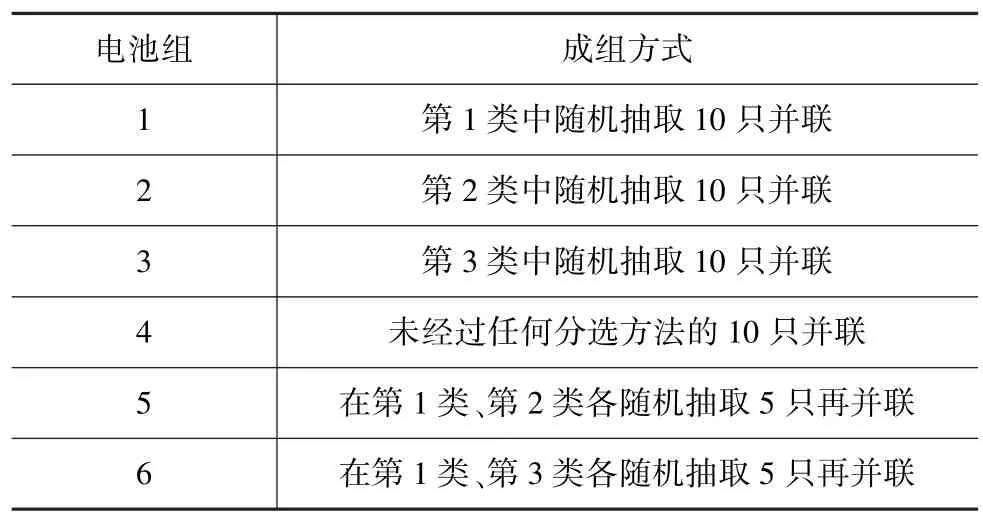
表7 电池成组方式

对6个电池组进行循环寿命测试，其流程见表8。

表8 循环寿命测试规范

选取电池健康度SOH作为实验评价指标。电池SOH用于描述电池的健康度状态，是目前电动汽车动力电池系统中最重要的性能指标之一。电池健康度的标准定义是指动力电池在标准条件下SOC从100%放电到截止电压所放出的电量除以它的标称容量，用%表示。

QC/T 743—2006《电动汽车用锂离子蓄电池》行业标准[19]中第6.2.11款规定:在(20±2)℃下的循环寿命实验中，当电池组容量下降到其额定容量的80%时判定锂离子电池失效。测试时，当电池组放电容量小于8 800mA·h，即SOH小于80%时结束实验，得到实验结束时各电池组的循环寿命，如表9所示。

表9 循环寿命测试结果

将电池组1～4的实验结果进行汇总分析，如图6所示。

图6 电池组1～4容量衰减曲线

4个电池组中，未应用任何分选方法并联组成的电池组4循环寿命最短，通过分选方法得到的电池组1～3循环寿命均高于电池组4。电池组1～3中，电池组1在超过500次循环时依然能保持90%的健康度，说明3个分类结果中，第1类具有最好的容量衰减动态一致性，健康度稳定性最高，此分类结果的电池样本可成组应用在军事领域等技术要求严格的场合；第2类、第3类则可分别应用在工业生产和民用领域。实验表明，由分选方法得到的3个分类结果循环寿命衰减率均得到有效控制，与不使用任何分选方法的电池组相比，一致性较好。

将电池组1～3、5和6的实验结果进行汇总分析，如图7所示。

由第1类与第2类电池并联而成的电池组5循环寿命较短，第1类与第3类电池并联而成的电池组6循环寿命最短，一致性最差。由实验结果可知，因不一致的单体电池会严重影响电池组的循环寿命，所以来自不同分类结果的电池并联而成的电池组循环寿命衰减更明显。由此说明了对动力电池进行分选的必要性，也间接证明了本文中研究方法的可行性和有效性。

图7 电池组1～3和5～6容量衰减曲线

该方法在分析放电电压平台与电池容量等性能之间关系的基础上，采用电压平台上的特征点作为分类依据以达到分选目的。虽然本文中的研究对象为磷酸铁锂电池，但对于其他不同类型的电池，例如铅酸电池、镍氢电池等，由于它们在放电过程同样存在较为稳定的电压平台，故同样适用。

4 结论

针对电动汽车电池成组使用时的不一致问题，在研究电池容量衰减与放电电压曲线关系的基础上，结合FCM算法，提出了一种基于放电电压平台的电池分选方法。该方法只需提取放电曲线上的特征点即可完成分选，思路清晰、实施容易，对大数量的电池样本分选效率高。实验结果表明，采用该分选方法得到的电池组循环寿命衰减率降低，动态一致性好，最优分类结果在500次循环寿命测试后健康度仍能保持在90%以上。因此，根据分选结果可按照不同技术要求灵活应用在工业领域、民用设备等多种场合，实现电池利用效率的最大化。

[1] 戎袁杰，李春文，李建敏，等.基于燃料电池的电能质量控制器设计[J].电机与控制学报，2009，13(S1):52－55.

[2] ANTONIO A，ALBERTO B，GIOVANNI F，et al.Battery choice and management for new-generation electric vehicles[J].IEEE Transactions on Industrial Electronics，2005，52(5):1343－1349.

[3] LEE Y S，CHENG G T.Quasi-resonant zero current switching bidirectional converter for battery equalization applications[J].IEEE Transactions on Power Electronics，2006，21(5):1213－1224.

[4] 陈坤华，孙玉坤，李天博，等.电动汽车锂离子电池建模和剩余容量估计[J].汽车工程，2014，36(4):404－408.

[5] 罗玉涛，王峰，喻皓，等.基于行驶工况的磷酸铁锂电池寿命模型研究[J].汽车工程，2015，37(8):881－885.

[6] 王亚军，王旭东，周永勤，等.准抗毁化电源蓄电池SOC预测的GA-BP网络方法[J].电机与控制学报，2010，14(6):61－65.

[7] 王磊，朱建新.深度混合动力汽车电池组动态诊断与均衡策略研究[J].汽车工程，2013，35(8):687－690.

[8] 戴海峰，王楠，魏学哲，等.车用动力锂离子电池单体不一致性问题研究综述[J].汽车工程，2014，36(2):181－188.

[9] 王佳元，孙泽昌，魏学哲，等.电动汽车动力电池分选方法研究[J].电源技术，2012(1):94－98.

[10] 王东梅，冯伟峰，白红燕，等.基于电压平台的电池聚类分选算法研究[J].电源技术，2016(5):994－996.

[11] 王震坡，孙逢春，张承宁.电动汽车动力蓄电池组不一致性统计分析[J].电源技术，2003(5):438－441.

[12] 多智华，李革臣，张宏，等.自动曲线识别的电池分类系统[J].电源技术，2000(2):99－102.

[13] 徐顺刚，王金平，许建平.一种延长电动汽车蓄电池寿命的均衡充电控制策略[J].中国电机工程学报，2012(3):43－48.

[14] 于剑.论模糊C均值算法的模糊指标[J].计算机学报，2003 (8):968－973.

[15] FUKUYAMA Y，SUGENO M.A new method of choosing the number of clusters for the fuzzy c-means method[C].Kobe:Proceedings of 5th Fuzzy Systems Symposium，1989.

[16] 李爱生，柳健，黄铁侠.模糊聚类的有效性分析[J].无线电工程，1991(3):18－25.

[17] 周开乐，杨善林，丁帅，等.聚类有效性研究综述[J].系统工程理论与实践，2014(9):2417－2431.

[18] PAL N R，BISWAS J.Cluster validation using graph theoretic concepts[J].Pattern Recognition，1997，30(6):847－857.

[19] 全国汽车标准化技术委员会.QC/T 743—2006电动汽车用锂离子蓄电池[S].2006.

A Battery Sorting Scheme Based on Fuzzy C-mean Clustering，Taking Advantage of the Flatness of Discharge Voltage Curve

Zhang Rui，Zhou Yongqin＆Li Ran
School of Electrical and Electronic Engineering，Harbin University of Science and Technology，Harbin 150080

To solve the consistency problem of batteries after being sorted into groups，on the basis of analyzing the relation between battery capacity losses and discharge voltage and adopting fuzzy C-mean clustering algorithm，a battery sorting scheme is proposed，taking advantage of the flatness of discharge voltage curve.With the scheme，three characteristic points on the flat segment of discharge voltage curve for each cell are chosen as samples and with normalized sample set as the sorting object of the algorithm，the optimal sorting results are finally judged by clustering validity function.The results of whole-life experiment show that the battery pack sorted by the scheme proposed has good dynamic consistency and lower cycle life decay rate，with its SOH remains above 90%after 500 cycles of life tests.The battery sorting scheme proposed has high sorting efficiency and is suitable for large quantities of battery samples，and can effectively identify the consistency and production qualities of battery samples in a pack，achieving various occasion utilization and efficiency maximization of batteries.

lithium iron phosphate battery；fuzzy C-means clustering；flat segment of discharge voltage curve；consistency；state of health

10.19562/j.chinasae.qcgc.2017.08.003

∗国家重点研发计划(2016YFC0300100)资助。

原稿收到日期为2017年2月21日，修改稿收到日期为2017年5月15日。

周永勤，教授，E-mail:zhouyongqin＠hrbust.edu.cn。