无储能单元串联式电传动车辆直流母线电压鲁棒控制的研究∗
2017-09-15SaeidHabibi
宋 强,李 松,Saeid Habibi
无储能单元串联式电传动车辆直流母线电压鲁棒控制的研究∗
宋 强1,2,李 松1,2,Saeid Habibi3
(1.北京理工大学机械与车辆学院,北京 100081; 2.北京理工大学协同创新中心,北京 100081;3.麦克马斯特大学,汉密尔顿,加拿大 L8S4L8)
鉴于一般串联式电传动车辆带有一定容量的储能单元,导致系统体积大、成本高、寿命低等缺陷,提出一种无储能单元的串联式电传动系统,并针对取消储能单元带来的母线电压波动问题,在传统电压和电流双闭环PI控制基础上加入模糊控制,制定了模糊自适应PI控制的直流母线电压控制策略,提出了PI参数的在线自整定方法。搭建无储能单元串联式电传动系统的Matlab/Simulink模型,对模型和控制策略进行仿真。结果表明,模糊自适应PI控制策略有利于提高系统的响应速度,减小电压的超调量,增强系统鲁棒性,有更好的静、动态性能。
串联式电传动系统;储能单元;直流母线电压;模糊自适应PI控制;鲁棒性
前言
一般情况下,串联式电传动车辆直流母线处并联有电池或超级电容等储能单元,当发电机发电功率不能恰好满足驱动电机需求功率时,储能单元存储或放出电能,确保驱动电机的功率需求;储能单元可将直流母线电压维持在一定的工作范围内,避免母线电压过大地下降或升高,防止整流器或逆变器产生电压保护、电子器件击穿等威胁系统安全的情况发生[1-6]。但由此带来的问题是,储能单元的使用会使电传动系统体积增大、成本升高,同时又降低系统的使用寿命[7]。为解决取消储能单元带来的母线电压波动问题,国内外学者做了许多研究。
文献[8]中在电压、电流双闭环基础上采用负载电流前馈的控制方法,但负载电流是随开关状态变化的一个不规则的脉动波,对其采样比较困难,而且须采用低通滤波器得到其平均值,降低了系统的动态响应速度。文献[9]中采用主从控制方案,以系统的整流器侧作为主控制系统,驱动电机侧作为从控制系统,使电流有较好的跟随性,从而保证母线电压的稳定。但这种控制方法使控制结构复杂,系统有较大的延迟。文献[10]中采用电流平衡控制方法,始终保持整流器流出的电流等于逆变器输入的电流,以抑制母线电压的瞬态波动。文献[11]中通过构建负载状态前馈通道,将驱动电机侧瞬时有功功率直接前馈到发电机,从而避开了相对缓慢的电压外环间接调整功率的过程,加快了系统的响应速度。
以上双变换器直流母线电压稳压方法均假定整流器输入的三相电来自电网,当系统稳定时,输入的三相电恒定。但串联式电传动车辆整流器输入的三相电来自发电机,当负载变化时,特别是在无储能单元条件下,发电机功率必然会随之产生剧烈变化,整流器输入的三相电并非恒定,因此,以上方法均不能解决无储能条件下串联式电传动车辆直流母线电压稳定性的难题。
本文中提出了一种基于模糊控制的PI参数自整定的直流母线电压控制方法,建立了无储能装置串联式电传动系统模型,在电压电流双闭环控制的基础上,提出了具有参数自整定功能的模糊PI控制器,通过模糊推理方法对PI参数进行在线自整定。在Matlab/Simulink环境下建立了仿真模型,动态负载仿真结果表明,该控制策略大大降低了系统的超调量,提高了系统的鲁棒性。
1 串联式电传动系统建模
典型的无储能装置串联式电传动系统结构如图1所示,一般情况下,无储能装置的串联式电传动系统包括发动机、发电机、整流器、逆变器和驱动电机。
发动机-发电机构成发电机组,其中,此处发动机为柴油机,采用转速控制模式;发电机和电动机均为永磁同步电机,均采用转速控制模式,相应的数学模型如下。

图1 无储能装置串联式电传动系统结构图
1.1 永磁同步发电机建模
在d-q轴旋转坐标系下,永磁同步发电机的电压和电磁转矩数学关系[12]为

式中:ugd,ugq分别为d,q轴电压分量;igd,igq分别为d,q轴电流分量;Lgd,Lgq分别为d,q轴电感分量;ψgd,ψgq分别为d,q轴磁链分量;Rgs为定子电阻;ψgf为永磁体基波励磁磁场对定子绕组磁链;ω1为电气角速度;p为微分算子。
发电机电磁转矩方程为
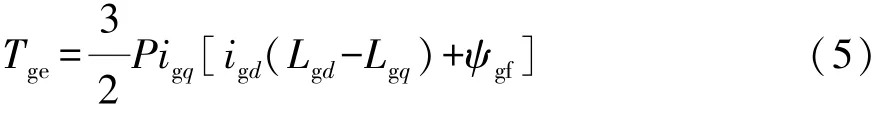
运动方程为

式中:Tm为发动机输出转矩;Tge为发电机电磁转矩;Jg为发电机转动惯量;P为发电机极对数;B1为阻尼系数。
发电机组的仿真模型如图2所示,其中图2(a)为发电机的Simpower模型,图2(b)为发动机的恒转速控制模块。
图中,采集的转子角速度ωm经过计算得到发动机-发电机组的轴转速n,通过转速控制模块计算获得相应转速下发电机的工作转矩,通过控制发电机的工作转矩获得不同的发电电力输出。
发电机的电压电流双闭环控制框图如图3所示。
1.2 整流器、逆变器建模
系统中的整流器为电压型PWM整流器,典型的三相PWM整流器的主电路拓扑如图4所示。
定义开关函数(Su,Sv,Sw)[13]:

图2 发电机组仿真模型

图3 电压电流双闭环控制框图
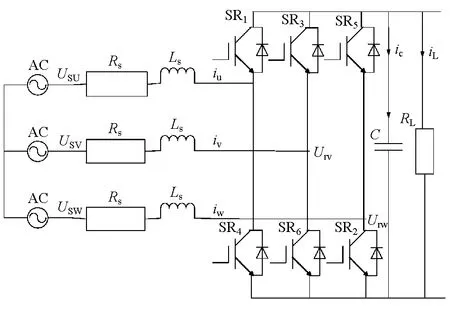
图4 三相PWM整流器的主电路拓扑


式中:off为关断;on为导通。
PWM整流器在d-q同步旋转坐标系下的表达式为

式中:ird,irq分别为d,q轴电流;udc为直流母线电压;C为电容值;Rs,Ls分别为每相电阻和电感;usd,usq分别为d,q轴电压;SRd,SRq分别为PWM变流器的d,q轴开关函数。
PWM整流交流电压满足以下关系:

逆变器模型与整流器类似。
1.3 永磁同步电动机建模
永磁同步电动机模型与永磁同步发电机模型基本相似,永磁同步电机在d-q坐标系下的磁链方程[14]为

电压方程为

由于电机控制最终要转化为d,q坐标下的控制,故还需要永磁同步电机d,q坐标系下的转矩方程:

而电动机运动方程为

式中:Tme为驱动电机电磁转矩;TL为负载转矩;Jm为驱动电机转动惯量;ω2为驱动电机电角速度;B2为阻尼力矩。
仿真模型如图5所示。

图5 驱动电机仿真模型
2 模糊PI控制器参数自整定
2.1 模糊PI控制器基本原理
传统PI控制器参数整定后一般不变,因此不能满足在线自整定的要求。本文中将模糊原理应用到PI参数的在线整定中,实时地调整PI参数[15],原理如图6所示。其中两个输入为误差e和误差变化率ec,两个输出为ΔKp和ΔKi。

图6 模糊自整定PI原理框图
通过检测母线电压,计算出实际母线电压与目标电压之间的误差e及其变化率ec,将这两个量输入到模糊控制器,经过模糊化、模糊推理和解模糊等过程得出Kp和Ki的调整量ΔKp和ΔKi[16],通过式(16)进而实现PI参数的在线自整定。

式中:Kp0,Ki0为已经整定的初始参数。
2.2 变量的模糊化与隶属度函数
将输入量误差e、误差变化率ec和输出量ΔKp与ΔKi都定义在模糊论域(-3,3)上,对应的7个模糊语言变量为负大(NB),负中(NM),负小(NS),零(ZO),正小(PS),正中(PM),正大(PB)。根据传统PI控制器仿真结果可知,误差e变化范围为[-100,600],根据式(17)将误差范围转换到(-3,3)上:

式中:x为真实测量值;l1,l2为转化前的范围上下界;2n为模糊化后模糊论域的长度;x′为模糊化后模糊论域。参数代入公式计算,得到误差变化率变化范围为[-6×1014,6×1014],因此误差变化率量化因子为5×10-15,各模糊变量均服从三角形隶属度函数分布[17-18],如图7所示,横坐标表示模糊论域,纵坐标表示隶属度函数值。

图7 三角形隶属度函数曲线分布图
各模糊变量的隶属函数表相同,表1为e的隶属函数表。表中:F为模糊变量;u为隶属度;e为模糊论域。
2.3 模糊控制规则
当模糊PI参数在线自整定时,模糊控制器不同的输入对应不同的输出,应当满足的规则如下:
(1)当|e|较大时,应该取较大的Kp,取较小的Ki以使系统能快速响应,同时防止积分饱和;
(2)|e|中等大小时,e与ec同号表示被调量将会朝着偏离给定的方向变化,此时应取较大的Kp和Ki;当e和ec异号时,表示被调量朝着给定方向变化,此时应减小Kp和Ki值[19];

表1 e的隶属函数
(3)当|e|接近零时,为了提高系统稳态性能,应该增大Kp和Ki的值。
根据上述规则,可得出ΔKp和ΔKi模糊关系表,如表2和表3所示。

表2 ΔKp的关系表

表3 ΔKi的关系表
2.4 模糊推理与输出变量的解模糊
模糊控制中的语句采用If e is A and ecis B then ΔKpis C and ΔKiis D的形式。其中A,B,C,D∈ {NB,NM,NS,ZO,PS,PM,PB}为模糊集。
对于每张控制规则表,由多段蕴涵模型处理:

其中

由此计算出R(1)和R(2),由极小极大法有:

将各对输入模糊变量代入式(21),计算出模糊控制决策u,采用面积质心法进行模糊信息的判决(解模糊),得到输出变量的精确值[20]。把论域U上将μU′(u)曲线与横坐标围成区域的面积平分为两部分的元素u∗作为系统的确切响应量,有

式中:u为输出变量的模糊值;μU′(u)为对应的隶属度。
根据上述理论分析,在Matlab/Simulink环境下建立模糊PI控制器仿真模型,如图8所示。
3 仿真与结果分析
根据前面建立的串联式电传动系统各部分的模型,并采用模糊自整定PI控制算法,搭建串联式电传动系统的仿真模型,如图9所示,主要由发电机、发电机控制模块、整流器、逆变器、驱动电机控制模块和驱动电机构成。图10为基于模糊PI的母线电压控制模块。

图8 模糊PI控制器仿真模型

图9 串联式电传动系统仿真模型
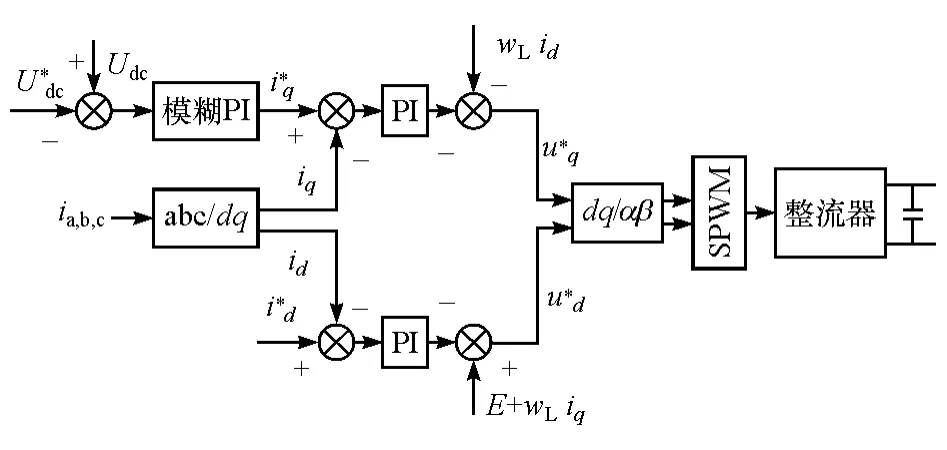
图10 基于模糊PI的直流母线电压控制
模型中所用的发电机和驱动电机采用相同的电机,其参数如表4所示。
系统中发电机参考转速为2 000r/min,驱动电机参考转速为1 000r/min,采样周期Ts=10-6s,最大仿真步长为10-6s,仿真时间为0.5s,在0.2s时驱动电机空载启动;0.3s时,负载转矩从0突变到100N·m;在0.4s时负载转矩从100N·m突降为0。仿真结果如图11和图12所示,其中图11为传统PI控制下的直流母线电压变化波形,图12为模糊自适应PI控制下的直流母线电压波形。母线电压波动和稳定时间如表5所示。

表4 电机参数

图11 传统PI直流母线电压波形

图12 模糊自适应PI直流母线电压波形

表5 母线电压波动及稳定时间
从表5可以看出,驱动电机空载启动时,模糊自适应PI与传统PI相比,母线电压波动从40降为27V,降低了32%,调整时间从0.07降为0.05s,降低了29%;0.3s加载时,母线电压波动从40降为24V,降低了40%,调整时间从0.06降为0.03s,降低了50%;0.4s负载降为0时,母线电压波动从36降为19V,降低了47%,调整时间从0.08降为0.04s,降低了50%。
图13和图14分别为采用传统PI控制和自适应PI控制模式下前后功率链功率跟随情况,其中P1为前功率链功率,P2为后功率链功率。
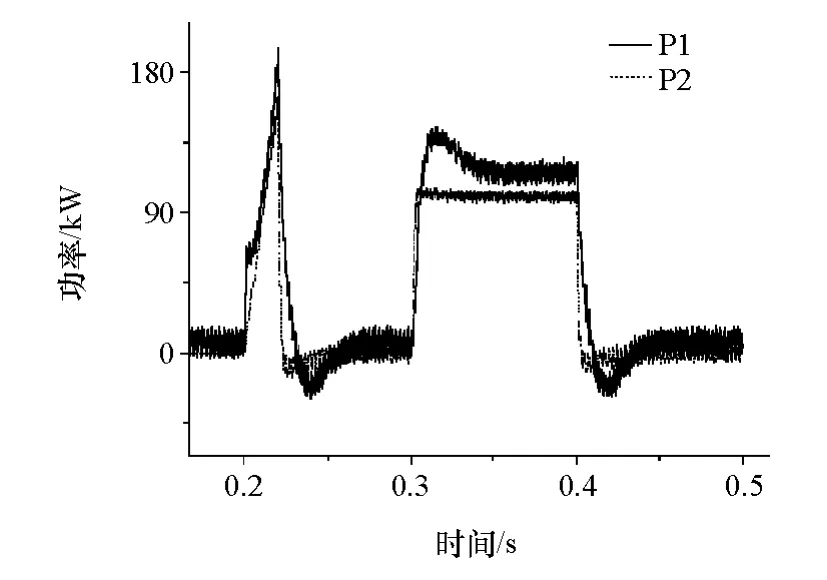
图13 传统PI前后功率链功率变化情况

图14 模糊自适应PI前后功率链功率变化情况
图13 和图14反映了使用不同PI时前后功率链的变化情况。0.2s时,驱动电机启动,在PI的调节下,输出功率迅速增大,驱动电机运转稳定后,由于负载转矩为零,输出功率很快降为零;0.3s时突加100N·m负载转矩,输出功率迅速增加;0.6s时负载转矩降为零,输出功率迅速降为零。对比图13和图14可以看出,模糊自适应PI控制策略能够更好地使前功率链跟随后功率链的变化,使母线电压的波动减小,加快了系统的响应速度。
图15和图16分别为采用传统PI控制和模糊自适应PI控制下的驱动电机输出转矩波形,由于本文中提出的控制策略针对整流侧,因此不同控制模式下驱动电机输出转矩无大的变化,但新的控制策略仍能继续保持输出转矩脉动较小、响应较快的特点。

图15 传统PI驱动电机输出转矩波形

图16 模糊自适应PI驱动电机输出转矩波形
4 结论
与传统PI控制相比,本文中提出的模糊PI控制方法能在线调整PI参数,更大幅度地改变调节量,能更快速地抑制电压的波动;当负载发生变化时,既能减小直流母线电压下降的幅度,又能更快地使母线电压恢复到期望值。仿真结果表明,模糊PI控制器使响应时间缩短了50%,超调量降低了55%,使系统有更好的鲁棒性和动态性能,在提高系统响应速度的同时,不影响转矩的输出。该模型对于取消串联式电传动车辆的储能单元,降低成本,提高系统可靠性具有重要理论指导意义和应用价值。
[1] 杜新,朱凌.基于功率前馈的直流母线电压控制方法研究[J].电力科学与工程,2013(8):6-9,26.
[2] 刘波,金昊.永磁直驱风电系统双PWM变换器前馈补偿控制[J].电力系统保护与控制,2014(15):52-57.
[3] 李光叶.双PWM变换器协调控制研究[D].天津:天津大学,2011.
[4] 万健如,宫成,李昆鹏.电压型PWM整流器预测直接电容功率控制研究[J].电力系统保护与控制,2013(3):96-101.
[5] 吴忠强,马宝明,孔启翔.基于Hamilton系统的风力发电双PWM变流器控制研究[J].电力系统保护与控制,2012(17):19-23,29.
[6] 罗林,张桂怀,王振凯.风力发电用双PWM变频器仿真研究[J].电气技术,2009(8):58-61.
[7] 皇金锋.全桥式DC/AC/DC变换器的建模与仿真[J].计算机仿真,2013(4):336-338,343.
[8] 倪靖猛,方宇,邢岩,等.基于优化负载电流前馈控制的400Hz三相PWM航空整流器[J].电工技术学报,2011(2):141-146,164.
[9] 徐向丽,王鸣翔.主从控制模式下并联Buck变换器的均流技术研究[J].信息技术,2014(1):98-100.
[10] 戴鹏,朱方田,朱荣伍,等.电容电流直接控制的双PWM协调控制策略[J].电工技术学报,2011(S1):136-141.
[11] 王明渝,代同振,吴喜红,等.双PWM变换器功率前馈控制策略仿真研究[J].系统仿真学报,2012(4):892-896.
[12] 李爱平,邓海洋,徐立云.基于模糊PID的永磁同步电机矢量控制仿真[J].中国工程机械学报,2013(1):25-30,40.
[13] 姜卫东,李王敏,佘阳阳,等.直流电容储能反馈和负载功率前馈的PWM整流器控制策略[J].电工技术学报,2015(8):151-158.
[14] 陈修亮,车倍凯.永磁同步电机矢量控制解耦方法的研究[J].电气技术,2013(4):37-40,43.
[15] 郑连清,池俊锋,陆治国.基于三级模糊自适应PI控制的VSCHVDC控制器设计[J].电力系统保护与控制,2011(23):117-122,127.
[16] 乔海.基于FPGA的永磁同步电机模糊控制研究[D].哈尔滨:黑龙江大学,2013.
[17] 颜永民,张国强.自适应模糊PID控制器的研究[J].建筑热能通风空调,2014(1):29-32.
[18] 王述彦,师宇,冯忠绪.基于模糊PID控制器的控制方法研究[J].机械科学与技术,2011(1):166-172.
[19] 王顺杰,王润田.在线自适应模糊PID控制器的设计与仿真[J].化工自动化及仪表,2012(8):975-978,981.
[20] 赵笑笑.基于模糊理论与常规PID控制的模糊PID控制方法研究[J].山东电力技术,2009(6):54-56,63.
A Study on Robust Control of DC Bus Voltage for Series Electric Drive Vehicles Without Energy Storage Unit
Song Qiang1,2,Li Song1,2&Saeid Habibi3
1.School of Mechanical Engineering,Beijing Institute of Technology,Beijing 100081;2.Collaborative Innovation Center for Electric Vehicles,Beijing 100081; 3.McMaster University,Hamilton,Toronto,Canada L8S4L8
In view of that energy storage unit(ESU)in conventional series electric drive system results in the defects of large volume,high cost and low life span,a series electric drive system without ESU is proposed,and aiming at the issue of bus voltage fluctuation caused by ESU elimination,fuzzy control is added on the basis of traditional voltage/current dual closed-loop PI control,a DC bus voltage control strategy for fuzzy adaptive PI control is formulated and an online self-tuning scheme for PI parameters is put forward.A model for series electric drive system without ESU is established with Matlab/Simulink and a simulation is conducted on the model and control strategy.The simulation results show that the fuzzy adaptive PI control strategy is conducive to increasing the response speed of system,reducing voltage overshoot and enhancing the robustness of system with better static and dynamic performances.
series electric drive system;energy storage unit;DC-bus voltage;fuzzy adaptive PI control;robustness
10.19562/j.chinasae.qcgc.2017.08.013
∗国家国际科技合作专项(2014DFG70840)资助。
原稿收到日期为2016年6月20日,修改稿收到日期为2016年10月25日。
宋强,副教授,E-mail:songqiang@bit.edu.cn。
