基于谐波小波包和BSA优化LS-SVM的铣刀磨损状态识别研究
2017-09-14董彩云张超勇孟磊磊肖鹏飞林文文
董彩云 张超勇 孟磊磊 肖鹏飞 罗 敏 林文文
1.华中科技大学机械学院数字制造装备与技术国家重点实验室,武汉,4300742.湖北汽车工业学院电气与信息工程学院,十堰,4420023.宁波大学机械工程与力学学院,宁波,315211
基于谐波小波包和BSA优化LS-SVM的铣刀磨损状态识别研究
董彩云1张超勇1孟磊磊1肖鹏飞1罗 敏2林文文3
1.华中科技大学机械学院数字制造装备与技术国家重点实验室,武汉,4300742.湖北汽车工业学院电气与信息工程学院,十堰,4420023.宁波大学机械工程与力学学院,宁波,315211
针对铣削刀具磨损状态识别问题,提出谐波小波包和最小二乘支持向量机(LS-SVM)的状态识别方法。为克服传统小波包分解的频带交叠问题,采用谐波小波包提取不同磨损状态下铣削力信号的各频段信号能量,归一化处理后,输入LS-SVM多类分类器,实现铣削刀具磨损状态的识别。针对LS-SVM的惩罚因子和核参数对模型识别精度影响较大的问题,提出回溯搜索算法(BSA)进行自动参数寻优。实验结果表明,谐波小波包比小波包在刀具磨损状态特征提取时具有更好的识别效果。与粒子群算法进行比较,证明BSA优化LS-SVM具有更高的识别精度。
刀具磨损;谐波小波包;回溯搜索算法;最小二乘支持向量机
0 引言
刀具智能状态监测技术在先进制造生产中具有重要意义。刀具磨损在线监测作为其主要内容,可以保证产品质量,提高生产效率,降低生产成本,缩短生产时间,避免因刀具失效造成的零件加工表面精度低、零件报废、机床故障等问题,对加工过程自动化具有重要作用。国内外有许多学者研究了刀具磨损智能监测和刀具寿命预算方法,如TETI等[1]与ROTH等[2]概括了刀具磨损状态监测技术在传感信号选择、信号处理与模式识别等方面的发展现状。
目前刀具磨损状态监测的方法主要是间接法,通过引入模式识别的间接测量方法实现高准确率快速识别[3]。间接法监测过程大致分为信息采集、特征提取、状态识别、决策控制四个阶段,其中特征提取和模式识别阶段尤为关键。
信号特征提取方法有时域法、频域法、时频域法、时间序列分析、分形特征等。时域和频域法都不能兼顾信号的时域和频域中的总体和局部变化,不能合理地处理非平稳信号。时频域法包括STFT、小波分析、HHT等。文献[4]研究了小波分析技术在刀具磨损状态识别中的应用。文献[5]研究了小波包特征提取技术在钛合金车削刀具磨损状态监测中的应用。文献[6]利用分形理论对刀具磨损信号进行处理,发现切削力动态分量的分形维数和刀具磨损状态具有很强的相关性。文献[7]采用具有严格盒形谱特性的谐波小波包,能够将信号不交叠且无遗漏地分解到不同的频段,获得信号在不同频段上的特征信息。谐波小波具有优良的滤波特性,在微弱信号、突变信号等非平稳信号特征提取中具有很强的优势[8-9]。文献[10-13]研究了谐波小波在振动信号、弱信号、碰摩故障以及旋转机械故障等方面的应用,均取得了很好的效果。
在模式识别方面,文献[14-16]研究了最小二乘支持向量机(least squares support vector machine,LS-SVM)在刀具磨损状态监测中的应用,证明了该方法与其他算法相比,具有更高的识别精度,由于LS-SVM的模型参数对其识别精度有较大影响,不同参数下的刀具磨损量识别精度差别大,故如何选择合适的惩罚因子和核参数在模式识别中非常关键。文献[17]通过改进的粒子群优化算法对最小二乘支持向量机的惩罚因子和径向基核函数参数进行了优化选择,对车刀磨损量进行模式识别,通过与标准粒子群算法优化的模型对比,发现识别误差更小,收敛更快。文献[18] 采用回溯搜索算法(backtracking search optimization algorithm,BSA)对多对不同Benchmark函数进行测试,与PSO、ABC等算法对比,证明了该算法操作简单,在全局搜索能力和收敛速度上占优。本文尝试利用BSA与LS-SVM相结合的模式识别方法进行铣刀刀具磨损状态识别,BSA用于优化LS-SVM的惩罚因子和核参数。特征提取结果分为两组,一组用于输入LS-SVM中进行训练,得到优化后的模式识别模型,另一组用于刀具磨损状态检测。
1 刀具磨损机理
1.1刀具磨损形式
切削时由于切屑和刀具前面、加工表面与刀具后刀面之间会产生持续的热量并存在摩擦,造成刀具的磨损。刀具磨损分为正常磨损(前刀面磨损、后刀面磨损、前后刀面同时磨损)和非正常磨损(脆性破损、塑性破损)。
1.2刀具磨损过程
刀具磨损量会随切削时间变化而逐渐变大,磨损的快慢与加工条件、加工材料有关。刀具磨损过程在不同条件下基本类似,一般典型的刀具磨损曲线图见图1,刀具磨损过程一般分为初期磨损(Ⅰ)、正常磨损(Ⅱ)和急剧磨损(Ⅲ)三个阶段。
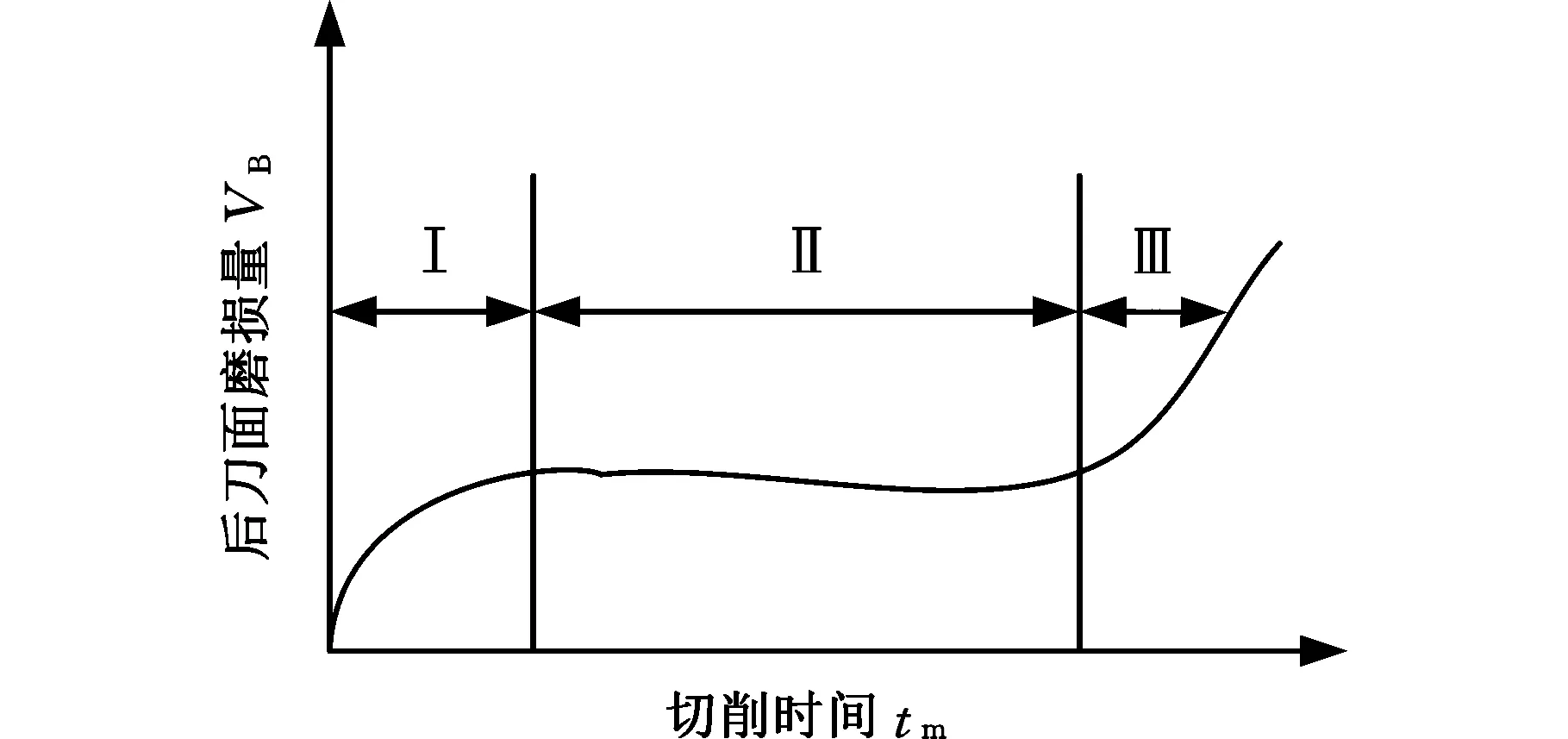
图1 刀具磨损曲线Fig.1 Tool wear curve
球头铣削力模型通常都是基于刀具坐标系建立的,原点设定为刀尖点位置,有三个方向的切削分力(Fx,Fy,Fz)。切削力作为与刀具在加工时的磨损、破损状态关系非常密切的物理特征,磨损量增大会导致切削力增大,刀具破损则引起切削力突变,所以对切削力变化的监测能够间接反映刀具磨损的状态。对切削力造成影响的原因比较多,如:工件的材料、切削用量和刀具几何参数,但是刀具的材质、是否选用切削液对刀具的磨损也有影响。
2 谐波小波变换
2.1谐波小波的概念
谐波小波具有严格的矩形频谱,频域表达式为
(1)
(2)
(3)
谐波小波的时域表达式为
ψ(t)=ψe(t)+iψo(t)=
(exp(i4πt)-exp(i2πt))/(i2πt)
(4)

ψ(t)的实部和虚部如图2所示,可以看出,谐波小波的实部是偶函数,虚部是奇函数,由信号分析理论可知,谐波小波具有“锁定”信号相位的功能[19]。

图2 谐波小波的实部和虚部Fig.2 Real and imaginary parts of harmonic wavelet
对谐波小波基进行伸缩、平移则可生成L2(R)空间的规范正交基,也即谐波小波函数族:
ψ(t)=[exp(i4πt(2j-k))-
exp(i2πt(2j-k))]/[i2πt(2j-k)]
(5)
其中,j为收缩因子,反映了谐波小波的分解层数,j∈Z;k为平移因子。j=0时,在频域内谐波小波只在2π~4π内有值,在第j层时只在2j+1π~2j+2π有值。谐波小波频谱分布如图3所示。

图3 谐波小波频谱分布Fig.3 Harmonic wavelet spectrum distribution
2.2广义谐波小波
由图3可知,谐波小波同传统小波一样,频率分辨率在低频时高,在高频时低。但是对实际信号进行分析时,同样需要在高频时具有较高分辨率,因此NEWLAND[7]构造出了广义谐波小波。
取谐波小波每层的频率段ω=[2πm,2πn],则谐波小波的频域表达式为
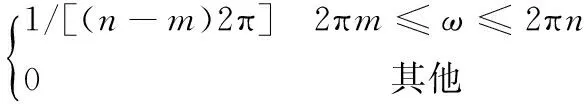
(6)
其中,m,n满足:

m值取2j,j=0,1…,N-1,N为分解层数。
对式(6)进行逆傅里叶变换可以得到时域表达式:
ψm,n(t)=[exp(i2πtn)-exp(i2πtm)]/[i2πt(n-m)]
(7)
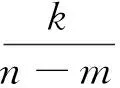
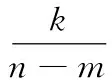
(8)
式(8)就是频率带宽为2π(n-m)、时间中心为k/(n-m)的广义谐波小波的一般形式。可以看出:不同频带所对应的小波是相互正交的,相同频带(k≠0时)对应的小波也是相互正交的。以谐波小波系数ψ(t)作为L2(R)的一组正交基,对信号f(t)进行谐波小波分解,就可以将信号分解到相互独立的频段,能量较弱的细节信号也能准确地显现出来,有利于信号特征的提取。
对于离散信号f(t),t=0,1,…,N-1,广义谐波小波变换的时域表达式为
(9)
对式(9)进行离散傅里叶变换,则可得到频域表达式:
(10)
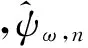
2.3谐波小波包
由式(8)可知,参数m、n决定了小波函数的带宽和频带中心的位置,可以通过调节m、n的值来调节谐波小波的带宽和中心频率,从而在任意分解层上将信号分解到不同的频段,实现谐波小波包变换,文献[7,19]给出了谐波小波包变换实现的具体过程。
3 回溯搜索算法优化LS-SVM基本理论
3.1LS-SVM基本原理
支持向量机(support vector machine,SVM)是VAPNIK等[20-21]根据统计学中的结构风险最小化原则提出的一种机器学习方法,其基本原理是寻找一个使分类间隔最大化的最优分类面。针对非线性问题,SVM引入核函数,将输入数据变换到高维空间,从而实现对问题的线性分类。SVM对小样本、非线性、高维数等问题同样可以获得较好的分类效果。
LS-SVM是标准SVM的变形,是将SVM求解二次规划问题转换成求解线性方程组,同时省去了不敏感损失系数,使算法复杂程度大大降低[22]。用于分类的LS-SVM算法的详细推导过程如下[23]。
给定N个训练样本{(x1,y1),(x2,y2)…,(xN,yN)},其中xi为n维的训练样本输入,yi为训练样本输出,i=1,2,…,N,yik∈{-1,+1}。LS-SVM算法的目标优化函数为
(11)
i=1,2,…,N
式中,φ(·)为核函数,用来将输入样本映射到高维特征空间;ω为权矢量;ei为误差;b为偏置量;γ为惩罚因子。
LS-SVM优化问题对应的 Lagrange函数:
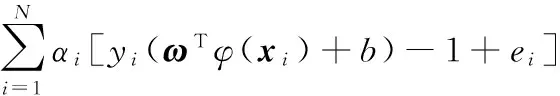
(12)
其中,αi为拉格朗日乘子,αi≥0。
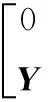
(13)
其中,Y=[y1y2…yN]T,1v=[11…1]T,α=[α1α2…αN]T,I为N×N阶的单位矩阵,Z=[y1φ(x1)y2φ(x2) …yNφ(xN)]T,核函数矩阵Ω=ZZT,Ωkl=ykylφ(xk)Tφ(xl)=ykylK(xk,xl),核函数K(xk,xl)是满足Mercer条件的对称函数。
LS-SVM的分类决策函数为
(14)
径向基(RBF)核函数是最常用的核函数K(x,xi)=exp(-‖x-xi‖2/σ2),σ为径向基函数的宽度。基于径向基核函数的LS-SVM,需确定惩罚因子γ和核参数σ两个参数。
LS-SVM方法本身是针对二分类问题而设计的,但是平时要解决的问题大多是多分类问题,因此文献[24]提出了将多分类问题转化为多个二分类问题的解决方案。目前常用的将多分类问题转化为多个二分类问题的方法主要有[25]:一对一方法(one versus one,1vs1)、一对多方法(one versus all,1vsA)、有向无环图方法(directed acyclic graph,DAG)、纠错输出编码方法(error-correlating output codes,ECOC)、最小输出编码(minimum output codes,MOC)等。
3.2回溯搜索算法
BSA是CIVICIOGLU[18]于2013年提出的一种新种群进化算法,该算法的流程和差分进化算法类似,但在变异操作(扰动策略)和交叉操作(混合策略)上,两者有本质的区别。BSA采用新型的扰动策略和混合策略,优化效率大大提高,该算法仅有一个控制参数(混合比例参数)使得操作更加简单。
BSA的算法流程有两次选择操作,可称为选择Ⅰ和选择Ⅱ[26-27]。选择Ⅰ用来选择历史种群,选择Ⅱ用于更新种群。它的算法流程可分为初始化种群、选择Ⅰ、变异、交叉、选择Ⅱ五部分。
(1)种群初始化。BSA的初始化包括两个种群的初始化,分别为种群Pop和历史种群oldPop,初始化按式(15)进行:
(15)
其中,i=1,2,…,popsize;j=1,2,…,D,popsize是种群规模,D是个体长度(问题维数),lowj、upj分别是第j维分量的最小值和最大值,U(·)表示均匀分布,Popi,j、oldPopi,j是(lowj,upj)上服从均匀分布的随机数,两次初始化操作相互独立。为了避免第一次执行选择Ⅰ操作时,oldPop值为空,这里对oldPop也进行了初始化,以保证算法的可行性。
(2)选择Ⅰ。BSA的选择Ⅰ用来为每一次迭代选择一个新的历史种群oldPop,其算法思想如下:
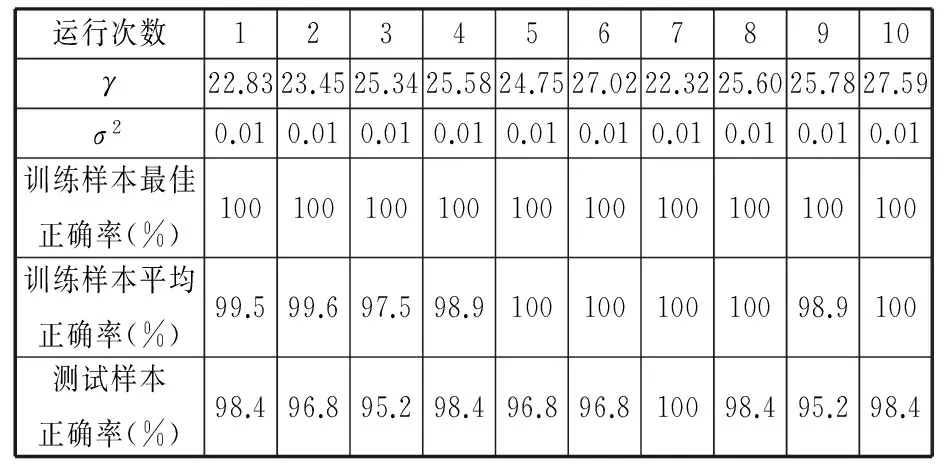
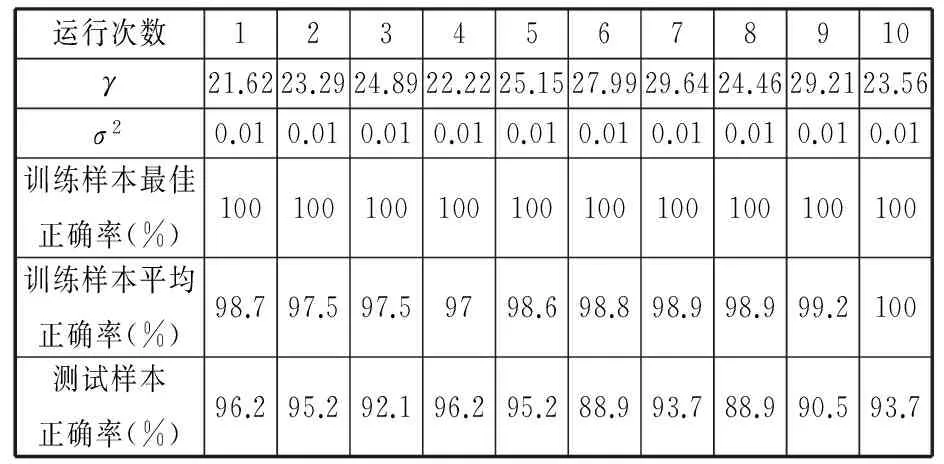
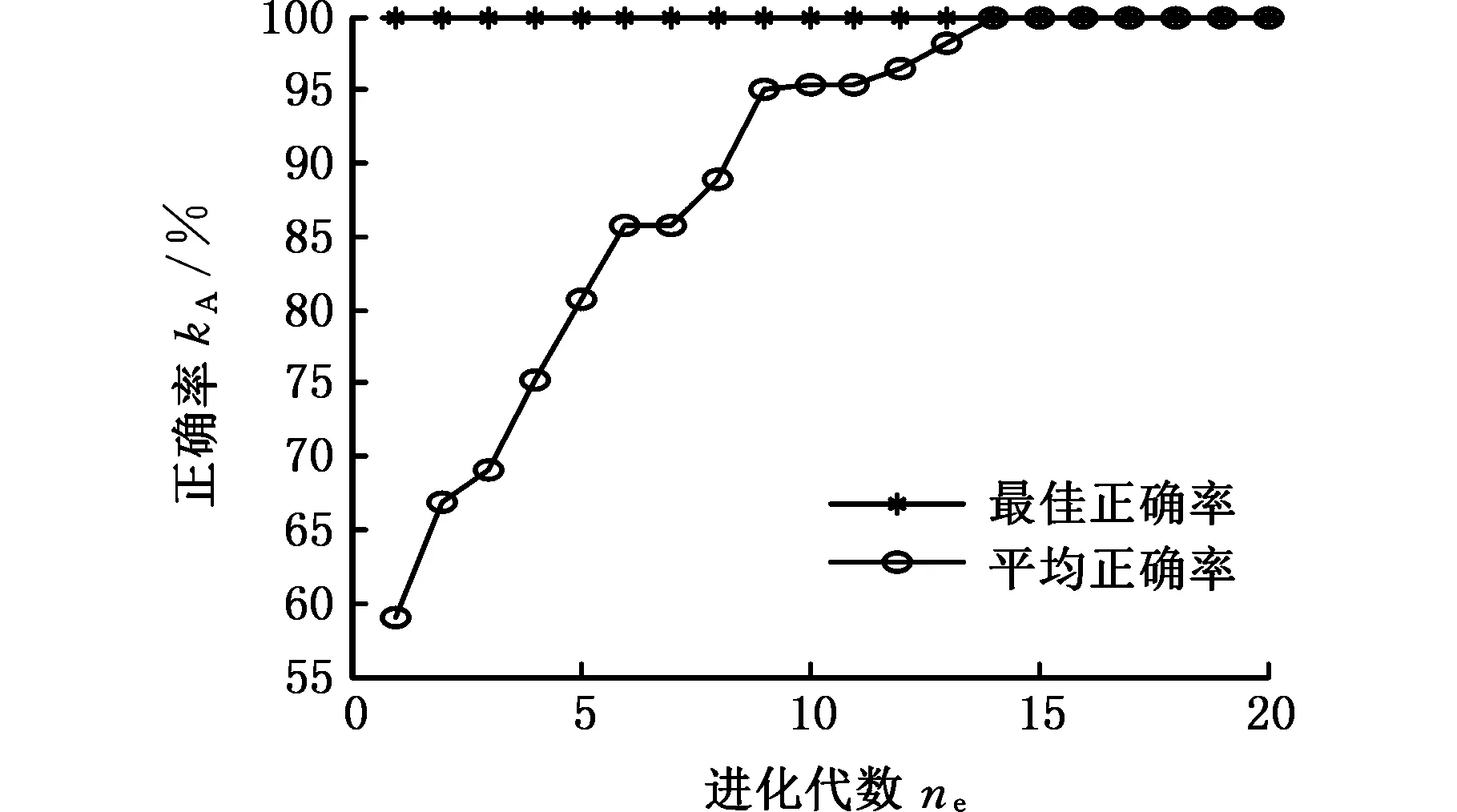
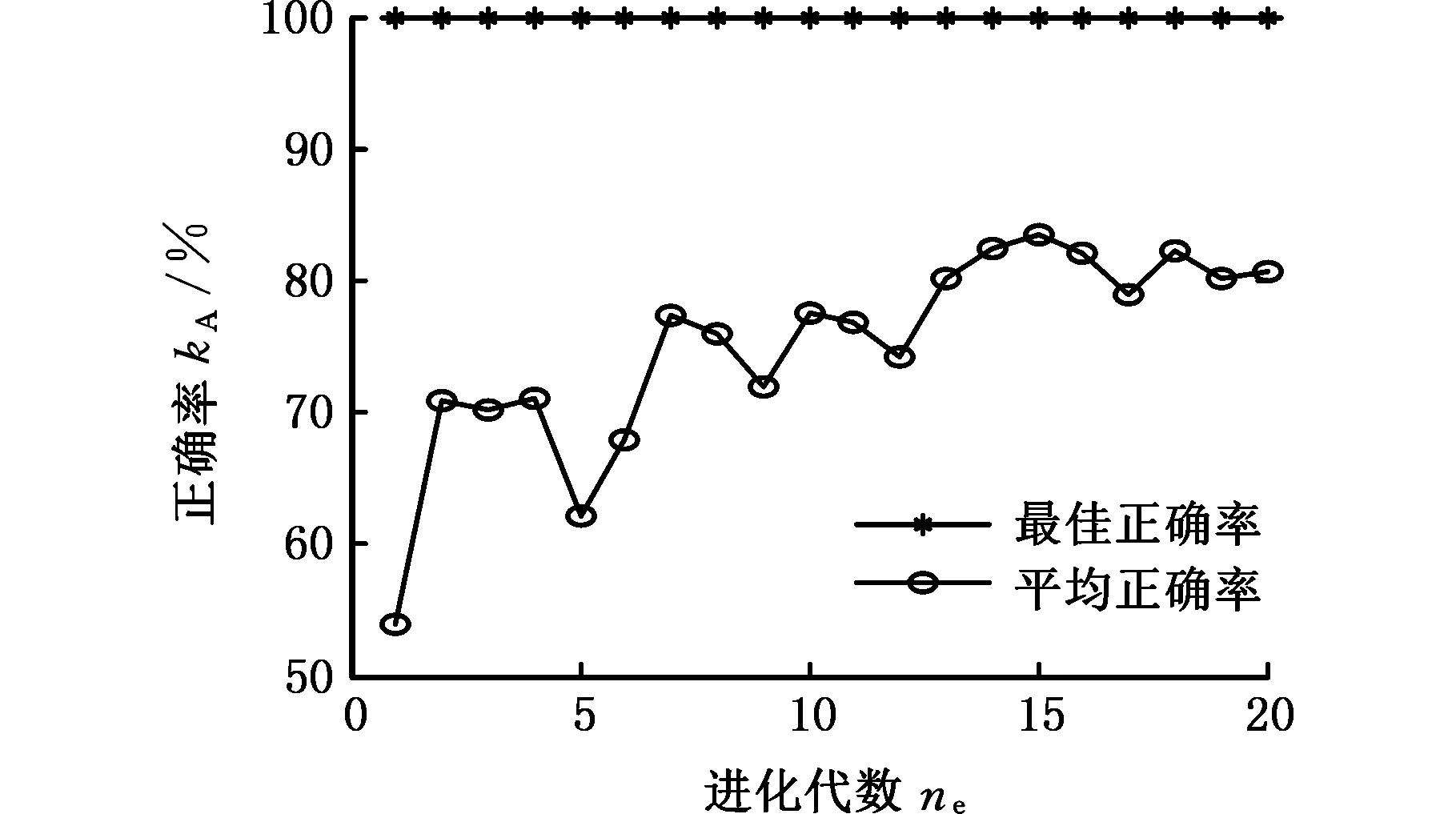
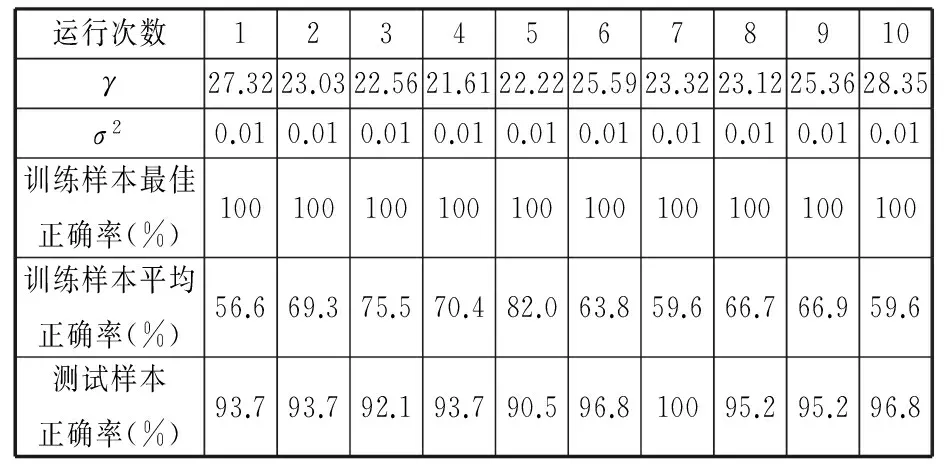
ifa (16) 式中,a、b为(0,1)上服从均匀分布的随机数。 (3)变异。在oldPop的值确定后,对oldPop中的个体进行随机排序,生成种群oldPop'。利用下式进行变异: Mutant=Pop+F(oldPop'-Pop) (17) 这里F是变异尺度系数,用以控制变异的程度;F=3rand(n),rand(n)是服从标准正态分布的随机数。 (4)交叉。BSA使用了一种新的种群交叉策略,通过设置混合比例参数mr来控制种群间交叉的粒子个数[28],具体表达式如下: (18) 其中,mapi,j为N×D的二元整数矩阵中的元素,元素初始赋值全为1,具体计算表达式如下: (19) (5)选择Ⅱ。通过贪婪选择机制,比较种群T与种群Pop对应位置的适应度,用T中所有适应度比Pop较好的个体代替Pop的对应位置个体,完成Pop的更新,一次迭代完成。选择Ⅱ如下式所示: (20) 记录当前最优解和对应的解向量,重复步骤(2)~步骤(5),直到满足循环终止条件,最后输出最优解。 3.3回溯搜索算法优化LS-SVM 本文提出运用BSA优化算法对LS-SVM的惩罚因子γ和核参数σ进行自动选择,以达到最佳组合值,使识别模型准确率达到最高。 假设已建立了系统的样本集{(x1,y1),(x2,y2),…,(xN,yN)},BSA优化LS-SVM过程中的LS-SVM模型的优劣采用最小分类错误率(minimal classification error rate,MCER)来衡量: (20) 式中,m1为被错误分类的样本数;N为训练样本数量。 如果在BSA优化过程中直接采用MCER作为适应度值,则可能会造成识别模型对训练样本的过拟合,但对于测试样本的泛化能力很差,从而失去了模型的实用性。为了提高识别模型的泛化能力,本文在参数优化时采用了K-折交叉验证(K-fold cross validation,K-CV),即在BSA的每次迭代过程中,对当前γ和σ所确定的LS-SVM进行交叉验证,将交叉验证的平均MCER作为BSA迭代的适应度值。 K-折交叉验证,即将训练样本分成K组(一般为均分),每个子样本集分别作为一次验证集,则可得到K个模型,用K个模型的平均分类错误率作为此K-CV下分类器的性能指标。K一般从3开始取。使用K-CV交叉验证方法,可以有效避免识别模型的过学习以及欠学习。 基于BSA优化LS-SVM的刀具磨损状态识别步骤如下:①提取特征向量,利用谐波小波包将铣削力信号分解到各个频段,提取各频段能量特征,并进行归一化处理,作为LS-SVM模型输入,刀具磨损状态类别序号作为输出。②初始化BSA种群,将LS-SVM的惩罚因子γ和核参数平方σ2作为每个个体的坐标值,用训练样本训练LS-SVM,并进行K-折交叉验证,计算种群的适应度f。③按照BSA流程进行迭代寻优。对每个个体,将适应度f(xi)与自身最优值进行比较,更新个体最优值;将个体最优值与种群(全局)最优值进行比较,更新种群最优值。④判断是否满足结束条件,若满足则输出最优化参数γ和σ2,若不满足则跳转到步骤②。结束条件一般设置为算法达到最大迭代次数、适应度小于给定精度等,本文以算法达到最大迭代次数为结束条件。⑤选出最优化参数γ和σ2,建立LS-SVM刀具磨损状态识别模型。⑥刀具磨损状态识别验证,利用测试样本检验模型识别能力。 4.1刀具磨损监测实验 试验数据来源于美国纽约预测与健康管理学会(Prognostic and Health Management Society,PHM)2010年高速数控机床刀具健康预测竞赛的开放数据。实验条件如表1所示。 表1 实验条件 试验在上述切削条件下重复进行6次全寿命周期试验。端面铣削材料为正方形,每次走刀端面铣的长度为108 mm且每次走刀时间相等,每次走刀后测量刀具的后刀面磨损量。试验监测数据有x、y、z三向铣削力信号,x、y、z三向铣削振动信号以及声发射均方根值。 本文选取第4组试验的x方向铣削力信号进行分析。本组试验总共315次走刀,每次走刀采样点数在220 000以上,为避免切入、切出的影响,本文提取每次走刀的50 001~100 000共50 000个数据点进行分析。 图4所示为第4组试验刀具磨损变化曲线,图中共有flute1、flute2、flute3、average四条曲线,分别表示x、y、z方向切削刃和其平均磨损情况,图中横坐标为走刀次数,纵坐标为后刀面磨损量。本文采用三个切削刃磨损量的均值来衡量球头铣刀的磨损情况。可以看出,前30次走刀为初期磨损阶段,30~225次走刀为正常磨损阶段,225次走刀后为急剧磨损阶段。 图4 球头铣刀磨损变化曲线Fig.4 Ball milling cutter wear curve 根据图4的铣削磨损情况,本文采用K均值聚类分析方法将磨损状态分为5类,状态1:1~30次走刀;状态2:31~130次走刀;状态3:131~200次走刀;状态4:201~260次走刀;状态5:261~315次走刀。 4.2谐波小波包频带能量敏感特征提取 (a)第15次走刀 (b)第80次走刀 (c)第165次走刀 (d)第240次走刀 (e)第270次走刀图5 走刀次数为15、80、165、240、270的x方向铣削力信号的原始信号Fig.5 Original signal of the x-direction milling force signal for 15, 80, 165, 240,270 feeding times (a)第15次走刀 (b)第80次走刀 (c)第165次走刀 (d)第240次走刀 (e)第270次走刀图6 走刀次数为15、80、165、240、270的x方向铣削力信号的频谱Fig.6 The frequency of the x-direction milling force signal for 15, 80, 165, 240,270 feeding times 对前8个频段分别求信号的能量: (22) j=1,2,…,8 式中,n为采样点数。 以这8个频段分别对应的能量值为元素可以构成一个特征向量:T=(E1,E2,…,E8),由于各频段能量数值大小相差比较大,对特征向量进行归一化处理: (23) 其中,E为总能量,T′=(E1/E,E2/E,…,E8/E),归一化特征向量的各元素为 0~1之间的数。 图7所示为对走刀次数为15、80、165、240、270的x方向铣削力信号分别进行 6层谐波小波包分解后得到的频段能量分布图。从图中可以发现,在不同磨损状态下的力信号在同一频段的能量存在差异,因此可将其作为LS-SVM的输入向量,对刀具磨损状态进行识别。 (a)第15次走刀 (b)第80次走刀 (c)第165次走刀 (d)第240次走刀 (e)第270次走刀图7 谐波小波包归一化频段能量分布图Fig.7 Harmonic wavelet packet normalized band energy distribution map 为了展示谐波小波包特征提取相对于小波包的优越性,将其与常规的小波包dB9的特征提取结果输入改进LS-SVM中进行状态识别,比较识别结果。图8所示为对走刀次数为15、80、165、240、270的x方向铣削力信号分别进行6层小波包分解后得到的前8个归一化频段能量分布图。图8中,频段3、5、6、7、8数值很小,且变化不大,为减少计算量,可忽略不计。最终特征向量T′=(E1/E,E2/E,E4/E)。 (a)第15次走刀 (b)第80次走刀 (c)第165次走刀 (d)第240次走刀 (e)第270次走刀图8 小波包归一化频段能量分布图Fig.8 Wavelet packet normalized band energy distribution map 图9为频段1、频段2、频段4的归一化能量分布随走刀数的变化趋势图。可以看出,谐波小波包能量分布和小波包能量分布虽然变化趋势相似,仍存在较大差异,且谐波小波包能量分布波动小。 4.3模型的训练和测试 本实验总共315次走刀,每次走刀取一个样本,总共315个样本,划分为5个状态(同4.1节),每种状态按80%为训练样本,20%为测试样本划分。状态1:训练样本24个,测试样本6个;状态2:训练样本80个,测试样本20个;状态3:训练样本56个,测试样本14个;状态4:训练样本48个,测试样本12个;状态5:训练样本44个,测试样本11个;则训练样本总共为252个,测试样本总共为63个。 (a)谐波小波包能量分布 (b)小波包能量分布图9 频段能量变化趋势Fig.9 Band energy trends 这一5分类问题,采用荷语鲁汶天主教大学编写的LSSVMlabv1.8版本工具箱,运行条件为:Dell台式机,Windows 7操作系统,双核英特尔i5处理器,8G内存,MATLAB 2014a。通过多次试验对比1vs1、1vsA、ECOC、MOC四种方法,发现四种方法的分类准确率差异很小,而运行速度相差比较大。由于MOC采用最小数目的两类分类器,只需要构建3个两类分类器,运行速度最快,因此,本文采用基于MOC编码的多分类LS-SVM来对刀具磨损状态进行识别。 确定了训练数据后,进行回溯搜索算法的初始化工作。进化代数为30;种群规模为20;混合比例参数mr=1;γ,σ2的最大值和最小值都为1000和0.01。为了避免过学习以及欠学习状态的发生,提高模型的泛化能力,采用3-CV交叉验证方法。 在参数一致的条件下,分别将谐波小波包特征提取结果与小波包特征提取结果输入优化后的LS-SVM中进行状态识别,图10为某次迭代过程,两种特征提取方法得到的种群的最佳正确率与平均正确率随进化代数的变化图。 (a)谐波小波包 (b)小波包图10 不同特征提取方法的最优正确率与平均正确率变化图Fig.10 The optimal accuracy and average correct rate with different feature extractians 从图10中可以看出,谐波小波包分析的平均正确率进化代数为16时达到最优,而小波包在20代之后达到最优,基于谐波小波包特征提取方法的状态识别结果能更快收敛达到最大平均正确率。但是一次迭代过程可能存在随机性,由于适应度函数的选择,达到最优值的解可能不止一个,同时由于LS-SVM的最佳γ,σ2的组合可能也不止一个,因此运行10次,每次迭代结束时对比结果。由表2和表3可知,10次运行结果中,σ2=0.01,γ∈[20,30],测试样本正确率存在区别。通过测试实验结果比较发现,表2和表3中训练样本最佳正确率都可以达到100%,而表2中的训练样本平均正确率和测试样本正确率都比表3的高,且表2中正确率都在95%以上,说明采用谐波小波包提取特征向量的方法比小波包的正确率更高。 表2 谐波小波包特征提取的识别结果 表3 小波包特征提取的识别结果 为了说明本文采用的回溯搜索算法在优化LS-SVM参数上的优越性,与粒子群优化算法进行对比。粒子群算法的参数、进化代数、种群规模、γ及σ2的最大化值、最小值与回溯搜索算法相同,迭代速度范围为[-0.2×1000,0.2×1000]。采用线性递减权重,ω的最大值和最小值分别为0.8和0.4,学习因子c1=c2=2,同样采用3-CV交叉验证方法。图11为某次迭代过程,两种算法的种群的最优正确率与平均正确率随进化代数的变化图。从图中可以看出,在测试样本分类的平均正确率上,BSA优化LS-SVM的状态识别模型可以达到100%,明显比PSO优化LS-SVM的模型效果更好,且收敛迅速。 (a)BSA优化 (b)PSO优化图11 不同优化算法的最优正确率与平均正确率变化图Fig.11 The optimal accuracy and average correct rate with different optimization algorithm 由于适应度函数的选择,达到最优值的解可能不止一个,同时由于LS-SVM的最佳γ,σ2的组合可能也不止一个,本文运行10次,每次迭代结束时对比结果。由表4和表5可知,10次运行结果中,σ2=0.01,γ∈[20,30],表4的测试样本正确率都在90%以上。经过10次试验对比,两种优化方法的群体最佳正确率都在20代以内达到最优,但是平均正确率BSA比PSO效果好得多。说明BSA在LS-SVM参数寻优方面更有优势,验证了采用BSA优化LS-SVM的状态模式识别方法具有较高的正确率。 表4 BSA优化LS-SVM结果 表5 PSO优化LS-SVM结果 本文提出了通过谐波小波包对铣削力信号进行分频段能量特征提取,并采用回溯搜索算法对LS-SVM参数进行寻优,对铣削刀具磨损状态进行识别的方法。实验结果表明,对于采用铣削力信号进行刀具磨损状态识别,利用谐波小波包提取不同频段能量,将归一化处理后样本作为LS-SVM的输入样本相比小波包提取特征具有较高的识别正确率。在LS-SVM参数寻优方面,通过对比回溯搜索算法和经典的粒子群优化算法,实验测试结果显示了回溯优化算法在LS-SVM参数寻优方面的优越性,以及对于铣削刀具磨损状态识别,将谐波小波包分解和回溯搜索算法优化的LS-SVM相结合的方法可以获得良好的效果。 [1] TETI R, JEMIELNIAK K, O’DONNELL G, et al. Advanced Monitoring of Machining Operations[J]. CIRP Annals—Manufacturing Technology,2010,59(2):717-739. [2] ROTH J T, DJURDJANOVIC D, YANG X, et al. Quality and Inspection of Machining Operations: Tool Condition Monitoring[J]. Journal of Manufacturing Science & Engineering, 2010, 132(4):575-590. [3] SNR D E D. Sensor Signals for Tool-wear Monitoring in Metal Cutting Operations—a Review of Methods[J]. International Journal of Machine Tools & Manufacture, 2000, 40(8):1073-1098. [4] 丛龙慧,韩玉杰.小波分析在刀具磨损状态检测中的应用[J].林业机械与木工设备,2009,37(4):51-52. CONG Longhui, HAN Yujie. Application of Wavelet Analysis in Tool Wear Status Detection[J]. Forestry Machinery & Woodworking Equipment, 2009,37(4):51-52. [5] 陈侃,傅攀,李威霖,等.钛合金车削加工过程中刀具磨损状态监测的小波包子带能量变换特征提取新方法[J].组合机床与自动化加工技术,2011(1):35-38. CHEN Kan, FU Pan, LI Weilin, et al. The Tool Wear Monitoring Based on SUB-WPA Feature Selection in Process of Titanium Alloy Machining[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2011(1):35-38. [6] 林颖, 刘亚俊, 陈忠. 基于分形理论和神经网络的刀具磨损监测[J]. 中国机械工程, 2004, 15(16):20-22. LIN Ying, LIU Yajun, CHEN Zhong. Tool Wear Detection Using Fractal Theory and Neural Network[J].China Mechanical Engineering, 2004, 15(16):20-22. [7] NEWLAND D E. Harmonic Wavelet Analysis[J]. Proceedings of the Royal Society A: Mathematical Physical & Engineering Sciences, 1993, 443:203-225. [8] NEWLAND D E. Wavelet Analysis of Vibration: Part 1—Theory[J].Journal of Vibration and Acoustics,1994,116(4):409-416. [9] NEWLAND D E. Wavelet Analysis of Vibration: Part 2—Wavelet Maps[J].Journal of Vibration and Acoustics,1994,116(4):417-425. [10] 高强,何正嘉.谐波小波及其时频剖面图在旋转机械诊断中的应用[J].西安交通大学学报,2000,34(9):62-66. GAO Qiang, HE Zhengjia. Application of Harmonic Wavelet and Its Time-frequency Profile Plot to Diagnosis of Rotating Machinery[J].Journal of Xi’an Jiaotong University,2000,34(9):62-66. [11] 陈洁,沈远彤,李宏伟.基于谐波小波的弱信号提取[J].信号处理,2005(增刊1):40-43. CHEN Jie, SHEN Yuantong, LI Hongwei. Applying Harmonic Wavelet Extracting Weak Signal[J].Signal Processing,2005(S1):40-43. [12] 万方义,许庆余.裂纹转子—滑动轴承系统动静件碰摩故障的谐波小波分析[C]//2002年全国振动工程及应用学术会议论文集.北京,2002:111-116. WAN Fangyi, XU Qingyu. Harmonic Wavelet Analysis on Cracked Rotor Sliding Bearing System with Rotor and Stator Rubbing[C]//Proceedings of the 2002 National Conference on Vibration Engineering and Application.Beijing,2002:111-116. [13] 肖忠会.谐波小波分析及其在旋转机械信号分析中的应用[J].风机技术,2001(1):43-46. XIAO Zhonghui. Harmonic Wavelet Analysis and Its Application to Analyzing Signals of Rotating Machinery[J].Compressor Blower & Fan Technology,2001(1):43-46. [14] 关山,王龙山,聂鹏.基于EMD与LS-SVM的刀具磨损识别方法[J].北京航空航天大学学报,2011,37(2):144-148. GUAN Shan, WANG Longshan, Nie Peng. Identification Method of Tool Wear Based on Empirical Mode Decomposition and Least Squares Support Vector Machine[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(2):144-148. [15] SHI D F, GINDY N N. Tool Wear Predictive Model Based on Least Squares Support Vector Machines[J].Mechanical Systems and Signal Processing,2007,21(4):1799-1814. [16] WIDODO A, YANG B S. Support Vector Machine in Machine Condition Monitoring and Fault Diagnosis[J].Mechanical Systems and Signal Processing,2007,21(6):2560-2574. [17] 李威霖,傅攀,张尔卿.基于粒子群优化LS-SVM的车刀磨损量识别技术研究[J].计算机应用研究,2014,31(4):1094-1097. LI Weilin, FU Pan, ZHANG Erqing. Application of Particle Swarm Optimization-Least Square Support Vector Machine in Tool Wear Monitoring[J].Application Research of Computers,2014,31(4):1094-1097. [18] CIVICIOGLU P. Backtracking Search Optimization Algorithm for Numerical Optimization Problems[J].Applied Mathematics & Computation,2013,219(15):8121-8144. [19] 张文斌,周晓军,林勇,等.基于谐波小波包方法的旋转机械故障信号提取[J].振动与冲击,2009,28(3):87-89. ZHANG Wenbin, ZHOU Xiaojun, LIN Yong, et al. Harmonic Wavelet Packet Method Used to Extract Fault Signal of a Rotation Machinery[J].Journal of Vibration and Shock,2009,28(3):87-89. [20] VLADIMIR N, VAPNIK V. Statistical Learning Theory[M].New York:Wiley,1998. [21] VAPNIK V.The Nature of Statistical Learning Theory[M].Dordrecht: Springer Science & Business Media,2013. [22] SUYKENS J A K, GESTEL T V, Brabanter J D, et al. Least Squares Support Vector Machines[J]. Euphytica, 2002, 2(2):1599-1604. [23] SUYKENS J A K. Least Squares Support Vector Machine Classifiers[J].Neural Processing Letters,1999,9(3):293-300. [24] HSU C W, LIN C J. A Comparison of Methods for Multiclass Support Vector Machines[J]. IEEE Transactions on Neural Networks,2002,13(2):415-425. [25] 董晓睿.基于支持向量机的多分类模型的研究和设计[D].南昌:南昌大学,2013. DONG Xiaorui. Research and Design of Multiclassification Model Based on Support Vector Machine[D]. Nanchang:Nanchang University,2013. [26] 王晓娟,刘三阳,田文凯.带高效变异尺度系数和贪婪交叉策略的回溯搜索优化算法[J].计算机应用,2014,34(9):2543-2546. WANG Xiaojuan, LIU Sanyang, TIAN Wenkai. Improved Backtracking Search Optimization Algorithm with New Effective Mutation Scale Factor and Greedy Crossover Strategy[J].Journal of Computer Applications,2014,34(9):2543-2546. [27] 田文凯.一种高效自学习性回溯搜索优化算法[J].电子科技,2015,28(2):41-45. TIAN Wenkai. Effective Self-learning Backtracking Search Optimization Algorithm[J].Electronic Science and Technology,2015,28(2):41-45. [28] 李牧东,赵辉,翁兴伟.具有广泛学习策略的回溯搜索优化算法[J].系统工程与电子技术,2015,37(4):958-963. LI Mudong, ZHAO Hui, WENG Xingwei. Backtracking Search Optimization Algorithm with Comprehensive Learning Strategy[J].Journal of Systems Engineering and Electronics,2015,37(4):958-963. (编辑王旻玥) StateRecognitionofMillingToolWearsBasedonHarmonicWaveletPacketandBSAOptimizationLS-SVM DONG Caiyun1ZHANG Chaoyong1MENG Leilei1XIAO Pengfei1LUO Min2LIN Wenwen3 1.State Key Lab of Digital Manufacturing Equipment & Technology,Huazhong University of Science and Technology,Wuhan,430074 2.School of Electrical and Information Engineering,Hubei Automotive Industries Institute,Shiyan, Hubei,442002 3.School of Mechanical Engineering and Mechanics,Ningbo University,Ningbo, Zhejiang,315211 Aiming at the problems of milling tool wear state recognitions, a state recognition method was proposed based on harmonic wavelet packet and LS-SVM. To overcome the band overlapping problems in traditional wavelet packet decompositions, the milling force signal energies of each bands were extracted in different wear states by harmonic wavelet packet, which were brought in multi-class LS-SVM classifier after normalizing, then the classification recognition of different cutting tool states was achieved. BSA was proposed to search the optimal values of the kernel functional parameters and error penalty factors which affected the precision of the LS-SVM significantly. Experimental results show that harmonic wavelet packet is more effective and feasible than wavelet packet, and the proposed milling tool wear recognition method has higher accuracy. tool wear; harmonic wavelet packet; backtracking search algorithm(BSA); least squares support vector machine(LS-SVM) 2016-09-13 国家自然科学基金资助项目(51575211,51421062);国家自然科学基金国际(地区)合作与交流项目(51561125002);湖北省自然科学基金资助项目(2014CFB348);高等学校学科创新引智计划资助项目(B16019) TH164 10.3969/j.issn.1004-132X.2017.17.011 董彩云,女,1993年生。华中科技大学机械科学与工程学院硕士研究生。主要研究方向为刀具磨损状态识别。张超勇(通信作者),男,1973年生。华中科技大学机械科学与工程学院副教授。E-mail:zcyhust@hust.edu.cn。孟磊磊,男,1991年生。华中科技大学机械科学与工程学院博士研究生。肖鹏飞,男,1993年生。华中科技大学机械科学与工程学院硕士研究生。罗敏,男,1967年生。湖北汽车工业学院电气与信息工程学院教授。林文文,男,1989年生。宁波大学机械工程与力学学院讲师。
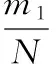
4 刀具磨损监测实验及特征提取
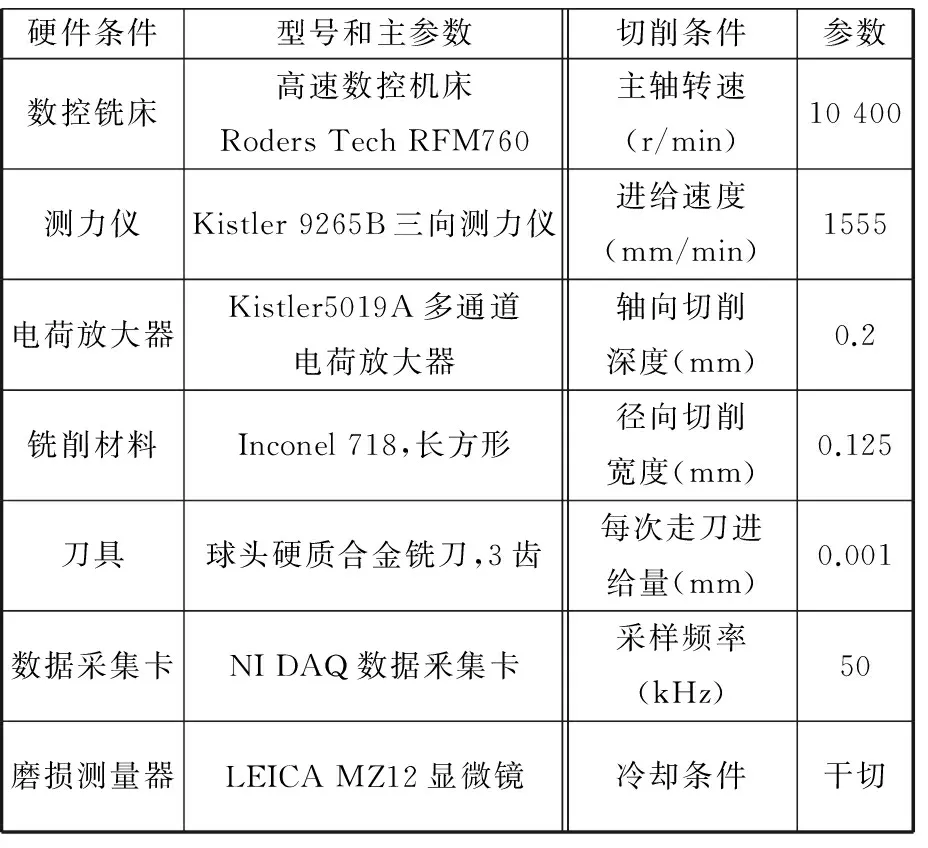

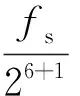
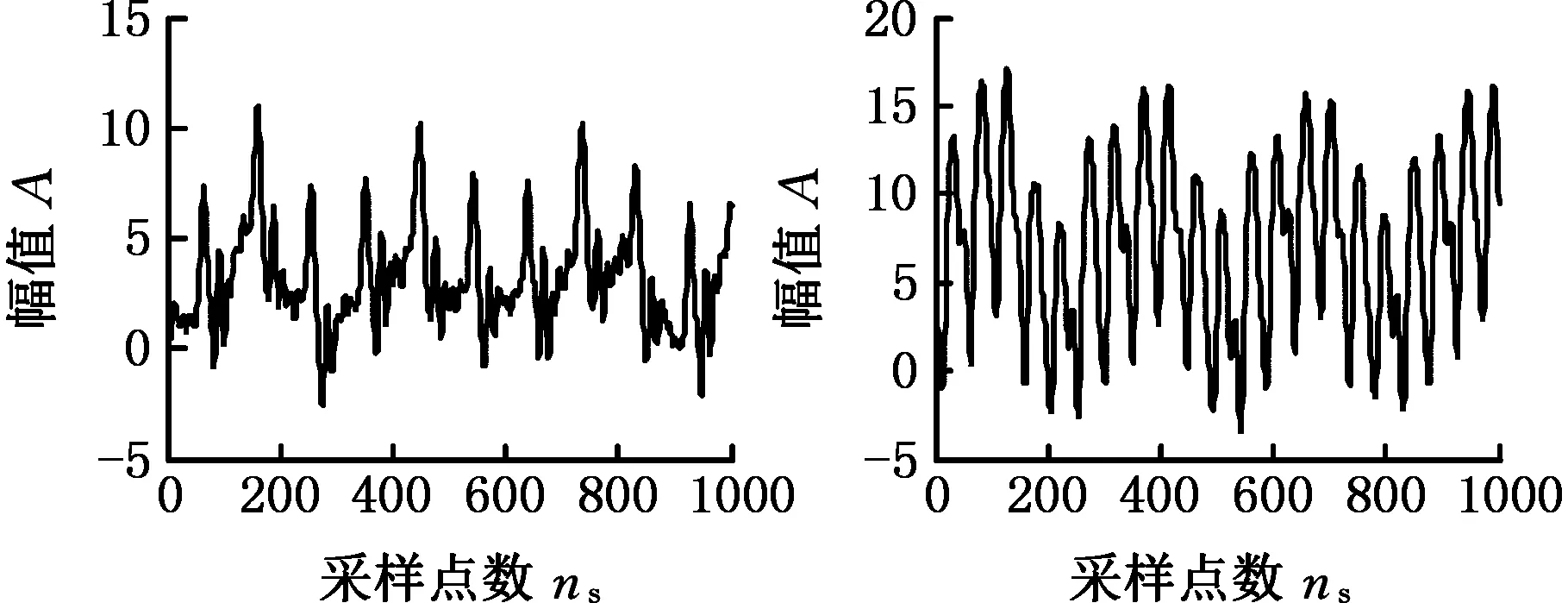

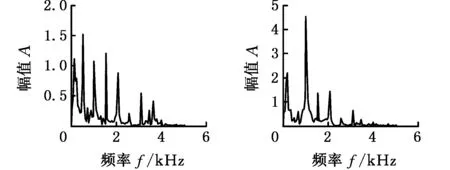
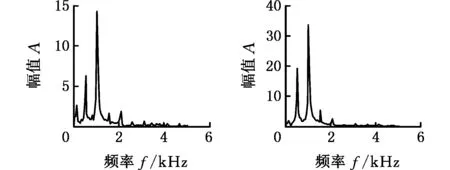

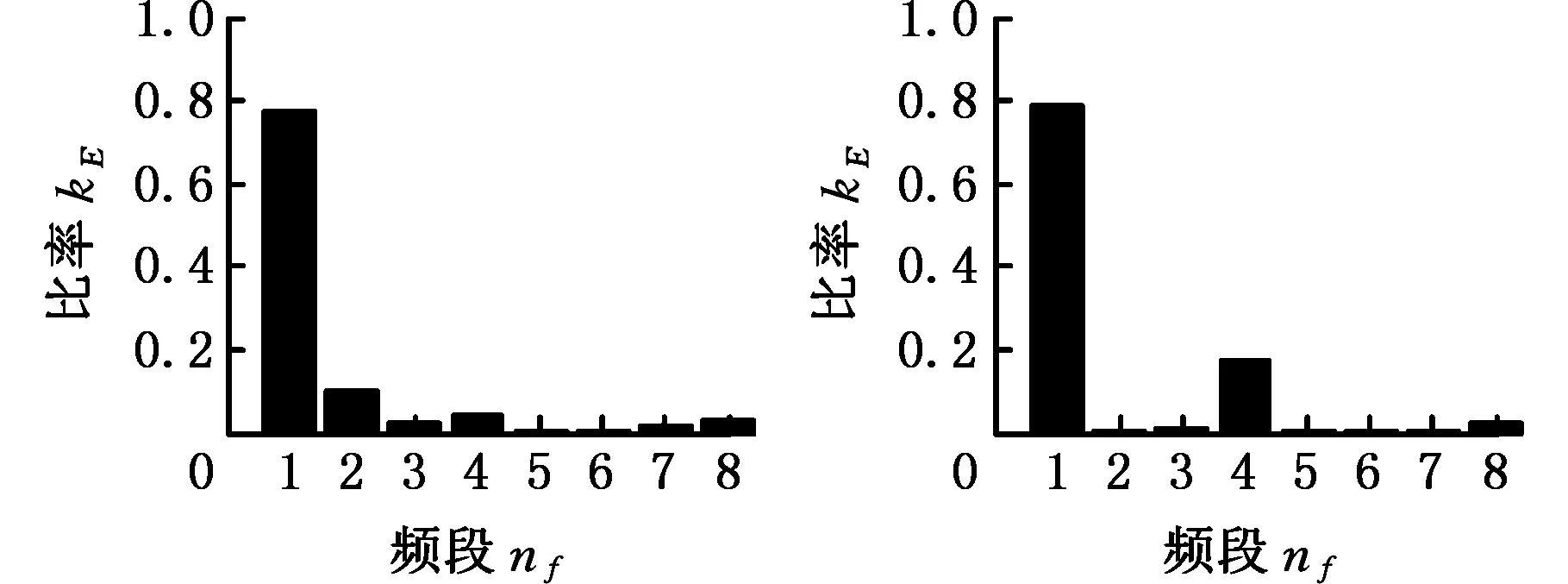


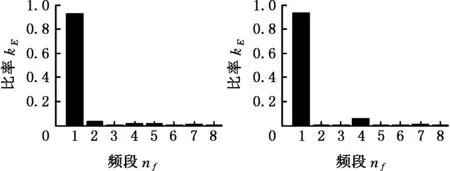
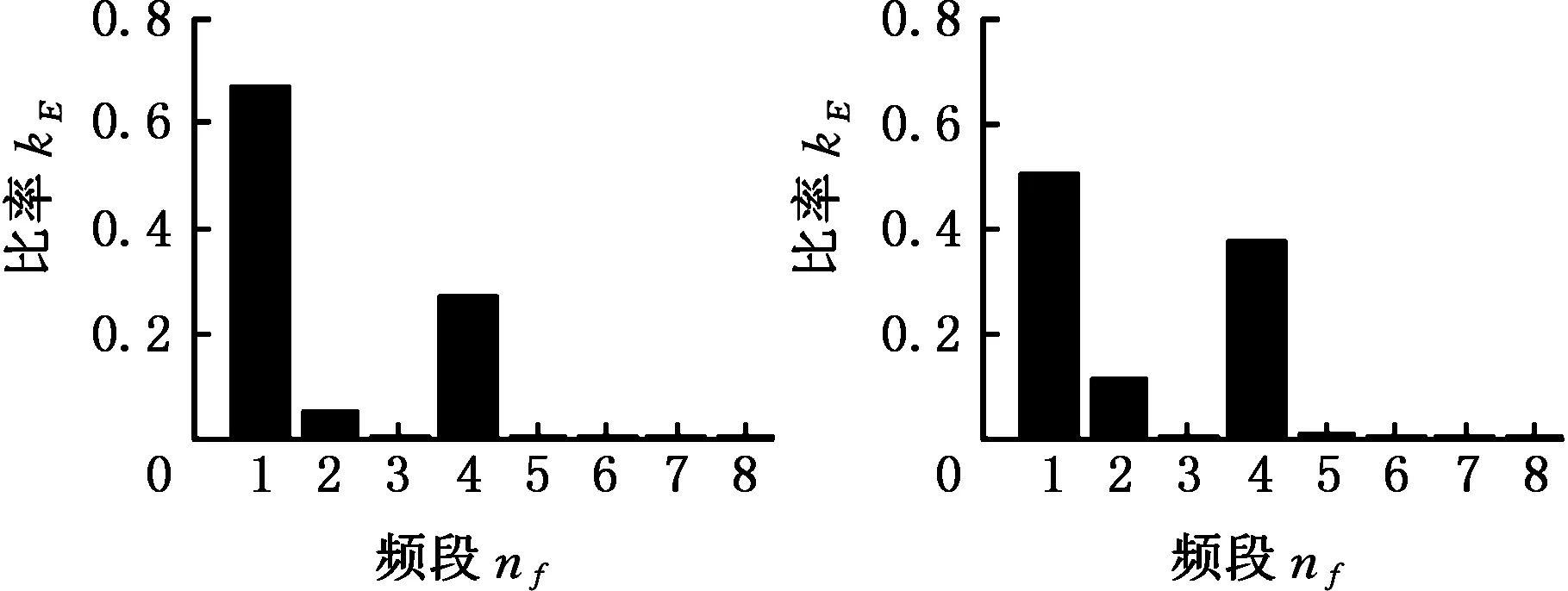

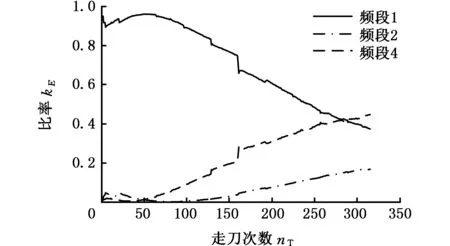
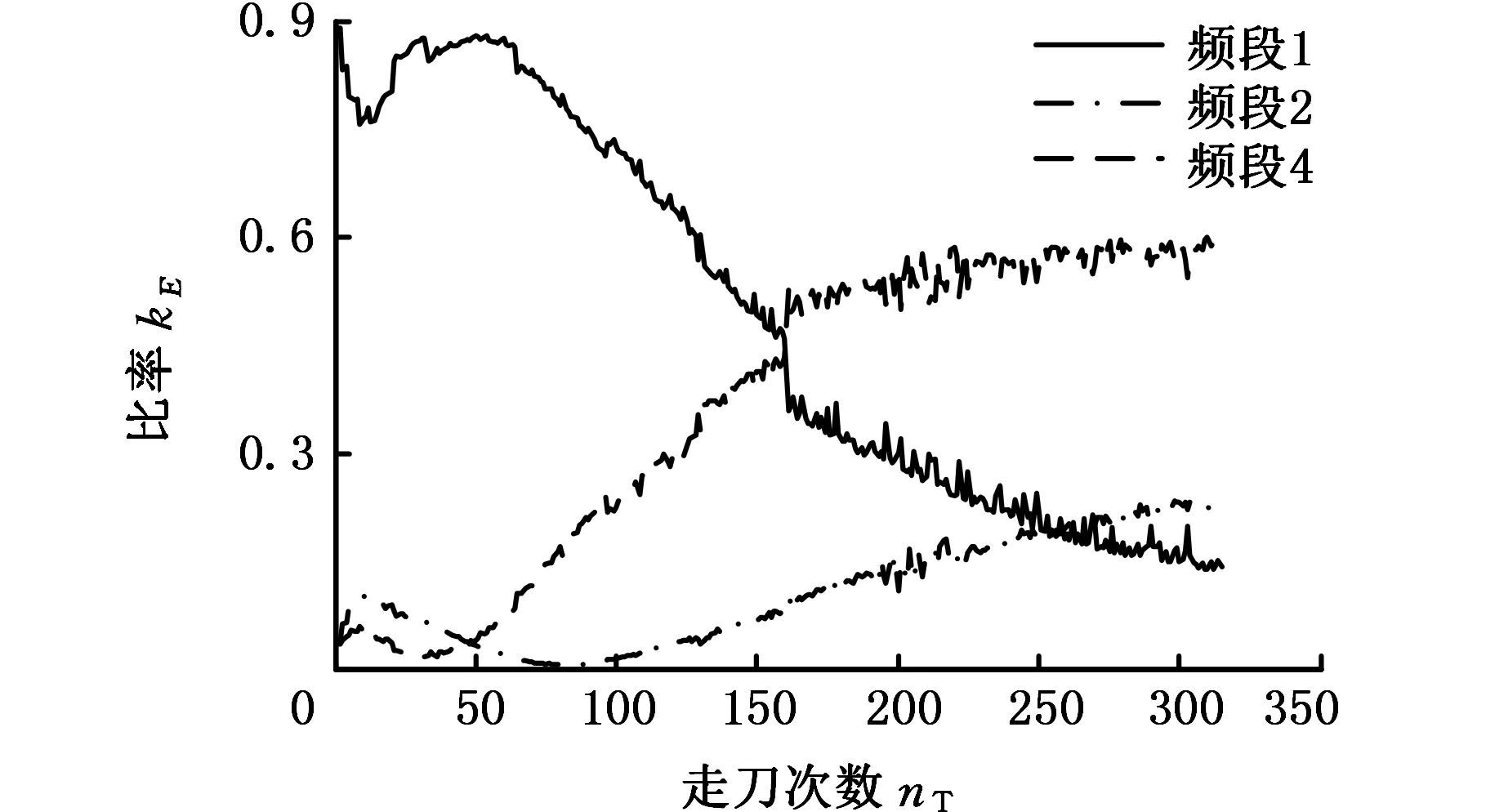

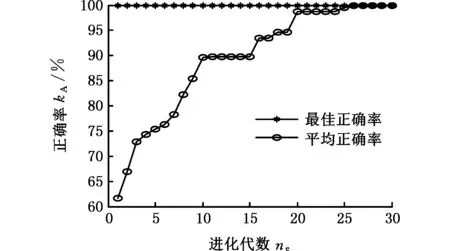

5 结论
