自励式电磁涡流联轴器调速性能研究

梅欣鑫 叶乐志 李德胜 刘玉朋

北京工业大学机械工程与应用电子技术学院，北京，100124

自励式电磁涡流联轴器调速性能研究

梅欣鑫 叶乐志 李德胜 刘玉朋

北京工业大学机械工程与应用电子技术学院，北京，100124

针对永磁涡流联轴器调速结构复杂的问题，结合自励发电和涡流传动技术，提出一种新型自励式电磁涡流联轴器结构。通过建立自励发电和电涡流传动两部分的电磁场有限元数值模型，研究了自励式电磁涡流联轴器的发电特性和传动特性。通过对转速差、导体层和气隙长度对传动力矩影响的分析可以看出：转速差较小时，导体层选择电导率高的材料可以得到较大的力矩；铜层厚度由1 mm增大到9 mm时，传动力矩先增大后减小，在铜层厚度为5 mm时达到最大；传动力矩随气隙长度增大而减小。

涡流联轴器；自励式发电；调速特性；传动力矩

0 引言

无接触式涡流联轴器是一种利用涡流传动原理的磁力传动装置，该联轴器具有过载保护、节能环保和传动平稳等优点。涡流联轴器已广泛应用在水泵和风机等设备上，市场上常见的是永磁涡流联轴器[1-2]，永磁涡流联轴器在结构上分为盘式和筒式。盘式永磁涡流联轴器通过改变气隙长度来实现调速，而筒式永磁涡流联轴器的调速方式是改变啮合面积[3-4]。

国内外学者对永磁涡流联轴器进行了大量研究。万援[5]基于盘式永磁涡流联轴器三维有限元模型，研究了传动力矩、轴向力及效率与转速差的关系；周丽萍[6]提出一种筒式永磁涡流联轴器，并对其输出功率、传动力矩和轴向力随啮合面积和转差率的变化规律进行了深入研究。KATSUMI等[7]利用三维有限元方法研究了盘式永磁涡流联轴器产生的涡流损耗，并将估算值与实验测量值、理论计算值进行了对比。

本文针对永磁涡流联轴器调速结构复杂、永磁体高温失磁、力矩调节精度低等问题，提出一种新型自励式电磁涡流联轴器。该新型联轴器无机械运动，通过改变发电系统励磁线圈中的励磁电流大小即可实现调速，进而实现高精度力矩调节；通过电磁铁代替永磁体，解决了永磁体失磁问题；自带发电系统，满足节能的要求。

1 新型调速器结构与工作原理

如图1所示，盘式永磁涡流联轴器的结构主要是由永磁盘和导体盘构成的。永磁盘由永磁体和轭铁组成，与负载轴相连；导体盘由导体层和导磁体组成，与驱动轴相连。当驱动轴旋转时，导体盘随驱动轴以固定转速旋转，与静止的永磁盘之间产生转速差，导体层在交替变化的磁场中产生涡电流，涡电流感应的磁场又与原磁场进行耦合作用产生传动力矩，进而带动永磁盘随导体盘同向转动。通过驱动装置调节永磁盘和导体盘之间的气隙大小，改变磁场的强度，从而能实现对负载的调速。

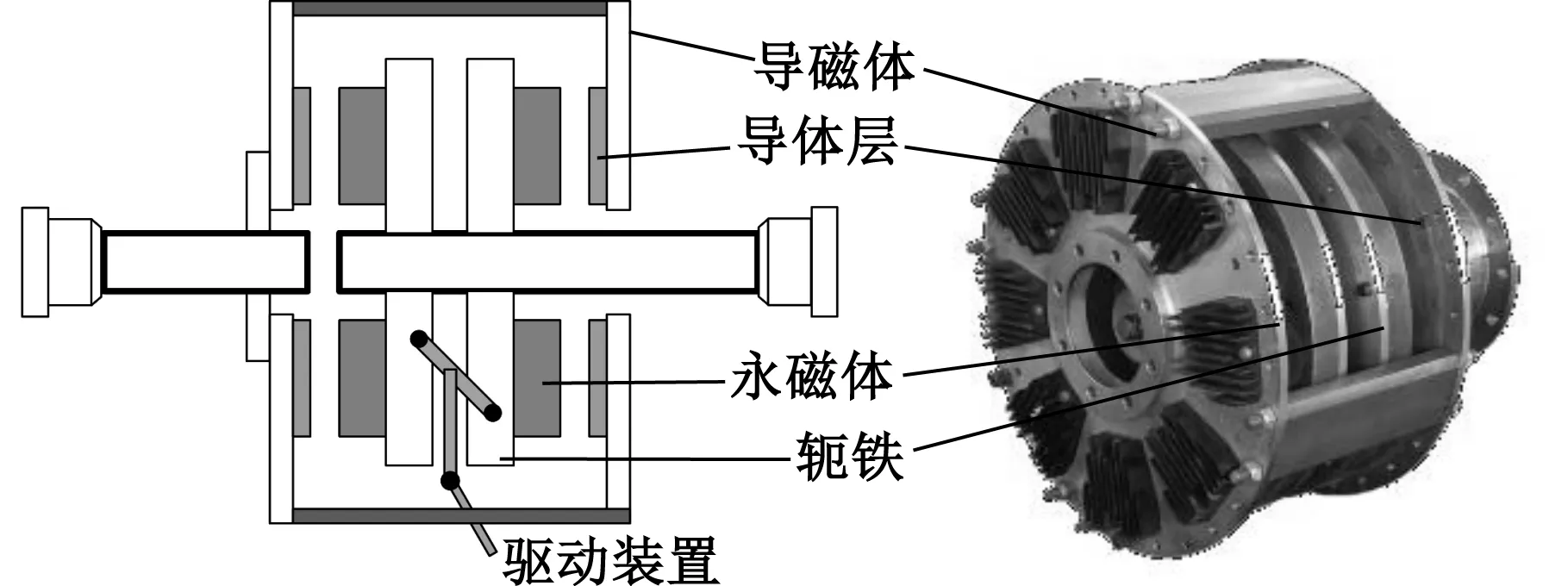
图1 永磁涡流联轴器结构示意图Fig.1 Schematic diagram of permanent magnet eddy current coupling

新型自励式电磁涡流联轴器主要由传动系统、发电系统和控制模块组成，其结构如图2所示。传动系统包括涡流线圈、电磁铁芯、铁芯保持架、导体层和导磁体，若干个涡流线圈缠绕在电磁铁芯上，电磁铁芯均匀分布在铁芯保持架上；发电系统包括发电系统电枢绕组、发电系统励磁线圈、发电系统硅钢片和发电系统励磁磁极，发电系统硅钢片固定在铁芯保持架内侧作为发电系统的转子，发电系统电枢绕组与涡流线圈相连，控制模块用于调节励磁电流的大小。工作时，通过控制模块使发电系统励磁线圈通电，旋转的电枢绕组中产生感应电动势，该电动势为涡流线圈提供电压，涡流线圈中产生电流，电磁铁芯产生磁力线，导体层切割铁芯保持架上由电磁铁芯发出的磁力线,在导体层内表面产生涡流电势，从而产生传动力矩，带动负载轴旋转。通过控制模块调节发电系统励磁线圈中电流大小可对负载调速。

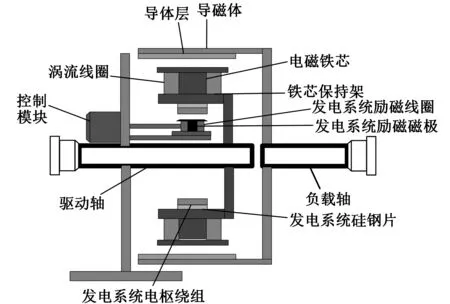
图2 自励式电磁涡流联轴器结构示意图Fig.2 Schematic diagram of self-excited electromagnetic eddy current coupling

2 联轴器设计

自励式电磁涡流联轴器设计分为传动部分和发电部分，具体包括对传动系统电磁场、传动力矩以及发电系统发电特性进行分析。

2.1传动系统设计

2.1.1磁路设计

自励式电磁涡流联轴器是以涡流线圈作为磁源的，为防止磁路达到饱和，需要对其磁路进行分析，得出气隙磁通密度的影响因素，为优化磁路提供理论依据。传动系统电磁铁芯设计成交错分布式的，为了便于分析和计算，可以将相邻两电磁铁芯的磁路等效为如图3a所示的情况。电磁铁芯发出磁力线，在铁芯、导体层、导磁体、两个气隙δ和铁芯保持架之间形成一个闭合的磁路。为了简化分析过程，对漏磁通忽略不计，可将磁路图简化为图3b所示的等效电路。

根据磁路基尔霍夫第一定律有

Φ0=Φ1+Φ1

(1)

式中，Φi(i=0，1)为各支路磁通。

对于任一闭合磁路，根据磁路基尔霍夫第二定律可知

2kNI=Φ0(R1+R2)+Φ1R1+Φ1(R0+R0)+Φ1R3

(2)

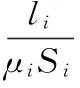
(3)

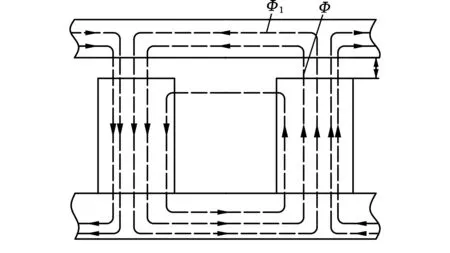
(a)磁路模型

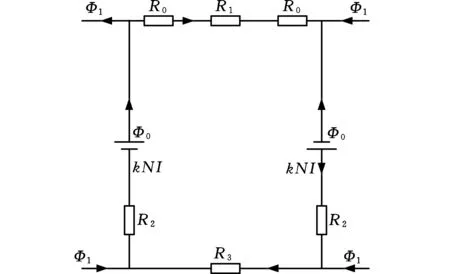
(b)等效电路图3 传动系统等效磁路模型Fig.3 Equivalent magnetic circuit model of transmission system

式中,N为涡流线圈的匝数，I为涡流线圈中的电流；μi、Si、li、Ri(i=1,2,3)分别为内转子、铁芯和外转子的磁导率、磁通面积、磁路长度以及磁阻;R0为磁路中的一个气隙磁阻。

根据式(1)～式(3)可得气隙磁通密度B0为

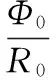
(4)

2.1.2有限元分析

为了分析联轴器传动特性，需对联轴器传动系统进行有限元仿真。图4所示为传动系统分析模型。

图4 传动系统分析模型Fig.4 The analysis model of transmission system

铁芯保持架和导磁体材料为10钢，导体层材料为铜，涡流线圈为铜线，模型主要参数如表1所示。

在分析电磁场模型时，作出以下假设：①忽略曲率和位移电流密度；②忽略磁路的迟滞损耗和杂散损耗；③忽略温升对材料特性的影响[8]。在模型仿真分析时，设定涡流线圈中励磁电流为20 A，输入转速为1500 r/min，转差率为0.05。传动系统磁通密度分布如图5所示。对磁通密度分布分析的目的是得出模型的饱和程度,避免达到设计要求之前出现饱和[9]。可以看出，最可能出现饱和的位置在由涡流线圈包围的电磁铁芯处。

表1 传动系统主要参数Tab.1 Main parameter of transmission system

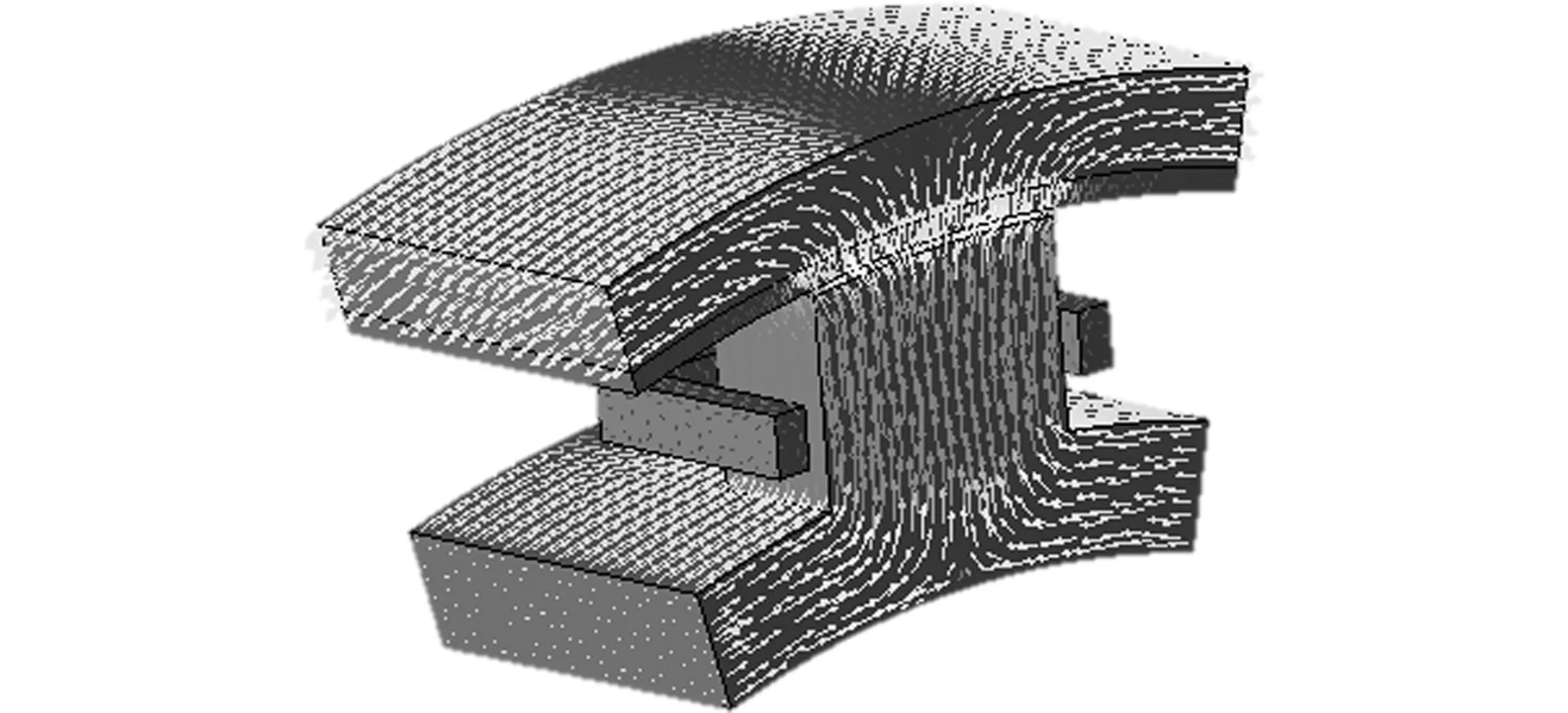
图5 传动系统磁通密度Fig.5 Magnetic flux density of transmission system

图6 传动力矩随转速差变化曲线Fig.6 Variation curve of driving torque with speed

2.2发电系统设计

2.2.1参数选型

发电系统额定数据是按传动系统的传动力矩为750 N·m时设定的，传动系统共有12个涡流线圈，采用4串3并的连接方式，总电阻为1.89 Ω，每个涡流线圈需20 A励磁电流，需要发电系统提供总励磁电流60 A,输入转速为1500 r/min，因此可以将发电系统的额定功率设为6.8 kW，整流电压为110 V。发电系统额定数据见表2。

表2 发电系统额定数据Tab.2 Rating data of power generation systems

2.2.2电磁设计与仿真分析

对发电系统部分取模型的1/12进行分析，边界条件采用反对称周期边界。图7所示为发电系统有限元分析模型。

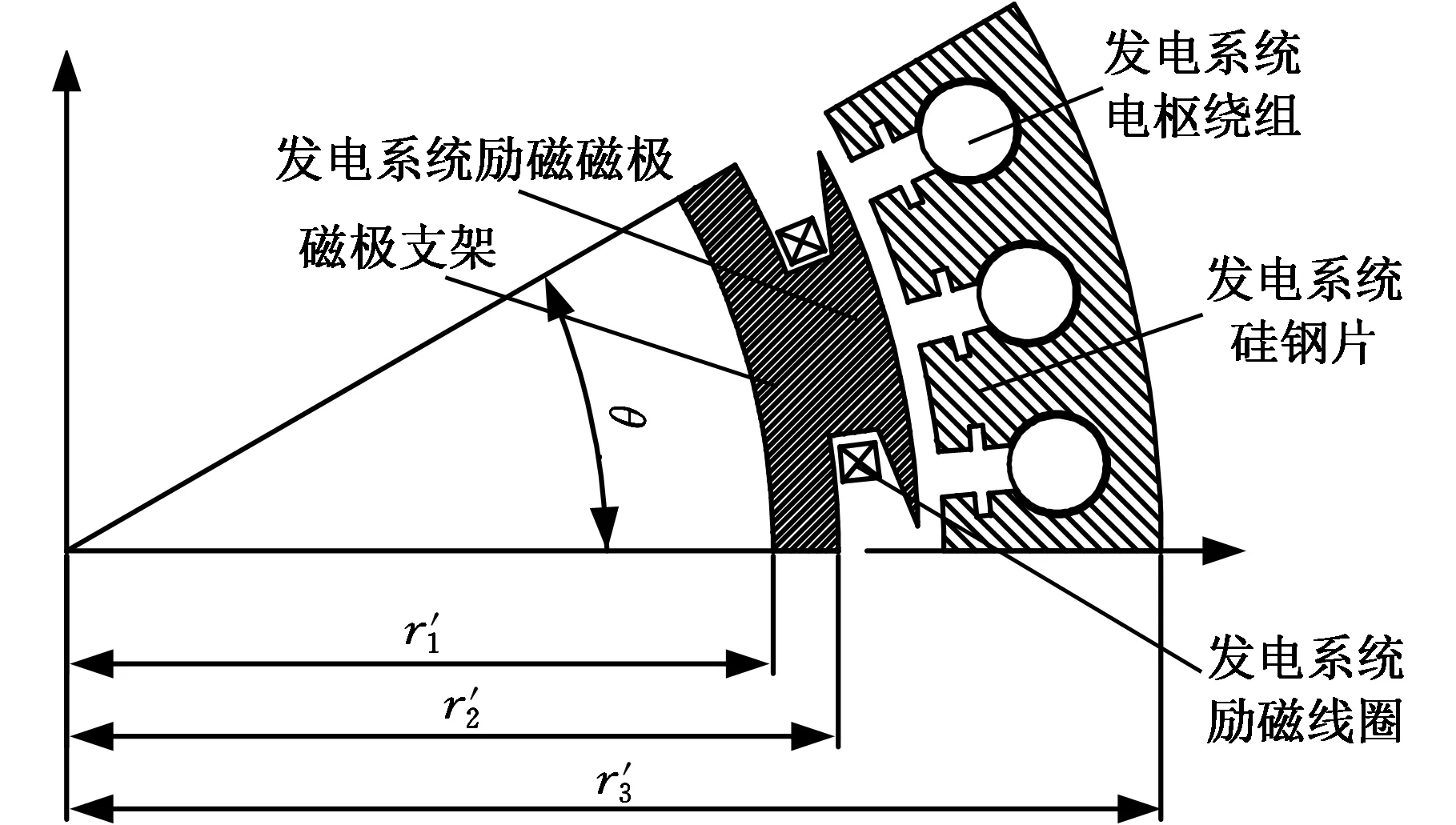
图7 发电系统有限元分析模型Fig.7 Finite element analysis model of power generation system

发电系统励磁磁极由硅钢片叠成，励磁线圈和电枢绕组均为铜线。发电系统主要参数见表3。

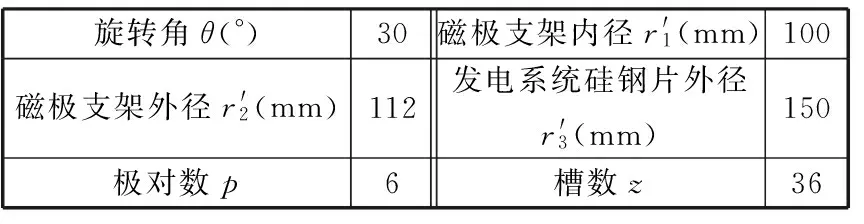
表3 发电系统主要参数Tab.3 Main parameters of power generation system

图8所示为发电系统有限元分析外部电路。由于发电系统的外部负载就是传动系统的涡流线圈，在外部电路中把负载简化为电阻值为1.89 Ω的电阻，电流表A测量负载电流Id,电压表V1、V2的差值即是负载的端电压。发电系统发出的三相交流电需要经过整流器整流成直流电后，再提供给传动系统涡流线圈。

真正走近东浒村这棵千年古樟后，我才看到了它身上的两道伤疤：一处是被“断臂”后的伤口，另一处是被剥皮后的“毁容”。

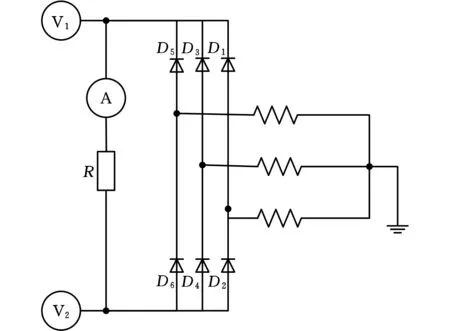
图8 发电系统有限元分析外部电路Fig.8 External circuit for finite element analysis of power generation systems

设定转速n=1500 r/min，分别对空载和负载工况进行瞬态仿真，得到发电系统磁通密度分布云图见图9，发电系统内部磁场分布均匀，无饱和现象，验证了发电系统主体设计符合工作要求。

图10给出了发电系统在转速n=1500 r/min时，空载工况下仿真得到的气隙磁通密度分布曲线，从图中可以看出气隙磁通密度分布曲线接近正弦。

(a)空载

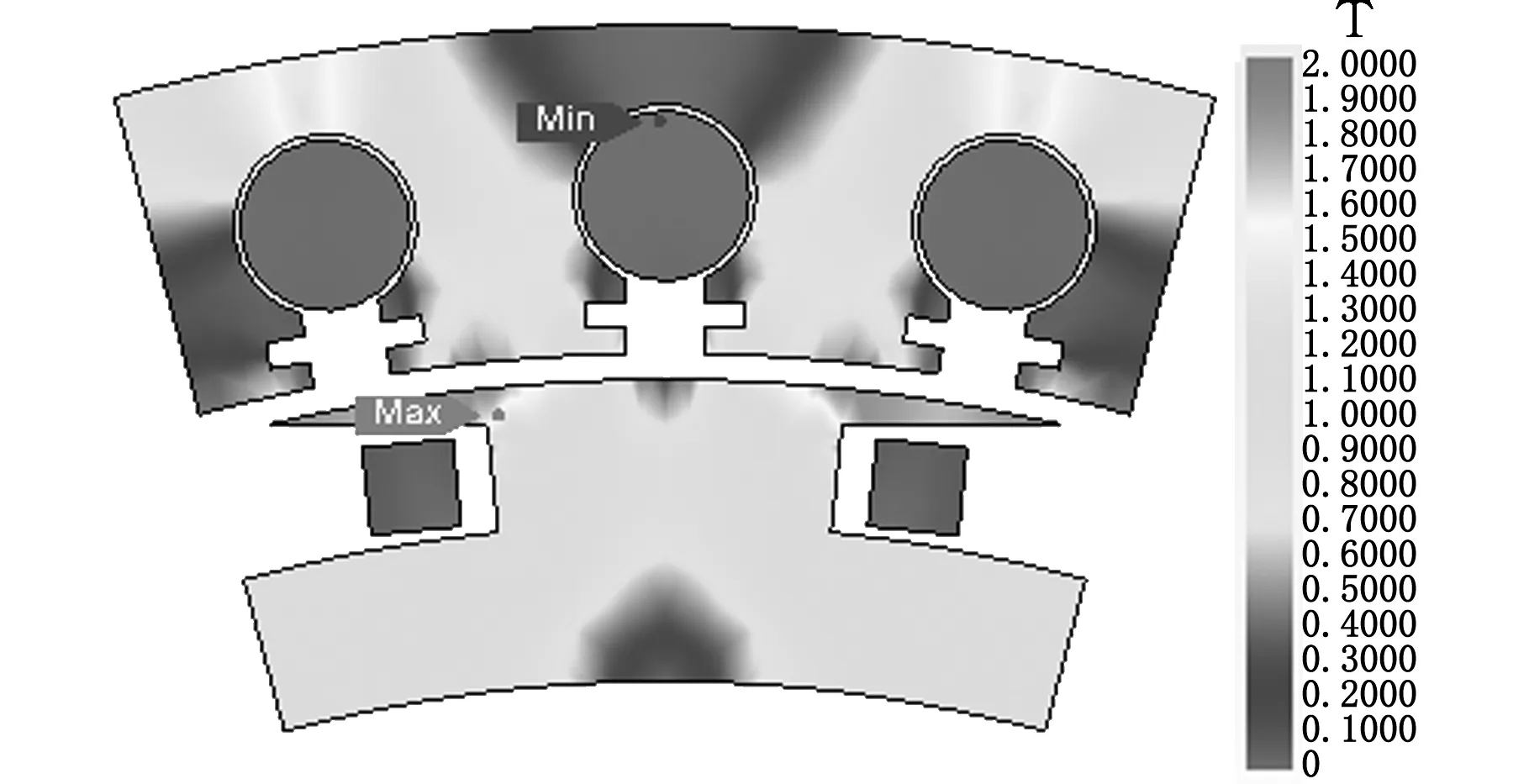
(b)负载图9 发电系统磁场分布云图Fig.9 Magnetic distribution of power generation system

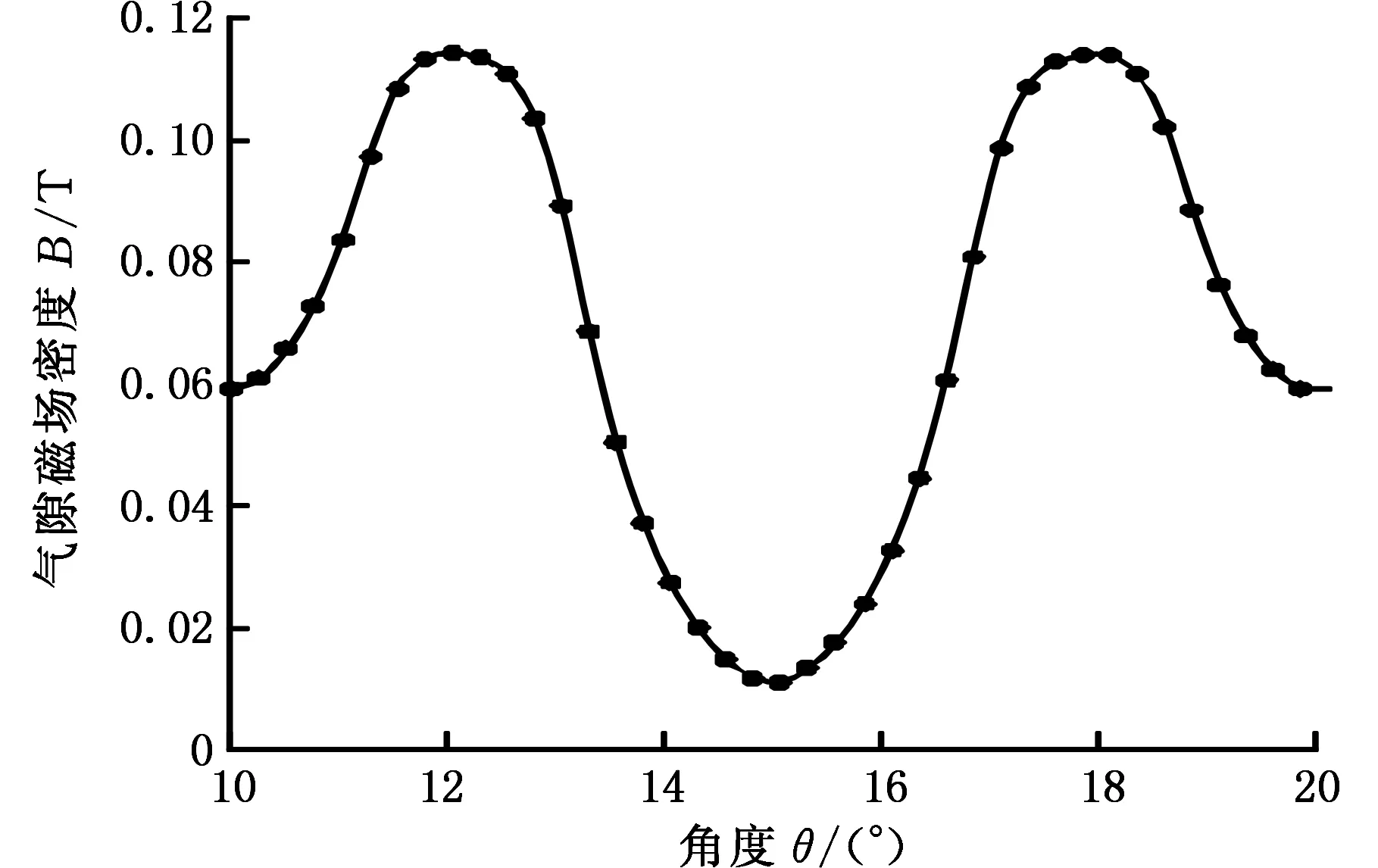
图10 发电系统气隙磁通密度分布曲线Fig.10 Air gap flux density distribution of power generation system

当转速为1000 r/min和1500 r/min时，在不同励磁电流下对发电系统进行2D瞬态场路耦合仿真，从图11中可以看出，当励磁电流大于2 A时，空载电压变化缓慢，发电系统磁路出现饱和。

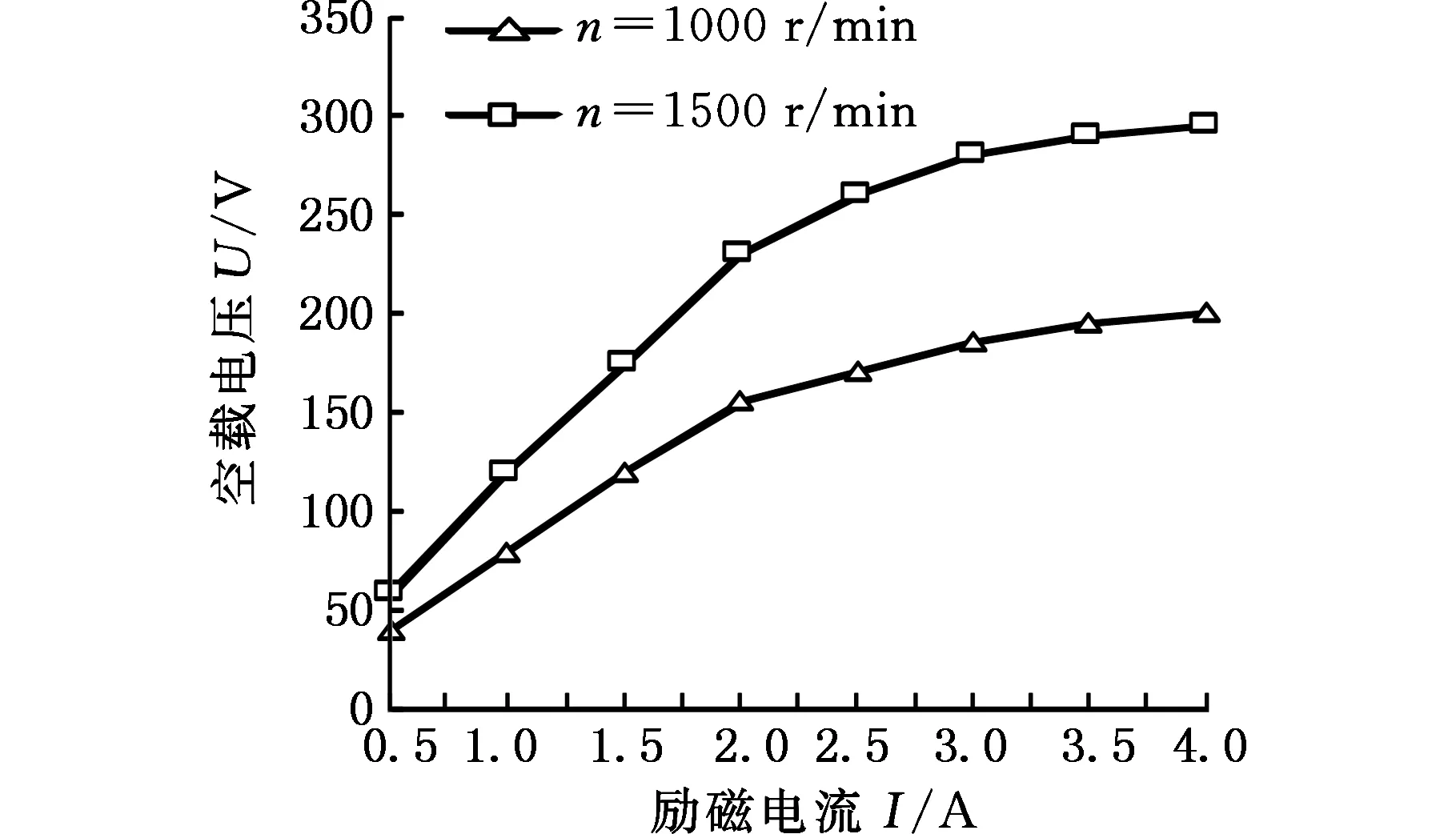
图11 发电系统空载特性曲线Fig.11 No-load characteristic curve of power generation system

在不同负载电阻RL下对发电系统进行仿真分析，对发电系统的电磁特性匹配设计有重要意义。图12为转速n=1500 r/min时拟合得到不同发电系统励磁电流下负载电阻RL与负载电流Id之间的关系曲线。

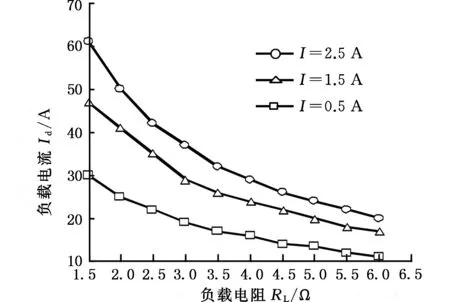
图12 1500 r/min时不同励磁电流下的RL-Id曲线Fig.12 RL-Id curves under different exciting currents at 1500 r/min

从图12可以看出，当负载电阻RL=1.89 Ω,发电系统励磁电流I=2.5 A时，负载电流Id=60 A，传动系统涡流线圈采用的是4串3并的连接方式，每个涡流线圈的励磁电流为20 A，满足传动系统的传动力矩达到750 N·m所需的励磁电流。

3 传动力矩特性分析

3.1转速差的影响

为了考察电磁涡流联轴器转速差对传动力矩大小的影响，下面分析转速差在0～300 r/min范围内传动力矩的变化情况。

转速差与传动力矩的关系见图13，当转速差在0～300 r/min变化时，传动力矩先增大后减小，这是因为导体层内表面涡流密度随着转速差增大而增大；低速时，由于涡流密度较小，涡流产生的反磁场小，磁势与磁通变化不大，传动力矩随转速差的增大而增大；当转速差进一步增大时，涡流产生的反磁场变大，总磁势与磁通减小，传动力矩减小。调速范围选在转速差为0～150 r/min时，涡流损失小，效率较高，可根据此曲线的传动力矩和转速差选择相应的电机转速。

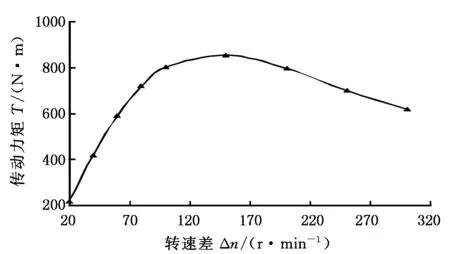
图13 传动力矩随转速差变化的关系曲线Fig.13 Relation curve of driving torque with speed

3.2导体层的影响

先考察导体层电导率的影响。保持电磁涡流联轴器工作气隙2 mm不变，分别选用不同电导率的导体层进行仿真。图14中，γ1、γ2、γ3代表导体层三种不同材料的电导率，其中γ1为铜层的电导率。图中可以看出在低转速差条件下，导体层选择电导率高的材料能得到更大的传动力矩。

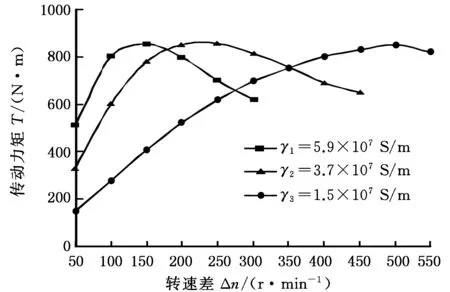
图14 不同电导率的导体层下传动力矩随转速差变化的关系曲线Fig.14 The relationship between driving torque and speed for conductor layer with different conductivities

再考察当导体层材料为铜时，铜层厚度的影响。铜层厚度从1 mm增大到9 mm，数据结果如图15所示。从图15中可以看出：转速差不变时，随着铜层厚度的增大，传动力矩先增大后减小，在铜层厚度为5 mm时达到最大值，这是因为铜的电导率较高，有利于电涡流的形成，因此传动力矩随着铜层厚度的增大而逐步变大，但是由于铜的磁导率非常低，当铜层厚度大于5 mm时，铜层表面磁场强度逐渐减小，最终导致传动力矩变小。

图15 传动力矩随铜层厚度变化的关系曲线Fig.15 The relationship between the driving torque and the thickness of copper layer

3.3气隙长度的影响

由于气隙中的磁阻要比导体中的磁阻大得多，所以磁势主要消耗在气隙中，当气隙长度增大时，气隙磁感应强度B减小，从而导致传动力矩T减小，如图16所示。

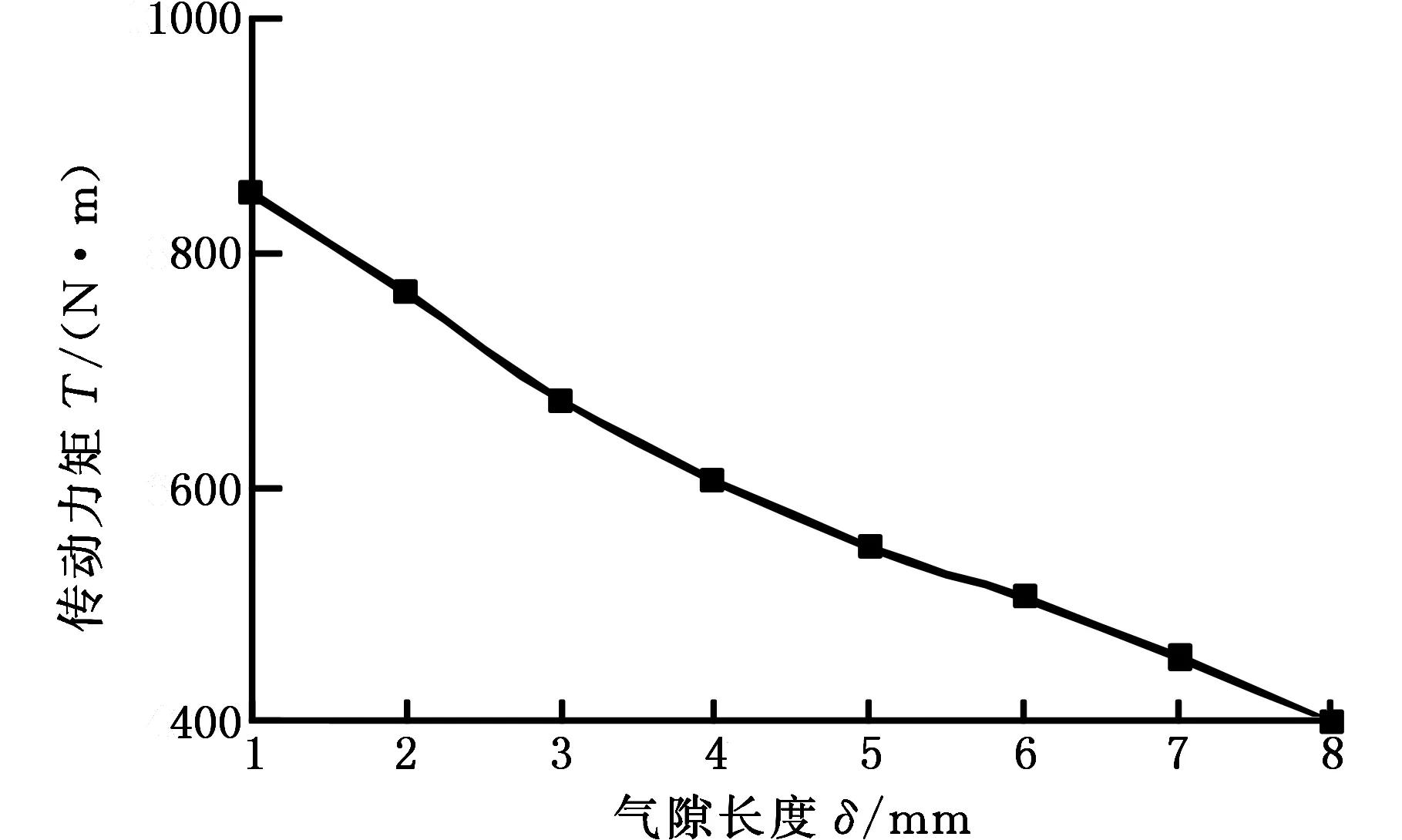
图16 传动力矩随气隙长度变化的关系曲线Fig.16 The relationship between the driving torque and the length of air gap

4 结论

(1)提出了一种新型的自励式电磁涡流联轴器，设计了发电系统和传动系统磁路结构，运用有限元法对自励式电磁涡流联轴器的发电系统和传动系统的电磁场进行了分析。

(2)建立电磁涡流联轴器电磁场模型，并应用电磁场仿真软件，对模型进行了数值模拟分析，研究了转速差、导体层和气隙长度对传动力矩的影响。

(3)转速差较小时，导体层选择电导率高的材料可以得到较大的传动力矩；传动力矩随着铜层厚度的增大先增后减，综合考虑成本和体积因素，铜层厚度一般在5 mm；气隙长度越大，气隙磁感应强度越小，传动力矩也越小。

[1] 赵克中，徐成海．磁力驱动器涡流损失的研究[J]．化工机械，2003，30(6)：326-328． ZHAO Kezhong，XU Chenghai．Study of the Eddy Current Loss of Magnetic Actuator[J]．Chemical Engineering & Machinery,2003，30(6)：326-328．

[2] 王旭，王大志，刘震，等．永磁调速器的涡流场分析与性能计算[J]．仪器仪表学报，2012，33(1)：156-160． WANG Xu，WANG Dazhi，LIU Zhen，et al．Eddy Current Field Analysis and Performance Calculations for Adjustable Permanent Magnetic Coupler[J]．Chinese Journal of Scientific Instrument,2012，33(1)：156-160．

[3] 王坚．永磁涡流传动技术基础理论研究[D]．南京：东南大学，2014． WANG Jian．Study of the Basic Theory of Permanent Magnet Eddy Current Drive Technology[D]．Nanjing：Southeast University，2014.

[4] 孙中圣，李新泉，李小宁．永磁涡流调速器研究与应用[J]．机械制造与自动化，2016(3)：1-4. SUN Zhongsheng，LI Xinquan，LI Xiaoning．Research on Permanent Magnet Adjustable Speed Driver and Its Application[J]．Machine Building and Automation，2016(3)：1-4.

[5] 万援．调速型稀土永磁磁力耦合器的性能研究 [D]．沈阳：沈阳工业大学，2013． WAN Yuan．Study on Performance of Adjustable-speed Permanent Magnet Coupling[D]．Shenyang：Shenyang University of Technology，2013．

[6] 周丽萍．新型永磁涡流调速器的特性研究 [D]．南京：南京理工大学，2015． ZHOU Liping．Characteristic Research of a New Type Permanent Magnet Coupling[D]. Nanjing：Nanjing University of Science and Technology，2015．

[7] KATSUMI Y, ATSUSHI A．Loss Analysis of Interior Permanent Magnet Motors Considering Carrier Harmonics and Magnet Eddy Currents Using 3-D FEM[J].IEEE Transactions on magnetic：2007，40(2):659-665.

[8] 叶乐志．汽车永磁缓速器设计理论与试验研究[D]．北京：北京工业大学，2012． YE Lezhi．Design Theoretical and Experimental Study on Permanent Magnet Retarder for Vehicle[D]．Beijing：Beijing University of Technology，2012．

[9] 张凯，李德胜，郑然，等．液冷自励式电磁缓速器研究[J]．农业机械学报，2014，45(11)：20-26． ZHANG Kai，LI Desheng，ZHENG Ran，et al． Study of a Self-excited and Liquid-cooled Electromagnetic Retarder [J]. Transactions of the Chinese Society of Agricultural Machinery，2014，45(11)：20-26．

(编辑王艳丽)

ResearchonSpeedRegulationPerformanceofSelf-excitedElectromagneticEddyCurrentCouplings

MEI Xinxin YE Lezhi LI Desheng LIU Yupeng

College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, Beijing，100124

Due to the complex structures of a permanent magnet eddy current coupling, this paper presented a novel structure of self-excited electromagnetic eddy current couplings, which combined the technology of excitation power generation and eddy current drive. The generating characteristics and the drive characteristics were studied on the self-excited electromagnetic eddy current couplings by establishing the finite element numerical model of the electromagnetic fields for excitation power generation and eddy current drive. The influences of rotational speed differences, conductor layers and air gap lengths on the driving torque were analyzed, then draw a conclusion that when the materials with high conductivity are used for the conductor layers, a larger torque at a low rotational speed differences may be obtained; when the thicknesses of copper layers increase from 1 mm to 9 mm, the driving torque increases first and then decreases, and the maximum of the driving torque is reached at thickness of 5 mm. The driving torque reduces along with the increments of the air gap lengths.

eddy current coupling; self-excited generator; speed regulation characteristics; driving torque

2016-11-07

北京市科技新星计划资助项目(Z151100000315079)

TH133.4

10.3969/j.issn.1004-132X.2017.17.010

梅欣鑫，男，1992年生。北京工业大学机械工程与应用电子技术学院硕士研究生。主要研究方向为电磁涡流传动。叶乐志(通信作者)，男，1982年生。北京工业大学机械工程与应用电子技术学院博士、讲师。E-mail:yelezhi@bjut.edu.cn。李德胜，男，1962年生。北京工业大学机械工程与应用电子技术学院教授、博士研究生导师。刘玉朋，男，1994年生。北京工业大学机械工程与应用电子技术学院硕士研究生。