考虑牙间均载的拉杆螺纹连接多目标优化

林谢昭 王福振

福州大学机械工程及自动化学院，福州，350108

考虑牙间均载的拉杆螺纹连接多目标优化

林谢昭 王福振

福州大学机械工程及自动化学院，福州，350108

为提高机架螺纹连接寿命，运用弹塑性接触有限元方法对拉杆连接螺纹进行强度分析，结合参数化建模，建立考虑牙间均载和应力峰值的多目标优化模型，采用径向基函数(RBF)神经网络方法和带精英策略的非支配排序遗传算法(NSGA-Ⅱ)求解。结果表明：牙侧角约为15°时，牙间轴向载荷分布不均匀率减小13.6%，等效应力峰值减小6.9%，第一主应力峰值减小11.5%。

螺纹连接；多目标优化；有限元分析；遗传算法

0 引言

预应力液压机机架通过拉杆与圆螺母将液压机的上梁、立柱和下梁连接在一起，形成一个力封闭框架。对于陶瓷砖压机等高频次工作的机架而言，变载荷、螺纹牙应力集中以及接触弹塑性变形等因素是导致啮合螺纹段牙根处产生疲劳破坏的主要原因。

根据疲劳损伤理论，螺纹牙根局部的高应力分布是导致疲劳破坏的直接原因,因此现有的研究大多都是针对降低牙根应力峰值而进行的。贾玉双[1]运用弹性接触理论结合内点惩罚函数法对牙高、螺距等参数进行优化。薄瑞峰等[2]对石油取芯钻具外管螺纹结构进行分析，研究钻杆螺纹牙数、牙型角、牙齿高和应力缓解槽等参数对螺纹强度的影响规律，实现了对牙齿高的优化。欧笛声等[3]以螺距、牙型角等参数为设计变量，对注塑机拉杆传动端梯形螺纹进行参数化建模，以最大等效应力为目标，进行了优化设计。然而，导致牙根部高应力分布除了螺纹牙型结构几何因素之外，承载牙间的轴向载荷分布不均匀性也是导致前三个螺纹牙高应力分布的一个重要因素[4]。因此，压机拉杆螺纹的优化问题涉及到多变量多目标的优化问题。

本文利用参数化建模技术，通过试验设计、弹塑性接触有限元分析和径向基函数(radial basis functions，RBF)神经网络法，建立以牙间轴向载荷分布不均匀系数、最大等效Mises应力及第一主应力为目标的多变量多目标优化模型，通过带精英策略的非支配排序遗传算法(non-dominated sorting genetic algorithms，NSGA-Ⅱ)求解，获得拉杆螺纹连接结构的优化结果，为大型压机的螺纹连接结构设计提供参考。

1 优化模型的建立

1.1设计变量的选取

以现有拉杆45°锯齿形螺纹为研究对象，基本牙型参数如图1所示。图1中，x1为螺距；x2为拉杆螺纹牙根部的过渡圆弧半径；x3为拉杆螺纹大径；x4为螺母大端外径；x5为工作边的牙侧角，原设计为0°；x6为螺母螺纹大径；x7为拉杆螺纹中径；x8为拉杆螺纹齿顶宽；x9为螺母牙高度；x10为螺纹理论高度；x11为螺纹牙型角；其余具体数据参照JB2076-84[5]。

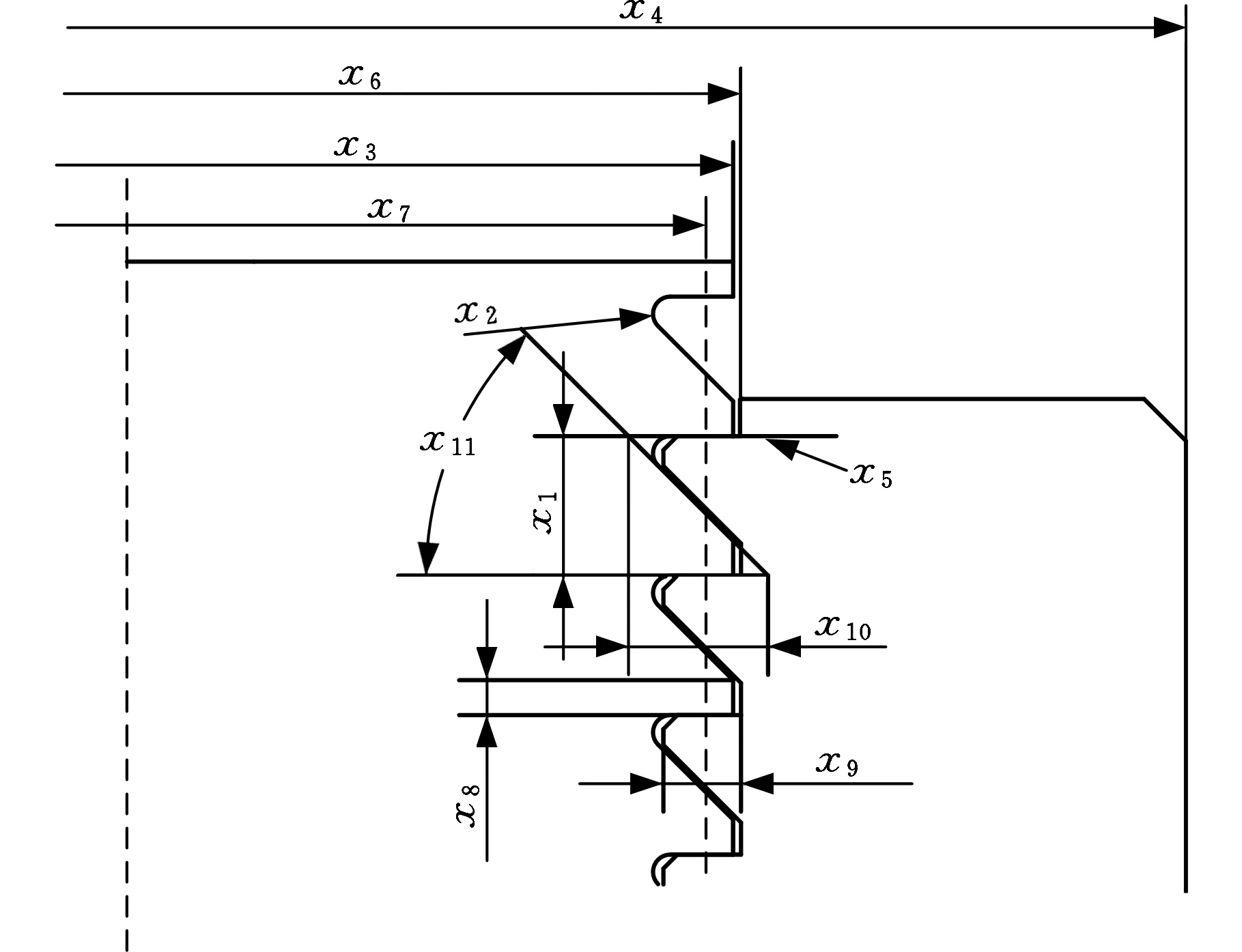
图1 45°锯齿形拉杆螺纹与螺母结构参数Fig.1 Structural parameters of 45°zigzag column thread and nut

由图1可见，拉杆螺纹连接结构的基本尺寸参数较多，考虑到螺纹参数化建模的可行性以及关键变量对拉杆连接性能的显著影响，如牙侧角的大小会影响力的传递效果，进而影响载荷的分布情况[4],螺纹连接结构承受静动载荷的能力受到螺距和拉杆螺纹外径的影响,过渡圆弧半径会直接影响应力集中大小,螺母大端外径会影响其支撑面上平均应力的大小，选取螺距x1、拉杆螺纹牙根部过渡圆弧半径x2、拉杆螺纹外径x3、螺母大端外径x4、工作边牙侧角x5五个参数作为设计变量，记为X=(x1,x2,x3,x4,x5)。

为了使模拟工况尽可能接近实际，将由机架装配体有限元分析[6]获得的拉杆截面平均拉应力转换成作用在螺母支撑面上的均布载荷，大小为279 MPa。螺母与拉杆螺纹牙之间设立接触对，设定拉杆螺纹为接触主面，螺母螺纹为接触从面，接触摩擦因数取0.12。为了提高分析的精度，对接触区域的网格进行局部细化。拉杆和螺母的材料属性如表1所示。

1.2约束条件

拉杆、螺母所受的最大应力不超过各自材料的最大许用应力，即

(1)

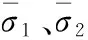
表1 拉杆和螺母材料属性Tab.1 Material properties of column and nut

1.3优化目标函数的确定

根据疲劳相关理论，疲劳裂纹是在最大切应力幅作用下萌生，而在最大主拉应力幅下扩展的[7]。由于Mises应力反映了单元体上切应力的均方根平均值，因此根据有限元计算结果，对Mises应力场和第一主应力场进行分析，有助于正确确定疲劳破坏的危险区域[7]。由于承载牙的弹性塑性变形，导致牙间载荷分布不均匀，其直接结果是导致前三个承载牙应力大，影响到拉杆螺纹的抗疲劳能力。在此，用f1=Fmax/Fmin表示螺纹牙间轴向载荷分布不均匀率，其中Fmax为最大牙载荷，Fmin为最小牙载荷。将最大Mises应力Fmises(f2)和第一主应力Fprin(f3)同时作为优化目标。

在选取设计变量参数范围时，需考虑结构不发生相互干涉，同时确保各参数的独立性及模型的整体性，参考文献[5]和设计手册中的经验范围,得到的拉杆螺纹连接优化模型为

(2)

2 多目标优化流程与分析

2.1Isight优化流程

Isight优化流程如图2所示。Isight与Abaqus的交互主要通过3个源文件：输入文件screw_rod_in.py用于编辑设计变量，建立拉杆螺纹连接结构的参数模型；screw_rod.bat文件用于调用输入文件并进行批处理；输出文件crew_rod_out.pys用于计算并输出优化目标函数值。本文采用优化拉丁超立方试验设计方法在设计空间上生成样本点，这些样本点通过调用输入文件screw_rod_in.py得到新的参数模型，由输出文件screw_rod_out.py计算出相应的响应值，然后运用径向基函数(RBF)神经网络法构建近似模型。结合NSGA-Ⅱ算法对目标函数进行寻优，得到一组Pareto最优解集。

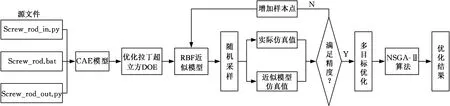
图2 Isight优化流程图Fig.2 Isight optimization flow chart

2.2径向基函数(RBF)神经网络模型及其精度检验

RBF神经网络模型是一种具有最佳逼近性能和全局最优特性的近似模型方法，并且结构简单，学习速度快，可以精确逼近复杂非线性函数。由于近似模型本身都存在一定的误差，所以本文采用复相关系数R2值检验近似模型的精度。R2值检验是指比较R2的值与1的接近程度，R2值越接近1，表示回归方程的拟合精度越高，近似效果越好。本文设计的可接受水平为0.9，表2中各目标值均达到可接受水平，说明该近似模型满足设计所需的精度。

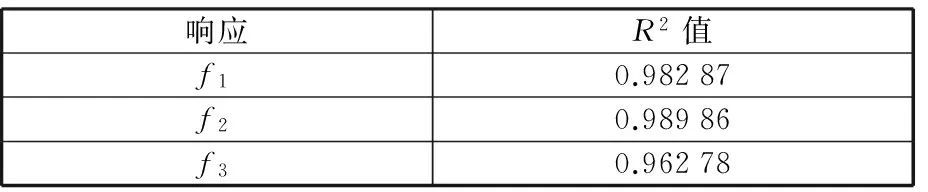
表2 R2值检验Tab.2 The value test of R2

2.3多目标优化分析

实际工程优化问题多数是多目标优化问题。要同时对多个子目标进行最优化求解，一般来说是比较困难的，甚至是根本不可能的,所以，解决多目标优化问题只能是在各个子目标之间进行协调、权衡和折中处理，使各子目标尽可能最优。多目标优化问题的解不止一个，而是一组，即Pareto解。

NSGA-Ⅱ遗传算法通过引入带精英策略的非支配排序算法,采用拥挤度和拥挤度比较算子，降低了算法的计算复杂度，使得Pareto最优解前沿中的个体能均匀地扩展到整个Pareto域，在解决拉杆螺纹结构参数优化这类多目标优化问题时表现出很大的优势[8-9]，因此本文选用NSGA-Ⅱ遗传算法进行求解。设置种群大小为40，循环代数为30，交叉概率为0.9，进行1200次迭代计算。

图3为优化后的各目标函数之间Pareto解集图。设计变量牙侧角与优化目标函数之间的关系如图4所示。

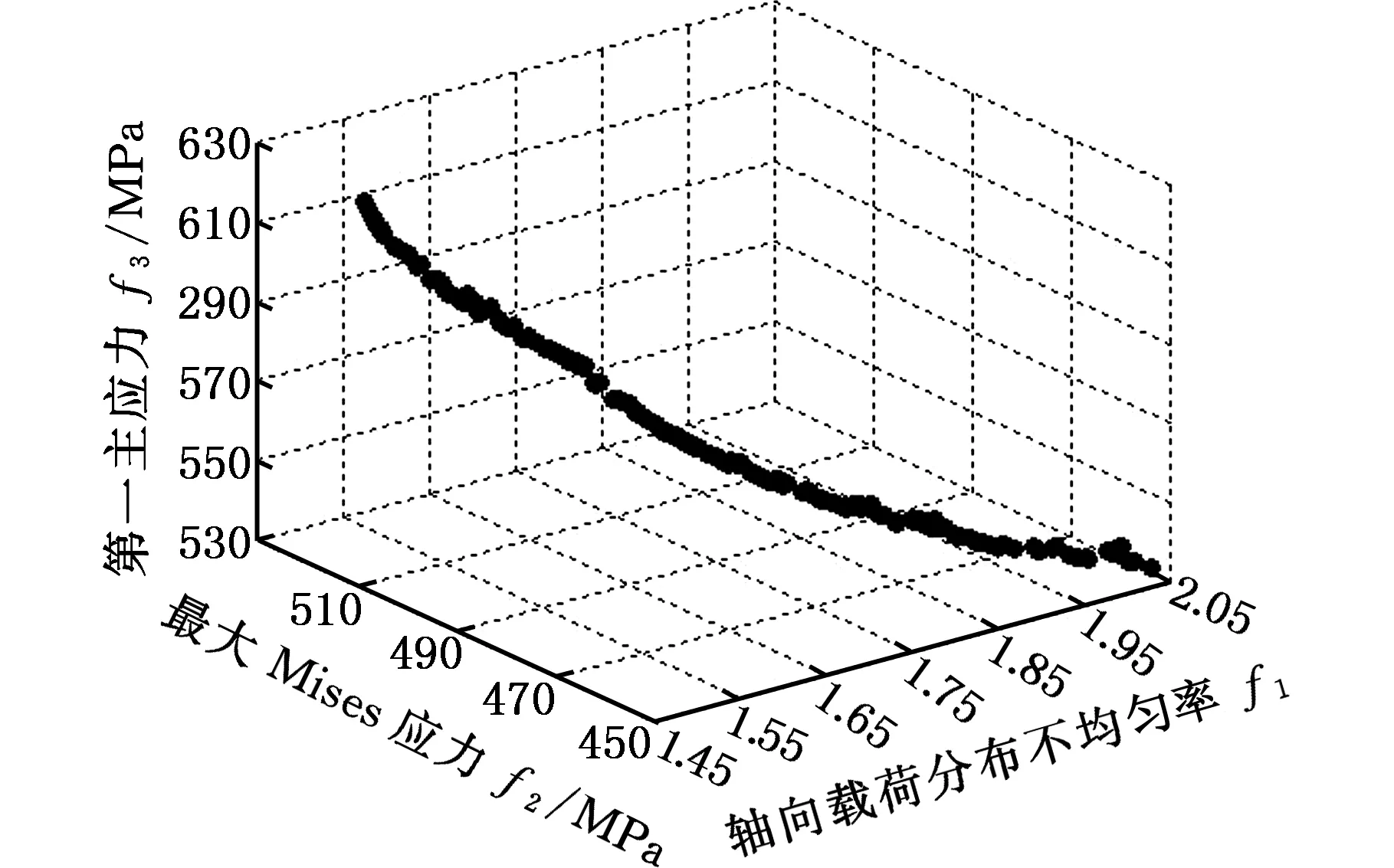
图3 优化目标三维Pareto解集图Fig. 3 3D Pareto solution set of optimizing target

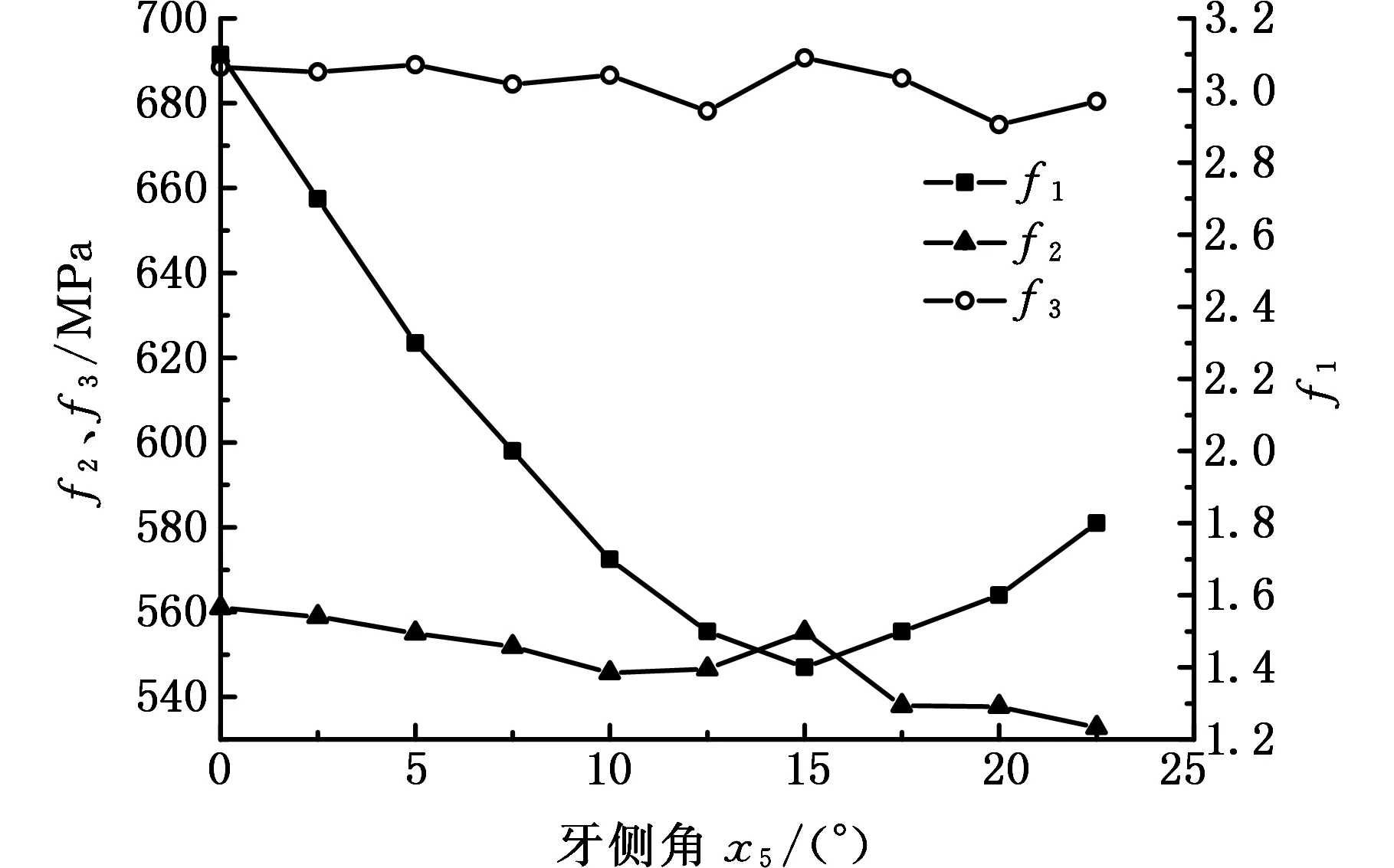
图4 牙侧角与各目标函数之间的变化趋势图Fig.4 The variation tendency of the side angle of the thread and objective function

由图4可知，随着牙侧角的增大，最大Mises应力和第一主应力上下波动，并小幅度降低，这是因为此刻螺纹牙根部发生小区域的塑性变形，牙侧角的变化对其没有显著影响。但是，牙间载荷分布不均匀率随着牙侧角增大先减小后增大，在牙侧角为15°左右时，牙间载荷分布最均匀。可以认为牙侧角为15°时有利于提高螺纹连接的疲劳寿命。

从Pareto解集中随机取出6个解的优化结果，对其数据进行圆整，并将优化结果与有限元仿真值进行对比，得到两者的相对误差值，见表3。从表3中可以看出,最大相对误差是不均匀率的相对误差,其值为3.8953%，在有限的样本点内，该误差可接受。

对Pareto解集进行分析可以发现：①螺距x1在各种优化组合下变量取值均趋于取值范围下限；②过渡圆弧半径x2和拉杆螺纹大径x3在各种优化组合下变量取值均趋于取值范围上限，说明设计螺纹连接时需尽可能增大牙根过渡圆弧半径，以降低应力集中现象；牙侧角x5和螺母大端外径x4在各优化组合下有所不同。

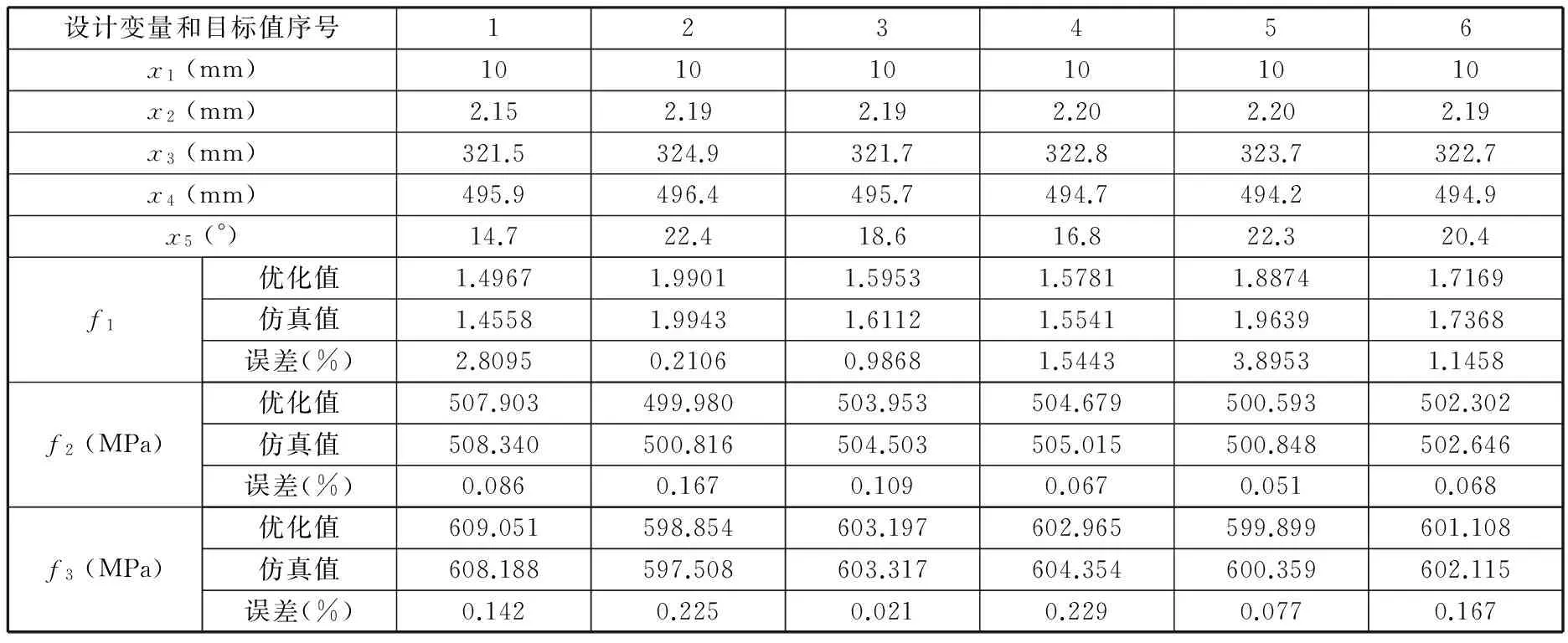
表3 优化设计结果Tab.3 Optimal design results

选取优化结果中序号1，并将其与优化前各设计变量与目标值进行对比，结果如表4所示。

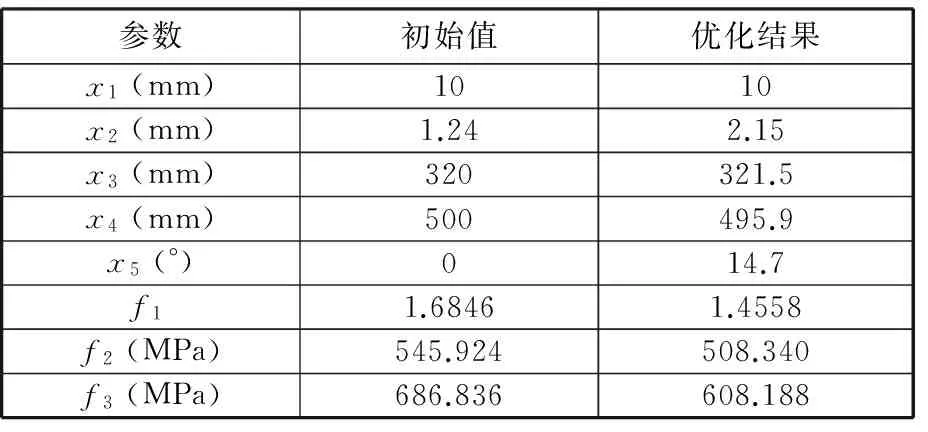
表4 优化前后各设计变量与各目标值Tab.4 Design variables and target values before andafter optimization

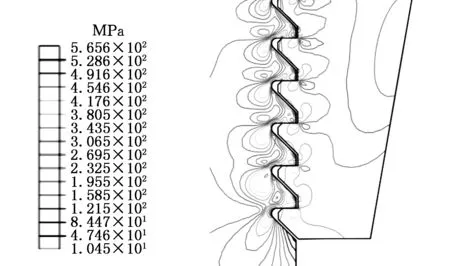
(a)优化前

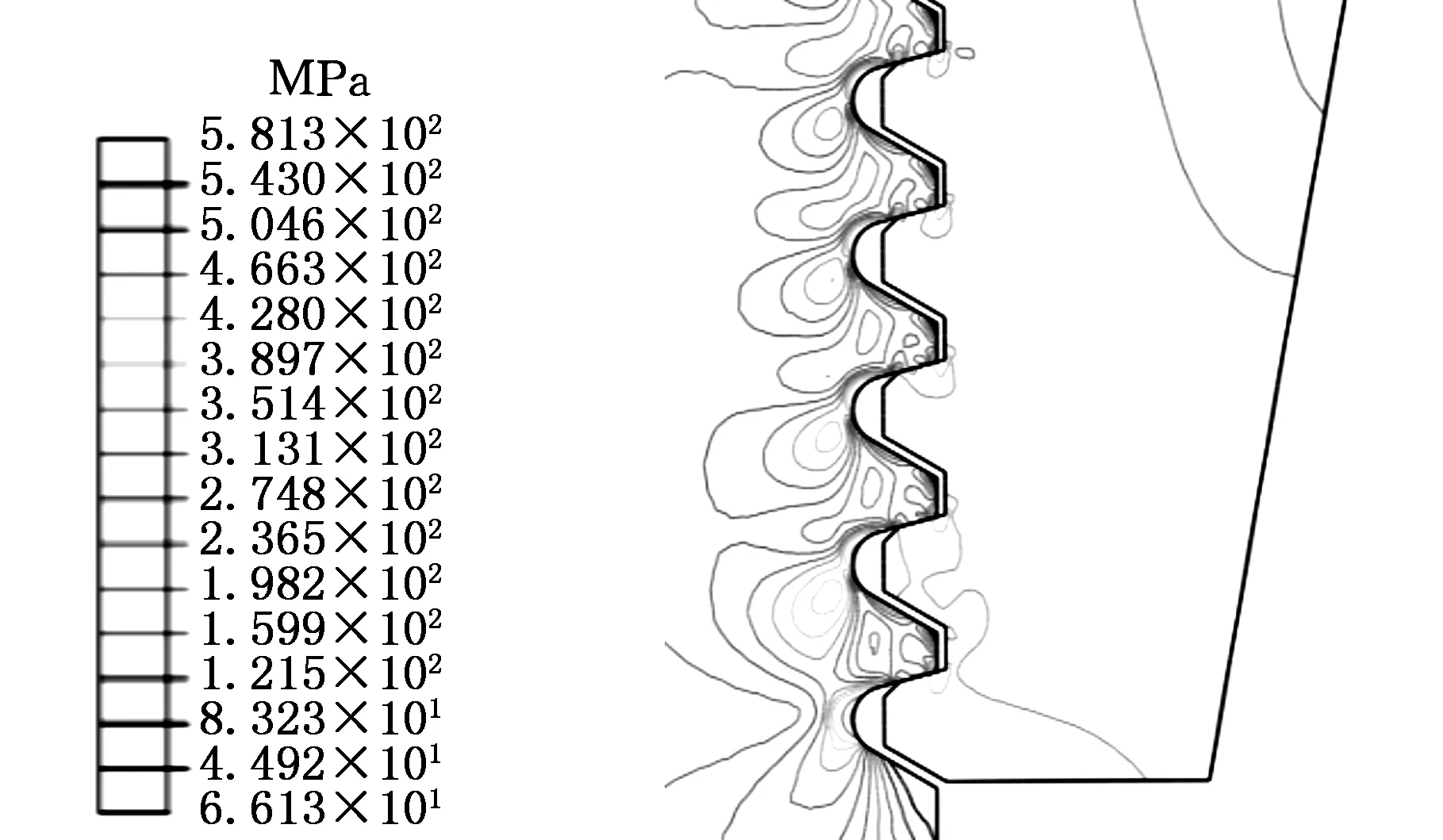
(b)优化后图5 优化前后的等效最大Mises应力分布图Fig.5 Equivalent VonMises stress distribution before and after optimization

从表4可以看出，优化后，螺纹牙的最大等效应力由原来的545.924 MPa降低为508.340 MPa，减小了6.9%，第一主应力由686.836 MPa减少到608.188 MPa，减小了11.5%，不均匀率相比优化前减小了13.6%。用ABAQUS对上述优化前后的模型分别进行计算，得到如图5、图6所示的应力分布云图。由图5可见最大等效应力发生在拉杆螺纹与螺母配合的第一个牙的根部，对比图5a、图5b可以看出，优化后在拉杆螺纹的前三个牙根部的等效应力峰值明显减小。对比图6a和图6b可以发现，优化后第一主应力只在第一个承载牙上分布较为明显。这些都从另一个方面说明了牙间载荷分布均匀性的提高有利于降低螺纹牙根部的应力分布峰值。

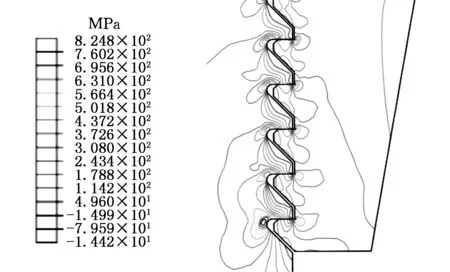
(a)优化前

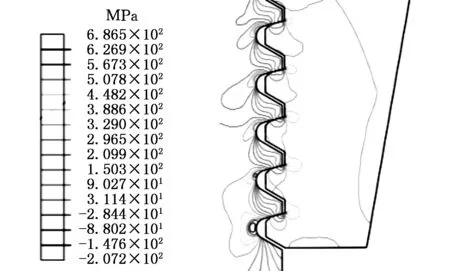
(b)优化后图6 优化前后的第一主应力分布图Fig.6 Distribution of first principal stress before and after optimization

3 结语

设计液压机预应力机架时，为了提高拉杆螺纹连接的疲劳寿命，利用Isight优化平台集成有限元分析软件ABAQUS，结合参数化技术和径向基函数神经网络方法建立了拉杆螺纹连结结构的多目标优化设计模型，选择多目标遗传算法NSGA-Ⅱ对其进行寻优，结果表明，牙侧角为15°时，牙间轴向载荷分布的均匀性最好，并且相应地降低了连结结构中Mises等效应力的峰值和第一主应力峰值，提高了拉杆螺纹连接结构的可靠性。

[1] 贾玉双. 三万吨模锻水压机立柱螺纹联结的优化设计[J]. 机械设计,2002,19(2):19-22. JIA Yushuang. Optimal Design of Column Screw-thread Connection In the 30 000-ton Hydraulic Mo-ulding Press[J]. Journal of Machine Design,2002,19(2):19-22.

[2] 薄瑞峰, 潘红军, 沈兴全, 等.石油取芯钻具外管螺纹的结构分析和参数优化[J]. 机械设计与制造,2014(9):267-269.

BO Ruifeng, PAN Hongjun, SHEN Xingquan, et al. Structural Analysis and Parameter Optimization of Outer Pipe Thread of Score Drilling Oil[J]. Machinery Design & Manufacture,2014(9):267-269.

[3] 欧笛声, 周雄新. 注塑机拉杆传动端梯形螺纹的应力分析与优化[J]. 机械设计,2007,24(6):55-57. OU Disheng, ZHOU Xiongxin. Stress Analysis and Optimization of Trapezoidal Thread at the Transmission End of a Tie-bar of the Plastic Injection Moulding Machine[J]. Journal of Machine Design,2007,24(6):55-57.

[4] 林谢昭, 林秋伟. 预应力机架连接螺纹的不同牙型力学特性分析[J]. 机械设计,2015,32(10):91-95. LIN Xiezhao, LIN Qiuwei. Research on the Mechanical Characteristics of Different Thread Forms Used in Pre-stressed Hydraulic Press Frame[J]. Journal of Machine Design,2015,32(10):91-95.

[5] 于源, 王文义. 螺纹标准大全[M]. 北京：机械工业出版社,1993:440-442. YU Yuan, WANG Wenyi. Thread Standard Book[M]. Beijing: Mechanical Industry Press,1993:440-442.

[6] 林谢昭. 液压机机架力学特性分析及轻量化设计[R]. 福州:福州大学博士后工作报告,2014. LIN Xiezhao. Mechanical Characteristics Analysis and Lightweight Design of Hydraulic Press Frame[R]. Fuzhou: Postdoctoral report of Fuzhou University,2014.

[7] 俞新陆. 液压机的设计与应用[M]. 北京:机械工业出版社,2007. YU Xinlu. Hydraulic Press Design and Application[M].Beijing: Mechanical Industry Press,2007.

[8] 尹安东, 赵韩, 杨亚娟, 等. 多目标遗传算法的混合动力传动系参数优化[J]. 中国机械工程,2013,24(4):552-556. YIN Andong, ZHAO Han, YANG Yajuan, et al. Parametric Optimization of Hybrid Powertrain Based on Multi-objective Genetic Algorithm[J]. China Mechanical Engineering,2013,24(4):552-556.

[9] 李莉. 基于遗传算法的多目标寻优策略的应用研究[D]. 无锡:江南大学,2008. LI Li. Research on Application of Multi-objective Optimization Strategy Based on Genetic Algorithm[D]. Wuxi: Jiangnan University,2008.

(编辑王艳丽)

Multi-objectiveOptimizationofThreadedConnectiononTensionRodsforaUniformLoadDistributionbetweenTeeth

LIN Xiezhao WANG Fuzhen

College of Mechanical Engineering and Automation, Fuzhou University, Fuzhou, 350108

For improving the serving life of the threaded connection, an elastic-plastic contact finite element method was used for analyzing the stress distribution of the connecting threads. After that, the parametric modeling technique was used for establishing the multi-objective optimization model where the load distribution uniform and the stress peak values were considered. This model was then solved by the radial basis function (RBF) neural network method and the elitist non-dominated sorting GA (NSGA-Ⅱ).The numerical results indicate that compare with the original design, the non-uniform rates of load distribution between the teeth in the optimized design are reduced by 13.6%, and the maximum of equivalent stresses is dropped by 6.9%, and the peak values of the first principal stress are cut down by 11.5%.

threaded connection; multi-objective optimization; finite element analysis(FEA); genetic algorithm(GA)

2016-10-31

福建省高端装备数字化设计与制造创新项目(036681)；福建省自然科学基金资助项目(2016J01227,2017J01692)

TH131.3

10.3969/j.issn.1004-132X.2017.17.002

林谢昭，男,1971年生。福州大学机械工程及自动化学院副教授、博士。主要研究方向为数字化设计。发表论文30余篇。王福振(通信作者)，男，1991年生。福州大学机械工程及自动化学院硕士研究生。E-mail:77250839@qq.com。