独立杆组参数矩阵的表达方法

卢文娟 刘若男 张立杰 张一同

1.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，0660042.燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛，066004

独立杆组参数矩阵的表达方法

卢文娟1,2刘若男1,2张立杰1,2张一同1,2

1.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，0660042.燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛，066004

并联机构中由于各杆组间的约束类型不同导致部分杆组参数向量中含有不独立的混合参数，使得对机构中输出构件自由度数目及性质、机构过约束判断的直观性变差。为构建仅含独立运动参数的杆组参数向量，分别就向量中非独立的“角运动参数”、“非衍生线运动参数”、“衍生线运动参数”展开讨论，基于螺旋理论，通过研究螺旋系的相关性，得到线性无关的基螺旋系，并等价到杆组参数矩阵中，建立独立杆组参数矩阵，最终提出参数垂直分量有效准则。结合该准则，基于GOM自由度新公式，对几种典型机构进行自由度分析，验证这些理论在独立杆组参数矩阵确定、机构自由度求解、输出构件自由度及运动性质分析、过约束判断等方面的应用。

杆组参数；混合参数；螺旋理论；衍生线运动参数

0 引言

正确分析机构自由度是机构结构设计与分析的基础和前提，自由度研究是一个已有一百六十年历史的重要课题，期间出现过几十种具有代表性的自由度公式和方法，这些方法或基于简单的代数运算[1],或基于运动方程[2-3],或基于Jacobian矩阵零空间[4]、基于群论[5-6]，亦或基于螺旋理论[7-8]、方位特征集[9]、线性变换[10]、几何代数[11]等方法。本课题组基于集合求交运算，从避开过约束角度考虑，亦于2013年提出基于杆组参数进行自由度计算的GOM(mobility of groups and output parameter)公式及相关的杆组理论[12]。

由于组成并联机构的各杆组间的约束类型可能不同(各杆组与定平台相连的运动副间布置方式可能为轴线共面、空间垂直或空间不垂直等)，在全局坐标系下不能保证每个杆组参数中均只含有独立参数，虽然用含有非独立参数的向量并不能改变机构自由度的计算结果，但会影响计算过程，使杆组对动平台的约束作用无法直接体现，一方面影响机构中过约束的判断，另一方面也无法直观地判别输出构件的自由度及性质等关键参数，所以，如何用独立参数向量来表达杆组参数矩阵，使得其中的零向量能代表杆组对动平台的真实约束，从而较为方便地判断机构中过约束、输出构件自由度及自由度性质等这些机构自由度分析中的主要结构参数，是本文讨论的重点。

1 参数垂直分量有效准则

1.1角运动参数的垂直分量有效准则

图1所示为Sarrus机构[13]，这是世界上第一个过约束机构，构成该机构的运动副全部为转动副，且包含了AC和DF两个杆组。每个杆组中的三个转动副轴线平行，称为平行R杆组。机构中两组平行R杆组中转动轴线的夹角记为φ。沿着杆组AC运动副轴线方向设为X方向，建立如图1所示坐标系。

图1 Sarrus机构Fig.1 Sarrus mechanism

(1)

其中，前三列向量分别记为RX、RY、RZ，表示X、Y、Z方向的角列向量；后三列分别记为TX、TY、TZ，表示X、Y、Z方向的线列向量。若某列向量中包含两个或两个以上零元素，则该列向量称为“多零列向量”，若该多零列向量为线列向量，称为“多零线列向量”，相对应的含有两个或两个以上零元素的角列向量称为“多零角列向量”。式(1)矩阵中Z方向的角列向量为：RZ=(0，0)T，为多零角列向量。基点参数为各杆组参数的交集：OB=(0,0,0;0,0,z)，表示动平台只能沿着Z轴方向平动，与机构真实运动相符，即此时基点参数直观地表达了输出构件的自由度及其性质。

(2)

若其中仅含独立参数向量，称为独立杆组参数矩阵，很显然这是一个混合杆组参数矩阵。基点参数为各杆组参数的交集：OB=(α,0,0;0,y,z)，表示动平台除具有沿Z方向的移动外，同时伴随有绕X轴的转动和沿Y轴方向的移动，显然这个结果与机构实际运动不相符，即对于一个混合杆组参数矩阵，其基点参数无法直接表达出输出构件的自由度及其性质。若要想用独立参数表达杆组参数矩阵，则需分析哪些参数为非独立参数。

图1所示机构中，每个杆组对输出构件均产生沿杆组运动副轴线方向的约束力(在图中用单向箭头表示)，约束力夹角为φ。当φ=90°和φ≠90°且φ≠0°时，分别得到该机构的运动螺旋系如下。

φ=90°时

(3)

φ≠90°且φ≠0°时

(4)

其中，a4、a5、a6、b4、b5、b6、d5、d6、e2、e3、e5、e6、f2、f3、f5、f6可为任意实数。经过线性变换，可以得到式(3)等价于式(4)的螺旋系，两个螺旋系的反螺旋同样相同。两种情况下，两个杆组产生两个均线性无关的约束力，约束了动平台在其平面内的移动。可理解为动平台上作用有两个共面不平行力F1和F2，其中F2可以分解为垂直于F1方向的力F2t和平行于F1方向的分力F2n，其中F2t为约束物体在平面内移动的有效分力。

结合该思想，杆组DF的运动参数同样可分解为垂直于杆组AC轴线方向，即X方向的运动参数和沿着X方向的运动参数，表示为

(5)

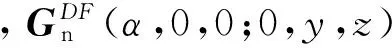
(6)

求交集得到基点参数OB=(0,0,0;0,0,z)，动平台的运动为沿Z轴方向平动。

总之，对于两组夹角不为零且共面的转动运动副，其中一组角运动参数中垂直于另一组角运动参数的分量应为有效分量，用于求解机构自由度。

1.2线运动参数的垂直分量有效准则

1.2.1移动运动副产生的线运动参数

表示移动的线运动参数一方面可由移动运动副(包括移动副)产生，称为非衍生线运动参数。另一方面可由轴线满足一定关系的多个转动运动副(包括转动副、圆柱副、螺旋副、平面副、球副、球销副)产生，称为衍生线运动参数。这里首先就非衍生线运动参数进行讨论。

(1) 当组成机构的两个杆组中的移动运动副共面但不垂直时，不考虑杆组中的其他运动，写出两个移动运动副的运动螺旋系(假设一个为沿X轴方向的移动，另一个为XY平面内的移动)如下：

(7)

式中，a、b为任意实数。

对式(7)所表示的两个螺旋作线性运算：

$2-a$1=(0,0,0;0,1,0)

(8)

该螺旋系表示沿两个相互垂直方向的移动。写出对应的独立杆组参数矩阵为

(9)

(2)当组成机构的三个杆组中的移动运动副方向呈空间分布时，不考虑杆组中的其他运动，写出三个移动运动副的运动螺旋系(假设其中一个移动沿X轴方向)如下：

(10)

式中，ai,bi,ci(i=2,3)为任意实数。

对式(10)中的三个螺旋作线性变换，令

(11)

则$1、$″2、$″3组成新的螺旋系，且与式(10)表示的螺旋系等价：

(12)

式(12)中的三个运动螺旋表示空间三个相互垂直的移动。写出对应的独立杆组参数矩阵为

(13)

总之，对于两组夹角不为零且共面的移动运动副，其中一组线运动参数中垂直于另一组线运动参数的分量应为有效分量，用于求解机构自由度。

1.2.2转动运动副产生的衍生线运动参数

如图2所示的四杆机构，可以将其看作由定平台4、动平台2以及连接两个平台的杆组C、OA所构成的并联机构。

图2 四杆机构Fig.2 Four-link mechanism

在图2所示坐标系下，可以得到杆组参数矩阵为

(14)

式(14)表示杆组OA的各运动参数之间发生了线性相关，为混合参数向量，它不能直观地表达杆组对输出构件的约束性质。

要想得到独立杆组参数矩阵表达方式，首先写出该机构的运动螺旋系：

(15)

(16)

式(16)表示OA杆组提供绕Z方向的转动及沿X方向的移动，C杆组提供Y方向的移动及Z方向的转动，对应的独立杆组参数矩阵为

(17)

可见，杆组C提供Y方向的移动，杆组OA提供XY平面内的移动，为使得各杆组参数独立，杆组OA的运动参数中取与前一杆组移动方向相垂直的分量作为有效的分量来进行自由度计算。

总之，不管是角运动参数，还是线运动参数(包含衍生和非衍生线运动参数)，当杆组中参数发生线性相关时，为使得运动参数相互独立，以便用零参数表达杆组约束，此时其中一组运动参数中垂直于另一组运动参数的分量为有效分量，用于求解机构自由度，这一准则称为参数垂直分量有效准则。

2 一组具有不同杆组约束类型的机构自由度分析

图3所示机构[14]与图4所示机构[15]均为无汇交轴线的对称并联机构，由定平台、动平台以及三个相同的杆组所组成。每个杆组的拓扑结构均为5R，其中靠近定平台的三个转动副轴线相互平行，第四个转动副与前三个转动副相互垂直，动平台上的转动副与第四个轴线相互垂直。所不同的是，图3所示机构中定平台上的三个转动副轴线不共面，而图4所示机构中定平台上的三个转动副均与定平台共面。基于GOM公式，结合参数垂直分量有效准则，对该组机构的自由度数目、自由度性质及过约束等结构参数进行分析。

(1)坐标系建立。为使杆组参数最少，尽可能多的轴线沿坐标轴方向，设杆组1中沿R11轴线方向为X方向，分别建立如图3、图4所示的坐标系。

图3 三转动3-RRRRR并联机构Fig.3 3-RRRRR three-rotational parallel mechanism

图4 两转一移3-RRRRR并联机构Fig.4 3-RRRRR 2R1T parallel mechanism

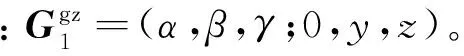
(18)

(19)

(3)计算各杆组自由度。两个机构中各杆组自由度[12]均相同：

(20)

(4)不考虑转动是否被约束，通过直接求交集得到图3机构基点参数

(21)

图4机构基点参数：

(22)

(5)基点参数有效性判别[17]。由于矩阵M1中不含多零线列向量，转动不受约束，则

(23)

式中，dB1为机构的基点参数的阶。

矩阵M2中含Y方向的多零线列向量：TY=(y,0,0)T，杆组2和杆组3在Y方向产生了平行约束力，约束一个方向的转动，使得基点参数中的γ成为无效参数：

(24)

(6)机构自由度计算。根据GOM公式，得图3机构自由度[12]：

(25)

图4机构自由度：

(26)

(7)自由度性质判别。各机构杆组参数矩阵中仅含有独立参数，则对应的基点参数OB1和OB2表示机构动平台的运动：图3所示机构具有三个转动自由度；图4机构具有两个转动和一个移动自由度。

(8)过约束判别[18]。由于杆组参数矩阵中不含混合参数，其中的零参数真实地反映了各杆组对动平台的约束作用，根据其中的多零列向量，结合过约束的特征及判断准则，可对机构中的过约束进行判别。图3机构对应的杆组参数矩阵M1中，如式(18)所示，不含多零列向量，机构中不含过约束。图4对应的杆组参数矩阵M2中，如式(19)所示，含有Y方向的多零线列向量TY=(y,0,0)T，两个Y方向的约束力共面，且约束了Z方向的转动，构成实际约束，机构中亦无过约束。

需要说明的是，传统的这类机构多为杆组中含有球面副或者含有多个空间汇交于一点的转动副，给实际的加工和制造带来很大困难，难以保证精度，上述这类无汇交轴线的对称并联机构的提出为方便机构的加工和精度的提高提供了途径。

3 含有过约束的五杆铰链双滑块机构自由度分析

图5所示为一个五杆铰链双滑块机构。在几何条件上机构保持OA=AB=AC及相互垂直的两个滑道。该机构是典型的平面过约束机构，也是平面机构自由度分析中的一个难点。学者们也曾用多种不同的方法，包括经验法、螺旋理论[8]、速度瞬心法[19]、运动副约束特性分析法[20]、拆分杆组法[21]等对其自由度进行分析，这里我们尝试用GOM公式对其自由度及过约束进行求解。

图5 五杆铰链双滑块机构Fig.5 Five-link two-slider mechanism

(1)坐标系建立。该平面机构可看作由定平台5，动平台2以及连接这两个平台的杆组B、杆组OA、杆组C组成的并联机构。为使杆组参数最少，尽可能多的轴线沿坐标轴方向，设杆组B中沿移动副轴线方向为X方向，杆组C中沿移动副轴线方向设为Y方向，建立如图5所示的坐标系。

(2)确定独立杆组参数矩阵。杆组B中包含Z方向一个转动副和X方向一个移动副，产生一个角运动参数γ和一个线运动参数x，得到其杆组参数向量为

杆组OA中含有两个轴线平行的转动副，产生一个角运动参数γ和两个衍生线运动参数x和y，但是此时三个参数线性相关，为使得各参数相互独立，根据1.2.2节中转动运动副产生的衍生线运动参数的垂直分量有效准则，杆组OA的运动参数中取与B杆组移动方向相垂直的分量作为有效分量来进行自由度计算，得到对应的独立参数向量为

杆组C的杆组参数向量与杆组B类似，为

于是该机构的独立杆组参数矩阵为

(27)

(3)计算各杆组自由度。各杆组自由度[12]均相同：

(28)

(4)不考虑转动是否被约束，通过直接求交集得到基点参数

(29)

(5)基点参数有效性判别[17]。矩阵M中含X方向的多零线列向量：TX=(x，0，0)T，杆组OA和杆组C在X方向产生了平行约束力，而该两个约束力作用线均通过D点，构成共线的约束力：

(30)

(6)机构自由度计算。基于GOM公式得[12]

(31)

(7)自由度性质判别。各杆组参数中均只含独立参数，则基点参数表示机构动平台的运动：XY平面内的一个转动。

(8)过约束判别[18]。杆组参数矩阵M中，X和Y方向存在一个全为零的角列向量，RX=(0,0,0)T，RY=(0,0,0)T，RX、RY表示图5所示机构中存在两个公共约束，为X和Y方向的约束力偶。Z方向存在一个全为零的线列向量TZ=(0,0,0)T，TZ表示动平台上作用有三个平行的Z方向约束力，且三个约束力作用线均通过D点，即三个作用力共轴，构成一个公共过约束，该过约束为Z方向的约束力。式(2)所示矩阵M中同样含有X方向的多零线列向量：TX=(x,0,0)T，该向量表示动平台上作用有两个X方向的平行约束力，且两个约束力作用线均通过D点，这两个共轴的约束力构成一个局部过约束。

于是，该机构中含有三个公共过约束，机构的阶为3，同时含有一个局部过约束，与其他方法分析的结果完全一致。

4 结论

(1)杆组参数矩阵的确定是正确应用GOM公式进行机构自由度分析的前提，本文就如何解决杆组参数矩阵中参数独立性的问题展开讨论，所研究内容是对基于杆组参数进行自由度求解方法的补充和完善。

(2)在定义独立运动参数、混合运动参数、独立参数向量、混合参数向量、独立杆组参数矩阵、衍生线运动参数、非衍生线运动参数等概念的基础上，基于螺旋理论，分别分析了杆组参数中角运动参数、线运动参数线性相关的情况，提出了参数垂直分量有效准则：将含有混合参数的杆组运动参数中垂直于另一组运动参数的分量作为有效分量，得到独立杆组参数矩阵，用于求解机构自由度。

(3)仅含独立参数的杆组参数向量，能够较直观地表达杆组对动平台的约束作用，从而方便确定机构中过约束、输出构件的自由度及性质等这些自由度分析中的主要结构参数。

[1] CHEBYCHEV P A. Théorie des Mécanismes Connus Sous le nom de Parallélogrammes, 2ème Partie[J]. Mémoires présentés àl Académie impériale des sciences de Saint-Pétersbourg par divers savants,1869:2.

[2] WALDRON K J. The Constraint Analysis of Mechanisms[J]. Journal of Mechanisms,1966,1:101-114.

[3] DAVIES T H. Mechanical Networks—1. Passivity and Redundancy[J]. Mechanism and Machine Theory,1983,18(2):95-112.

[4] ANGELES J, GOSSELIN C. DÉTermination du Degré de Liberté des Chanes Cinématiques Simples et Complexes[C]// 7th IFToMM World Congress on the Theory of Machines and Mechanisms. Seville, Spain.1987:199-202.

[5] HERVÉ J M. Analyse Structurelle des Mécanismes par Groupe des Déplacements[J]. Mechanism and Machine Theory,1978,13(4):437-450.

[6] RICO J M, AGUILERA L D, GALLARDO J, et al. A More General Mobility Criterion for Parallel Manipulators[J]. ASME Journal of Mechanical Design,2006,128(1):207-219.

[7] TSAI L W. Robot Analysis: the Mechanics of Serial and Parallel Manipulators[M]. New York: Wiley-Interscience,1999.

[8] 黄真, 刘婧芳, 李艳文. 论机构自由度——寻找了150年的自由度通用公式[M]. 北京: 科学出版社,2011. HUANG Zhen, LIU Jingfang, LI Yanwen. On the Degree of Freedom—The General Formula of the Degree of Freedom Which Has Been Searched for 150 Years[M]. Beijing: Science Press,2011.

[9] 杨廷力, 刘安心, 罗玉峰, 等. 机器人机构拓扑结构设计[M]. 北京: 科学出版社,2012. YANG Tingli, LIU Anxin, LUO Yufeng, et al. Theory and Application of Robot Mechanism Topology[M]. Beijing: Science Press,2012.

[10] GOGU G. Mobility and Spatiality of Parallel Robots Revisited via Theory of Linear Transformations[J]. European Journal of Mechanics A/Solids,2005,24(4):690-711.

[11] LI Qinchuan, CHAI Xinxue, XIANG Ji’nan. Mobility Analysis of Limited-DOF Parallel Mechanisms in the Framework of Geometric Algebra[J]. ASME Journal of Mechanisms and Robotics,2016,8(4):041005-1-9.

[12] ZHANG Yitong, LU Wenjuan, MU Dejun, et al. Novel Mobility Formula for Parallel Mechanisms Expressed with Mobility of General Link-group[J]. Chinese Journal of Mechanical Engineering,2013,26(6):1082-1090.

[13] SARRUS P F. Note Sur la Transformation does Mouvements Rectilignes Alternatifs En Mouvements Circulaires Et Reciproquement. Academie des Science[J].CR Hebd. Sci., Paris,1853,36:1036-1038.

[14] CHEN Ziming, CAO Wen’ao, HUANG Zhen. Type Synthesis of 3-DOF Rotational Parallel Mechanisms with No Intersecting Axes[C]//ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Chicago, IL, USA,2012:565-572.

[15] 丁华峰, 曹文熬, 陈子明, 等. 无汇交轴线的对称两转动一移动并联机构：201210076891.X.[P].2012-08-08. DING Huafeng, CAO Wen’ao, CHEN Ziming, et al. A 2-DOF Rotational and 1-DOF Translational Symmetrical Parallel Mechanism without Intersecting Axes：201210076891.X[P].2012-08-08.

[16] 卢文娟, 张立杰, 曾达幸, 等. 新的机构自由度计算公式——GOM公式的应用研究[J]. 中国机械工程,2014,25(17):2283-2289. LU Wenjuan, ZHANG Lijie, ZENG Daxing,et al. Research on Application of GOM Formula—a Novel Mobility Formula[J]. China Mechanical Engineering,2014,25(17):2283-2289.

[17] 卢文娟, 张立杰, 张一同. 基于交集运算的自由度快速求解方法[J]. 中国机械工程,2015,26(4):522-528. LU Wenjuan, ZHANG Lijie, ZHANG Yitong. Fast Solution Method of Mobility Calculation based on List Intersection[J]. China Mechanical Engineering,2015,26(4):522-528.

[18] 卢文娟, 张立杰, 曾达幸, 等. 基于一种自由度新理论的过约束判断方法[J]. 机械工程学报,2014,50(13):59-66. LU Wenjuan, ZHANG Lijie, ZENG Daxing,et al. A Method for Determination of Overconstraint based on a New Mobility Theory[J]. Journal of Mechanical Engineering,2014,50(13):59-66.

[19] 佟士懋. 探讨利用速度瞬心法鉴别平面机构的虚约束[J]. 北京联合大学学报,2011,25(1):41-45. TONG Shimao. Indentification of Redundant Constraints in a Planar Mechanism Using Either the Graph of Instantaneous Centers or the Property of the Graph’s Adjacency Matrix[J]. Journal of Beijing Union University,2011,25(1):41-45.

[20] 郭卫东, 于靖军. 一种计算平面机构自由度的新方法[J]. 机械工程学报, 2013, 49(7): 125-129. GUO Weidong, YU Jingjun. A New Method of Mobility Calculation for Planar Mechanisms[J]. Journal of Mechanical Engineering,2013,49(7):125-129.

[21] 黄真, 曾达幸. 机构自由度计算原理和方法[M]. 北京: 高等教育出版社,2016. HUANG Zhen, ZENG Daxing. Mobility Principles and Methods for Mechanisms[M]. Beijing: Higher Education Press,2016.

(编辑王艳丽)

ExpressingMethodforanIndependentLinkGroupParameterMatrix

LU Wenjuan1,2LIU Ruonan1,2ZHANG Lijie1,2ZHANG Yitong1,2

1.Parallel Robot and Mechatronic System of Laboratory of Hebei Province, Yanshan University, Qinhuangdao,Hebei,066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science, Ministry of Education,Yanshan University, Qinhuangdao,Hebei,066004

The different types of constraints among the link groups in parallel mechanisms led to the independent and mixed parameters in part of link group parameter vectors, which made the number and engendered nature of DOFs(degree of freedoms) of output components along with the intuitiveness of judging overconstraints in the mechanisms worse. To construct the parameter vectors which only included independent motion parameters, dependent parameters in vectors such as “angular motion parameters”, “non-derivative line motion parameters” and “derivative line motion parameters” were discussed. Meanwhile based on the screw theory, the relevance of screw system was deduced to obtain the linear independent basic screw system which was equivalent into the matrix of link group parameters. Independent matrix of link group parameters was constructed. Furthermore the rule named “the validity of vertical component” was proposed. Finally based on a new mobility formula—GOM, combined with the rules mentioned above, the DOFs of several kinds of typical mechanisms were analysed. The applications of the theories presented before and herein were verified in the following parts: determination of independent matrix for link group parameters, calculations of the mobility and mobility property of output components, and determination of overconstraints.

link group parameter; mixed parameter; screw theory; derivative line motion parameter

2016-11-15

国家自然科学基金资助项目(51275438,51775473)；河北省高等学校科学技术研究项目(QN2014175)；河北省教育厅高等学校科技计划青年基金资助项目(QN2017144)

TH112

10.3969/j.issn.1004-132X.2017.17.001

卢文娟，女，1983年生。燕山大学机械工程学院副教授、博士。主要研究方向为并联机构自由度分析、型综合。发表论文10余篇。E-mail: luwenjuan@ysu.edu.cn。刘若男，女，1994年生。燕山大学机械工程学院硕士研究生。张立杰(通信作者)，男，1969年生。燕山大学机械工程学院教授、博士研究生导师。张一同，男，1945年生。燕山大学机械工程学院教授。