考虑产品性能偏差约束的公差优化设计

郭迎福 罗炎旺 赵延明 何鸿曦 谭华江

1.湖南科技大学机械设备健康维护湖南省重点实验室，湘潭,4112012.湖南科技大学信息与电气工程学院，湘潭,411201

考虑产品性能偏差约束的公差优化设计

郭迎福1罗炎旺1赵延明2何鸿曦1谭华江1

1.湖南科技大学机械设备健康维护湖南省重点实验室，湘潭,4112012.湖南科技大学信息与电气工程学院，湘潭,411201

实际生产过程中，影响加工成本的因素很多，很难用一个统一的数学模型来精确描述所有类型的加工成本-公差关系。以产品加工成本与质量损失成本之和最小为优化目标，以产品性能偏差与经济加工精度为约束，建立了产品的公差优化模型；然后采用遗传算法对优化模型进行求解；最后以某型号汽车空调压缩机为例验证该模型的有效性。

公差成本；性能偏差；遗传算法；公差优化

0 引言

公差优化设计对机械产品的质量影响非常大，通过公差优化设计来提高产品的质量并减少成本投入一直是国内外研究的热点。而如何建立一个合理的公差优化模型是产品公差优化设计的重点[1]。国内外学者对公差优化设计进行了深入研究，但他们的研究工作大都是基于尺寸链或传动链[2-4]。考虑产品性能稳定性的公差优化比基于尺寸链或传动链的公差优化更符合长远利益[5]，公差优化的目的就是降低公差总成本。

1 建立公差优化模型

1.1加工公差成本

在实际生产过程中，由于产品零件的形状、几何尺寸各不相同，而且影响加工成本的因素很多，很难用一个统一的数学模型来精确描述所有类型的加工成本-公差关系。国内外学者对加工成本-公差关系的数学模型做了很多研究，提出了很多可用的加工成本-公差关系数学模型。现阶段比较成熟的加工成本-公差模型有指数模型、幂指数模型、负平方模型、多项式模型和复合模型等。

零件的几何形状多种多样, 按其加工特征可分为四类, 即外圆特征、孔特征、定位特征和平面特征。这四种公差加工成本函数如下[6]：

外圆特征的尺寸公差成本函数为

(1)

式中，Ti为符合公差成本函数的任何公差T。

内孔特征的尺寸公差成本函数为

(2)

定位特征的尺寸公差成本函数为

(3)

平面特征的尺寸公差成本函数为

(4)

则关键零部件总加工成本为

(5)

1.2田口质量损失成本[7]

设产品质量特性为y，目标值为m，相应损失为L(y)，则有

L(y)=K(y-m)2

(6)

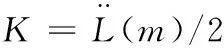
式中，K为不依赖于y的比例常数。

我们称式(6)为望目特性的质量损失函数[8]。

在公差设计中，公差为双向对称分布,即有y-m=T/2，则

(7)

式中，A为产品为不合格品时所造成的损失。

尺寸公差Ti造成的质量损失成本为[9]

(8)

关键零部件公差总的质量损失成本为

(9)

则公差总成本可表示为

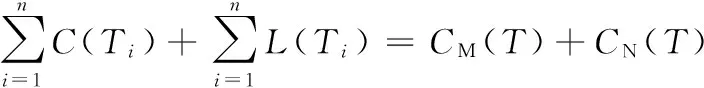
(10)

1.3约束条件

1.3.1经济加工精度约束

在进行公差优化设计时，设计的公差不能超过企业的经济加工能力范围，即

Tmini≤Ti≤Tmaxi

(11)

式中，Tmini为第i个尺寸的最小加工能力公差；Tmaxi为第i个尺寸的最大加工能力公差。

1.3.2性能偏差约束

运用多元函数的全微分理论可近似得到函数的系统误差[10]

(12)

式中，f为性能函数；Δx1,Δx2,…,Δxn为各尺寸偏差。

那么在某已知工况下，产品的性能偏差关于产品的关键零部件尺寸偏差Δx1,Δx2,…,Δxi,…,Δxn的系统误差为

(13)

ΔQmin≤ΔQ0≤ΔQmax

(14)

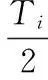
(15)

式(13)即为公差优化设计中关于尺寸偏差与性能偏差的约束方程。

1.4优化模型

综上所述，可以建立最小公差总成本优化模型如下:

1.5优化算法

在本文的公差优化模型中，目标函数与性能约束均为较复杂的非线性方程，故采用遗传算法求解是非常合适的，遗传算法的步骤见图1。

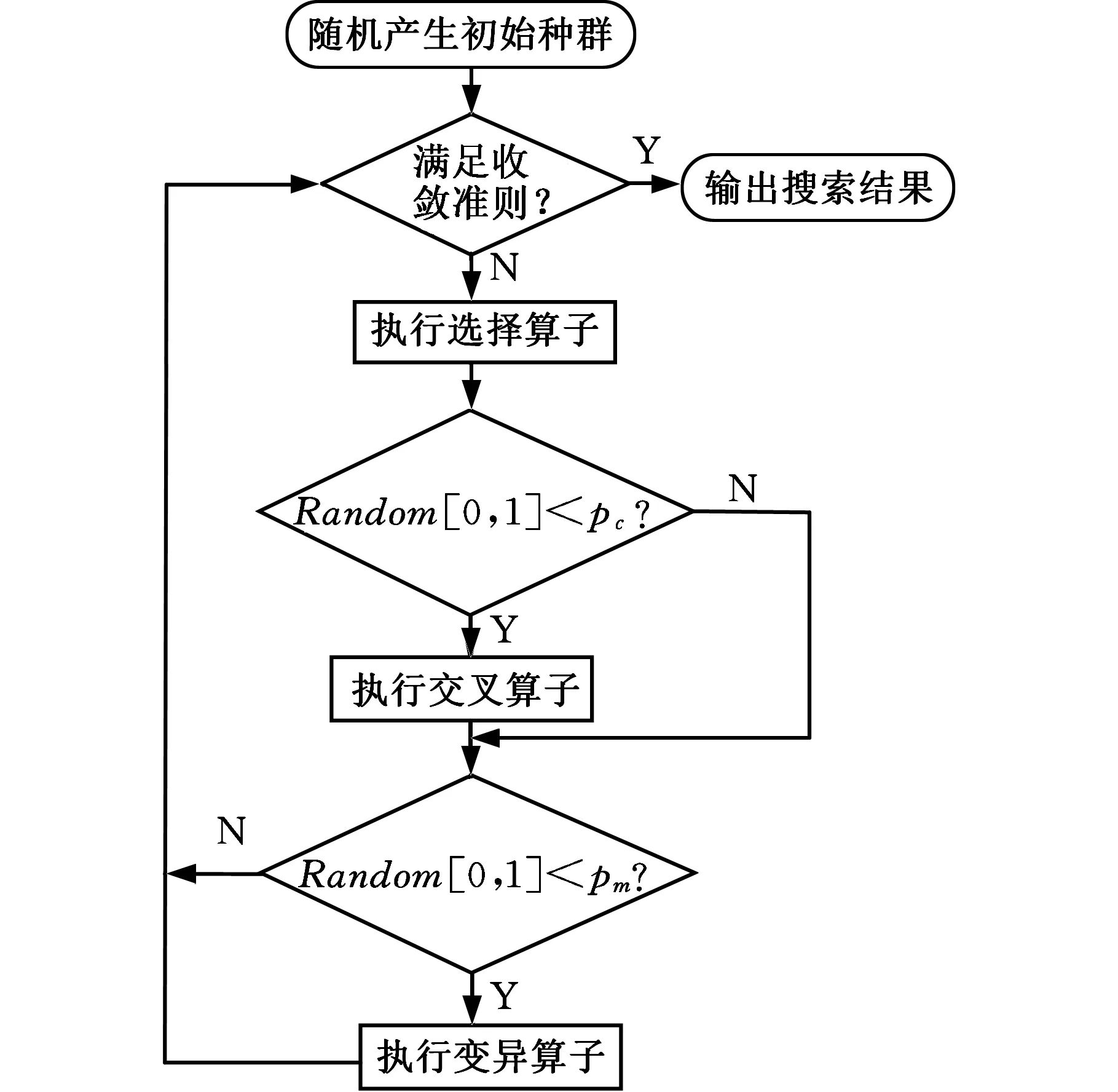
图1 遗传算法步骤Fig.1 The genetic algorithm steps

2 实例分析

2.1汽车空调压缩机制冷量Q与关键零部件尺寸关系

在给定工况的条件下，压缩机的制冷量Q0主要由压缩机的排量V决定，本文研究的SD7V16型车载空调压缩机的关键机构示意图见图2。由SD7V16关键机构的运动学分析可知：排量V由摇摆斜盘式传动机构的关键零部件尺寸、斜盘倾斜角决定。在实际工作过程中，压缩机7个活塞的正背面均受到气体压力的作用，当正背面气体压力平衡时，斜盘组件以稳定的斜盘倾斜角高速运转，当通过调控控制阀来改变曲轴箱内压力时，活塞正背压力合力产生的力矩发生变化，从而改变斜盘倾角的大小，可最终实现对排量的控制。假定SD7V16关键机构保持最大斜盘倾斜角α=24°不变，则排量V仅由摇摆盘铰接中心分布圆半径r、双球头连杆两端球头中心距l、摇摆盘厚度h、气缸中心分布圆半径R、活塞直径D这5个关键尺寸与公差所决定,而在给定工况下，压缩机实际功率一定，斜盘倾斜角不变(α=24°)时，制冷量Q0可认为仅由排量V决定，故可视为制冷量Q0仅与R、r、h、l、D这5个关键尺寸相关。

图2 SD7V16关键机构示意图Fig.2 Key institutions schematic of SD7V16

2.2关键零部件公差成本建模

2.2.1加工成本模型

设r、l、h、R、d优化后的加工公差分别为T1、T2、T3、T4、T5。先根据各个公差的特征类型选取合适的加工公差成本模型。其中,T1、T2选定位特征尺寸的公差成本函数;T3选平面特征尺寸的公差成本函数；T4选内孔特征尺寸的公差成本函数；T5选外圆特征尺寸的公差成本函数。那么SD7V16型压缩机关键零部件总加工成本为

(16)

2.2.2质量损失成本模型

表1所示为关键零部件尺寸公差与报废成本之间的关系。由优化后的尺寸公差Ti造成的质量损失成本为

(17)

式中，Ai为报废成本。

SD7V16各关键零部件公差总的质量损失成本为

(18)

表1 关键零部件尺寸公差与报废成本Tab.1 Key parts size tolerance and scrap cost

2.3标准工况条件的确立

设摇摆盘铰接中心分布圆半径偏差为Δr，双球头连杆两端球头中心距偏差为Δl，摇摆盘厚度偏差为Δh，气缸中心分布圆半径偏差为ΔR，活塞直径偏差为ΔD。引入尺寸偏差到活塞行程、压缩机排量方程中[11]，可得到活塞行程偏差方程和压缩机排量偏差方程分别为

ΔS=S1(α)-S(α)

(19)

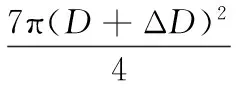
(20)

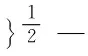
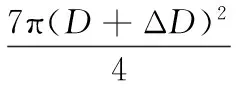
式中，S(α)为活塞行程。

压缩机在理论规定的工况下运行时制冷量为Q0，Q0由容积效率ηV、活塞直径D、活塞行程S、压缩机转速n、汽缸数z、蒸发器进出口焓差h1-h2、吸气质量体积V1所决定，其计算公式为

(21)

式中，q0为单位质量制冷量；M为气体质量。

由运动学分析可知，活塞行程S、活塞直径D与压缩机排量V的函数关系为

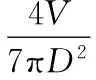
(22)

把式(22)代入式(21)可得在规定工况下制冷量Q0与压缩机排量V的函数关系式为

(23)

式中，λ为吸气系数。

当压缩机排量偏差为ΔV时，制冷量偏差

(24)

那么可以定义：在某稳定工况下以压缩机在最大斜盘倾斜角α=24°时的制冷量作为衡量SD7V16产品制冷性能的唯一参数。拟定合理的SD7V16压缩机标准工况条件[12]，如表2所示。则可以根据式(24)求解出该标准工况条件下的制冷量偏差ΔQ0。

表2 压缩机标准工况条件Tab.2 Compressor working conditions of the standard

SD7V16变排量压缩机的制冷量是根据汽车室内热负荷变化进行调节的。已知尺寸偏差，通过计算24°斜盘倾斜角时SD7V16在已知标准工况条件下的最小、最大制冷量偏差,可以为该标准工况下的尺寸公差优化提供制冷量偏差的数值约束。

根据求解的方程，代入关键零部件尺寸与最大尺寸偏差数据，可以求出ΔQ0max,即

在稳定工况下，排量偏差会直接导致制冷量偏差的产生。当尺寸偏差为最大极限尺寸偏差，即为T/2时，制冷量偏差达到最大，求得ΔQ0max=17.565 W；当不存在尺寸偏差时制冷量偏差最小,即ΔQ0min=0。

2.4公差优化模型

综上所述，为了解决SD7V16关键零部件的公差分配问题，建立考虑制冷量偏差约束的公差优化设计模型如下。

变量：

T={T1,T2,T3,T4,T5}

目标：

minF(T)=CM(T)+Ci(T)

加工能力约束:

性能要求约束：

2.5遗传算法求解与结论分析

基于MATLAB遗传算法对优化模型求解，取种群大小n=50，进化代数取50，离散精度取0.01，交叉概率pc=0.92，变异概率pm=0.04。程序经过调试后逐渐趋于稳定，经过27次迭代后，得到最稳定解如图3所示，其中目标值F(T)=21.635。

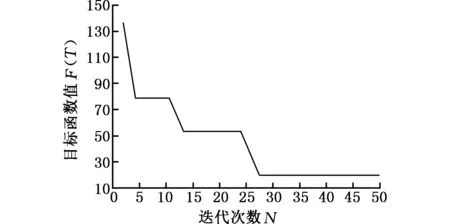
图3 优化迭代过程曲线Fig.3 The process curve of optimization iteration

由图3可知，考虑24°倾斜角制冷量偏差的公差优化模型是有效的，优化后的公差总成本比优化前成本低。具体公差与成本的对比数据见表3。

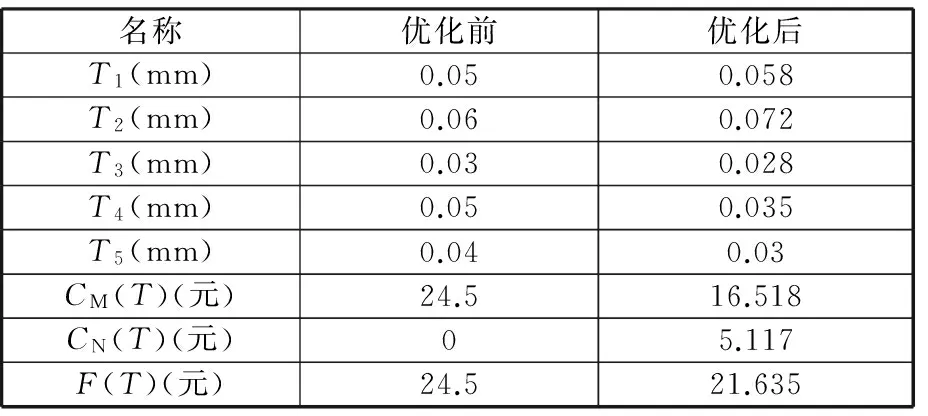
表3 优化前后结果对比Tab.3 Results compared before and after optimization

由两组数据结果对比可知，考虑质量损失与产品制冷量偏差约束的公差优化分配方案相对原公差分配方案公差总成本减少了2.865元，节省了公差总成本约11.7%。在具体公差分配过程中，将T1、T2适当增大，而将T3、T4、T5适当减小，可以在满足制冷性能约束与经济加工精度约束的条件下，实现产品的质量损失成本与加工成本之和达到最小的公差优化目标。

3 结语

产品性能的偏差值越小，则产品输出稳定性越好。许多性能偏差值往往与产品的关键零部件公差紧密相关，故零部件关键特征的公差优化设计过程中，性能偏差与关键零部件尺寸公差的函数关系可作为性能约束方程。本文在综合考虑性能偏差约束、经济加工精度约束下，建立求解最小公差总成本的优化模型。以SD7V16型车载空调压缩机为例进行分析， 验证了所建模型的有效性。

[1] 杨将新,吴绍同.机械加工成本-公差建模技术的研究[J].浙江大学学报(自然科学版)1996,30(5):517-522. YANG Jiangxin, WU Shaotong. Machining Cost-tolerance Modeling Study[J]. Journal of Zhejiang University (Natural Science Edition),1996,30(5):517-522.

[2] 任怀伟,黄克正,孙晓燕,等.概念设计中的三维公差与结构同步设计研究[J].中国机械工程,2008,19(2):226-230. REN Huaiwei, HUANG Kezheng, SUN Xiaoyan, et al. Concept Design of the Structure of Three Dimensional Tolerance and Synchronization Design Study [J]. China Mechanical Engineering,2008,19 (2):226-230.

[3] 彭和平,蒋向前,徐振高,等.基于多重相关特征质量损失函数的公差优化设计[J].中国机械工程,2008,19(5):590-594. PENG Heping, JIANG Xiangqian, XU Zhengao, et al. Based on the Multiple Correlation Characteristics of Quality Loss Function of Tolerance Optimization Design[J]. China Mechanical Engineering,2008,19(5):590-594.

[4] 黄美发,徐振高,李柱.一种工序公差的并行优化分配方法[J].工程设计,2000(4):39-42. HUANG Meifa, XU Zhengao, LI Zhu. A Parallel Process of Tolerance Optimization Allocation Method[J]. Journal of Engineering Design,2000(4):39-42.

[5] 张根保,刘帅帅,张鹏,等.质量损失拓展模型及其经济型分析[J].中国机械工程,2009,20(17):2094-2099. ZHANG Genbao, LIU Shuaishuai, ZHANG Peng. Mass Loss Expansion Model and Its Economical Analysis[J]. China Mechanical Engineering,2009,20(17):2094-2099.

[6] 胡洁.基于变动几何约束网络的形位公差设计理论与方法的研究[D].杭州:浙江大学,2001. HU Jie. Change the Form of a Geometric Constraint Network of Tolerance Design Theory and Method Research[D]. Hangzhou: Zhejiang University,2001.

[7] 罗炎旺. 车载空调压缩机的运动精度分析与公差优化设计[D]. 湘潭：湖南科技大学，2016. LUO Yanwang. Automotive Air Conditioning Compressor Motion Accurcy Analysis and Tolerance the Optimization Design[D]. Xiangtan: Hunan University of Science and Technology,2016.

[8] TAGUCHI G,WU Y. Introduction to Off-line Qu-ality Control[R]. Nagoya, Japan: Central Japan Quality Control Association,1985.

[9] 张俊.微电机关键零部件公差设计建模与优化[D]. 湘潭:湖南科技大学,2012. ZHANG Jun. The Key Components of Themicromotor Tolerance Design Modeling and Optimization[D]. Xiangtan: Hunan University of Science and Technology,2012.

[10] 费业泰.误差理论与数据处理[M].北京:机械工业出版社,2004:55-56. FEI Yetai. Error Theory and Data Processing[M]. Beijing: Mechanical Industry Press,2004:55-56.

[11] 郭来红.XL7V16变排量压缩机开发研究[D].合肥:合肥工业大学,2012. GUO Laihong. XL7V16 Variable Displacement Compressor Development Research[D]. Hefei: Hefei University of Technology,2012.

[12] 廖云飞.斜板式变排量压缩机及其汽车空调制冷系统特性研究[D].北京:清华大学,2004. LIAO Yunfei. Inclined Plate Type Variable Displacement Compressor and Automotive Air Conditioning Refrigerating System Characteristics Research[D]. Beijing: Tsinghua University,2004.

(编辑王艳丽)

ConstraintToleranceOptimizationDesignBasedonPerformanceDeviation

GUO Yingfu1LUO Yanwang1ZHAO Yanming2HE Hongxi1TAN Huajiang1

1.Hunan Provincial Key Laboratory of Health Maintenance for Mechanical Equipment, Hunan University of Science and Technology, Xiangtan,Hunan,411201 2.School of Information and Electrical Engineering,Hunan University of Science and Technology,Xiangtan,Hunan,411201

Based on the actual production processes, there were many factors that affected the processing costs, it was difficult to use a unified mathematical model to accurately describe all types of processing costs-tolerance relationships, the product processing costs and the quality loss costs were regared as targets, the product tolerance optimization model was established and with the restriction of product performance deviation and economic machining precision. GA was used to solve them, and finally a type of automotive air conditioning compressor was to be an example to verify the validity of the model.

tolerance cost; performance deviation; genetic algorithm(GA); tolerance optimization

2016-06-21

国家自然科学基金资助项目(51175171)

TH124

10.3969/j.issn.1004-132X.2017.17.009

郭迎福，男，1962年生。湖南科技大学机电工程学院教授。主要研究方向为机械设计、信号测试与故障诊断。发表论文50余篇。E-mail：604442263@qq.com。罗炎旺，男，1990年生。湖南科技大学机电工程学院硕士研究生。赵延明，男，1973年生。湖南科技大学信息与电气工程学院副教授。何鸿曦，男，1992年生。湖南科技大学机电工程学院硕士研究生。谭华江，男，1992年生。湖南科技大学机电工程学院硕士研究生。