图案化介质磁盘-磁头气体润滑动态特性分析

杨利花 杨 凯 徐郝亮 虞 烈

1.西安交通大学机械结构强度与振动国家重点实验室,西安,7100492.陕西省先进飞行器服役环境与控制重点实验室,西安,710049

图案化介质磁盘-磁头气体润滑动态特性分析

杨利花1,2杨 凯1徐郝亮1虞 烈1

1.西安交通大学机械结构强度与振动国家重点实验室,西安,7100492.陕西省先进飞行器服役环境与控制重点实验室,西安,710049

在小扰动条件下，提出应用偏导数法在复数域内求解可压缩气体润滑的动态Reynolds方程，以计算任意磁盘表面形状的磁盘-磁头气膜润滑的动态刚度和阻尼系数。以圆柱形和立方形比特图案化介质(BPM)磁盘为研究对象，研究了磁单元尺寸参数对气膜动态系数的影响，并比较了两种BPM对应的动态性能。数值结果表明，与光滑磁盘相比，图案化介质磁盘对应的气膜润滑动态刚度系数和阻尼系数大大减小,且随磁单元高度增大，动态系数逐渐减小。相比圆柱形BPM，立方形BPM对应的气膜具有较大动态刚度和阻尼系数，计算结果可为图案化介质磁盘的设计提供重要的理论依据。

比特图案化介质；计算机磁盘；存储密度；动态性能

0 引言

随着磁盘存储密度的不断增大，磁头与磁盘间隙(即飞行高度)越来越小，可能发生的磁头磁盘界面接触和凸峰冲击等都会影响磁头的飞行稳定性和读写可靠性,因此，精确估计磁头超薄气膜润滑的动态特性对提高磁盘存储密度和读写可靠性至关重要。

分析磁头气膜的动态特性需要求解超薄气体润滑Reynolds方程和磁头系统的运动方程。HONCHI等[1]建立了包含简化悬臂支架模型、气膜润滑模型和磁头-磁盘接触模型的系统动力学分析模型，采用有限差分法同步求解气体润滑Reynolds方程和磁头的运动方程，研究了磁头-磁盘接触过程中的磁头振动模态。ZENG等[2-3]应用开发的动态求解器求解小扰动下磁头浮动块的振动响应，后又通过模态分析法获得磁头-磁盘系统的模态参数以及刚度和阻尼系数。ONO[4]通过小扰动法和有限差分法在频域计算了气膜的动态压力分布，分析了不同表面形貌浮动块的气膜动态系数及动态响应，重点研究了扰动频率对气膜动态刚度和阻尼的影响。MITSUYA等[5]推导了与粗糙度方向相关的气膜动态润滑方程，并用有限元法求解了动态润滑方程,得到了气膜动态刚度和阻尼系数，研究了粗糙度方向和大小、扰动频率、磁盘速度和载荷对动态系数的影响。LI等[6]在小扰动假设下用频率响应法计算了三自由度磁头系统的气膜刚度和阻尼系数，分析了不同浮动块表面结构对应的气膜动态系数随扰动频率的变化关系，提出改进磁头阻尼的设计方案。庄苹等[7]应用伽辽金法和有限元法求解了动态Reynolds方程，并进行了磁头-磁盘系统的动态响应分析，研究了粗糙度方向对磁头飞行稳定性的影响。王玉娟等[8]利用摄动法建立气体润滑的静动态Reynolds方程，采用交换方向法研究了气膜动态刚度和阻尼与最小膜厚、磁盘转速和磁头倾角的关系。 白少先等[9]采用摄动法进行气体润滑频域响应分析，讨论了气膜刚度和阻尼等随飞行高度和扰动频率的变化规律，可用于指导磁头/磁盘系统的设计。

以上关于磁头/磁盘系统气膜动态性能的研究，均是针对飞行在连续或光滑表面磁盘上的磁头开展的。随着更高磁盘存储密度的需求，西部数据公司(western digital company, WD)等磁盘制造商近年来一直致力于比特图案化介质(bit pattern media, BPM)磁盘的制备与研发[10]。这种磁盘表面不再是光滑的连续表面，而是由制备在其上的多个独立的有序图案化磁单元排列构成的离散表面，磁盘表面与磁头上的浮动块表面间形成动压气膜，气膜的静态和动态性能对磁盘的存储性能有重要影响。LI等[11-12]分析了图案化介质磁盘形状和参数对浮动块飞行高度、气膜压力等静态性能的影响。张延瑞等[13]以三维凸台气膜润滑模型模拟图案化介质磁盘表面，研究了气膜压力与凸台高度和最小间隙的关系，以讨论图案化介质磁盘-磁头系统的气体润滑静态性能。LI等[14]应用有限元分析方法研究了浮动块和图案化介质磁盘界面间的接触状态、材料特性以及不同充填材料下图案化介质的平坦化对磁盘塑性变形和温度的影响。此类磁盘因具有超高的存储密度和较好的读写稳定性而成为近年来的发展目标，但由于其制备的困难以及高成本而限制了其应用。

现有文献的研究方法多数是在频域内计算非BPM磁盘表面和磁头浮动块表面间的气膜动态刚度和阻尼，以避免对与时间相关的气膜润滑动态Reynolds方程的直接求解，而本文拟在小扰动假设下，提出采用偏导数法在复数域内直接求解气体润滑的动态Reynolds方程，避免了求解中的时间相关性，以计算气膜润滑的动态刚度和阻尼系数。偏导数法可适用于任何表面形貌的磁盘和磁头间气膜润滑动态刚度和阻尼的计算。本文分别以圆柱形和立方形图案化磁盘为研究对象，给出了对应计算结果,并研究了磁单元形状和尺寸参数对图案化介质磁盘-磁头的气膜动态特性的影响。

1 数学模型

1.1超薄气体润滑方程

超高密度磁记录系统中，磁头和磁盘间的气膜间隙一般小于气体分子的平均自由程的100倍，需要引入修正系数以计入气体分子滑移效应对气膜压力的影响，DUWENSEE[15]给出了三种修正系数计算公式,其中一阶修正的修正系数为

Q1=1+6Kn

二阶修正的修正系数为

Boltzmann修正的修正系数为

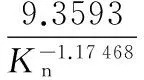
(1)

Kn=λ/h

式中，Kn为表征气体稀薄程度的Knudsen数；λ、h分别为气体分子的平均自由程和气膜厚度。

本文计算采用 Boltzmann修正系数。建立图1所示三自由度坐标系，引入修正系数后的超薄气膜润滑量纲一Reynolds方程形式为

(2)

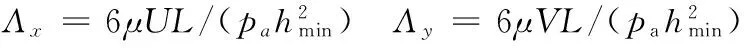
式中，p为有量纲气膜压力;h为有量纲气膜厚度;P、H分别为量纲一气膜压力和厚度;hmin为最小气膜间隙或飞行高度；pa为环境大气压力；X、Y分别为浮动块长度和宽度方向的量纲一坐标;L为磁头浮动块长度；x、y为有量纲坐标；Λx、Λy为轴承数；μ为气体动力黏度；U、V分别为浮动块相对于磁盘在长度和宽度方向的飞行速度(本文计算中U为对应磁盘径向位置的线速度，V=0)；T为量纲一时间;ω为磁盘角速度；t为时间；σ为压缩数。

磁头浮动块气膜润滑量纲一气膜厚度为

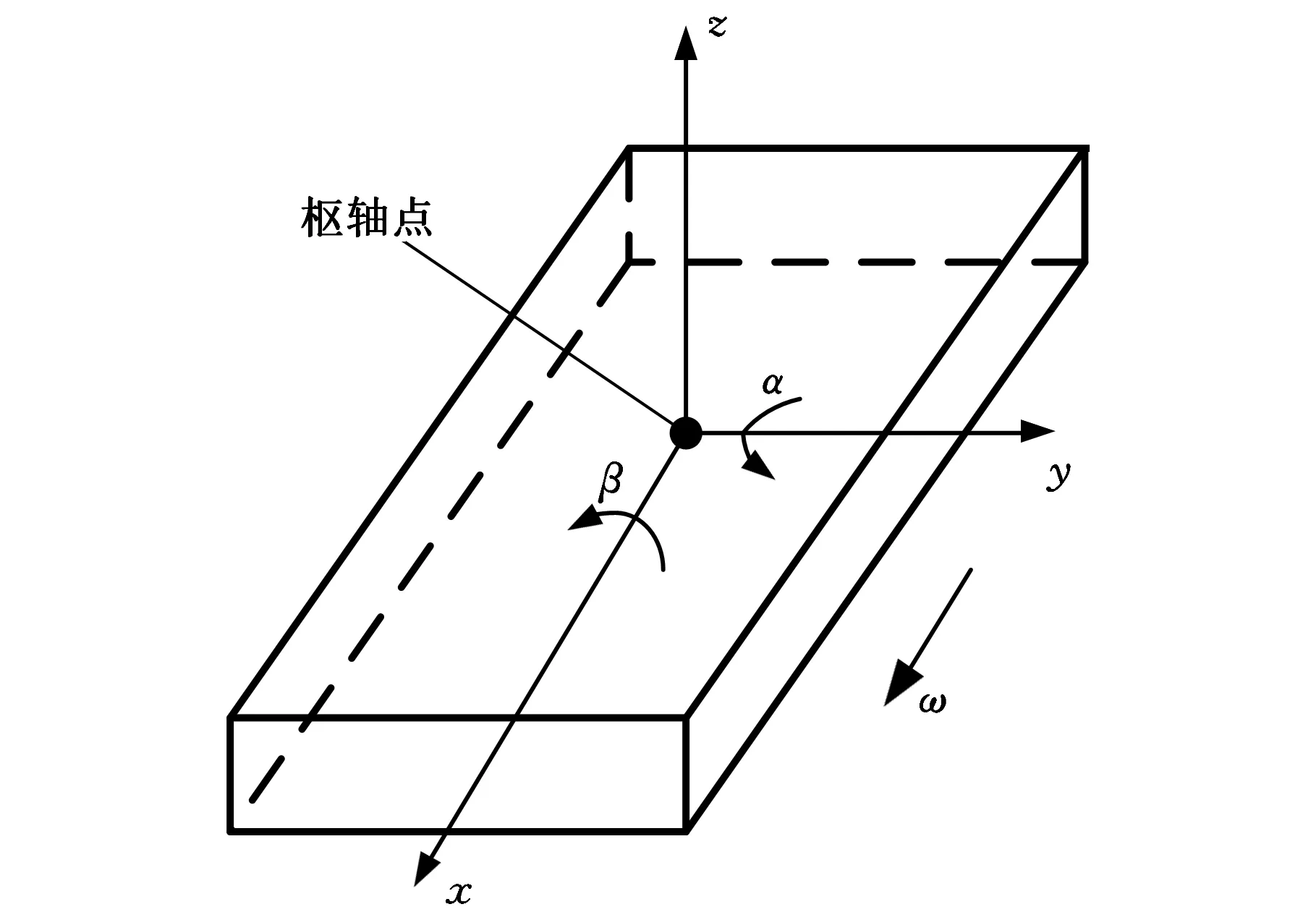
图1 磁头浮动块坐标系Fig.1 Coordinate system of slider

(3)

Z=z/hminXp=xp/LYp=yp/L

式中，Z为浮动块垂直方向的量纲一坐标；z为有量纲纵向坐标；α、β分别为俯仰角(pitch角)和翻转角(roll角)；Xp、Yp为枢轴点的量纲一坐标；xp、yp为枢轴点有量纲坐标。

应用有限差分法和牛顿-拉普森迭代法同时迭代求解超薄气膜润滑的静态Reynolds方程和浮动块的力和力矩平衡方程，就可获得浮动块在特定工况时的静态平衡位置及气膜压力和气膜厚度分布[16]。

1.2气膜动态性能计算[17]

采用小扰动法，假设浮动块绕其静态平衡位置发生周期性小扰动，任意时刻的浮动块位置可以表示为

(4)

Ω=ν/ω

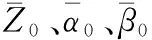
同样利用小扰动假设，可将气膜压力P和气膜厚度H表示为静态项和动态项，其形式为

(5)

(6)

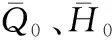
将式(4)代入式(5)，并忽略无穷小项，得到任意时刻的气膜厚度为

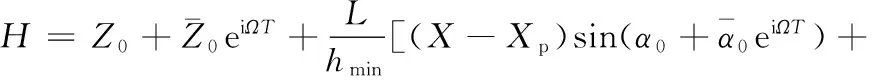
(7)

则动态气膜厚度扰动幅值为

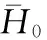
(8)

将式(5)和式(6)代入动态Reynolds方程(式(2))，利用静态Reynolds方程化简并忽略高阶无穷小量，得到小扰动时超薄气体润滑的动态Reynolds方程如下：

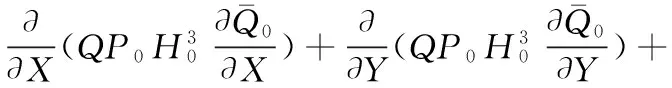
(9)

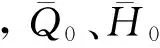
关于QZ和HZ的方程为

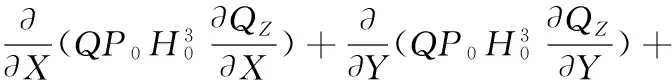
(10)

HZ=1

(11)

由于QZ和HZ为复变量，可令QZ=QZR+iQZI，HZ=HZR+iHZI，代入式(10)，则可得到关于QZR、QZI的实部和虚部方程，并将它们化成如下椭圆型偏微分方程-·(cu)+au=f形式：

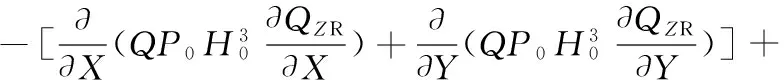
(12)

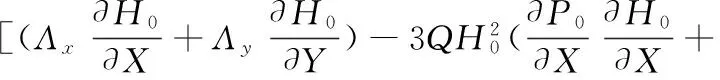
(13)

应用MATLAB的偏微分方程PDE工具箱同时迭代求解式(12)和式(13)， 就可得到QZ的解。

同理，可得到Qα和Qβ的偏微分方程并求得其结果，其中Hα和Hβ有如下形式：

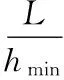
(14)

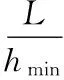
(15)

求得QZ、Qα和Qβ后, 则浮动块表面气膜的量纲一动态刚度和阻尼系数为

(16)

m=z,α,β

对应的动态系数为

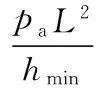
[8][32][48] 范子英、彭飞、刘冲：《政治关联与经济增长：基于卫星灯光数据的研究》，《经济研究》2016年第1期，第114-126页。

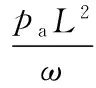
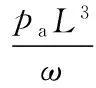
对三自由度浮动块气膜润滑而言，应用小扰动法可得到其9个刚度系数kij(i,j=z，α，β)和9个阻尼系数dij，由于偏导数法消除了Reynolds方程中的时间项，将问题转换到复数域进行求解，从而大大降低了求解的复杂性和速度。

应用这些动态刚度和阻尼系数，可以得到气膜润滑的动态气膜力和力矩矩阵表达形式如下:

(17)

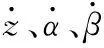
2 结果与分析

2.1气膜动态性能计算

图2所示为磁头上的浮动块几何模型及表面形貌，可以看出浮动块工作表面并非光滑。浮动块长度L=850 μm，宽度B=700 μm，磁头和浮动块连接的枢轴点位于浮动块几何中心位置。图3给出了磁盘上两种不同图案化磁单元形状的结构模型及参数，即圆柱形和立方形图案化介质BPM，以研究磁单元形状对气膜动态特性的影响。其中，b为相邻磁单元边距，d为圆柱形磁单元直径或立方形磁单元边长，hb为磁单元高度，w为相邻磁单元间距,w=b-d。磁盘工作过程中，图2浮动块工作表面和图3的BPM表面间会形成动压气膜润滑。

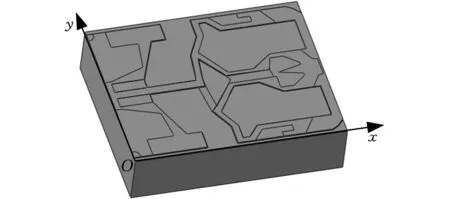
图2 浮动块几何模型及表面形貌Fig.2 Geometrical model and surface topography of slider

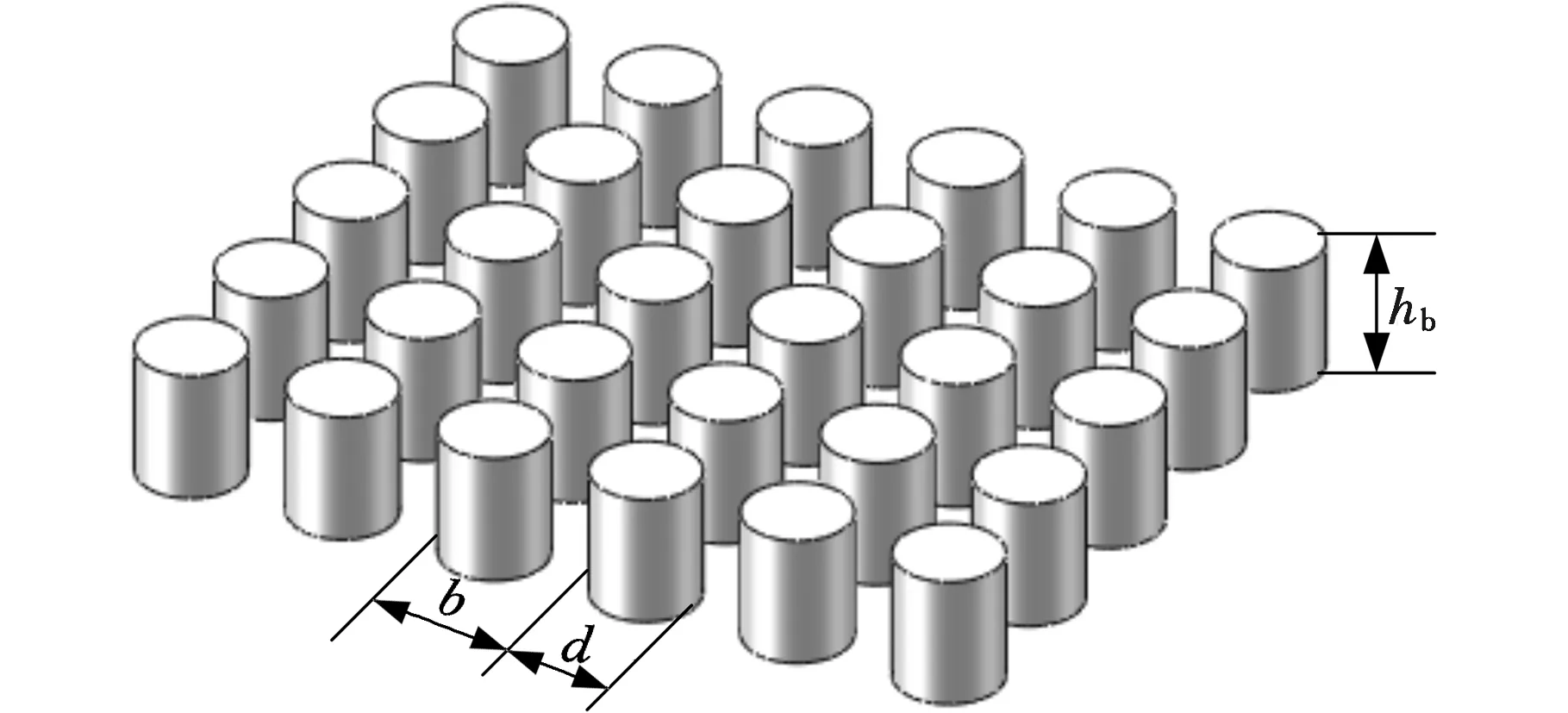
(a)圆柱形BPM

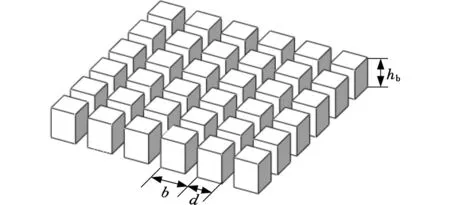
(b)立方形BPM图3 BPM磁盘模型Fig.3 BPM model

本文所研究的磁盘-磁头浮动块表面间的润滑气体采用含有98%氦气的空气-氦气混合工质，动力黏度μ=2.018×10-5kg/(m·s)，密度ρ=0.1801 kg/m3，环境压力pa=65.86 kPa, 气体分子平均自由程λ=190 nm。

2.2BPM尺寸对气膜润滑动态性能的影响

本文所研究的磁盘-磁头在浮动块长度方向线速度U=20 m/s，通过有限元分析获得悬臂支架刚度，分别为kz=20 N/m，kα=kβ=3.5×10-5N·m/rad。枢轴点坐标位置为xp=425 μm，yp=350 μm时，通过求解静态Reynolds方程和浮动块的力平衡方程计算了空气-氦气混合工质下图案化介质磁盘对应的浮动块表面静态压力和厚度分布，其后在小扰动假设下应用上述偏导数法求解了不同磁单元尺寸对应的气膜润滑动态系数。由于动态系数的交叉项相对于直接项很小，故本文只讨论气膜润滑的直接动态系数。

图4是不同磁单元尺寸的立方形图案化介质BPM对应的气膜动态刚度系数和阻尼系数随磁单元高度的变化规律曲线。从图4可以看出，由于气膜厚度方向(Z向)为主要承载方向，故其对应刚度系数和阻尼系数远大于其他两个方向的刚度系数和阻尼系数。与磁单元高度为零的光滑磁盘相比，图案化介质BPM使气膜润滑的动态系数大大降低，其中kzz降低了大约6倍。随磁单元高度增大，所有的刚度系数和阻尼系数均呈微小减小趋势。对于具有相同磁单元尺寸比b/w=2的两种参数b=10 μm,w=5 μm和b=1.2 μm,w=0.6 μm而言，它们对应的动态系数也几乎相同。而较大的b/w值则对应较大的动态刚度系数kzz、kαα、kββ和阻尼系数dββ，特别对较大b/w值的b=1.2 μm,w=0.3 μm而言，其刚度系数和阻尼系数明显比其他参数时大。这些结果可为图案化介质磁盘的设计提供理论参考。而且结果表明，尽管图案化介质磁盘能够提高磁盘的存储密度，但它会降低气膜润滑的动态性能。这是因为浮动块表面的气膜压力主要分布在它与图案化磁单元表面对应区域，而与磁单元间隙对应区域的气膜压力很小[16]。因此与连续光滑表面磁盘相比，图案化介质磁盘因对应的有效气膜压力作用面积减小，使浮动块表面的气膜合力减小，从而降低了对应气膜润滑的动态性能。且磁单元高度增大不会影响有效气膜压力作用面积，只会使与磁单元间隙对应区域的气膜压力有微小减小，因此磁单元高度变化对气膜动态性能的影响很小。

图5是磁单元尺寸为b=1.2 μm,w=0.3 μm时，圆柱形和立方形BPM对应的气膜润滑动态系数随磁单元高度的变化曲线。结果表明，在此磁单元尺寸下，随磁单元高度增大，圆柱形和立方形BPM对应的气膜润滑的6个直接刚度系数和阻尼系数均逐渐减小。与圆柱形BPM相比，立方形图案化介质对应的气膜具有较大的刚度和阻尼系数。也就是说，立方形BMP对应的浮动块具有比圆柱形BMP更优越的动态性能。这是由于当圆柱形磁单元直径与立方形磁单元边长相同时，立方形磁单元对应的有效气膜压力作用面积大于圆柱形磁单元对应的有效气膜压力作用面积，因而立方形磁单元对应的浮动块表面气膜合力较大,所以立方体磁单元的动态性能更优。

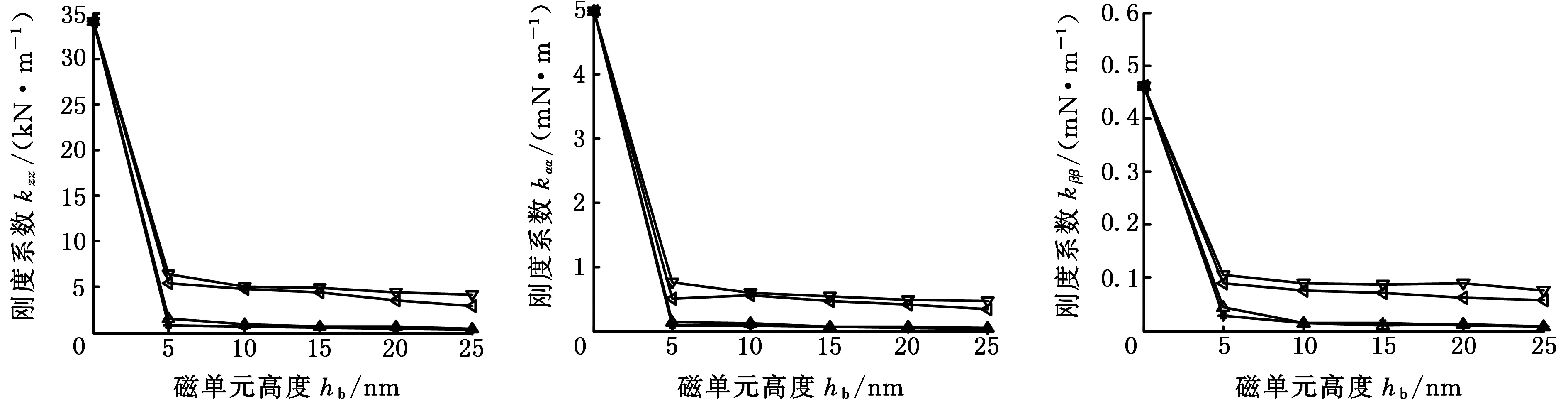
(a)刚度系数kzz (b)刚度系数kαα (c)刚度系数kββ

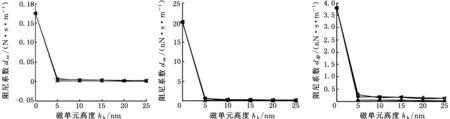
(d)阻尼系数dzz (e)阻尼系数dαα (f)阻尼系数dββ

图4 立方形BPM对应气膜润滑动态性能随磁单元高度变化
Fig.4 Changes of dynamic coefficients of air bearing over cuboidal bit pattern media with bit height

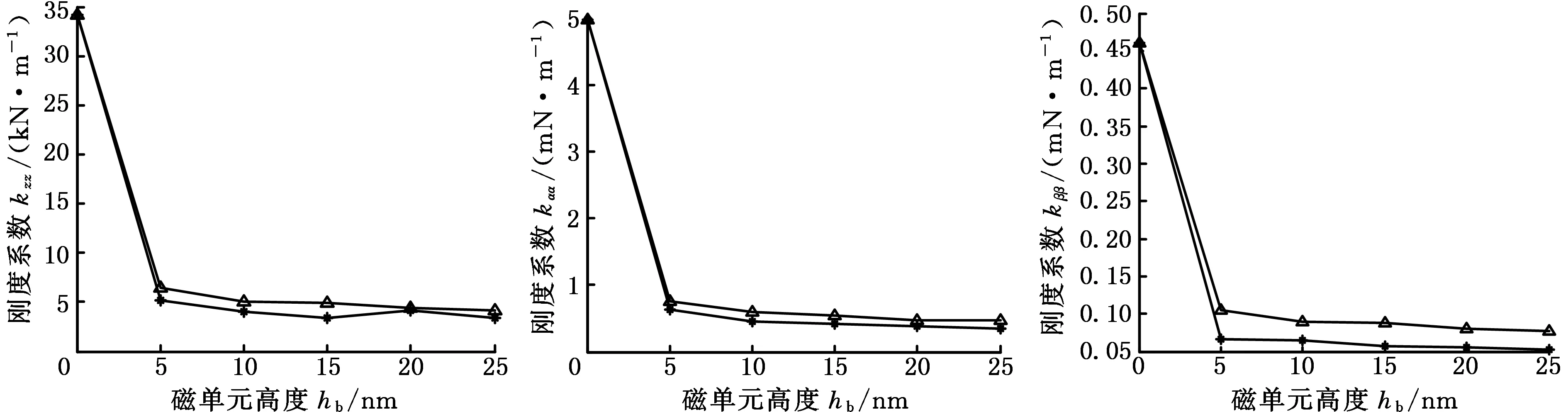
(a)刚度系数kzz (b)刚度系数kαα (c)刚度系数kββ

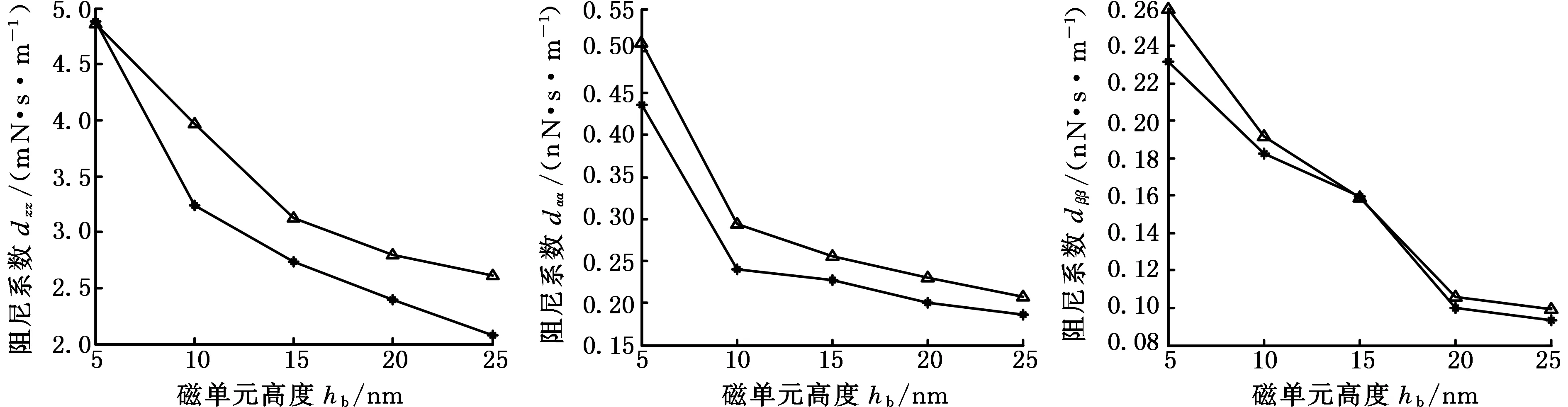
(d)阻尼系数dzz (e)阻尼系数dαα (f)阻尼系数dββ

图5 立方形和圆柱形BPM对应浮动块动态性能比较
Fig.5 Comparison of dynamic coefficients for air bearing over cylindrical and cuboidal bit pattern media

3 结论

(1)在小扰动假设下提出采用偏导数法在复数域内求解浮动块的气膜润滑动态Reynolds方程，避免了方程中时间项的求解。此方法可用于具有任意表面形状的磁盘-磁头气膜润滑动特性分析，具有普遍适用性。应用此方法分别计算了圆柱形和立方形图案化磁盘介质对应的气膜润滑动态系数，研究了磁单元结构和尺寸参数对动态系数的影响。

(2) 相比光滑磁盘表面，无论立方形还是圆柱形图案化介质，因其对应的有效气膜压力作用面积减小使气膜合力降低，从而造成气膜润滑刚度系数和阻尼系数均大大减小，且随磁单元高度增大稍有减小。

(3)因磁单元尺寸相同时，立方形图案化介质对应的有效气膜压力作用面积大于圆柱形图案化介质对应的有效气膜压力作用面积，因此其对应的气膜具有比圆柱形 BPM更大的刚度系数和阻尼系数，表明立方形BPM比圆柱形BPM具有更好的动态性能，可为图案化介质磁盘的设计提供重要的理论依据。

致谢本文研究工作是在美国加州大学圣地亚哥分校(University of California, San Diego)磁记录研究中心(Center for Memory and Recording Research)Frank E. Talke教授的精心指导下和研究生的大力帮助下完成的，在此表示衷心感谢!

[1] HONCHI M, KOHIRA H, MATSUMOTO M. Numerical Simulation of Slider Dynamics during Slider-disk Contact[J]. Tribolology International,2003,36:235-240.

[2] ZENG Qinghua, CHEN Liangsheng, BOGY D B. A Modal Analysis Method for Slider Air Bearing in Hard Disk Drives[J]. IEEE Transactions on Magnetics,1997,33(5):3124-3126.

[3] ZENG Qinghua, BOGY D B. Stiffness and Damping Evaluation of Air Bearing Sliders and New Designs with High Damping[J]. Journal of Tribology,1999,121(2):341-347.

[4] ONO K. Dynamic Characteristics of Air-lubricated Slider Bearing for Noncontact Magnetic Recording[J]. Journal of Lubrication Technology,1975,97(2):250-260.

[5] MITSUYA Y, OTA H. Stiffness and Damping of Compressible Lubricating Films between Computer Flying Heads and Textured Media: Perturbation Analysis Using the Finite Element Method[J]. Journal of Tribology,1991,113(4):819-827.

[6] LI Jianhua, XU Junguo, SHIMIZU Y, et al. Design and Evaluation of Damped Air Bearings at Head-disk Interface[J]. Journal of Tribology,2010,32(3):031702-1-13.

[7] 庄苹，王玉娟，陈云飞. 超薄气体润滑磁盘/磁头系统动力学分析[J]. 中国机械工程，2001,12(10): 1191-1194. ZHUANG Ping, WANG Yujuan, CHEN Yunfei. Ro-ughness Effects on Dynamic Response of High Density Disk Drives Under High Knudsen Number[J]. China Mechanical Engineering,2001,12(10):1191-1194.

[8] 王玉娟，陈云飞，庄苹，等. 磁头磁盘系统动特性参数及系统稳定性分析[J]. 中国机械工程，2002,13(3): 256-259. WANG Yujuan, CHEN Yunfei, ZHUANG Ping, et al. Dynamic Coefficients and Dynamic Stability in Magnetic Recording[J]. China Mechanical Engineering,2002,13(3):256-259.

[9] 白少先，彭旭东，孟永刚，等. 磁头/磁盘超薄膜气体润滑动态性能分析[J]. 应用力学学报， 2009，26(4): 685-689. BAI Shaoxian, PENG Xudong, MENG Yonggang, et al. Dynamic Character of Ultra Thin Film Gas Lubrication for Magnetic Head/Disk[J]. Chinese Journal of Applied Mechanics,2009,26(4):685-689.

[10] ALBRECHT T R, ARORA H, AYANOOR-VITIKKATE V, et al. Bit Patterned Magnetic Recording: Theory, Media Fabrication, and Recording Performance[J]. IEEE Transactions on Magnetics,2015,51(5):1-42.

[11] LI Hui, ZHENG Hao, YOON Y, et al. Air Bearing Simulation for Bit Patterned Media[J]. Tribology Letters,2009,33:199-204.

[12] LI Hui, TALKE F E. Numerical Simulation of the Head/Disk Interface for Bit Patterned Media[J]. IEEE Transactions on Magnetics,2009,45(11):4984-4989.

[13] 张延瑞，孟永刚. 基于连续模型和离散模型的微尺度三维凸台轴承的气体润滑分析[J]. 摩擦学学报，2011，31(4): 397-407. ZHANG Yanrui, MENG Yonggang. Gas Lubrication Analysis of Three Dimensional Micro Scale Gas Slider Bearings with Bumps Based on Continuum and Discrete Models [J]. Tribology,2011,31(4):397-407.

[14] LI Longqiu, SONG Wenping, ZHANG Chunhui, et al. Investigation of Thermo-mechanical Contact between Slider and Bit Patterned Media[J]. Microsystem Technologies,2012,18(9/10):1567-1574.

[15] DUWENSEE M. Numerical and Experimental Investigation of the Head Disk Interface [D]. Q. San Diego: University of California, 2007.

[16] 杨利花，徐郝亮，虞烈. 比特图案化介质磁盘-磁头的气膜静态特性研究 [J]. 西安交通大学学报，2016, 50(6): 110-115. YANG Lihua, XU Haoliang, Yu Lie. Study on Static Characteristics of Air Bearing Film over Bit Pattern Media in Hard Disk Drives[J]. Journal of Xi’an Jiaotong University,2016,50(6):110-115.

[17] YANG Lihua, QI Shemiao, YU Lie. Analysis on Dynamic Performance of Hydrodynamic Tilting-pad Gas Bearings Using Partial Derivative Method [J]. Transactions of the ASME Journal of Tribology, 2009,131(1):011703-1-8.

(编辑王艳丽)

AnalysisonDynamicCharacteristicsofAirBearingoverBitPatternMediainHardDiskDrives

YANG Lihua1,2YANG Kai1XU Haoliang1YU Lie1

1.State Key Laboratory for Strength and Vibration of Mechanical Structures,
Xi’an Jiaotong University, Xi’an, 710049 2.Shaanxi Key Laboratory of Environment and Control for Flight Vehicle, Xi’an, 710049

With the assumption of small perturbation, this paper applied the partial derivative method to solve the compressible gas-lubricated dynamic Reynolds equation in the complex domain. This method might be used to calculate air-film dynamic stiffnesses and dampings of hard disk drives with arbitrary surface topography of disks. The dynamic stiffness and damping coefficients of air bearing over bit pattern media were calculated. Moreover, the effects of bit height of cylindrical and cuboidal bit pattern media on the dynamic coefficients were studied and also the dynamic performances of two types of bit pattern media were compared. The results indicate that the dynamic stiffness and damping coefficients of air bearing over bit pattern media largely decrease compared with those over smooth disk. With the increasing of bit height, the dynamic coefficients gradually reduce. Compared with cylindrical bit pattern media, the gas bearing over cuboidal bit pattern media has larger dynamic stiffnesses and dampings. These results may provide important theoretical reference for the designs of bit pattern media.

bit pattern media; computer disk; storage density; dynamic characteristics

2017-01-23

国家自然科学基金资助项目(51575425)

TH117.2

10.3969/j.issn.1004-132X.2017.17.004

杨利花，女，1975年生。西安交通大学航天航空学院副教授。主要研究方向为摩擦学、轴承-转子动力学。发表论文50余篇。E-mail:yanglihua_2@126.com。杨凯，男，1989年生。西安交通大学航天航空学院硕士研究生。徐郝亮，男，1988年生。西安交通大学航天航空学院博士研究生。虞烈，男，1948年生。西安交通大学机械工程学院教授。