一类(1+1)维色散方程组的多项式不变子空间

张亚敏

(宝鸡文理学院 数学与信息科学学院, 陕西 宝鸡 721013)

张亚敏

(宝鸡文理学院 数学与信息科学学院, 陕西 宝鸡 721013)

不变子空间； 条件Lie-Bäcklund对称； 精确解

近些年来，随着科学技术的飞速发展，研究的不断深入，微分方程已经广泛地应用到许多科学领域中，成为研究的热点问题。而大部分偏微分方程求出精确解非常困难，只能求出近似的数值解，但方程的精确解可帮助人们分析系统内部的运动结构，因此微分方程精确解的研究吸引了许多学者，他们推出了许多求解方法，例如李点对称法、齐次平衡法、条件对称法、不变子空间法等等，但对非线性偏微分方程的精确解，没有找出具体统一、规范的求解方法。不变子空间方法是和条件Lie-Bäcklund对称相关的一种构造非线性偏微分方程精确解的有效方法，是由Titov等[1-2]首先提出，后来屈长征教授等进一步研究发展，使该方法运用于求解耦合的非线性演化方程的精确解，已经取一些有意义的结果[3-10]。

一类(1+1)维色散方程组

(1)

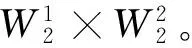
1 不变子空间方法

一般演化方程组

Vt=G[V]=(G1[V],G2[V],…,Gm[V]),

(2)

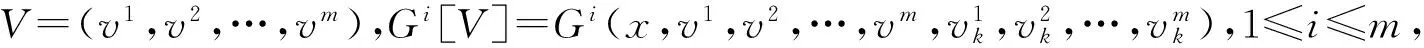
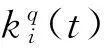
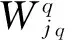
(3)

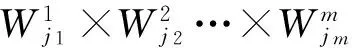
Lq[Gq[V]]|[H1]∩[H2]∩…∩[Hm]=0, 1≤q≤m,

(4)

其中[Hq]表示Lq[vq]=0及其关于x的微分结果。

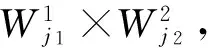
2 主要结果

方程组(1)右边的非线性算子为

(5)

的解构成的子空间，其中a0,a1,a2,b0,b1是待定常数。由不变子空间的条件(4)式可得，

(6)

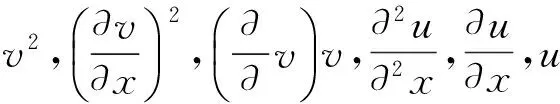
利用Maple求解上面的方程组，得出以下22种结果：

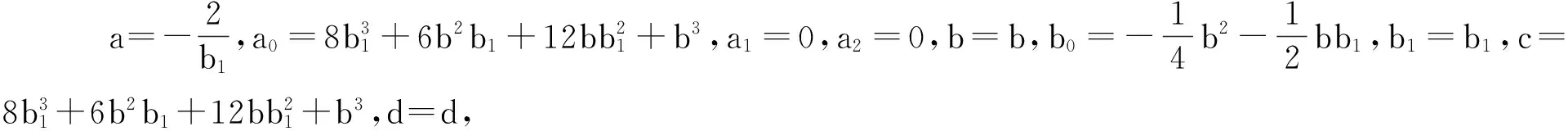
(Ⅳ) a=0,a0=a0,a1=0,a2=0,b=0,b0=b0,b1=b1,c=a0,d=d,故得

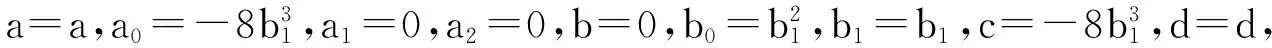
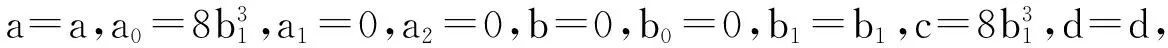
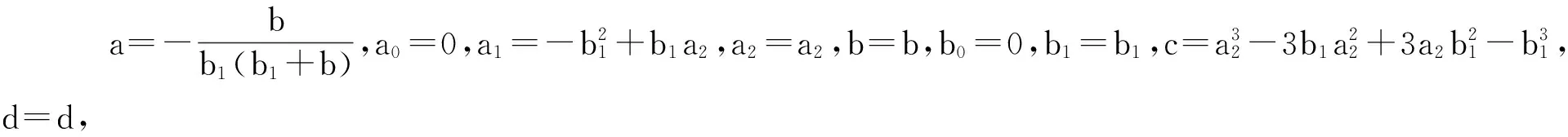
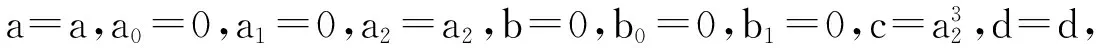
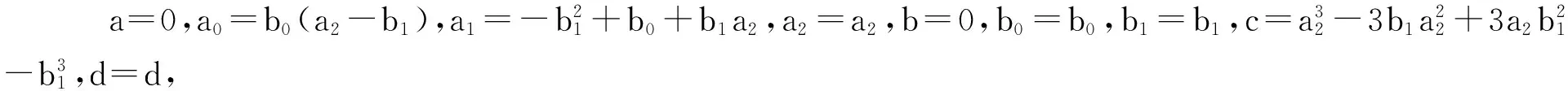
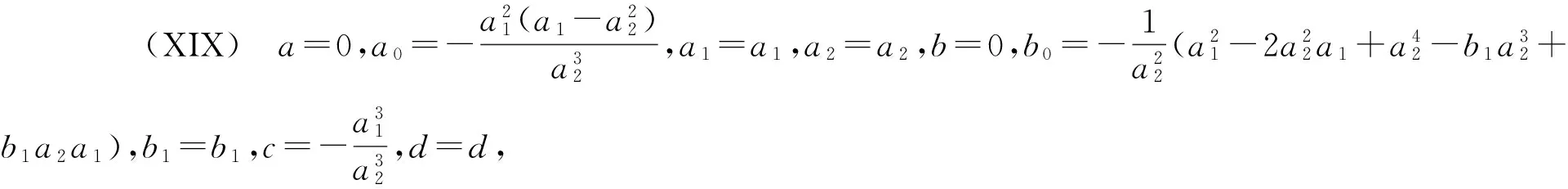
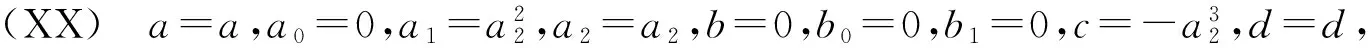
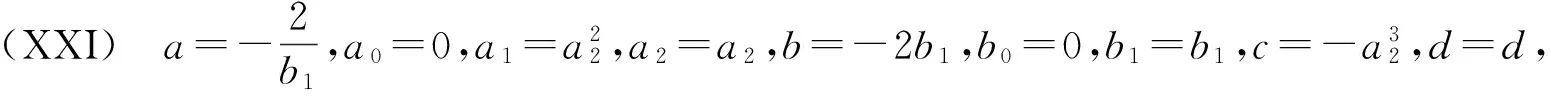
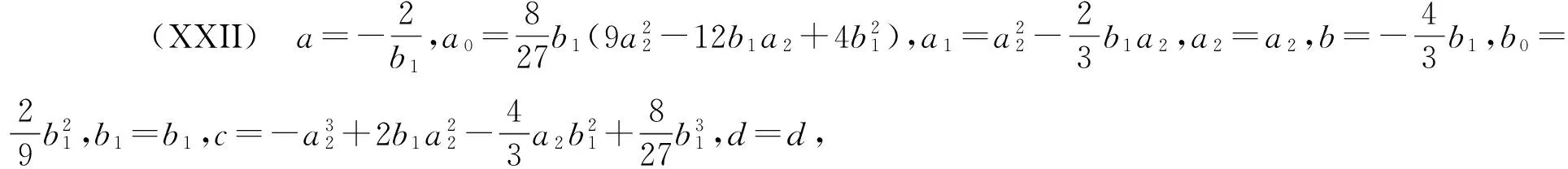
3 举例求精确解

例 方程组

满足

解 设方程组的解为

代入原方程，得

c1(t)={16k2b5t2+(4b3k4+12k3b2)t+k5}eb4t，

c2(t)=(8k3b2t+k4)eb4t,

c3(t)=k3eb4t,

d1(t)=k2edt,

d2(t)=k1edt。

故方程组的解为

u(x,t)={[16k2b5t2+(4b3k4+12k3b2)t+k5]+(8k3b2t+k4)x+k3x2}eb4t,

其中ki(i=1,2,…,6)为任意常数。

4 结 论

本文推出一类(1+1)维色散方程组允许不变子空间，在这些不变子空间上可以构造出方程组更多的精确解，通常这些解不能由古典对称法、非古典对称法等得到，这对方程组的研究奠定了一定的理论基础，另外可以考虑用不变子空间方法对非线性差分方程进行分类并求解，这也是一项有意义的研究。

[1] TILOV S S.A method of finite-dimensional rings for solving nonlinear equations of Math-emtical physics[C].Ivanova T P.Aerodyna-namics,Saratov University,1988:104-109.

[2] GALAKTIONOV V A.Geometrical properties of the solutions of one-dimensional nonlinear parabolic equations[J].Math Ann,Sect A,1995,303(4):741-769.

[3] QU C Z,ZHU C R.Classification of coupled systems with two-component nonlinear diffusion equations by the invariant subspace method[J].J Phys A,2009,42(47)：1-27.

[4] ZHU C R,QU C Z.Classification and reduction of generalized thin film equation[J].Communications in Theoretical physics,2009,52(3):403-410.

[5] QU C Z,JI L N.Invariant subspaces and conditional Lie-Backlund symmetries of inhomogeneous nonlinear diffusion equations[J].Sci China Math,2013,56(11):2187-2203.

[6] FENG W,JI L N.Conditional Lie-Backlund symmetries and functional separable solutions of generalized inhomogeneous diffusion equations[J].J Phys A,2013,392(4):618-627.

[7] SHEN S F,QU C Z,JIN Y Y.Maximal dimension of invariant subspaces to systems of nonlinear evolution equations[J].Chinese Annals of mathematics-Series B,2012,33(2):161-178.

[8] 左苏丽,李吉娜.(2+1)维拟线性抛物线方程和不变子空间[J].吉林大学学报(理学版),2011,49(1):16-20.

[9] 屈改珠.带有对流项和源项的非线性交叉扩散方程组的不变子空间及其分类[J].陕西师范大学学报(自然科学版),2015,43(5):4-8.

[10] 朱春荣,朱丹霞.可压缩欧拉方程在不变子空间中的精确解[J].工程数学学报,2016,33(3):279-286.

[11] TRACINA R,BRUZON M S.Nonlinear self-adjointness, conservation laws,exact solutions of a system of dispersive evolution equations[J].Commum Nonlinear Sci Number simulate,2014,19(9):3036-3043.

[12] MA W X,LIU Y P.Invariant subspaces and exact solutions of a class of dispersive evolution equations[J].Commum Nonlinear Sci Nume simulate,2012,17(10):3795-3801.

[责任编辑：张存凤]

Polynomial W 13 × W 22 invariant subspace to systems of ( 1 + 1) -dimensional dispersive equations

ZHANG Ya-min

( Institute of Mathematics and Information Science，Baoji University of Arts and Sciences，Baoji 721013，China )

The invariant subspace method is one of the effective methods to solve the generalized variable separation solution of nonlinear equations． A family of ( 1 + 1) -dimensional dispersive equations are considered by this method． Based on computation system Maple，a classification of the polynomial Invariant subspace W 13 × W 22 allowed by the equation is derived． More abundant exact solution of the equations are constructed by the gaining invariant subspace． Thus study has enriched the study of exact solutions of these equations， which lays the theoretical foundation for the systematic analysis of the equations described by this kind of system．

invariant subspaces; conditional Lie-Bäcklund symmetry; exact solution

2096-3998(2017)04-0081-08

2017-01-15

2017-04-10

陕西省自然科学基础研究计划项目(2014JM1027);陕西省教育厅科研计划项目(2016JK1047)；宝鸡文理学院科研项目(YK1619)

张亚敏(1978—)，女，陕西省咸阳市人，宝鸡文理学院讲师，硕士，主要研究方向为偏微分方程精确解。

O175.2

A