两个同心带电球壳体系电磁场角动量的研究

赵慧媛 阮建红

(华东师范大学物理与材料科学学院， 上海 200241)

两个同心带电球壳体系电磁场角动量的研究

赵慧媛 阮建红

(华东师范大学物理与材料科学学院， 上海 200241)

电磁场的动量和角动量是经典电磁学有趣而又基本的问题。根据标准电磁理论，电磁场角动量可表示为Lem=ε0∫vr×(E×B)dV，对恒定电磁场，角动量还可以用Lem=∫r×ρAdV来计算，文章对此进行了分析。通过一个简单的模型，即一个固定的绝缘带电球壳处在另一个旋转的绝缘带电球壳中心，分析了该体系电磁场从建立到稳定，再到撤去的过程中，整个系统角动量的变化情况。验证了在建立稳定电磁场的过程中，外力提供的冲量矩一部分转化为电磁场角动量储存在电磁场中，一部分提供体系的转动机械角动量，当撤掉磁场后，电磁场角动量转换成机械角动量，整个过程角动量守恒。

电磁场；动量；角动量

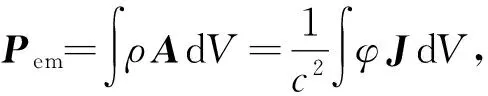
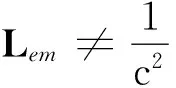
电磁场具有角动量，当撤掉电磁场后角动量如何转化？在本文中，通过一个简单的模型，分析建立和撤销稳恒电磁场的过程中角动量的转化，并讨论Lem=∫r×ρAdV的物理意义。

1 电磁场基本理论

1.1 电磁场动量

根据标准电磁场理论，电磁场动量密度为：

(1)

整个空间的电磁场动量为

(2)

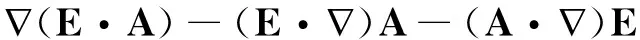
因为[8]

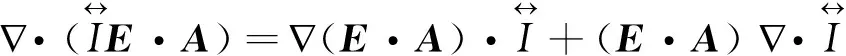
且满足

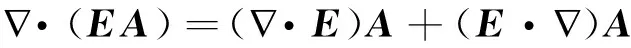
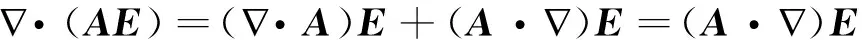
合并以上3式得：

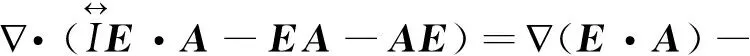
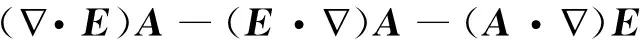
即

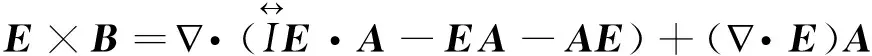
因此

(3)

上式右边第一项是曲面积分，因为在无穷远边界上没有电磁场流入和流出，所以面积分为零。因此可以得出电磁场动量的另一表达式

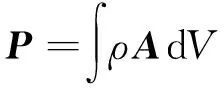
(4)

又因为对静场，

其中

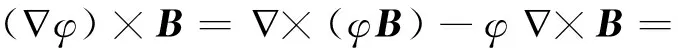
而∫vdV×(φB)=∮sdS×(φB)=0，因此又得到电磁场动量的另一个表达式

(5)

1.2 电磁场角动量

根据标准电磁理论，电磁场角动量为

(6)

与电磁场动量有3种表示对应，角动量是否也有类似3种表示形式呢？文献[7]中证明，对于轴对称分布的电磁体系，Lem=∫r×ρAdV是成立的。根据公式(6)，若用标势φ来表示电场，则有

(7)

上式最后一项一般不等于零。对于轴对称分布的情况，

(8)

上式也不等于零，可以看出，只有在球对称情况下才有-ε0∫r×[×(φB)]dV=0，所以一般情况下。即对于恒定电磁场体系，电磁场动量，轴对称分布情况下，角动量Lem=∫r×(ε0E×B)dV=。

2 固定的绝缘带电球壳处在旋转的绝缘带电球壳中心

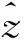
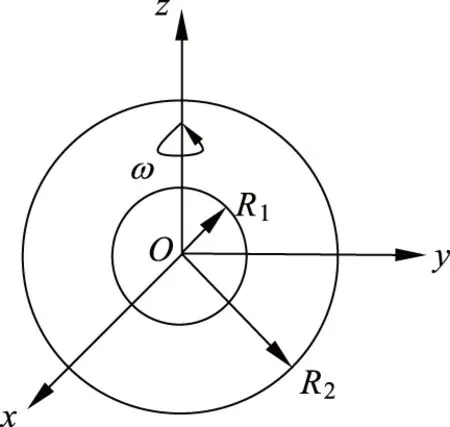
图1 带电球壳处在旋转的带电球壳中心

2.1 体系达到稳定的过程

首先考虑外球壳从静止开始转动的过程。设在外力推动下，外球壳缓慢地从静止开始转动，随着外球壳转动角速度不断增加，球壳内外的磁感应强度也在不断增加，因此会产生环绕z轴的涡旋感应电场，内外球壳都会受到感应电场力的作用，产生沿z轴方向的力矩。根据法拉第电磁感应定律，

(9)

对于r

(10)

对内球壳，在某一时刻所受的感应电场力力矩为

(11)

假设体系达到稳定状态以后，外球壳内的磁感应强度为B0，则整个过程中感应电场力对内球壳的冲量矩为

(12)

对外球壳，在转动的某一时刻所受的感应电场力力矩为：

(13)

整个过程中感应电场力对外球壳的冲量矩为

(14)

2.2 稳定体系电磁场角动量的计算

当外球壳以稳定的角速度ω转动时，计算体系的电磁场角动量。

转动的带电球壳产生的磁场的矢势为

(15)

(16)

矢势A可以有无限多种取值，这里取了库仑规范中最简单的一组解，若取其他的规范，A的表示形式会不相同，但对物理结果不会产生影响。

空间磁场分布为

(17)

(18)

其中

(19)

空间电场分布为

(20)

(21)

(22)

1) 利用Lem=ε0∫vr×(E×B)dV计算电磁场角动量

因为在rR2的范围内有电磁场角动量。

在R1

(23)

在r>R2区域，设电磁场动量密度为pout，角动量密度为lout，则：

(26)

(27)

(28)

所以，电磁场总的角动量为

(29)

显然，与第2.1节的计算结果一致。

2) 利用Lem=∫r×ρAdV计算电磁场角动量

先对内球壳进行计算：

(30)

再对外球壳进行计算：

(31)

(32)

公式(29)与(32)完全一样，这是一个柱对称的体系,说明在本系统中Lem=r×ε0∫v(E×B)dV与Lem=∫r×ρAdV两个式子是等价的。当然，r×ρ A并不能看成电磁场角动量密度，因为电磁场角动量存在于整个空间，不仅仅是有电荷分布的区域。那么为什么可以从r×ρ A出发得到电磁场角动量呢？

这个问题可以通过建立稳定电磁场体系的过程来考虑：

一般情况下电场可用矢势和标势表示为

(33)

所以感应电场力对体系的冲量矩为

(34)

对于具有柱对称的体系，∫r×(-φ)ρdtdV=0。在建立稳定电磁场的过程中,外力需要克服感应电场力做功，相应的冲量矩为-IE=∫r×ρAdV,这部分冲量矩即转化为电磁场角动量,所以，电磁场角动量可以表示为Lem=∫r×ρAdV。

2.3 球壳停止转动

当给外球壳一个反向的力矩，使其慢慢停止转动时，磁场会逐渐减小，空间会产生感应电场，与过程2.1相反，带电球壳在感应电场力的作用下受到向上的力矩。感应电场大小与公式(10)一样，方向相反。

整个过程中感应电场力对内球壳的冲量矩为

(35)

感应电场力对外球壳的冲量矩为

(36)

感应电场力对体系的总冲量矩为

(37)

球壳停止转动后，电磁场角动量消失，而公式(37)与公式(29)和(32)完全相等，即储存在电磁场中角动量全部释放出来转化成了机械角动量，要想让带电外球壳停下来，除了要克服外球壳的机械角动量Iω，还必须给外球壳一个额外的冲量矩克服冲量矩I2。对内球壳，固定轴给它提供了一个向下的冲量矩克服了向上的冲量矩I1。如果在撤掉磁场的过程中，固定内球壳的固定轴突然撤去，内球壳在I1的作用下必然会转动起来，具有向上的角动量，如果没有摩擦的话，内球最后的角动量为I1。这也是对费曼佯谬[9]的理解。

3 结语

在静电磁场体系中，存在电磁场动量和电磁场角动量，通过上面这个模型的讨论可以看出，在静电磁场中，体系总的角动量为电磁场角动量与体系转动的机械角动量之和。在建立稳定电磁场的过程中，外力的冲量矩一方面抵消感应电场力对体系的冲量矩，另一方面提供体系转动的机械角动量。其中抵消感应电场力冲量矩的部分即转化成电磁场的角动量储存在电磁场中。对具有柱对称的体系，这个冲量矩恰好可表示为L=∫r×ρAdV，与电磁场角动量L=ε0∫vr×(E×B)dV计算的结果完全一致。当撤去磁场后，电磁场角动量转换成机械角动量。

[1] Babson D, et al. Hidden momentum, field momentum, and electromagnetic impulse[J]. Am.J.Phys, 2009, 77(9): 826-833.

[2] Griffiths D J. Resource Letter EM-1: Electromagnetic Momentum[J]. Am.J.Phys, 2012, 80(1): 7-18.

[3] Shockley W, James R P. “Try simplest cases” discovery of “hidden momentum” forces on “magnetic currents”[J]. Phys.Rev.Lett, 1967,18(20): 876-879.

[4] Coleman S, Van Vleck J H. Origin of “hidden momentum forces” on magnets[J]. Phys.Rev, 1968,171(5): 1370-1375.

[5] Jaber S M A. Energy and momentum considerations in an ideal solenoid[J]. J.Electromagn.Anal.Appl, 2010, 2(03): 169-173.

[6] Mcdonald K T. Electromagnetic momentum of a capacitor in a uniform magnetic field” 《www.hep.princeton.edu/～mcdonald/examples/cap_momentum.pdf》.

[7] Gauthier N. A theorem about the angular momentum and magnetic energy of stationary,axial field distributions[J]. Am.J.Phys, 2006, 74(3): 232-235.

[8] 贾兆平，刘惠恩. Feynman圆盘佯谬与角动量守恒[J]. 大学物理,1983,2(4): 1-3. Jia Zhaoping， Liu Huien. Feynman’s disk paradox and the conservation of angular momentum[J]. College Physics, 1983, 2(4): 1-3. (in Chinese)

[9] Feynman R P, Leighton R B, Sands M. The Feynman lectures on Physics[M]. Reading MA: Addison-wesley, 1964, 2: 17-51.

■

ELECTROMAGNETIC ANGULAR MOMENTUM OF A SYSTEM WITH TWO CONCENTRIC CHARGED SPHERICAL SHELLS

Zhao Huiyuan Ruan Jianhong

(School of Physics and Materials Science, East China Normal University, Shanghai 200241)

Electromagnetic momentum and angular momentum are interesting and basic topics of classical electromagnetism. According to the basic electromagnetic theory, the angular momentumLem=ε0∫vr×(E×B)dV. For static case, it can also be expressed asLem=∫r×ρAdV, which is analyzed simply in this paper. Through a simple electromagnetic system, which contains two concentric insulated charged spherical shells with the bigger one is rotating, change of the angular momentum of the total system is discussed. We conclude that in the process of establishing a static electromagnetic field, part of the impulse moment provided by the external force is converted into the electromagnetic angular momentum which is stored in the field, and part of it is converted into the rotatingmechanical momentum of the system. When the field is removed, the electromagnetic angular momentum converts into the mechanical angular momentum, and the total angular momentum of the system is conserved.

electromagnetic field; momentum; angular momentum

2017-01-06

中国石油大学(华东)教改重点项目：大学物理数字化教学研究与实践(编号：JY-A201618)。

赵慧媛，女，硕士研究生，研究方向为电磁场理论，441771559@qq.com。

阮建红，女，教授，主要从事电磁学、电动力学教学及科研工作，研究方向为粒子物理、电磁场理论，jhruan@phy.ecnu.edu.cn。

赵慧媛，阮建红. 两个同心带电球壳体系电磁场角动量的研究[J]. 物理与工程，2017，27(5)：51-55.