用磁荷观点解释单极感应现象

赵 强 刘 萍

(西安交通大学理学院，陕西 西安 710049)

教学经验交流

用磁荷观点解释单极感应现象

赵 强 刘 萍

(西安交通大学理学院，陕西 西安 710049)

本文首先利用磁荷观点计算了旋转磁铁端面上的磁流，然后利用磁流的安培环路定理求出单极感应发电机回路中的电动势，并且指出回路中的电动势与回路的形状无关。利用磁荷观点还克服了使用相对论观点时对磁铁旋转速度过度限制、对磁铁端面磁场过度简化以及计算复杂的缺点。

磁荷观点； 单极感应现象； 电动势；磁流；对称性

贾起民先生在他的《电磁学》一书中向读者介绍了这样一个既有趣、又让人感到十分困惑的现象：“单极感应现象”[1]。为了讨论此现象，首先将贾起民先生对此现象的介绍转述如下：

单极感应现象是一种运动磁体的电磁感应现象。当一圆柱形磁体以恒定的角速度ω绕其对称轴旋转时，在与这磁体滑动接触的静止的回路中出现一稳恒的电流。这现象最早由法拉第进行了研究，后被韦伯命名为单极感应发电机(此名字并不恰当)，其示意图如图1所示。

关于单极感应现象起因的解释，历史上曾有过剧烈的争论。以法拉第为代表的观点认为：当轴对称的磁体绕其对称轴旋转时，周围空间的磁场分布并无变化，但是导电的磁体在磁场中运动。运动的导电磁体(图中的CP2)切割磁感应线，从而产生感应电动势，因此这是一种动生电动势，电动势的源分布在磁体内部。另一种观点以韦伯为代表，这种观点认为磁场的磁感应线跟随磁体一起以ω旋转，运动的磁感应线切割静止的导线回路，从而产生感应电动势。因此电动势源分布在静止不动的回路中。电动势究竟在哪里？要用实验回答这一问题是困难的。

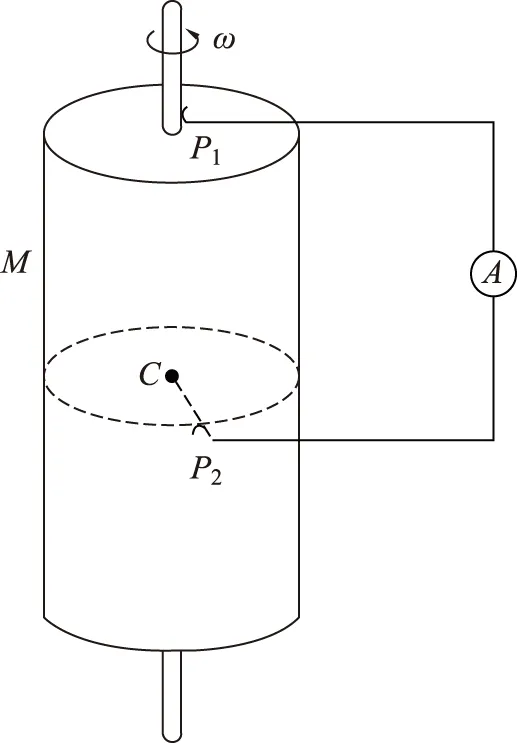
图1 单极感应发电机

法拉第认为不论磁铁是静止还是转动，其外部的磁场均保持不变这一观点虽不符合相对论对电磁场变换的观点，但在磁铁转速不大的情况下是近似正确的。但法拉第认为电动势只存在于转动的磁铁中这一观点则是错误的。韦伯认为电动势分布于静止的回路中的观点符合实际，但是他认为磁铁的磁场“刚性”连接于磁铁的观点则是不符合现代物理学对场的认识。这正如贾起民先生在他的《电磁学》中所述：“从场是独立于源的一种实体的观点看来，磁感应线跟着场源运动的说法是站不住脚的，这在前面已有所述。”[1]

贾起民先生是用狭义相对论的观点来解释单极感应现象的。但在我们看来，此种方法有3个缺点：第一是由于在计算过程中使用了电磁场的相对论变换公式，计算过程比较复杂。特别是对于初学者有相当困难；第二是为了得到整个回路电动势的具体数值，假设磁体端面上的磁场为均匀场。这一假设有些过度简化；第三是认为磁铁的转速“比较小”，将转动的磁铁近似看做惯性系。这不仅对问题的范围形成了过度限制，而且将转动系看做惯性系总让人有点“不安”。实际上为了使感应现象明显，磁铁的转速不会太小。而人们更感兴趣的是高速转动情况，这对于仅能处理惯性参考系问题的狭义相对论有很大的挑战性。这也正如贾起民先生在他的书中所说的那样：“因为单极感应问题涉及转动，在这里是否可直接应用仅适用于惯性系间相互转换的狭义相对论的结果也是值得商榷的。因而，以上讨论仅代表对单极感应现象的一种看法，对此问题有兴趣的读者可进一步查阅有关文献。”[1]为了克服以上的缺点，下面我们尝试用磁荷观点来解释单极感应现象。

我们首先假设图1中圆柱形的磁铁沿对称轴方向(指向上方)均匀磁化，其极化强度为M。根据等效的磁荷观点[2，3]，此圆柱形磁铁的磁极化强度为J =μ0M，其上端面将会出现一层面密度为σm=μ0M的均匀正磁荷。当磁铁以角速度ω绕对称轴旋转时，磁铁端面上的磁荷将形成以P1点为中心的环状磁流，如图2所示。在图2中，半径为r，宽度为dr的细圆环上的磁荷量为

dqm=2πσmrdr=2πμ0Mrdr

(1)

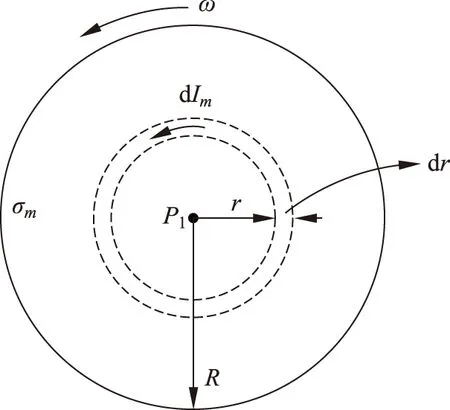
图2 磁荷观点下旋转磁铁端面的磁流

当磁铁以角速度ω旋转时，细环中的磁荷生成的磁流为

dIm=μ0Mωrdr

(2)

旋转磁铁整个端面上的环形磁流为

(3)

下面我们需要解决这样的问题：旋转磁铁端面的磁流会在空间产生什么样的效应？这效应由什么样的规律来描述？我们知道，电流会在其周围产生磁场，这磁场由安培环路定理来描述。根据磁荷与电荷之间的对称性，磁流必然会在其周围产生电场。这电场应由“磁流的安培环路定理”(也可称为“磁荷世界的安培环路定理”)来描述[4]，其具体形式为

(4)

式(4)中的右边之所以会出现负号，是因为磁流方向和回路L的绕行方向之间的关系满足“左手定则”，而我们仍然选择了“电荷世界”中的“右手定则”。式(4)的左边恰好是单极感应发电机回路中电动势的定义。将式(3)代入式(4)，有

(5)

至此，以上所有的讨论过程没有任何近似，是完全精确的。式(5)表明，在实验室参考系中来看，磁流引起的感应电动势是分布在单极感应发电机的整个回路中的。回路中电动势的数值只与穿过回路的磁流Im有关，而与回路的形状无关(这一点与贾先生认为回路中的电动势与回路的形状有关这一观点有所区别)。由式(3)可以看出，穿过回路的磁流只与磁铁的形状、磁铁的磁化强度以及磁铁的转速有关。

另外，根据相对论的观点(尽管相对论的观点不是本文的主要观点，但也不得不涉及)，只要旋转磁铁边缘的线速度远小于光速，旋转磁铁的磁场在实验室系中的分布状态和在磁铁静止的参考系中的分布状态一样。磁铁的转速ω显然满足上述条件，这是因为自然界中再“坚硬”的物体，当其由于高速转动而解体时的线速度都必然远小于光速(即使《西游记》中的“定海神针”也不例外)。因此，本文完全不对旋转磁铁的角速度ω做任何限制！既然按照相对论的观点，在实验室系中可以“看到”磁场，同时回路中的CP2段又在转动，那么CP2段除了存在磁流引起的感应电动势外，还存在由于洛伦兹力引起的感应电动势。具体计算式为

(6)

式(6)中的积分区间是从R到0的原因是因为回路L的标定方向是从P2指向C。为了将式(6)具体计算出来，我们可假设磁铁是无限长(这时有了轻微近似)，则其内部为均匀场，具体值为B=μ0M。将此值代入式(6)，有

(7)

单极感应发电机回路中总的电动势为E1与E2的和，即

(8)

综上所述，我们可以看到用磁荷观点解释单极感应现象，比用相对论观点解释单极感应现象不仅简洁、普遍、精确，而且物理图像清晰，争议性小。但由于磁荷观点考虑的是整个回路中的电动势，因此对局部回路的电动势认识不清，例如CP2段，这是其缺点(根据相对论的观点，不论是在实验室系还是转动参考系，CP2段上的电动势都为零。)

最后需要指出的是：即使像法拉第和韦伯这样伟大的物理学家也对单极感应现象有争议，因此，必然会有读者对我们的观点有所异议。我们也抱着和贾先生一样的态度：“以上的讨论仅代表对单极感应问题的一种看法”。我们诚恳希望广大读者对我们的观点批评指正！

[1] 贾起民，郑永令. 电磁学(下册)[M].上海：复旦大学出版社，1987：153-155.

[2] 钟锡华.电磁学通论[M].北京：北京大学出版社，2014：278-285.

[3] 赵凯华，陈熙谋.电磁学(下册)[M].北京：人民教育出版社，1978：94-110.

[4] 赵强.读“等效的磁荷观点”有感[J].物理与工程，2014，24(4)：20-21.ZhaoQiang.Impressionafterreadtheviewpointof“equivalentmagneticcharge”[J].PhysicsandEngineering, 2014， 24(4)： 20-21. (inChinese)

■

EXPLAINING THE MONOPOLE INDUCTION PHENOMENON WITH THE MAGNETIC CHARGE VIEWPOINT

Zhao Qiang Liu Ping

(School of Science, Xi’an Jiaotong University, Xi’an Shaanxi 710049)

In this paper, the magnetic current on the end face of the rotating magnet is calculated by using the viewpoint of magnetic charge. The electromotive force in the loop of a monopole induction generator is obtained by using Ampere’s loop law of magnetic current, which pointed out that the electromotive force in the circuit is not related to the shape of the circuit. Using the viewpoint of magnetic charge, we also overcome the disadvantages in the method of using the relative theory, including the excessive restriction of the magnet’s rotating speed, the excessive simplification of magnet field at the end face of magnet, and the complex computation.

viewpoint of magnetic charge; monopole induction phenomenon; electromotive force; magnetic current; symmetry

2016-05-25

赵强,刘萍. 用磁荷观点解释单极感应现象[J]. 物理与工程，2017，27(5)：44-46.