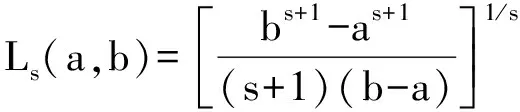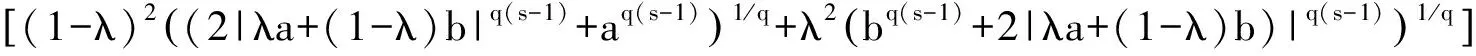关于(α,m)凸函数的几个积分不等式及其应用
2017-09-12尹红萍
双 叶,尹红萍
(内蒙古民族大学 数学学院,内蒙古 通辽 028043)
关于(α,m)凸函数的几个积分不等式及其应用
双 叶,尹红萍
(内蒙古民族大学 数学学院,内蒙古 通辽 028043)
研究了(α,m)-凸函数的一些性质,并利用Hölder不等式得到了一些新的(α,m)-凸函数的Hermite-Hadamard型不等式,最后给出了这些不等式在特殊平均值中的应用.
(α,m)-凸函数;Hermite-Hadamard型不等式;Hölder不等式
凸函数的研究非常活跃,并且它的研究具有重要的理论意义,它的应用也非常广泛.本文研究了(α,m)-凸函数的Hermite-Hadamard型不等,得到了几个结果,并给出特殊平均值中的应用.首先介绍一些与之相关的基本知识和基本概念.
设f∶I⊆R→R是定义在I上的凸函数.a,b∈I,a (1) 下面引入凸函数的定义: 定义1[1]设f∶I⊆R→R是I上的函数,若对任意的x,y∈I,λ∈[0,1],不等式: f(λx+(1-λ)y)≤λf(x)+(1-λ)f(y), (2) 成立,则称f是I上的凸函数. 1985年G.Toader首先提出了m凸函数的定义. 定义2[2]设f∶[0,b]→R(b>0),m∈(0,1],若对任意的x,y∈(0,b],λ∈[0,1],有: f(λx+m(1-λ)y)≤λf(x)+m(1-λ)f(y), (3) 则称f(x)为[0,b]上的m-凸函数. 1993年,V.G.Mihesan给出了(α,m)-凸函数的定义. 定义3[3]设f∶[0,b]→R(b>0),(α,m∈(0,1]2,若对任意的x,y∈(0,b],λ∈[0,1],有: f(λx+m(1-λ)y)≤λαf(x)+m(1-λα)f(y) (4) 则称f(x)为[0,b]上的(α,m)凸函数. 文献[4-9]得到了上面凸函数的相关定理. 定理1[4]设f∶I∘⊂R→R为I∘上的可微映射,a,b∈I∘,a (5) 定理2[5]设f∶I→R为I上的可微函数,f′∈L[a,b],0≤a (6) 定理3[6]设f∶I→R为I上的可微函数,f′∈L[a,b],0≤a (7) 为了证明定理需要下面的引理. 引理1[7]设f∶I⊂R→R是I∘上的可微映射,a,b∈I且a 现在建立几个(α,m)-凸函数的Hermite-Hadamard型不等式. 证毕. 推论1 在定理4的条件下,若时α=m=1,则有下面不等式成立: 证明 由引理1和Hölder不等式,有: 和 因此有: 证毕. 推论2 在定理5的条件下,若α=m=1时,则有下面不等式成立: 证明 由引理1和Hölder不等式,有: 因此,有: 证毕. 推论3 在定理6的条件下,若q=1时,则有下面不等式成立: 推论4 在定理6的条件下,若α=m=1时,则有下面不等式成立: 推论5 在定理6的条件下,若α=m=q=1时,则有下面不等式成立: 下面利用第2节的结果给出(α,m)-凸函数的Hermite-Hadamard型不等式在特殊平均值中的一些应用. 设b>a>0,定义加权平均和广义平均值分别为: 令f(x)=xs,x>0,s>1,q≥1且q(s-1)≥1,则有:|f′(x)|q=sxq(s-1)是(0,∞)上的凸函数. 由推论2,有: 定理7 设b>a>0,s>1,q>1,q(s-1)≥1,λ∈[0,1],则: 由推论3,有: 定理8 设b>a>0,s>1,q≥1,q(s-1)≥1,λ∈[0,1],则: 此外若s≥2时,则有: [1]MITRINOVICDS,PEˇCARI′C,FINKAM.ClassicalandNewInequalitiesinAnalysis[M].Dordrecht:KluwerAcademic,1993. [2] TOADER G.Some Generalizations of the Convexity [J].Proceedings of Colloquium on Approximation and Optimization,Univ Cluj-Napoca,1985:329-338. [3] MIHESAN V G.A generalization of the converity,Seminar on Functional Equations,Approx,Convex[M].Romania:Cluj-Napoca,1993. [4] DRAGOMIR S S,AGARWAL R P.Two inequalities for differentiable mappings and applications to Special means of real numbers and to trapezoidal formula[J].Appl Math Lett,1998,11:91-95. [5] BAKULA M K,ÖZDEMIR M E,PEˇCARI′C J F.Hadamard type inequalities for m-convex and -convex functions[J].J Inequal Pure Appl Math,9(2008),no.4,Article 96,12 pages;Available online at http://www.emis.de/journals/JIPAM/article1032.html. [7] CHEN Feixiang,FENG Yuming.New Inequalities of Hermite-Hadamard Type for Functions Whose First Derivatives Apsolute values are s-convex [J].Italian Journal of Pure and Applied Mathematics-N,2014,32:213-222. 责任编辑:时 凌 Some Integral Inequalities of (α,m)-Convex Function and the Application SHUANG Ye,YIN Hongping (College of Mathematics,Inner Mongolia University for Nationalities,Tongliao 028043,China) The paper studied some properties of (α,m)-convex function,and got some new Hermite-Hadamard inequalities of (α,m)-convex function by the Hölder inequality.Finally,the applications of the inequalities on the particular mean were given. (α,m)-convex function; Hermite-Hadamard inequalities; Hölder inequality 2017-04-17. 内蒙古自治区高等学校科学研究项目(NJZY16185). 双叶(1974-),女(蒙古族),硕士,副教授,主要从事凸分析理论的研究. 1008-8423(2017)03-0292-05 10.13501/j.cnki.42-1569/n.2017.09.011 O A




1 有关引理
2 (α,m)-凸函数的Hermite-Hadamard型不等式






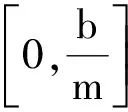


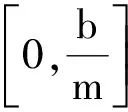
3 特殊平均值的应用