基于随机车流的大跨径双层公路悬索桥疲劳性能评估*

刘沐宇 韩 征 邓晓光

(武汉理工大学道路桥梁与结构工程湖北省重点实验室 武汉 430070)

基于随机车流的大跨径双层公路悬索桥疲劳性能评估*

刘沐宇 韩 征 邓晓光

(武汉理工大学道路桥梁与结构工程湖北省重点实验室 武汉 430070)

由于车辆荷载在桥梁上的分布状态极为复杂，在进行疲劳性能评估时，采用标准疲劳车进行加载不能真实反映杆件的受力历程.采用蒙特卡罗法模拟各个车道的随机车流作为疲劳荷载，将其加载到危险杆件的应力影响线上，得到更加符合实际情况的应力时程.随后采用雨流计数法处理应力时程得到危险杆件的应力谱，根据等效损伤累计理论计算危险杆件200万次的等效应力幅用以疲劳性能评估.结果表明，武汉杨泗港长江大桥钢桁梁疲劳性能满足设计要求.

疲劳性能评估；随机车流；双层公路桥；钢桁梁；等效应力幅

0 引 言

桥梁在进行疲劳性能评估时，疲劳荷载的选取直接影响着评估结果.20世纪70年代，英国制定了用于钢桥抗疲劳设计的车辆荷载谱，美国、欧洲等国随后也开展了这方面的研究工作，并制定了相应的疲劳规范[1].童乐为等[2]开始对公路城市桥梁荷载谱进行研究，将车辆按照车型、车重和轴距等方面对标准车辆进行定义，弥补了国内在标准车辆荷载方面的空白.但是由于各地交通状况不尽相同，单一的车辆荷载谱不能完全适用.近年来，国内学者针对这种情况提出由实测车流简化得到模型车辆[3].周泳涛等[4]通过实地的交通车辆调查，确定了通行车辆的荷载形式，依据疲劳累积损伤原理推导出各省适用的模型车辆.然而在实际运营阶段，车辆荷载是随着时间不断变化的，桥梁杆件的受力状况必然十分复杂，采用模型车辆无法真实反映实际交通荷载状况[5].陈惟珍等[6]提出基于交通量统计的虚拟车流作为疲劳荷载，用于钢桥的疲劳评估.随机车流方法能够考虑实际车辆荷载特征，如车型、车重、车距及日交通量等，可应用于桥梁结构应力谱的提取及疲劳性能评估中[7-8].通过模拟桥梁上的车流作为疲劳荷载，基于等效损伤累积理论和疲劳细节分类研究桥梁的疲劳性能[9]，得到更加精确的评估结果.

文中在确定了杨四港长江大桥车流参数的基础上，采用Monte-Carlo方法模拟各个车道的随机车流作为疲劳荷载，再进行影响线加载得到危险杆件的应力时程，进行雨流计数法得到应力谱.根据等效损伤累计理论计算危险杆件200万次的等效应力幅用以疲劳性能评估，评估结果为武汉杨泗港长江大桥疲劳设计提供参考.

1 基于随机车流的桥梁疲劳性能评估

1.1 随机车流模拟方法

通过随机车流的模拟可以更真实地反映作用在桥梁上的实际车辆，为钢结构桥梁的疲劳分析提供有力的依据，因此模拟随机车流成为一项重要的工作.

由于Monte-Carlo方法可以很好地模拟随机性问题，故采用这种方法来产生随机车流，使其具有与实际车流特性相同的分布特征[12]，具体步骤为：①根据车型比例参数，采用均匀分布随机数产生相应的车型编号；②根据车距参数，采用对数正态分布随机数得到前后车间距；③根据各车型相对应的车重参数，采用对数正态分布随机数得到随机车重值；④将以上各数值形成单车道交通荷载随机数组.

结合MATLAB软件编制程序来模拟随机车流，抽样函数见表1.

表1 MATLAB软件的随机抽样函数

其中，MU=lg (M2/sqrt(V2+M2))，SIGMA=sqrt(lg (V2/M2+ 1))；M、V分别为数据的均值和标准差.

在随机车流的模拟过程中作如下假定：①假定所有车道具有相同的车型比例，这样增加了不同车道之间重车相遇的概率，应当是偏安全的；②假定各车道随机车流是独立的，不考虑车辆换道的情况；③在疲劳计算过程中车速的快慢主要影响一次循环完成所需要的时间，而对于构件应力循环的大小和次数的影响可以忽略，所以假定车辆匀速前进，不发生加速或减速[13].

为了确定车流参数，将所有车辆划分为若干类型，然后根据相关文献得到特定车型对应的车重均值和标准差.按照英国规范BS5400中的相关规定进行各车道车流量划分计算得到各车道车流量，再根据车速确定车距的均值和标准差.

将车流量、车型、车重、车距的参数输入程序，便可以得到某一时间段的随机车流数据，然后输出所需表格、图形.

1.2 基于随机车流的桥梁疲劳性能评估

基于随机车流的疲劳性能评估方法主要是通过数值模拟得到随机车流作为疲劳荷载，然后基于线性累积损伤准则和疲劳细节分类进行评估.

首先建立桥梁有限元模型，选取《公路钢结构桥梁设计规范》疲劳荷载计算模型=在桥梁双层的最外侧车道进行加载，做移动荷载分析.疲劳荷载计算模型Ⅰ采用等效的车道荷载，集中荷载为0.7Pk，均布荷载为0.3qk.Pk和qk按公路-Ⅰ级车道荷载标准取值.通过比较杆件应力幅值的大小，确定各个部位的危险杆件.然后从有限元模型中分别提取各个车道在危险杆件1/2截面处的应力影响线.

将随机车流荷载作为间距不变的一系列集中力加载到相应车道在危险杆件1/2截面处的应力影响线上，即σk=∑pi·yi，得到一个车道荷载作用下的应力大小σk.然后将所用车道荷载作用下的应力相叠加得到某一时刻的应力状态，即στ=∑σk.由于模拟的随机车流长度远大于桥长，所以以1 m为步长把随机车流荷载的位置沿着影响线的方向向前移动，并重新进行加载计算，可以获得危险杆件的应力时程.根据英国BS5400规范的规定，小于30 kN的所有车辆均忽略不计.

利用雨流计数法处理危险杆件的应力时程，得到不同应力水平的循环次数，即疲劳应力谱.然后根据等效损伤累计理论计算危险杆件的等效应力幅[14]，即

式中：Δσ为循环200万次时等效应力幅；KF为调整系数； ΔNi为应力幅值；ni为与ΔNi对应的结构在设计寿命期内循环次数.

将其与危险杆件疲劳细节分类的容许应力幅进行对比，评估钢桁梁在全寿命期内的疲劳性能[15].具体评估流程见图1.

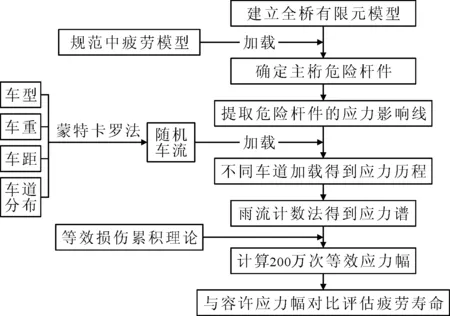
图1 疲劳性能评估方法

目前国内外规范中的疲劳荷载均没有给出双层公路桥的适用条件，并且大跨径双层公路桥的车辆分布状态复杂，所以考虑通过模拟随机车流得到危险杆件的应力时程用于双层公路桥的疲劳性能评估，为桥梁疲劳评估提供了可行途径.

2 工程应用

2.1 工程概述

武汉杨泗港长江大桥总长约4.3 km，是武汉第一座双层公路悬索桥，上层双向6车道，为城市快速路；下层双向4车道，并设非机动车道，为城市主干路.杨泗港长江大桥采取一跨跨越长江的方案，跨度达1 700 m，钢桁架主梁，混凝土桥门架塔，是世界上跨度第二大的悬索桥.主桥总体布置见图2，横断面布置见图3.大桥主梁为华伦式钢桁架，材料为Q345Qd，桁高10 m，两片主桁架中心间距28 m，标准节间长9 m.上、下弦杆和斜腹杆均选用箱形截面，竖腹杆选用H形截面.斜腹杆、竖腹杆和弦杆通过整体节点板连接.钢桁架构造见图4.

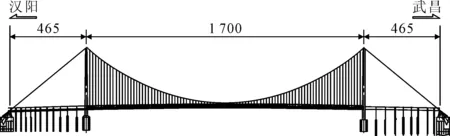
图2 主桥总体布置图(单位：m)

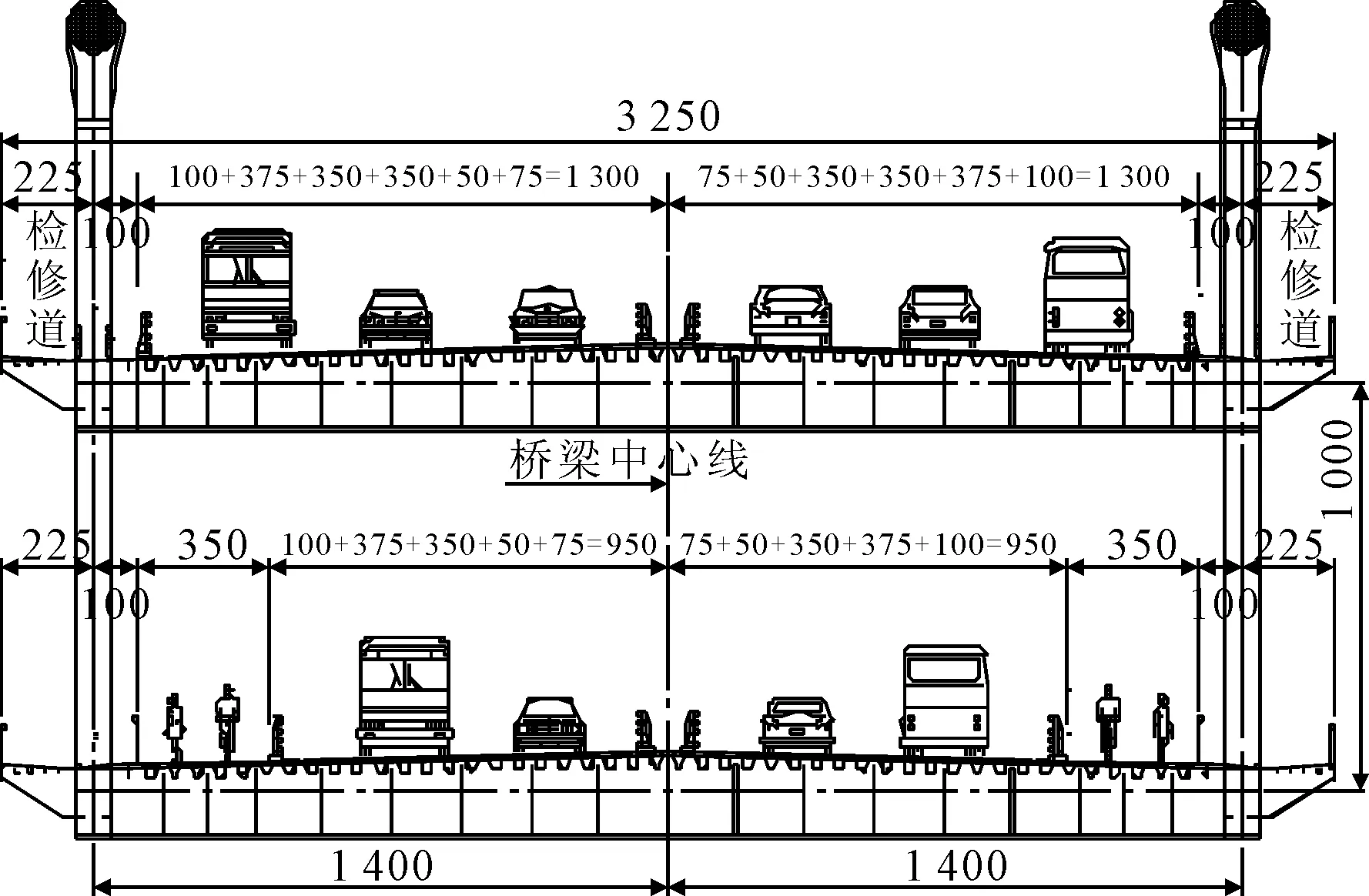
图3 杨泗港长江大桥横断面布置图(单位：cm)

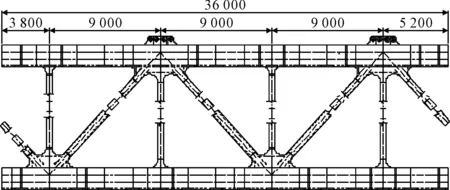
图4 钢桁架构造示意图(单位：mm)

2.2 有限元模型建立

采用MIDAS/Civil建立杨泗港长江大桥全桥有限元模型，主桁杆件(包括上弦杆、下弦杆、竖腹杆和斜腹杆)采用梁单元，主缆和吊杆采用只受拉单元，吊杆和主梁的连接采用共用节点的方式，全桥共建立8 796个单元，其中8 418个梁单元， 378个只受拉单元.各部位材料特性及单元类型见表2，全桥有限元模型见图5.

表2 材料特性及单元类型

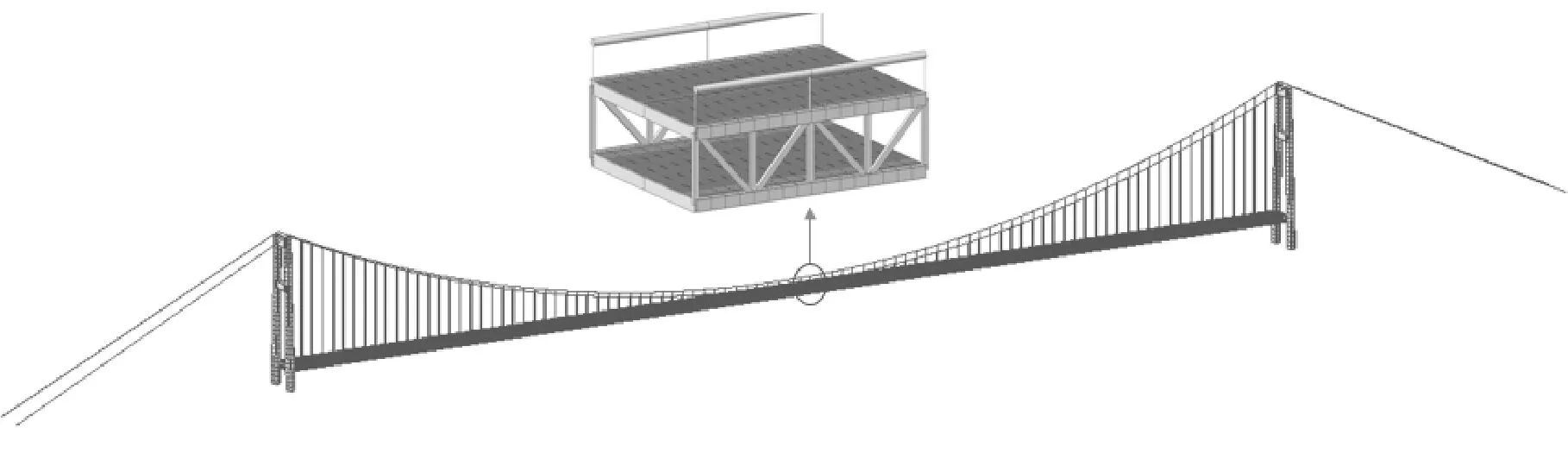
图5 杨泗港长江大桥有限元模型

选取疲劳荷载计算模型Ⅰ在桥梁双层的单向最外侧车道同时进行加载，根据移动荷载分析的结果，通过比较分别找出上弦杆、下弦杆、竖腹杆和斜腹杆的应力幅值最大的杆件单元，见表3.

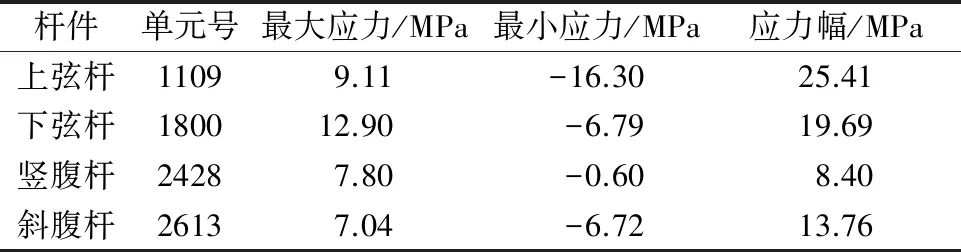
表3 主桁杆件最不利位置及应力幅

上弦杆最危险单元为1109号单元，距离跨中646.875 m.下弦杆最危险单元为1800号单元，距离跨中43.875 m.竖腹杆最危险单元为2428号单元，距离跨中738 m.斜腹杆最危险单元为2613号单元，距离跨中778.5 m.

2.3 随机车流模拟

武汉市交通发展战略研究院制定的《杨泗港大桥工可阶段交通流量预测分析》指出，2038年(建成运行20年)大桥全日车流量为11.3万辆/d，上下层通行车流的比例为59∶41.综合考虑杨泗港大桥的区位及功能定位，确定其白天(05:00-19:00)与夜间(19:00-05:00)通行车流的比例为75∶25.

把所有车辆划分为5类代表性车型，包括出租车、小客车、大客车、小货车、大货车，编号分别为1～5，车型比例见表4.

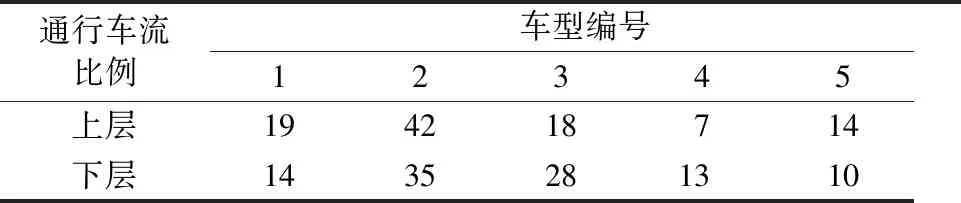
表4 车型比例 %

考虑到杨泗港大桥为新建桥梁，此处的车重均值和标准差根据车型参考文献[10]中的调查数据，见表5.

表5 车重参数

车道分布按照英国规范BS5400中上层慢车道和邻车道比例为2∶1.5，下层慢车道和邻车道比例为1.5∶1进行计算，各车道车流量见表6.

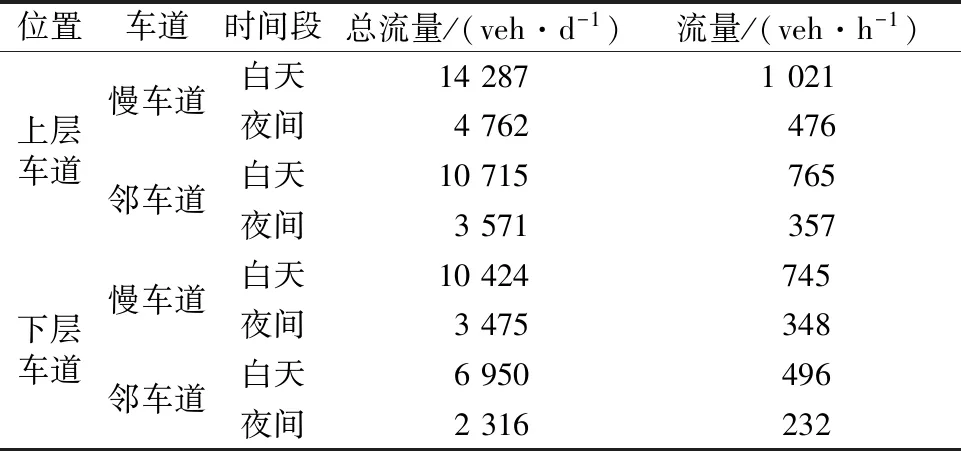
表6 各车道车流量

本文假设所有车辆以15 m/s的速度匀速前进，计算得到杨泗港长江大桥各车道的平均车距，见表7.

表7 车距参数

在模拟过程中，根据车速及车距均值确定车距标准差取10.

把以上得到的车流量、车型、车重和车距的参数输入程序进行模拟.考虑数据的容量，分别模拟各个车道白天1 h和夜间1 h的随机车流.以上层慢车道白天1 h的模拟结果为例，数据形式见表8.

表8 上层慢车道白天1 h随机车流

在MATLAB平台，生成的某一时刻桥长范围内车型、车重和位置见图6.

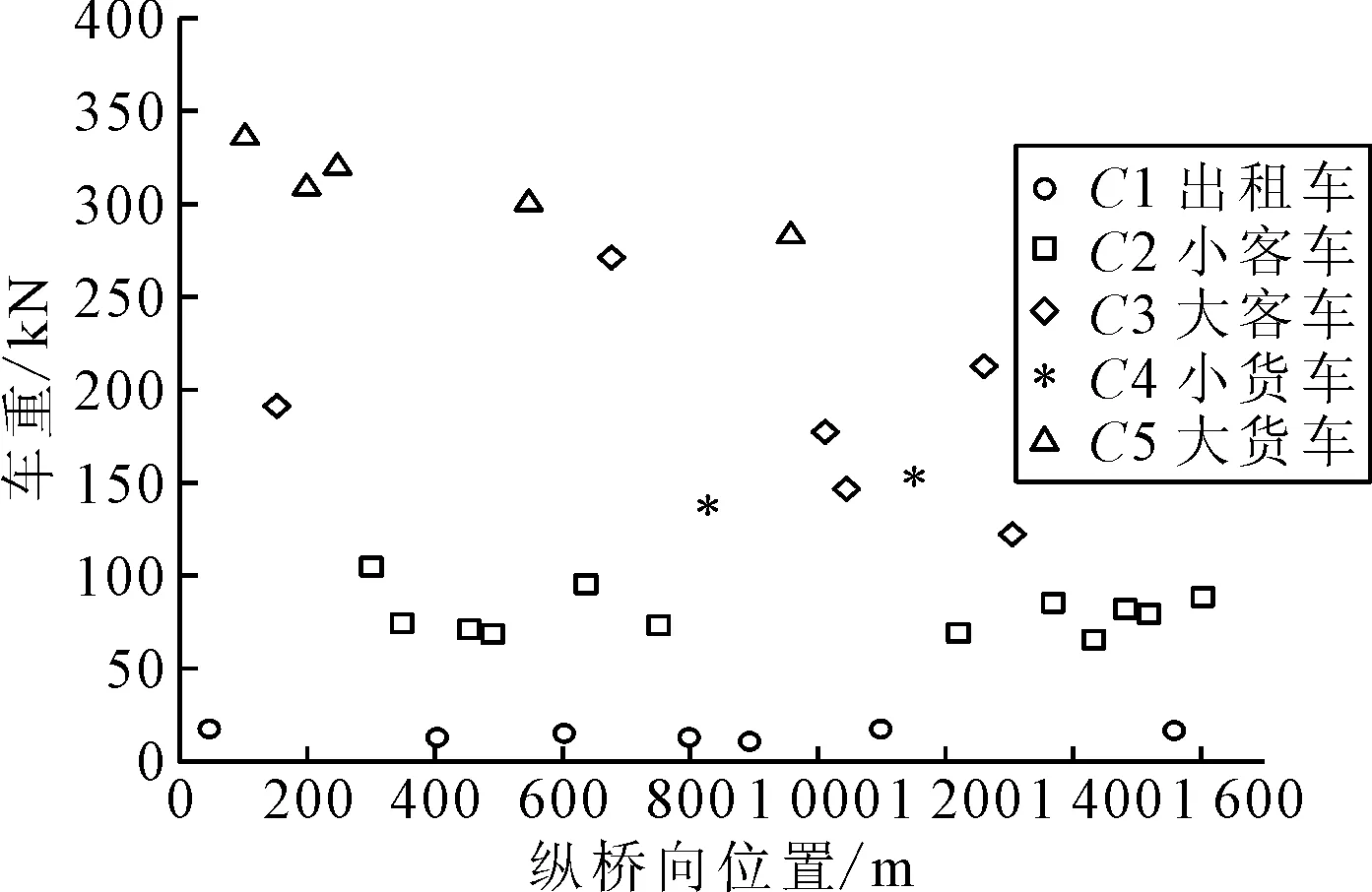
图6 某一时刻桥上随机车流

2.4 危险杆件应力谱

从有限元模型中提取各个车道在危险杆件1/2截面处的应力影响线.由于篇幅限制，仅展示上层慢车道在斜腹杆2613单元处的应力影响线，见图7.

图7 斜腹杆2613单元应力影响线

利用MATLAB软件编制影响线加载程序，把各个车道的随机车流荷载加载到相应的影响线上，根据σk=∑pi·yi和στ=∑σk得到某一时刻危险杆件的应力大小στ，见图8.

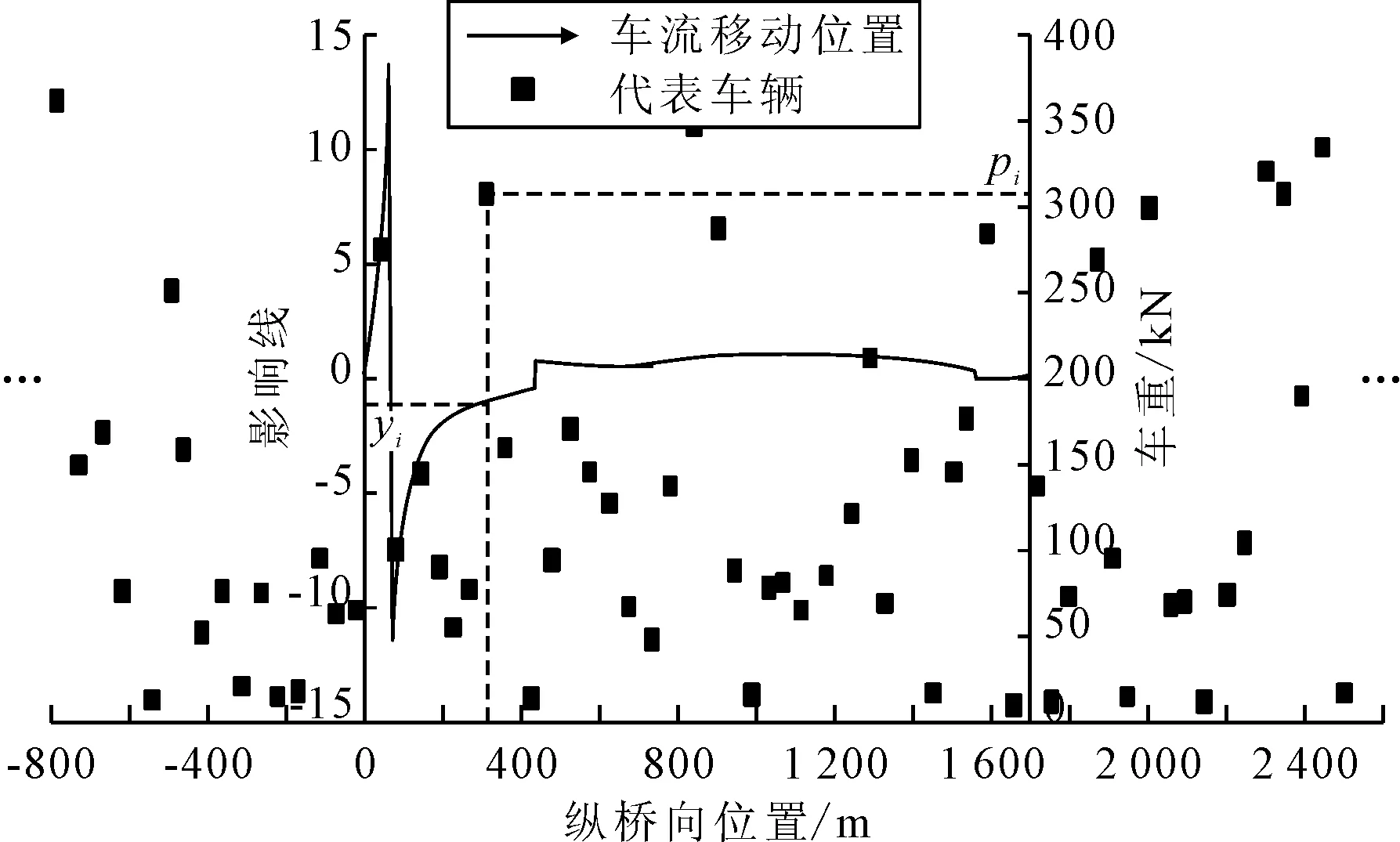
图8 t时刻影响线加载示意图

将随机车流以1 m为步长沿着影响线的方向向前移动，并重新进行加载计算得到下一时刻危险杆件的应力大小στ+1.由于车速为15 m/s，所以可以得到危险杆件间间隔为1/15 s的应力时程.由于篇幅限制，仅展示斜腹杆2613单元白天1 h的应力时程，见图9.

图9 斜腹杆2613单元白天1 h应力时程

根据雨流计数法的特点，利用MATLAB软件编制程序快速实现，主要步骤为：①去除等值点以及非峰谷值点；②用“4点法”遍历应力-时间历程序列提取载荷循环，见图10，直至剩余所有点组成发散波；③对发散波进行半循环计数；④对前面得到的循环进行计数，得到每个应力水平的循环次数.

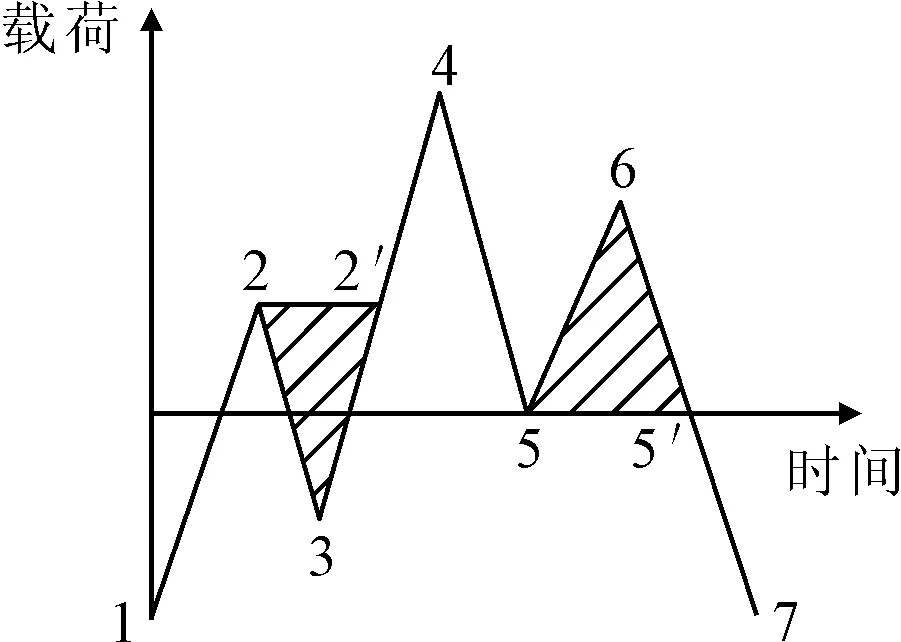
图10 “4点法”提取循环荷载

分别处理各个危险杆件的应力时程，按照白天14 h、夜间10 h计算得到危险杆件1 d的应力谱，见表9.

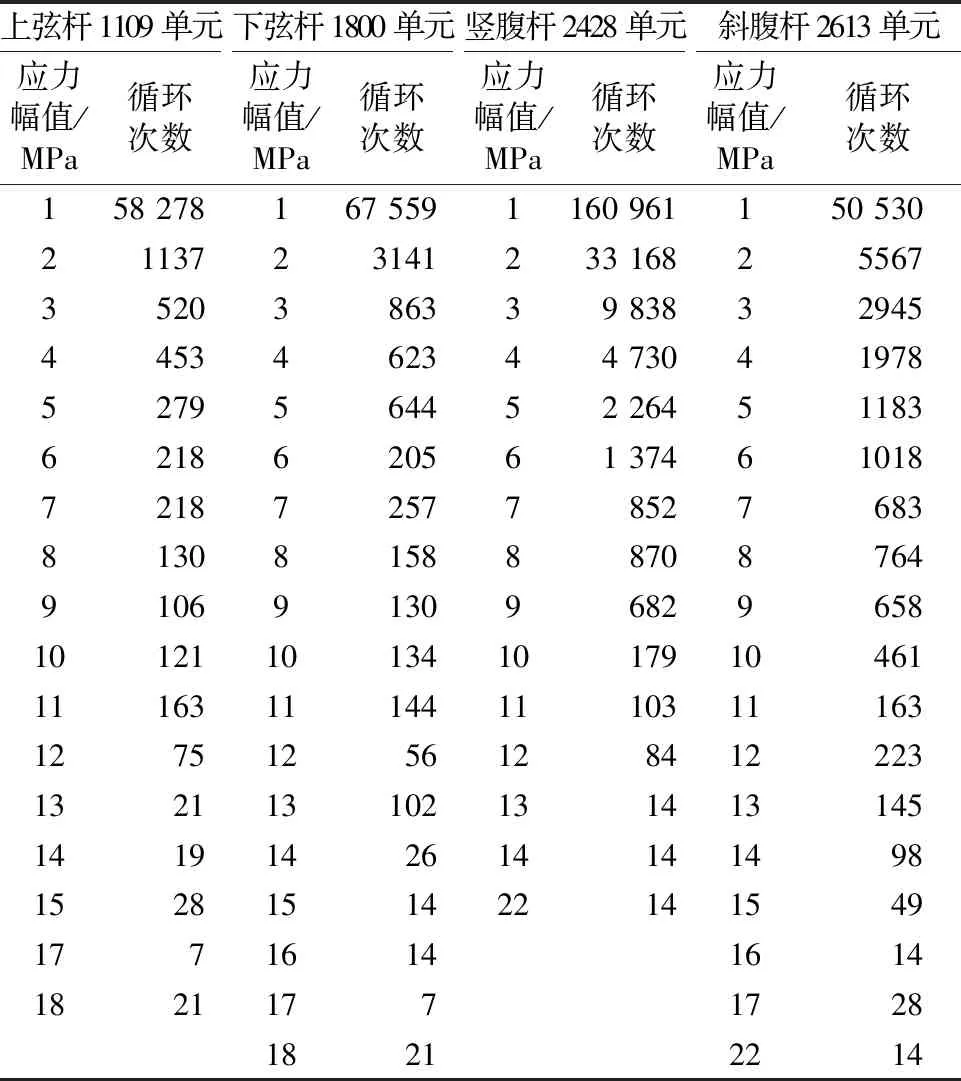
表9 各危险杆件应力谱

2.5 疲劳性能评估结果

根据英国BS5400规范，当采用车辆荷载频值谱法计算损伤度时不计入KF，即取KF=1.根据各危险杆件一天的应力谱，代入式(1)计算在全寿命期100年内的等效应力幅，结果见表10.

表10 各危险杆件等效应力幅 MPa

杨泗港长江大桥采用全焊钢桁梁结构，上、下弦杆和斜腹杆均选用箱形截面，竖腹杆选用H形截面.根据我国《公路钢结构桥梁设计规范》中关于疲劳细节的分类，焊接箱形截面疲劳细节类别为100 MPa，焊接H形截面疲劳细节类别为110 MPa.

由此可见，上弦杆、下弦杆、竖腹杆和斜腹杆的等效应力幅都小于容许应力幅，即杨泗港长江大桥钢桁梁疲劳性能良好，在全寿命期内疲劳性能满足设计要求.

3 结 论

1) 在杨泗港大桥工可阶段交通流量预测分析报告以及英国疲劳规范BS5400的基础上确定交通荷载参数，给出了基于随机车流的钢桁梁疲劳性能评估方法.不同于规范中的疲劳荷载，随机车流更具有针对性，可以适用于不同地区的桥梁疲劳性能评估.

2) 利用《公路钢结构桥梁设计规范》疲劳荷载计算模型Ⅰ确定了杨泗港长江大桥钢桁梁疲劳破坏危险杆件，分别为：距离跨中646.875 m处的上弦杆，距离跨中43.875 m处的下弦杆，距离跨中738 m处的竖腹杆，距离跨中778.5 m处的斜腹杆.

3) 经计算，杨泗港长江大桥危险杆件等效应力幅最大值出现在斜腹杆处，大小为41.56 MPa，小于规范限值，说明钢桁梁在全寿命期内的疲劳性能满足设计要求.

[1]刘沐宇,罗航.武汉二七长江三塔结合梁斜拉桥疲劳特性分析[J].武汉理工大学学报(交通科学与工程版),2014(6):1193-1197.

[2]童乐为,沈祖炎,陈忠延.城市道路桥梁的疲劳荷载谱[J].土木工程学报,1997(5):20-27.

[3]王荣辉,池春,陈庆中,等.广州市高架桥疲劳荷载车辆模型研究[J].华南理工大学学报(自然科学版),2004(12):94-96.

[4]周泳涛,鲍卫刚,翟辉,等.公路钢桥疲劳设计荷载标准研究[J].土木工程学报,2010(11):79-85.

[5]CHOTICKAI P, BOWMAN M D. Truck models for improved fatigue life predictions of steel bridges[J]. Journal of Bridge Engineering,2006,11(1):71-80.

[6]陈惟珍,王春生,徐磊.上海市外白渡桥剩余寿命与使用安全[J].桥梁建设,2002(2):6-10.

[7]王涛,韩万水,黄平明.公路桥梁交通荷载研究现状及展望[J].建筑科学与工程学报,2010(4):31-38.

[8]王春生,陈艾荣,陈惟珍.铆接钢桥剩余寿命与使用安全评估实例[J].同济大学学报(自然科学版),2006(4):461-466.

[9]咸庆军,童乐为.型钢混凝土梁疲劳特性研究[J].华中科技大学学报(自然科学版),2016,44(4):90-94.

[10]邵雨虹,吕彭民.九江长江大桥疲劳车辆荷载谱[J].长安大学学报(自然科学版),2015,35(5):50-56.

[11]鲁乃唯,刘扬,邓扬.随机车流作用下悬索桥钢桥面板疲劳损伤与寿命评估[J].中南大学学报(自然科学版),2015(11):4300-4306.

[12]程高,刘永健,张俊光,等.基于Monte Carlo法的多车道公路桥梁车流模拟[J].重庆交通大学学报(自然科学版),2011,30(6):1375-1378.

[13]刘兴,王辉,方兴.公路钢桥疲劳设计荷载的研究分析[J].北方工业大学学报,2012(3):78-83.

[14]孙晓燕,徐冲,王海龙,等.用于疲劳可靠性分析的公路桥梁荷载效应研究[J].公路交通科技,2011(5):80-85.

[15]刘高,吴文明,唐亮,等.坝陵河大桥钢桁加劲梁主桁架整体节点疲劳试验[J].土木工程学报,2009(12):142-148.

Fatigue Performance of 1 700 m-span Double Deck Suspension Bridge Based on Random Traffic Flow

LIU Muyu HAN Zheng DENG Xiaoguang

(HubeikeylaboratoryofRoadwayBridgeandStructureEngineering,WuhanUniversityofTechnology,Wuhan430070,China)

Since the distribution of the vehicle load on the bridge is very complex, using standard fatigue car loading cannot truly reflect the force of the rod in the fatigue assessment. In this paper, Monte Carlo method is used to simulate the random traffic flow in each lane as a fatigue load, which will be loaded into the stress influence line of the dangerous bar to get a more realistic stress time history. Then the stress spectrum of the dangerous rod is obtained by the rain flow counting method, and the equivalent stress amplitude is calculated by the equivalent damage cumulative theory to evaluate the fatigue performance of the 2 million times. The results show that the Wuhan Yangsigang Yangtze River bridge steel truss beam fatigue performance meet the design requirements.

fatigue performance evaluation; random traffic flow; double deck highway bridge; steel truss girder; equivalent stress amplitude

2016-12-20

*国家自然科学基金项目(51378405)、中国工程院重点咨询研究项目(2016-XZ-13)资助

U441+.4

10.3963/j.issn.2095-3844.2017.04.008

刘沐宇(1963—)：男，博士，教授，博士生导师，主要研究领域为桥梁工程