塔身腹杆非常规布局的力学特性及设计方法研究

2020-12-30

建筑机械化 2020年12期

（沈阳建筑大学机械工程学院，辽宁沈阳 110168）

一般情况下塔机正方形截面塔身4 片桁架的腹杆的布局都是相同的，常用的腹杆布局形式有W 型、N 型和K 型3 种形式，如图1 所示。在国内外已经有了许多关于这些塔身腹杆受力状态的研究。对于腹杆的布局一般有两个目的：①要承受塔身的水平力和上部质量在回转和在风载作用下产生的扭矩；②改善主肢的稳定特性。

图1 塔身腹杆常用布局形式

现在国外有一些塔机生产厂商的塔身四片采用不同的腹杆布局形式，如图2 所示的是利勃海尔公司生产的塔机，其塔身腹杆一面是K 形桁架，其余三面是N 型桁架或W 型桁架。可以将这两种塔身腹杆结构称之为K3N 和K3W。对于这样的布局目前国内外尚未见到相关的设计理论，也未见到对其有关特点的研究。本文针对这类非常规腹杆布局进行特性分析，并提出相应的设计方法和设计理论。

图2 塔身非常规腹杆布局

1 非常规塔身腹杆力学特性分析

如图2 所示为非常规腹杆布局，是1 片塔身桁架为K 型桁架，而另外2 片是常规形式。固定式上回转塔机在工作时经常受到的水平载荷有风载荷、变幅惯性力和回转惯性力。一般情况下，塔身顶部只受到水平载荷时，塔身会沿着载荷方向发生水平位移。但在塔身腹杆不一致时，由于K 型腹杆片在相同水平力作用下，产生的位移就可能与其它片产生的水平位移不一致，这种不一致就会导致塔身上部出现一定量值的扭转角度与小量值侧向位移。图3 是K3W 腹杆布局加载及变形示意图。图3a 是两平行于K 片桁架的剪力作用于塔顶上的示意图，图3b 是塔顶在平行剪力作用下有限元模型变形效果图。图4 是K3N 腹杆布局。这两种腹杆布局在相同的加载状态下，顶部端面相对于底部截面都有扭转角，也有一定量的侧向位移，是由于K 片与其平行片的刚度差造成的。

图3 K3W平行剪力加载端面变形俯视图

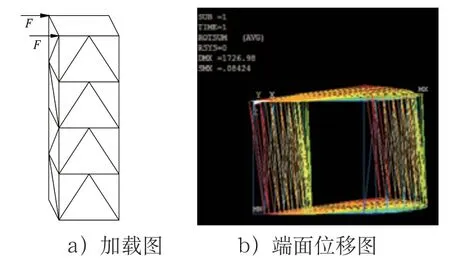
图4 K3N平行剪力加载端面变形俯视图

K3N 和K3W 两种腹杆布局的塔身在纯扭矩的作用下，上端面在发生扭转的同时，也产生小量值水平位移，图5 和图6 给出了两种结构产生的位移变化。形成水平位移也是由于K 片桁架的平面内刚度与其它片不相同产生的结果。这种附加的水平位移会在轴力的作用下产生附加二次应力，为塔身的强度带来不利影响。

图5 K3N纯扭矩作用俯视变形图

图6 K3W纯扭矩作用俯视变形图

2 非常规腹杆布局塔身等刚度设计方法

为了解决腹杆异形布局所带来的不利影响，在设计上应力求K 型桁架平面内的刚度与其它桁架在平面内的刚度相等，这样可以保证其变形与其它桁架片具有一致协调性，使之不会产生附加扭转角与侧向位移。下面以经典力学为基础，对K 型桁架与N 型桁架和W 型桁架所形成的平面内刚度相等的设计方法进行研究。

图7 给出了一种K 型桁架，两种N 型桁架，即N1 型和N2 型两种，和W 型桁架结构形式。N1 型桁架的横腹杆是受力的，横腹杆承受水平载荷，N2 型桁架的横腹杆不受力，横腹杆是零杆。对于横腹杆是零杆的N2 型桁架，其腹杆的受力状态与W 型相同。下面首先研究N1 型横腹杆承受水平力的结构形式。

图7 四种腹杆形式简图

对于图7a 和图7b 两种形式，在水平力作用点都产生水平位移，其腹杆和弦杆都影响桁架平面内的位移，但两者弦杆相同，对桁架水平位移的影响也相同，在以水平位移相等为目标的研究中可以忽略弦杆对位移的影响。对于图7a 和图7b 的计算模型可以简化为图8a 和图8b，对一个节间的位移模型进行研究。

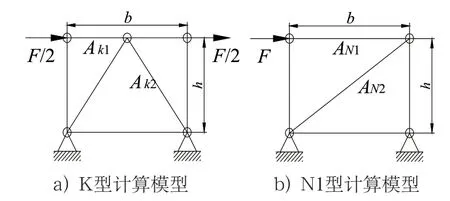
图8 计算简图

依据虚功原理可以求得K 型桁架一个节间在载荷作用点的位移为

设Ak2=γAk1，则上式（1）可改写为

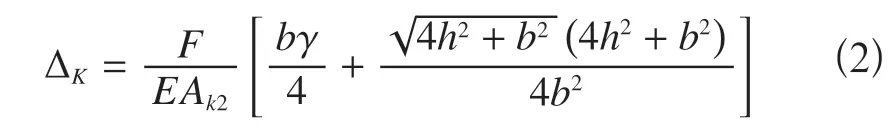
式中γ为K 型桁架的斜腹杆截面积Ak2与水平腹杆截面积Ak1之比γ=Ak2/Ak1。

N1 型桁架在载荷作用点的位移为

设AN2=ηAN1，则式（3）可改写成

式中η为N 型桁架的斜腹杆截面积AN2与水平腹杆截面积AN1之比η=AN2/AN1。

对于N2 型和W 型与N1 的不同就在于横腹杆不受力或没有横腹杆。这样N2 型和W 型的水平位移可以统一用W 型表达，且斜腹杆的截面积用N替代式（4）中的AN2，则位移表达式可写成

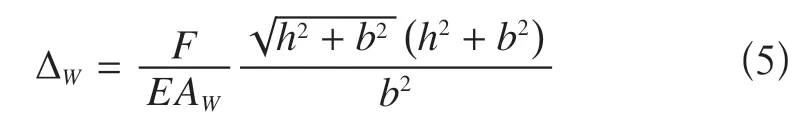
为了研究方便，将N2 型和W 型都记为W进行研究。则ΔN2W用ΔW进行表示。为了使K型与N1 型和W 型的水平刚度相同，则可令：ΔK=ΔN1和ΔK=ΔW，分别求得K 型桁架腹杆参数与N1 型和W 型桁架腹杆参数的对应关系。

当ΔK=ΔN1，且用替代Ak2，可得

当ΔK=ΔW时，且用替代Ak2，可得

一般情况下，斜腹杆的布局有两种情况，一种是横腹杆与斜腹杆的截面相同，另一种是横腹杆与斜腹杆受力状态相等。

对于横腹杆与斜腹杆的截面相同的状态，可取γ=1，η=1 根据式（6）可得K 型腹杆横截面与N1 型腹杆横截面等刚度的条件为

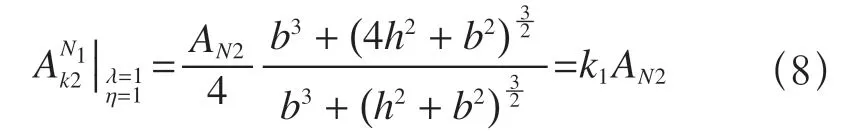
式中k1是与AN2的面积比例系数

根据式（7）可得K 型腹杆横截面与W 型腹杆截面等刚度的条件为

式中k2是与AW的面积比例系数

对于斜腹杆与水平腹杆受力相等的状态，可用腹杆的轴力值相等求得γ值为

η值为

将式（10）和式（11）代入式（6）可得K 型腹杆横截面与N1 型腹杆横截面等刚度的条件为

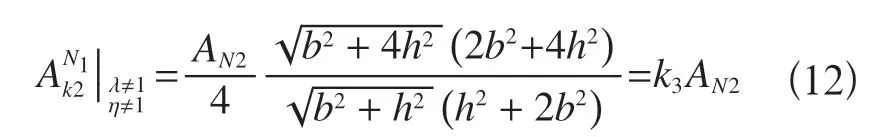
式中k3是与AN2的面积比例系数

将式（10）代入式（7）可得K 型腹杆截面与W型腹杆截面等刚度的条件为

式中k4是与AW的面积比例系数

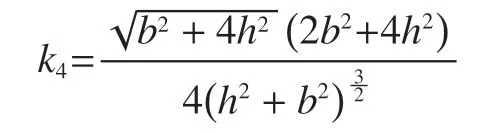
3 腹杆截面积比例关系分析

以一款6015 塔机为例，其塔身标准节的轴线宽度b=1665mm，单节间长度h=1400mm，其中一片采用K 型桁架，其余三片均采用文中前面提到讨论的N 型和W 型桁架，斜腹杆截面积为AN2=AW=1435mm2。依据式（8）、式（9）、式（12）和式（13）依次可得

上述数据显示，当N 型桁架有横腹杆，且横腹杆承受水平力时，由于累计变形量增加，降低了水平位移刚度，使得比例系数k1和k3减小，降低了K 型桁架斜腹杆的截面积。而对于横腹杆不受力或没有横腹杆的W 型桁架，只有斜腹杆参与水平位移，提升了水平位移刚度，使得比例系数k2和k4都增大，使得K 型桁架斜腹杆的截面积也随之增加。

从式（8）、式（9）、式（12）和式（13）可以发现，k1～k4都是b和h函数，当b和h发生变化时k1～k4四个系数也将同时发生变化，则Ak2也随之变化。