平面图的非正常染色*

张传妮, 王应前

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

平面图的非正常染色*

张传妮, 王应前

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

研究了特殊平面图的非正常染色问题.应用经典的权转移方法,证明了4-圈不与3-,4-圈相邻且不含7-圈的平面图是(1,1,0)-可染的.这一结果进一步拓展了平面图的非正常可染的充分条件.

平面图;圈;权转移;非正常染色

0 引 言

自从四色猜想成为四色定理[1-2](每个平面图是4色可染的)之后,Steinberg猜想[3](每个既没有4-圈又没有5-圈的平面图是3色可染的)便成为图染色理论中的一个焦点.为解决这一具极强挑战性的猜想,许多学者[4-6]作出了诸多努力,并在多方面推广了图的经典染色.图的非正常染色(或缺陷染色)便是推广之一.更准确地说,设d1,d2,…,dk是k个非负整数,G=(V,E)是一个图,若可以用k个色,譬如,c1,c2,…,ck,去染G的顶点,使得每个染色ci的顶点至多有di个邻点染有同样的色(i=1,2,…,k),则称G是非正常(d1,d2,…,dk)-可染的,简称为(d1,d2,…,dk)-可染的.运用这一术语,四色定理可改述为“每个平面图是(0,0,0,0)-可染的”,Steinberg猜想可改述为“每个既没有4-圈又没有5-圈的平面图是(0,0,0)-可染的”.图的非正常染色已得到广泛研究,并已得到许多有趣的结果.例如:

每个平面图是(2,2,2)-可染的[7];

每个既不含5-圈又不含相邻三角形的平面图是(1,1,1)-可染的[8].

从非正常染色角度研究Steinberg猜想所取得的最好结果可总结为下面的定理:

定理1 每个既没有4-圈又没有5-圈的平面图是:

1)(列表)(1,1,1)-可染的[4];

2)(3,0,0)-可染的[5];

3)(1,1,0)-可染的[9-10];

4)(2,0,0)-可染的[6].

由于Vincent Cohen-Addad等[11]最近证明了Steinberg猜想是错误的,因此提出如下更一般的猜想就显得更有研究意义.

推广的Steinberg猜想:对于l∈{6,7,8,9},既不含4-圈又不含l-圈的平面图是(0,0,0)-可染的.

同样,从非正常的角度研究此猜想所取得的最好结果,以及对最好结果作出的进一步改进,可总结为下面的定理:

定理2 每个既没有4-圈又没有l-圈的平面图是:

1)(3,0,0)-和(1,1,0)-可染的[12];(2,0,0)-可染的[13],其中l=6;

2)(2,0,0)-可染的[14]和(1,1,0)-可染的[15],其中l=7;

3)(1,1,0)-可染的[15],其中l=8;

4)4-圈不与3-圈相邻且不含6-圈的平面图是(1,1,0)-可染的[16].

鉴于不含6-圈的平面图可推出4-面不与4-面相邻的结论,为此本文将证明如下结果:

定理3 4-圈不与3-,4-圈相邻且不含7-圈的平面图是(1,1,0)-可染的.

1 一些术语和记号

设图G是有限、简单、无向图.一个平面图是指一个可平面图在平面内的一个嵌入.对于平面图G,用V,E,F和δ分别表示平面图G的顶点集、边集、面集和最小度.对任意的一个顶点v∈V,用d(v)表示v在G中的度数,即与v关联的边的条数.若d(v)=k(d(v)≥k或d(v)≤k),则称v是一个k-点(k+-点或k--点).称边xy∈E为(d(x),d(y))-边,且x是y的d(x)-邻点.对于一个面f∈F,用d(f)表示f的边界的长度,称为面f的长度.上述有关点的概念对于面或圈同样适用.若v1,v2,…,vk是f上按某一时针方向连续出现的点,则记f=[v1,v2,…,vk],且称f为一个(d(v1),d(v2),…,d(vk))-面.3-圈又称为三角形.若一个点(或一条边)与一个三角形相关联,则称该点(或该边)是三角的.若uv∈E,且uv是非三角的,则称u是v的一个孤立邻点,否则是非孤立邻点.若一个3-点v关联一个3-面f,则称v的不与3-面相关联的那个邻点v′为v或f的外d(v′)-邻点,且称f是v′的一个悬挂3-面.若点v恰关联k个不相邻的三角形,则称v是k-三角的.若2个圈(或2个面)至少共用一条边(点),则称这2个圈(或2个面)相邻(相交).

若一个4-点v关联1个(4,4,4)-面且有2个孤立3-邻点,则称v是轻的,记为4l-点.

若一个4-点v关联1个 (3,4,5+)-面且有2个孤立3-邻点,则称v是弱的,记为4w-点;

若一个5-点v关联1个(3,4,5)-面和1个(3,4w,5)-面,则称v是1-坏的,记为5b-点.

若一个5-点v关联1个(3,5,5+)-面和1个(3,4w,5)-面且有1个孤立3-点,则称v是2-坏的,记为5bb-点.

2 定理3的证明

假设定理3不真.设G=(V,E,F)为定理3的一个顶点最少的反例,也就是说G本身不是(1,1,0)-可染图,但G的任意一个正常的点导出子图G′有一个(1,1,0)-染色φ,则G有以下结构性质：

引理1[9-10]1)δ(G)≥3;

2)G中的3-点至多有1个3-邻点;

3)若3-面f=[uvw]中d(u)=d(v)=3,则d(w)≥5;

4)若3-点v关联1个(3,4,4)-面,则v的外邻点是4+-点;

5)4-点至少有1个4+-邻点;

6)关联1个(3,4,4)-面的1-三角4-点至少有1个孤立4+-邻点;

7)关联1个(3,4,4)-面的2-三角4-点的另一个3-面不是(4,4-,4-)-面.

引理2[15]若5-点v关联2个3-面T1=[v1v2v]和T2=[v3v4v]且第5个邻点为v5,则

1)T1,T2中至少有1个不是(3,3,5)-面;

2)若d(v5)=3,则T1,T2中至少有1个不是(3,4-,5)-面;

3)若T1是(3,3,5)-面,T2是(3,4,5)-面且d(v3)=3,则v3的外邻点是4+-点;

4)若T1,T2均是(3,4,5)-面且d(v1)=d(v2)=3,则v1和v3的外邻点至少有1个是4+-点;

5)T1,T2中至少有1个不是(3,4w,5)-面;

6)若T1是(3,3,5)-面,则T2不是(3,4w,5)-面;

7)若T1是(3,4,5)-面且d(v1)=3,T2是(3,4w,5)-面,则v1的外邻点是4+-点.

引理3[15]1)G中无(4l,4l,4)-面.

2)G中无(3,5bb,5bb)-面.

3)①G中4--圈不与4--圈相邻,3-面不与6-面相邻且4-面不与5-面相邻(即4-面必与6+-面相邻);

②若3-点v关联3个3-面f1,f2和f3且d(f1)=3,d(f2)=5,则d(f3)≥8;

③G中5-面至多与1个3-面相邻.

3 权转移

为完成定理3的证明,下面将运用权转移方法导出矛盾.

先假设定理3的关于点数极小的一个反例G=(V,E,F)是2-连通的,即G中每个面的边界是一个圈,G中每个点v关联d(v)个不同的面.定义初始权为ch(x)=d(x)-4,∀x∈V∪F.

设最终权函数为ch′(x).若能定义适当的权转移规则,重新分配点和面的权,使得对任意的x∈V∪F,有ch′(x)≥0,进而有

从而得到矛盾.这就证明了当G是2-连通时,定理3成立.

若一个4-点v关联1个(3,4,4)-面和3个5-面且有1个孤立3-邻点(根据引理1中的6)知,v至多有1个孤立3-邻点),则称v是坏的,记为4b-点.

根据4b-点的定义及G无7-圈,易得G无(3,4b,4b)-面.

权转移规则定义如下:

R1:5+-面转出的权:

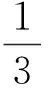
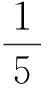
R2:转给3-点v的权:

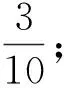
R2.2:设v不关联3-面,则v先根据R1从它关联的3个面得权,再平均地从它的4+-邻点得权,使得 ch′(v)=0.

R3:转给3-面 f=[v1v2v3]的权(其中d(v1)≤d(v2)≤d(v3)):

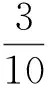
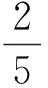
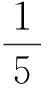
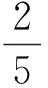
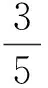
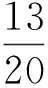
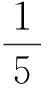
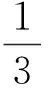
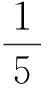
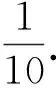
现在检验∀x∈V∪F的新权ch′(x)≥0.

先检验面的最终权.注意到d(f)≠7.

当d(f)≥8时,由R1.1知,

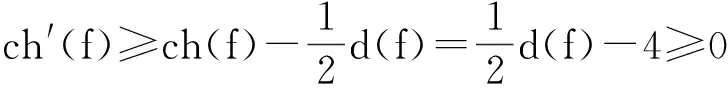
当d(f)=6时,由R1.2知,

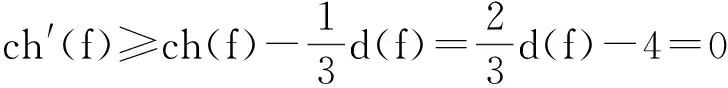
当d(f)=5时,由R1.3知,

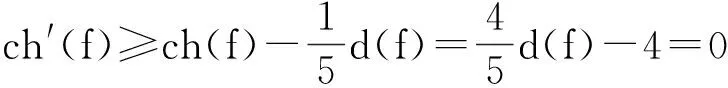
当d(f)=4时, f的权无转移,故ch′(f)=ch(f).

当d(f)=3时,设 f=[v1v2v3]且d(v1)≤d(v2)≤d(v3).由引理1中的1)知,d(v1)≥3.

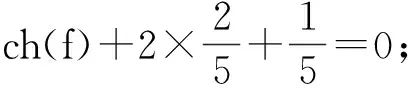
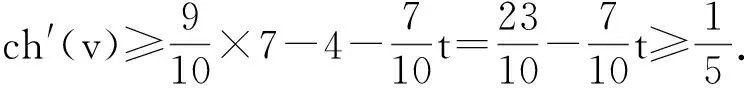
[1]Appel K,Haken W.Every planar map is four colorable,I:Discharging[J].Illinois J Math,1977,21(3):429-490.

[2]Appel K,Haken W,Koch J.Every planar map is four colorable,II:Reducibility[J].Illinois J Math,1977,21(3):491-567.

[3]Steinberg R.The state of the three color problem[J].Ann Diserete Math,1993,55(8):211-248.

[4]Lih K,Song Z,Wang W,et al.A note on list improper coloring planar graphs[J].Appl Math Lett,2001,14(3):269-273.

[5]Hill O,Smith D,Wang Yingqian,et al.Planar graphs without cycles of length 4 or 5 are (3,0,0)-colorable[J].Discrete Math,2013,313(20):2312-2317.

[6]Chen M,Wang Y,Liu P,et al.Planar graphs without cycles of length 4 or 5 are (2,0,0)-colorable[J].Discrete Math,2016,339(2):886-905.

[7]Cowen L J,Cowen R H,Woodall D R.Defective colorings of graphs in surfaces:Partitions into subgraphs of bounded valency[J].J Graph Theory,1986,10(2):187-195.

[8]Xu Baogang.On (3,1)*-coloring of plane graphs[J].SIAM J Discrete Math,2009,23(1):205-220.

[9]Xu Lingji,Miao Zhengke,Wang Yingqian.Planar graphs with cycles of length neither 4 nor 5 are (1,1,0)-colorable[J].J Comb Optim,2014,28(4):774-786.

[10]Hill O,Yu Gexin.A relaxation of Steinberg′s conjecture[J].SIAM J Discrete Math,2013,27(1):584-596.

[11]Cohen-Addad V,Hebdige M,Krl D,et al.Steinberg′s conjecture is false[J].J Combin Theory Ser B,2016,122:452-456.

[12]徐灵姬,王应前.既不含4-圈又不含6-圈的平面图的非正常染色[J].中国科学:A辑 数学,2013,43(1):15-24.

[13]Wang Yingqian,Xu Jinghan.Planar graphs with cycles of length neither 4 nor 6 are (2,0,0)-colorable[J].Inform Process Lett,2013,113(18):659-663.

[14]Liu Peipei,Wang Yingqian.Planar graphs without cycles of length 4 or 7 are (2,0,0)-colorable (in Chinese)[J].Sci Sin Math,2014,44(11):1153-1164.

[15]Wang Yingqian,Xu Jinghan.Improper colorability of planar graphs without prescribed short cycles[J].Discrete Math,2014,322:5-14.

[16]Bai Ying,Li Xiangwen,Yu Gexin.Every planar graph without 3-cycles adjacent to 4-cycles and without 6-cycles is (1,1,0)-colorable[J].J Comb Optim,2017,33(4):1354-1364.

(责任编辑 陶立方)

A note on improper colorability of planar graphs

ZHANG Chuanni, WANG Yingqian

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China)

The problem of special planar graphs of improper colorability was studied. By the discharging, it was showed that every planar graph without 4-cycles adjacent to 3-cycles or 4-cycles and without 7-cycles was (1,1,0)-colorable.The result generalized the sufficient condition for the planar graphs of improper colorability.

planar graph; cycles; discharging; improper colorability

10.16218/j.issn.1001-5051.2017.03.004

�2016-06-16；

2016-10-17

国家自然科学基金资助项目(11271335)

张传妮(1988-),女，山东临沂人，硕士研究生.研究方向：运筹学与控制论.>

O157.5

A

1001-5051(2017)03-0267-08