创新要素的流动为何如此重要？——基于全要素生产率的视角

王 钺，刘秉镰

(南开大学 城市与区域经济研究所，天津 300071)

创新要素的流动为何如此重要？
——基于全要素生产率的视角

王 钺，刘秉镰

(南开大学 城市与区域经济研究所，天津 300071)

本文旨在揭示创新要素在区际间的流动对中国全要素生产率的影响。在深入分析创新要素流动影响生产率增长内在机理的基础上，采用空间计量分析技术，对中国大陆30个省级行政区的创新要素流动与全要素生产率之间的关系进行了实证检验。研究发现，中国区域全要素生产率具有明显的空间相关效应，且受这一效应的作用，研发资本在区际间的流动对区域全要素生产率有显著的正向影响。在考虑不同引力模型下的创新要素流动量以后，这一结果依然具有稳健性。本文结论为我国创新要素区际流动政策的科学制定，进而促进全要素生产率的增长提供有益参考。

创新要素流动；全要素生产率；空间面板计量

一、引言

创新要素(主要包括R&D人员和R&D资本等)是保障创新型国家战略顺利实施，支撑中国科技竞争力提升的重要战略资源。近年来，伴随着户籍制度的松动以及互联网金融技术的迅猛发展，创新要素在区际间的流动规模逐步扩大。创新要素的区际流动有利于优化创新资源在区域空间的合理配置，加速区域创新合作网络的形成，进而也有利于推动社会技术的进步和生产率的提升。然而，创新要素的流动并非只有积极的影响，比如，在长期内，创新要素的大规模流动会使人们就业保障感和获取稳定收益的安全感显著降低[1]，而适度的就业保障感和获益稳定感对生产率增长有正向的贡献[2]。那么，创新要素在区际间的流动究竟会对我国生产率的增长产生怎样的影响呢？该问题的解决有益于我国创新要素区际流动政策和区域创新发展政策的进一步优化，并为我国创新驱动战略的成功实施提供有益参考。

从已有文献来看，目前学界尚缺乏针对创新要素流动的直接研究。现有研究均将创新要素本身作为考察对象，从静态的角度，重点考察我国创新要素的利用效率[3-5]以及创新要素的投入数量对创新绩效的影响[6-8]等。事实上，携带着更多创新知识和技术的创新要素在市场信号指引下的自由流动，会给我国经济的发展带来新的契机与挑战。因此，本文聚焦于创新要素的区际流动这一新的问题，主要考察其是否促进了我国生产率的提升。以期通过本研究，为创新要素的合理流动，从而促进创新资源的优化配置以及生产率的增长提供理论依据和政策参考。

目前关于创新要素与生产率关系的研究，大多集中于产业层面，考察各产业创新要素投入对生产率的影响。张海洋(2005)实证考察了中国内资工业部门的R&D投入与生产率的关系，结果表明R&D投入对内资部门生产率的增长有负向影响[9]；吴延兵(2006)针对我国制造业的研究表明，我国制造业的R&D投入能够显著地促进生产率的增长[10]；朱有为和徐康宁(2007)运用1996-2004年中国高技术产业的面板数据，实证检验了R&D资本积累与高技术产业生产率增长之间的关系，发现R&D资本积累对生产率有显著的影响[11]；戴魁早(2011)从行业层面对我国高技术产业的研究结果表明，不仅R&D资本投入能够促进生产率的增长，R&D人员投入也能够促进生产率的增长[12]。可以发现，上述研究忽视了创新要素在区际间流动所引发的资源配置效应的变化，而且仅以某个特定的产业作为研究对象。然而，正如上文所指出的，创新要素的区际流动对区域生产率可能产生一些有利和不利影响。在此情形下，科学分析创新要素流动影响生产率的机理，评估其影响效应，就成为研究中一项非常重要的课题。

与以往研究相比，本文的贡献主要体现在：第一，从创新要素在区际间动态流动的视角，考察中国区域生产率的提升问题，藉此为中国创新要素的合理流动及生产率的提升提供政策启示；第二，在探讨区域间生产率可能存在空间相关性的基础上，实证分析创新要素的区际流动对区域生产率的影响效应。

本文后续的安排为：第二部分从理论上阐释创新要素区际流动对区域创新生产率的影响机理；第三部分阐述创新要素流动量的度量以及区域生产率的测算方法；第四部分构建空间面板计量模型并对相关变量进行说明；第五部分对实证结果进行分析和讨论；最后给出结论及相应的政策建议。

二、理论机理

Färe等(1994)的研究表明，生产率的增长可以分解为技术的进步和技术效率的提升[13]。其中，技术进步表示生产前沿面随时间的变化向外扩张，而技术效率则表示在既定的要素投入下实际产出量与最优产出量之间的距离，距离越小，表明技术效率越高。通常新知识的创造和新发明的产生可以推动社会技术的进步，而管理机制的创新和制度的变革则能够带动技术效率的提升。作为创新生产重要投入的创新要素具有“知识性”、“技术性”和“趋利性”等特征，这些特征的存在使得其在区际间的流动一方面可以加速新知识的发明和创造，从而推动技术的进步，另一方面能够促进新的生产模式出现，助推创新执行单位技术效率的提升。这样，创新要素的区际流动便可通过促进技术进步与技术效率改善两条路径，提升区域的生产率水平。下面就这两条路径做具体分析。

创新要素流动促进技术进步的作用路径可以分为以下两个方面：第一，创新要素在区际间的流动会加速各区域的创新执行部门进行研发合作，形成研发合作网络，而异质性创新主体间的相互合作、相互互动将直接影响区域生产率的提升[14]。当前，我国技术的发展呈现出复杂化和更新速度快速化的特征，从而使得单个创新执行单位在研发过程中有可能不完全具备所需的创新知识，而跨区际的研发合作可以有效地推动创新资源的整合与创造，大大提升科学有效的整合资源、获取知识的能力，推动技术的进步。此外，在目前我国各区域依靠比较优势，对创新知识进行精细化、专门化分工的创新环境下，如何将分散的创新知识统一化、系统化，以便更加科学系统地将创新知识应用到研发中，已经成为影响区域技术进步的关键，而创新要素的流动有助于解决上述问题[15]。创新要素在区际间的流动可以将不同的异质性创新主体联合起来，形成一个相互作用、相互合作的创新网络，加快区域间的互动与合作，从而促进创新活动的顺利开展，引致技术进步。第二，创新要素在区际间的流动能够带动创新知识在区域间扩散与传播。Romer(1990)指出，创新知识的非竞争性和部分排他性特征是产生知识溢出的根本原因[16]。基于创新知识根植于创新要素的特征，创新要素在区际间的流动是引发知识溢出，特别是隐性知识溢出的主要渠道，其一方面加速了新知识的创造，另一方面又促进了创新知识在不同区域间的传播与交流，冲破了技术性创新知识中不能被编码化的部分在扩散中遇到的瓶颈问题，加快了技术进步的步伐[17]，进而有利于提高区域生产率。

创新要素流动促进技术效率改善的作用机制也主要沿以下两种路径进行：第一，在“趋利性”特征的支配下，创新要素会按照边际收益等于边际成本的原则自发地流向获益最高的地区，这种在市场规律作用下的自由流动，可以使整个社会的研发资源达到最优的配置，进而带动全社会生产率的提高。当面临技术进步的情况时，上述资源优化配置效应将表现得尤为明显。技术进步的存在，一方面，能够提高各研发部门的劳动生产率；另一方面，技术进步会影响实际收入水平，在需求收入弹性的作用下，消费者会改变对原有的研发产品的需求量。事实上，上述两种因素对不同类型的研发部门的影响存在着显著的差异，将会导致研发创新部门中失业和空缺同时存在，而创新要素的自由流动可以有效化解上述困境，实现创新知识、技术与经济发展间的最优匹配[18]，从而使创新活动有序进行，技术效率得到提升。第二，对于创新要素的流入地区，由于新流入的创新要素往往包含有较高的创新水平和管理技术，能够助推原有R&D资本形成新的、效率更高的资本，从而有利于提高创新要素的边际生产率，同时新流入的R&D资本与R&D人员相结合，可以通过学习效应提升R&D人员的边际生产率；对于创新要素的流出地区，创新要素流出后，剩余创新要素的边际生产率得到提高，同时其它要素会向边际生产率提高的部门转移，进而有利于新R&D资本的创造和R&D人员潜力的发挥。可见，创新要素的流动使得流入地和流出地创新要素的边际生产率均得到提高，从而提升区域技术效率。

三、创新要素流动量的度量及生产率的测算

本文选取创新要素中处于主体地位的R&D人员和R&D资本的流动数量来表征目前我国创新要素在区际间的流动情况。

(一)引力模型

为了得到稳定、连续的创新要素流动数据，本文借鉴白俊红和蒋伏心(2015)的做法，采用引力模型对我国创新要素在区际间的流动数量进行度量[19]。引力模型是物理学中的引力法则在社会科学中的成功运用，主要用于研究经济社会中的空间相互作用问题，其核心观点为两个经济体间的单项要素流动量与它们各自的经济发展水平成正比，与经济体间的距离成反比。早在19世纪，英国人口统计学家雷文茨坦就率先将引力模型用于人口流动的分析之中， 之后Anderson(1979)、Bergstrand(1985)、Anderson和Wincoop(2003)等经济学者分别从柯布道格拉斯支出系统法、一般均衡分析方法，多边阻力法等不同的视角，探究了引力模型的微观理论基础，使其具备了相应的微观理论支撑[20-22]。目前，引力模型已经被广泛应用于跨国贸易量度量、人口迁移以及国际投资等领域，逐渐成为研究要素流动的一个主流模型。

要素流动量引力模型的一般表达式为：

(1)

式(1)中，Mij为区域i流动到区域j的要素数量；K为区域i和区域j之间的引力系数，一般取1；Ni和Nj分别是i地和j地的某种经济变量的测度；α为引力参数，一般均取1；Rij为区域i和区域j之间的距离；b为距离衰减指数，一般取2。

参照上述引力模型的一般形式，本文在充分考虑R&D人员流动和R&D资本流动不同特征的基础上，分别构建了测算R&D人员流动量和R&D资本流动量的引力模型。

1.度量R&D人员流动量(FP)的引力模型

在实践中，由于度量主体的具体特性存在差异，为了得到最优的度量结果，经济学家根据度量主体的不同特征，对引力模型的一般形式做了恰当的变化。变化后的引力模型主要有：双对数引力模型、包含吸引力变量的产出约束引力模型等。一般认为“推拉理论”能够较好地解释人员的流动，其核心观点认为，人口迁移发生的原因在于，流入地的那些使得人员效用提高的拉力因素，以及流出地的那些对人员造成不利影响的推力因素作用的结果[23]。基于此，本文在度量R&D人员的流动量时，选用包含吸引力变量的引力模型，其中用各省区就业人员的平均工资水平来表征本省对其它省份R&D人员的吸引力，相应的引力模型如式(2)所示：

(2)

上式中，FPij为从i省流动到j省的R&D人员流动量，pei为i省的R&D人员全时当量，wagej是j省的平均工资，表征j省对i省R&D人员的吸引力，Rij是两地区省会城市之间的距离，该距离根据国家地理信息系统网站上1∶400万的电子地图用Geoda095i软件测量得到。

i省的R&D人员流入到其它所有省份的总流动量FPi，可以由式(3)求得：

(3)

上式中FPi为i省流动到其他省份的R&D人员总量，n为区域的个数，本文中n=30。

2.度量R&D资本流动量(FC)的引力模型

R&D资本具有“逐利性”的特征，其在区际间的流动主要受地区间利润率水平的影响，因此我们选取各地区规模以上企业的利润率作为吸引力变量来度量R&D资本的流动数量。目前，随着我国金融市场的不断完善和发展，R&D资本流动受距离的影响越来越小，但是这并不意味我们在使用引力模型度量R&D资本的流动量时不用考虑地区间距离因素的影响。根据引力模型理论，区域间的空间吸引力水平与其所处的地理空间位置有着密切的联系，任何地区与其它周围的地区之间均存在着经济联系，并且距离较近的地区比距离较远的地区经济联系更为紧密，这也符合地理学第一定律[24]，由此可知地理距离相近的地区之间经济相关性越强，其R&D资本的往来也会较为频繁。基于此，我们借鉴白俊红和蒋伏心(2015)的研究，使用地区间的距离表征区域间的经济关联程度，并使用各地区的利润率来表征R&D资本流动的吸引力变量，选用包含吸引力变量的引力模型对R&D资本的流动量进行核算[19]：

(4)

式(4)中，FCij为i省流动到j省的R&D资本量，cpi为i省的R&D资本存量，ratej是j省的规模以上企业的利润率水平，表征j省对i省R&D资本的吸引力，其余变量的解释与式(2)相同。

同样，从i省份流出的R&D资本总量可以用下式求得：

(5)

关于R&D资本流动量的度量，本文选用的是《中国科技统计年鉴》中各省份的R&D经费内部支出数据。由于R&D经费支出反映的是本年度内创新活动的投入量，是一项流量指标，但是其对R&D过程本身或者是R&D活动成果的影响均不仅仅局限于当期。一方面，R&D经费投入不仅会对当年的研发创新活动产生影响，其会形成一定的资本积累，在很长一段时间内发生作用，并且 R&D资本不仅包括资金部分，也暗含着知识积累部分，其资本积累越大说明形成的知识积累也越多，越有利于技术的进步；另一方面，从R&D经费投入到取得经济成果的过程需要大量的研究与试验工作，从而使得R&D经费效用的完全发挥存在时滞。基于R&D经费投入与经济活动的时间分布关系，国内外学者对R&D经费投入量的数据处理主要分为以下两种：

第一种是使用永续盘存法测算R&D资本存量，用R&D资本存量来反映当年研发活动的开展情况和知识的积累[25-26]。具体的测算方法如式(6)所示：

(6)

式(6)中Kit和Ki(t-1)分别表示区域i在t时期和t-1时期的R&D资本存量；m滞后期数，km为滞后系数，即R&D经费支出在滞后m期时的贴现系数。假设R&D影响的平均滞后期为λ，且t-λ期的R&D经费支出为t期R&D资本存量的增加量，当m=λ时，km=1，否则，km=0。σ为折旧率，本文采用国际上通用的做法取σ=15%；Ei(t-m)表示地区在t-m时期的R&D经费实际支出，其值应该按照R&D支出价格指数进行平减。假定R&D活动的平均滞后期λ=1年，则当m=λ=1时，式(6)变为式(7)：

Kit=(1-σ)×Ki(t-1)+Ei(t-m)

(7)

为了排除物价的影响，我们需要对R&D经费投入额进行平减。关于R&D支出价格指数的构造，本文参照了Loeb和Lin(1977)、岳书敬(2008)等人的研究，从R&D经费支出的明细构成来对R&D支出价格指数进行构造[27-28]。根据《中国科技统计年鉴》中对R&D经费支出的用途划分，将R&D经费分为用于日常性支出和资产性支出两类，计算出2000-2013年间这两类支出分别占R&D支出的比例。经计算最终得出R&D支出价格指数=0.6*消费价格指数+0.4*固定资产投资价格指数。

关于基期资本存量(K0)的核算，本文参照Hu等(2005)的研究[29]，用式(8)求得：

K0=E0/(η+σ)

(8)

式(8)中，E0为经过平减后的基期R&D经费投入实际值，η为考察期内R&D经费支出的增长率，经计算η的值为26%，σ为折旧率。

第二种是使用滞后期的R&D经费流量数据来反映R&D经费投入与经济成果间的关系，但是关于滞后期的选取，目前学界还没有达成统一的共识。Bode(2004)、苏方林(2006)等学者认为R&D经费投入对创新生产的影响在滞后1期时达到最大[30-31]；朱平芳和徐伟民(2005)以上海市大中型工业企业的专利产出量为研究对象，实证结果表明，当滞后4期时，R&D经费内部支出对专利产出的贡献最大[32]；项歌德等(2011)等以全国各区域的专利产出为研究对象，发现这一滞后期数最优为2[33]。

本文选用R&D资本存量来度量R&D资本在区际间的流动量。同时，出于稳健性的考虑，本文还采用滞后期的R&D经费数据进行测度，并借鉴Bode(2004)等人的研究，将滞后期数设置为1年[30]。

(二)生产率的测算

目前计算全要素生产率的方法主要有索洛余值法、数据包络分析法(DEA)、随机前沿法(SFA)等等。其中DEA方法是一种基于数学归纳的测算方法，其不需要预先设定函数的具体形式，不受投入、产出指标量纲的影响，能够客观地对全要素生产率进行测算。因此本文选用DEA-Malmquist生产率指数法测算各个省份的全要素生产率。

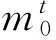
(9)

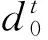
(10)

由于不同生产水平基期存在不同的数值，Färe等(1994)为了避免数值的差异，将上述两个数值的几何平均值作为从t时期到t+1时期的Malmquist指数的真实近似[13]，可得式(11)：

m0(xt,yt,xt+1,yt+1)=

(11)

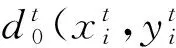
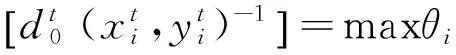
(12)

在具体实践中，本文选取中国大陆30个省级行政区为决策单元(西藏由于数据不全除外)，将各省的实际GDP作为产出变量，将各省的年平均就业人数以及固定资产投资作为投入变量。其中实际GDP是以2000年为基期，使用GDP平减指数进行平减后得到的；固定资产投资借鉴张军等(2004)的方法，采用永续盘存法核算成存量[34]。

四、模型构建与数据说明

根据空间计量经济学理论，区域生产率可能具有空间相关性的特征[35]。比如，如果某个地区具有较高的生产率，那么与之相邻或者相近的地区可能会受到“知识溢出”效应的影响，从而也会有比较高的生产率；在相邻或者相近区域的生产能力和生产效率得到提高的情况下，创新要素将在市场趋优机制的作用下，从本地区流动到生产效率更高的地区，这不仅不利于本地区经济的增长，而且会影响到本地区政府的政绩考核，在此情形下，本地政府在晋升压力的驱动下，亦会制定相应的政策措施来提高本地区的生产率水平。

上面所述的空间相关性是否在中国的区域生产中显著存在，将关系到本文计量模型的正确选择与建立。如果经济主体间存在空间相关性，经典经济计量分析中的假定条件将不再满足，其估计结果也会出现偏误，而空间计量分析方法则能够将这种空间相关性考虑在内，以计量方法识别和度量空间变动规律，真实客观地描述经济活动。基于此，本文首先选用空间统计学中常用的Moran I指数法对各省的全要素生产率的空间相关性进行检验。如果检验结果表明我国各省的生产率之间存在着显著的空间相关性，就需要采用空间计量经济学方法，建立加入空间权重的空间计量模型。如果检验结果表明我国各省的生产率之间没有显著的空间相关性，则可建立经典计量模型进行分析。

(一)检验生产率空间相关性的Moran I指数

Moran I指数的计算方法如式(13)所示：

(13)

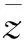
Moran I指数揭示了经济行为的全局空间相关性，取值范围为[-1，1]。该指数大于0表示经济行为空间正自相关，且指数越接近于1表示正相关性越强；小于0则表示经济行为空间负相关，且指数越接近于-1，表示负的自相关性越强。Moran I的值近似服从均值为E(I)，标准差为SD(I)的正态分布。可以利用E(I) 和SD(I)的值计算出近似服从标准正态分布的Moran I的表达式：

(14)

实践中，可利用(14)式的z值判断判断空间相关性的显著性。

表1报告了2000-2012年我国全要素生产率的Moran I指数。

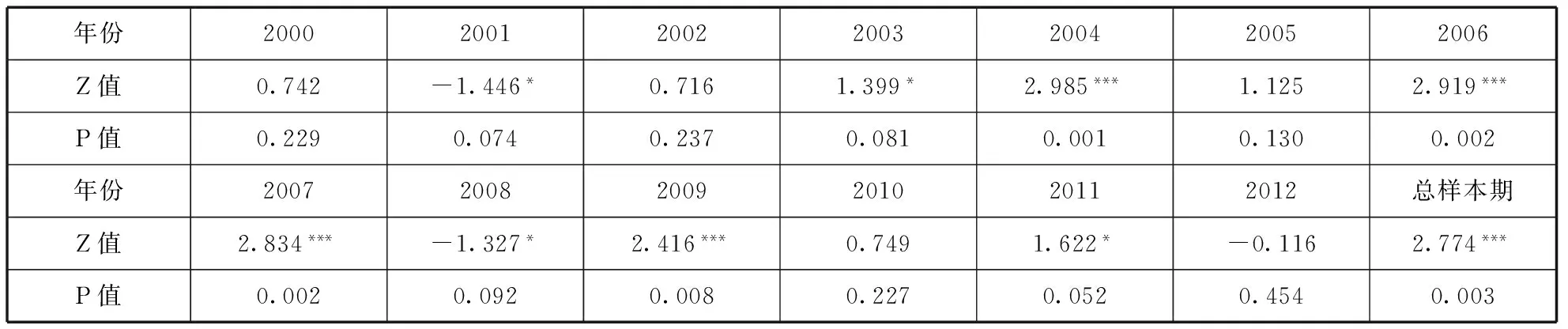
表1 2000-2012年我国全要素生产率的全局Moran I指数

注：括号内数字为显著性概率，***、**、*分别代表显著性水平小于0.01、0.05和0.1。

从表1可以看出，在考察期内，我国区域全要素生产率的总Moran I指数在5%的水平下显著为正，并且大部分年份的Moran I指数也均通过了显著性检验。这表明我国区域全要素生产率的分布并不是处于随机的状态，而是受到与之相邻省份的影响，在空间分布上具有明显的正向相关性。这为本文使用空间计量模型进行分析奠定了基础。

(二)空间面板计量模型的建立与数据说明

空间计量模型主要分为两种基本模型，即在经典回归模型中引入加入空间权重的内生变量的空间滞后(SAR)模型以及引入剩余项，假定空间相互作用是由外生冲击产生的空间误差(SEM)模型。

本文用SAR模型包含相邻省份的全要素生产率对本省份全要素生产率的空间影响因素。相应的模型表达式为式(15)：

Yit=αit+ρWYit+β1FPit+β2FCit+β3Xcontrol+μit

(15)

在式(15)中，Yit表示区域i在t时期的全要素生产率观测值，αit为截距项，ρ为空间自回归系数，W为空间邻接权重矩阵，μ为随机扰动项，其中Xcontrol为本文选取的一系列控制变量，在数据说明部分进行阐述。

用SEM模型来研究随机冲击所带来的空间相关作用对各省全要素生产率的影响。这种空间关联性主要体现在误差中，具体模型的表达式为式(16)：

Yit=αit+β1FPit+β2FCit+β3Xcontrol+μit

μit=λWμit+εit

(16)

(三)数据说明

为了更准确地描述创新要素流动对生产率的影响，本文对一些相关变量进行了控制。主要包括：反映政府行为的各级政府财政支出(Gov)、反映劳动力素质的人力资本水平(HR)、反映基础设施建设的铁路运营公里数(Rail)及反映中国市场化水平(MRK)的国有企业总产值占工业企业总产值的比重等。

财政支出(Gov)：宏观公共财政理论认为，一国生产率的增长与公共财政支出间呈正向相关性。原因是，财政支出规模越大，劳动力和资本的边际回报率越高，从而家庭储蓄和劳动者的积极性得到提升，新的发明创造不断涌现，生产率得到提升；然而，大量学者的实证研究却发现公共财政支出并不总能促进生产率的提升[36-37]，受财政支出规模和结构的影响，财政支出对经济活动的影响可能并不显著或呈现倒U形关系。鉴于此，本文选用各省的财政支出数据，以控制国政府的财政支出对全要素生产率的影响。

人力资本水平(HR)：人力资本质量的提升，一方面可以促进区域的技术创新水平得到提升，进而带动生产率的增长[38]；另一方面，还可以提升对新知识的效仿、学习能力，从而能够高效率地从创新要素流动所伴随的知识溢出中获取收益，使这些新知识快速转化为自身的创新生产能力，从而促进本区域生产率水平的提升。本文用劳动力平均受教育年限来衡量各省的人力资本水平，具体计算方法由各学历层次所需年限数乘以各学历人才占总人口的比重加总得到。

基础设施建设(Rail)：交通基础设施的完善一方面可以为创新活动的开展提供便利的条件支撑，助推创新活动产业链的形成；另一方面可以缩减R&D人员区际流动以及研发设备区际运输的时间成本和物质成本，从而可以有效地促进创新要素的跨区域迁移以及创新技术的区域扩散，促使研发资源得到有效的配置。本文选取各省份的人均公路里程数来表征交通基础设施建设情况。

市场化水平(MRK)：市场化水平是影响转型期中国市场配置资源的程度，反映知识溢出水平的一项重要指标[39]。市场化水平较高的区域具有知识分散速度快、知识员工流动性较强、风险投资规模较大等特点，这些因素均有利于高水平生产活动的开展以及生产率的提升。但是另一方面，市场化程度高的区域可能会面临着资源配置扭曲以及过度依赖外部知识技术的风险。本文选取我国国有企业总产值占工业企业总产值比重来衡量我国的市场化程度。

本文的原始数据来源于历年的《中国统计年鉴》和《中国科技统计年鉴》。考察样本为中国大陆30个省级行政区域(西藏由于数据不全除外)，研究时间段为2000-2013年，并且所有的数据均以2000年为基期。其中，测算全要素生产率的所使用的投入产出数据的时间跨度为14年(2000-2013年)，所测算出来的各项指数的变动情况有13年的数据，因此在空间面板计量模型中各变量的时间跨度为2000-2012年。除投入产出变量有420个观测值外，其余变量均有390个观测值。表2给出了本文选用变量数据的描述性统计结果。为了消除异方差的影响，除全要素生产率和比例值市场化程度取原值外，其余变量在模型的估计中均取对数。

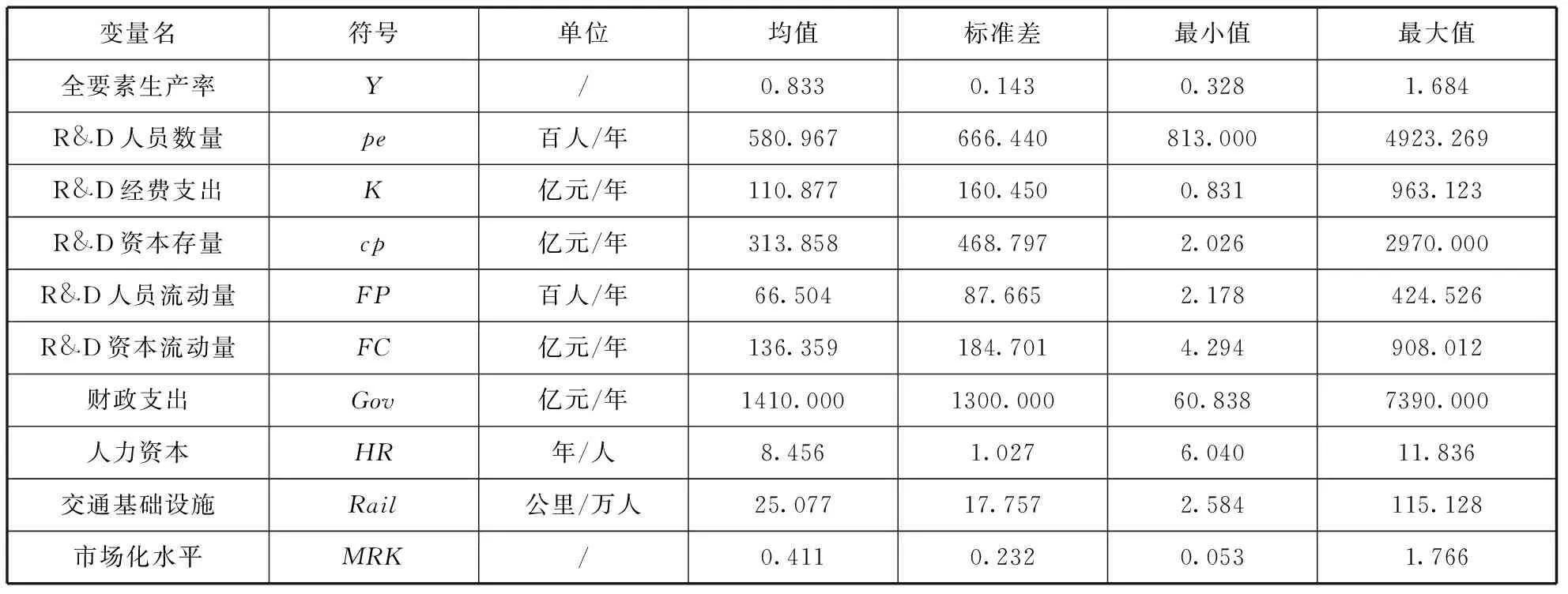
表2 变量的描述性统计

五、实证检验及分析

(一)实证结果

经Hausman检验，我们选用固定效应模型。利用MATLAB.R2014b软件计算得出的上述模型的具体估计结果如表3所示。其中，根据固定效应模型对地区和时间两类非观测效应的不同控制，我们分别对无固定效应(nonF)、地区固定时间不固定(sF)、时间固定地区不固定(tF)以及时间地区均固定(stF)四种效应进行了估计。

根据表3的估计结果，在8个空间面板数据模型中，地区固定时间不固定(sF)的空间滞后(SAR)模型的估计系数显著的个数最多，同时拟合得到的调整后R2和对数似然值也较高，因此我们选取该模型对影响全要素生产率的因素进行分析。

从sF效应的SAR模型的估计结果来看，R&D资本流动的回归系数显著为正，表明R&D资本的跨区域自由流动对我国全要素生产率的提升有显著的促进作用。R&D人员的流动对全要素生产率的影响并不显著，这与我们的预期不同。可能的原因在于，R&D人员在区际间的流动所伴随的空间知识溢出、资源优化配置和创新合作效应虽然能够促进我国全要素生产率的提升，但是目前我国市场化改革虽然已经取得了巨大的成就，但尚存在不完善的地方，比如当前我国区域间就业信息的交换还比较滞后，使得R&D人员可能并不能及时掌握和自有技能相关的招聘信息，从而使其在区际间的流动在一定程度上还具有盲目和滞后性；另外，我国各省区的地方保护主义倾向严重，地方政府官员在“晋升锦标赛”的压力下，可能会压低企业成本，给R&D人员提供特殊待遇，使本区域R&D人员的流动具有更高的隐性成本和心理成本；此外，基础条件优越的地区在吸引大量R&D人员流入的同时也会面临研发配套设施使用拥挤的困境。上述原因的存在，可能使得我国R&D人员流动的负面效应暂时大于正面效应，R&D人员流动对生产率的积极影响并没有完全发挥出来。

(二)稳健性检验

创新要素的流动是本文的关键解释变量，其科学设置尤为重要。为了保证回归结果的稳定性，本文将衡量地区吸引力的平均工资替换为人均GDP对 R&D人员的区际流动量进行度量，将R&D资本存量替换为滞后1期的R&D经费流量对R&D经费的区际流动量进行度量，重复上述步骤对计量模型重新进行回归分析。结果见表4。

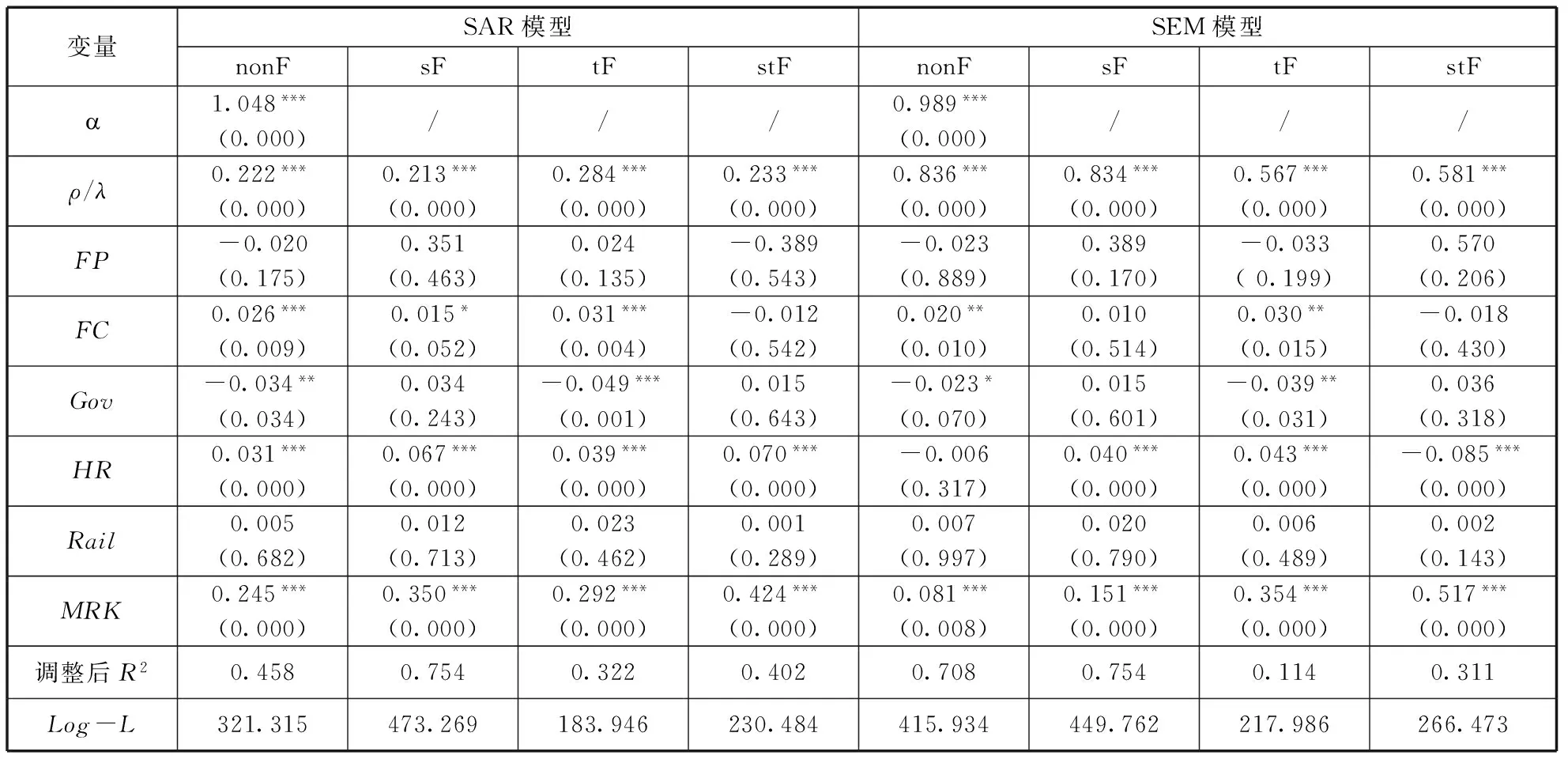
表3 空间面板计量回归结果

注：括号内数字为显著性概率；***、**、*分别代表显著性水平小于0.01、0.05和0.1；“/”表示此项为空。

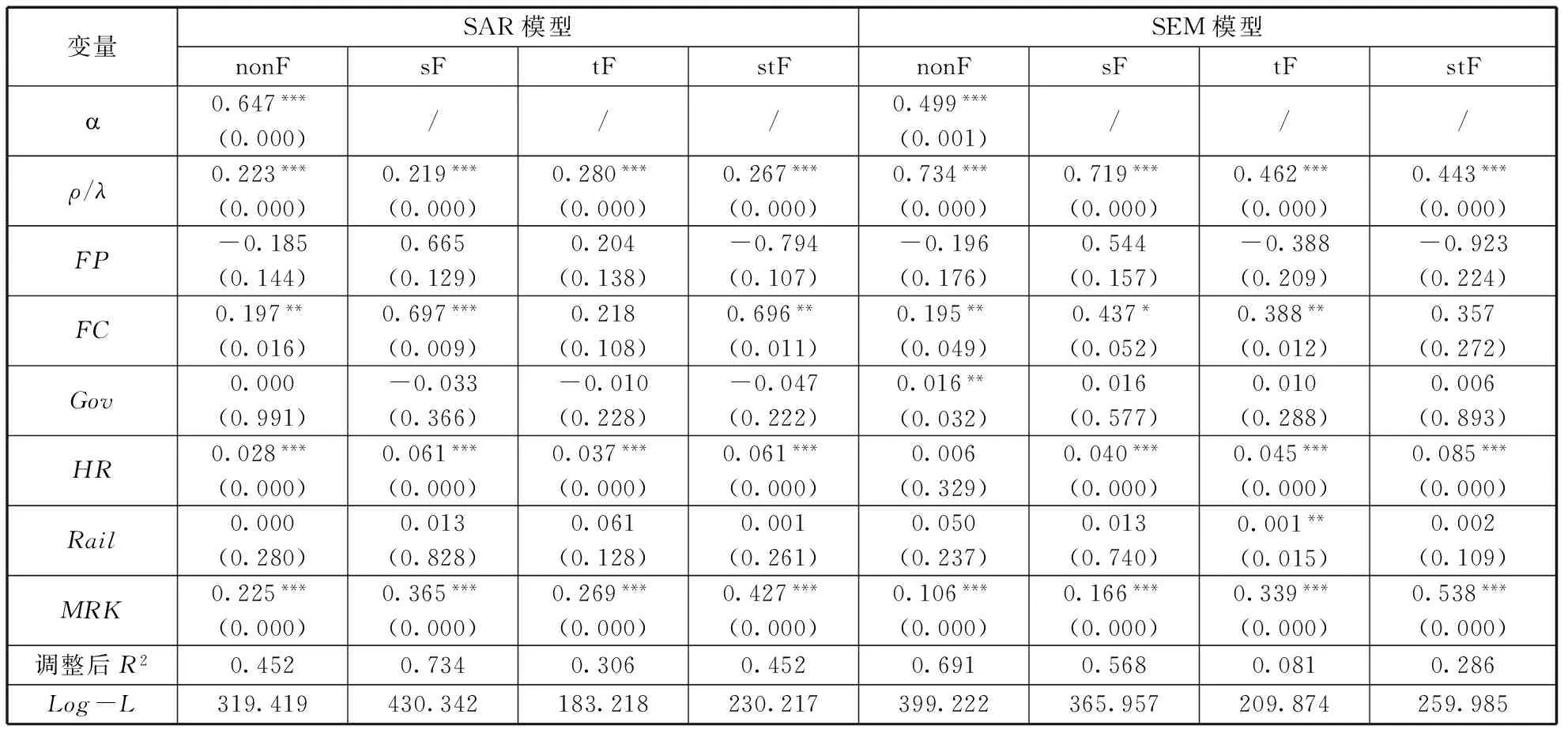
表4 稳健性检验结果

注：括号内数字为显著性概率；***、**、*分别代表显著性水平小于0.01、0.05和0.1；“/”表示此项为空。

从表4可以看出，sF效应的SAR模型仍具有最优的拟合效果。回归系数显示R&D资本在区际间的流动与全要素生产率之间仍然具有显著的正相关关系，R&D人员流动对全要素生产率的影响并不显著。这与表3中的估计结果相类似，表明前文中的研究结果并没有因为引力模型中不同指标的选取而出现较大的差异，且不论使用R&D资本存量还是滞后期的R&D经费流量对R&D资本区际流动量进行测度，对本文的实证研究结果并没有较大的影响。综上所述，本文实证研究的结果具有良好的稳健性。

六、结论与启示

本文利用2000-2013年中国大陆30个省级行政区的面板数据，在充分考虑全要素生产率空间相关性的基础上，运用空间面板计量分析技术，实证考察了创新要素流动对全要素生产率的影响。研究发现，我国各省份间的全要素生产率存在着显著的空间相关性，区域间的生产活动是一个相互联系的整体；R&D资本的流动显著地促进了全要素生产率的提升，而R&D人员的流动对全要素生产率的影响并不显著。

上述结论对于科学合理地引导创新要素的流动，实现研发资源的合理配置，推动中国创新型国家建设和全要素生产率的持续提升具有重要的启示作用。

第一，进一步完善我国资本市场的建设，充分发挥市场机制在资本配置中的作用，实现R&D资本在区际间的自由流动，从而促进我国区域生产率的提升。此外，由于R&D资本具有高度的风险性和资产专用性等特征，金融机构应当为R&D资本的跨区域流动提供相应的风险预测平台指导，创新金融与科技的合作模式，为R&D专项资金的流动提供多种渠道和相应的金融支持。

第二，鉴于区域生产活动的空间相关性特征，R&D人员的流动不仅对流入地有利，其还可以通过知识溢出等途径，带动整个区域经济的发展。因此进一步消除地方保护主义行为，减少限制R&D人员流动的行政壁垒，加快构建完善的跨区域研发岗位市场信息体系，对于促进我国R&D人员在区际间的合理流动具有重要意义。此外，R&D人员流入量较大的地区要适当加大研发基础设施投入，避免由于研发设备使用“拥挤”而影响区域生产率的增长。

本文的研究也存在一些局限。由于数据方面的限制，本文只考察了创新要素在区际之间的流动，而实际上创新要素在各个区域内部的流动亦可能对区域生产率产生重要影响。我们也将在后续研究中对其给予持续关注。

[1]AUER P, BERG J, COULIBALY I. Is a stable workforce good for productivity? [J]. International Labor Review, 2005, 144(3):319-343.

[2]KLEINKNECHT A, OOSTENDORP R M, PRADHAN M P, et al. Flexible labor, firm performance and the Dutch job creation miracle[J]. International Review of Applied Economics, 2006, 20(2): 171-187.

[3]LIU X L, WHITE S. An exploration into regional variation in innovation activity in China [J]. International Journal of Technology Management, 2001, 21(1-2):114-129.

[4]官建成, 刘顺忠. 区域创新机构对创新绩效影响的研究[J]. 科学学研究, 2003, 21(2):210-214.

[5]DUGUET E, MACGARVIE M. How well do patent citations measure flows of technology? Evidence from French innovation surveys[J]. Economics of Innovation and New Technology, 2005, 14(5): 375-393.

[6]白俊红, 江可申, 李 婧. 应用随机前沿模型评测中国区域研发创新效率[J]. 管理世界, 2009(10)：51-61.

[7]朱平芳, 徐伟民. 政府的科技激励政策对大中型工业企业R&D投入及其专利产出的影响——上海市的实证研究[J]. 经济研究, 2003(6):45-53.

[8]孙文杰, 沈坤荣. 人力资本积累与中国制造业技术创新效率的差异性[J]. 中国工业经济, 2009(3):81-91.

[9]张海洋. R&D两面性、外资活动与中国工业生产率增长[J]. 经济研究, 2005 (5):107-117.

[10]吴延兵. R&D与生产率：基于中国制造业的实证研究[J]. 经济研究, 2006(11):60-71.

[11]朱有为, 徐康宁. 研发资本累积对生产率增长的影响——对中国高技术产业的检验 [J]. 中国软科学, 2007 (4):57-67.

[12]戴魁早. 中国高技术产业研发投入对生产率的影响[J]. 研究与发展管理, 2011, 23(4):66-74.

[14]BROEKEL T, GRAF H. Structural properties of cooperation networks in Germany: From basic to applied research[R]. Jena Economic Research papers, 2010.

[15]高丽娜, 蒋伏心. 创新要素集聚与扩散的经济增长效应分析——以江苏宁镇扬地区为例[J]. 南京社会科学, 2011 (10):30-36.

[16]ROMER P. Endogenous technological change [J]. Joumal of Political Economy, 1990, 98(5):71-102．

[17]ALMEIDA P, KOGUT B. Localization of knowledge and the mobility of engineers in regional networks [J]. Management Science, 1999, 45(7):905-917.

[18]毕先萍. 劳动力流动对中国地区经济增长的影响研究[J]. 经济评论, 2009(1):48-53.

[19]白俊红, 蒋伏心. 协同创新、空间关联与区域创新绩效[J]. 经济研究, 2015(7):174-187.

[20]ANDERSON J E. A theoretical foundation for the gravity equation [J]. American Economic Review, 1979, 69(1):106-116.

[21]BERGSTRAND J H. The gravity equation in international trade: some microeconomic foundations and empirical evidence [J]. Review of Economics and Statistics, 1985, 67(3): 474-481.

[22]ANDERSON J E, Wincoop E. Gravity with gravitas: A solution to the border puzzle [J]. American Economic Review, 2003, 93(1): 170-192.

[23]LEE E S. A theory of migration [J]. Demography, 1966, 3(1): 47-57.

[24]TOBLER W R. A computer movie simulating urban growth in the detroit region [J]. Economic Geography, 1970, 46(2): 234-240.

[25]GOTOA, SUZUKI K. R&D capital, rate of return on R&D investment and spillover of R&D in Japanese manufacturing industries [J]. Review of Economics and Statistics, 1989, 21(4):555-564.

[26]白俊红. 中国的政府R&D资助有效吗？来自大中型工业企业的经验数据[J]. 经济学(季刊), 2011, 10(4):1375-1400.

[27]LOEBP，LIN V. Research and development in the pharmaceutical industry: A specification error approach [J]. Journal of Industrial Economics, 1977, 36(1):45-51.

[28]岳书敬.中国区域研发效率差异及其影响因素——基于省级区域面板数据的经验研究[J]. 科研管理, 2008, 29(5):173-179.

[29]Hu A G Z, JEFFERSON G H, QIAN Jin Chang. R&D and technology transfer: Firm-level evidence from Chinese industry [J]. Review of Economics and Statistics, 2005, 87(4):780-786.

[30]BODE E. The spatial pattern of localized R&D spillovers: An empirical investigation for Germany [J]. Journal of Economic Geography, 2004, 4 (1):43-64.

[31]苏方林. 中国省域R&D溢出的空间模式研究[J]. 科学学研究, 2006, 24(5): 698-701.

[32]朱平芳, 徐伟民. 上海市大中型工业行业专利产出滞后机制研究[J]. 数量经济技术经济研究, 2005, 22 (9):136-142.

[33]项歌德, 朱平芳, 张征宇. 经济结构、R&D投入及构成与R&D空间溢出效应[J]. 科学学研究, 2011, 29(2):206-214.

[34]张 军, 吴桂英, 张吉鹏. 中国省际物质资本存量估算:1952-2000[J]. 经济研究, 2004, (10):35-44.

[35]ANSELINL. Spatial econometrics: methods and models [M]. Dordrecht：Kluwer Academic Publishers, 1988.

[36]DEVARAJAN S, SWAROOP V, ZOU H F. The composition of public expenditure and economic growth [J]. Journal of Monetary Economics, 1996, 37(2): 313-344.

[37]曾淑婉. 财政支出、空间溢出与全要素生产率增长——基于动态空间面板模型的实证研究[J]. 财贸研究, 2013, 24(1):101-109.

[38]LUCAS R E. On the mechanics of economic development [J]. Journal of Monetary Economics, 1988, 22(1): 3-42.

[39]孙 早, 刘李华, 孙亚政. 市场化程度、地方保护主义与R&D的溢出效应——来自中国工业的经验证据[J]. 管理世界, 2014(8):78-89.

(本文责编：王延芳)

Why Is the Flow of R&D Elements So Important：Perspective of Total Factor Productivity

WANG Yue，LIU Bing-lian

(InstituteofUrbanandRegionalEconomics,NankaiUniversity,Tianjin300071,China)

This paper aimed to reveal the influence of the R&D elements’ flow on the total factor productivity in china. It first analyzed the reason why R&D elements’ interregional flow can affect productivity in theory. It then used the method of spatial econometric analysis to make an empirical test on the relationship between R&D elements’ interregional mobility and total factor productivity, by using provincial panel data from Chinese 30 provinces. It is found that the regional total factor productivity has spatial correlation effect obviously, and the R&D capital’s mobility could significantly make a positive effect on regional total factor productivity. After considering the mobility of R&D factors in different form of gravity model, The conclusions of the article provide a useful reference for drafting China’s R&D elements’ interregional flow policy scientifically, which is of great benefit to promoting China’s continuous improvement of productivity.

interregional flow of R&D elements; total factor productivity; spatial econometric

2017-01-05

2017-06-06

国家自然科学基金(项目批准号：71573138)；教育部人文社会科学研究专项任务项目(项目批准号：16JDGC009)。

王 钺(1991-)，女，河南南阳人，南开大学经济学院城市与区域经济研究所博士生，研究方向：区域创新管理。通讯作者：刘秉镰。

F283

A

1002-9753(2017)08-0091-11