平面团簇稳定结构的蒙特卡罗树搜索∗
2017-09-07何长春廖继海杨小宝
何长春 廖继海 杨小宝
(华南理工大学物理与光电学院,广州 510640)
平面团簇稳定结构的蒙特卡罗树搜索∗
何长春 廖继海 杨小宝†
(华南理工大学物理与光电学院,广州 510640)
(2017年4月7日收到;2017年6月18日收到修改稿)
以平面团簇为例提出了一种结合结构识别和蒙特卡罗树技术搜索稳定结构的新方法.体系原子之间的相互作用由两类模型势能函数来描述:Lennard-Jones二体势函数与基于Lennard-Jones势的三体势函数.考虑可能的三角晶格碎片作为候选结构,引入编号策略对结构进行快速识别,并运用蒙特卡罗树搜索研究稳定结构随着原子数增大的演化过程;对于能量较低的候选结构,进一步采取局域优化来获得对应体系的稳定结构.计算表明,Lennard-Jones二体势函数对应的三角晶格团簇更稳定;在特定的参数下,三体势函数对应的六角晶格团簇更稳定.结合结构识别和蒙特卡罗树搜索可以对候选结构空间进行高效扫描,在较短时间内更容易搜索到稳定的团簇结构,并可以与第一原理计算结合实现材料的结构预测.
团簇,结构识别,蒙特卡罗树,全局优化
1 引 言
团簇一般由从几个到上千个原子组成,是宏观世界与微观世界的连接纽带,结构丰富并具有很多奇特的性质,在物理、化学、材料等领域具有重要的研究价值[1−4].幻数(magic number)是团簇的重要特征之一[5],而幻数结构的确定在原子团簇的研究中具有相当重要的作用[6].近些年来,各种各样的原子或分子团簇陆续在实验中被制备出来,也引起了理论工作者的广泛关注[7].例如,实验中发现惰性气体的团簇往往呈现出高对称结构[8];理论研究指出,金属团簇在尺寸较小的时候是高对称结构,而Ru55,Rh55,Pd55等的稳定结构不是高对称性的正二十面体结构,而是面心立方结构对应的晶格碎片[9].实验中制备了不同尺寸的石墨烯量子点,发光频率覆盖所有可见光范围,其对应的结构是平面六角结构的晶格团簇[10];在从石油中提取和分离出来的纳米金刚石团簇,也是金刚石结构的晶格碎片[11,12].有趣的是,体相的硼是由正二十面体堆积起来的结构,而硼团簇倾向于形成平面三角结构,随着原子数的增大体系将出现空位,出现由原子和空位形成的“合金”结构[13,14].
理论对团簇的结构和性质研究也有很多相关的工作,其中包括对结构能量的评价以及不同结构的变换和筛选.一般来说,第一原理计算对能量的评价精度高,但比较耗时,同时局域优化方法(准牛顿法、共轭梯度法等)对初始结构依赖严重.在做结构搜索时,我们通常需要借助势能函数简化能量的计算来提高搜索效率;然而,即使在给定的势能函数的条件下,寻找原子团簇的最优结构在理论上被证明为NP-Hard问题,通常需要利用启发式智能算法进行优化计算,使得候选结构中不陷入局域最小值,实现全局最优的结构搜索,常见的方法包括遗传算法[15]、粒子群算法[16]、蒙特卡罗模拟退火算法[17]、分子动力学模拟[18,19]等.邵桂芳等[20]选择经验势能来描述原子间相互作用,运用改进的Basin-Hopping Monte Carlo算法,研究了不同尺寸和不同比例下的Fe-Pt二元合金团簇.张林等[21]结合遗传算法和基于密度泛函理论的紧束缚方法(density functional tight binding,DFTB),搜索发现SimGe9−m团簇存在的两种低能原子堆积稳定构型.潘必才等[22]运用两种结构搜索方法(压缩液态法、遗传算法)与锗的紧束缚模型势相互结合,确定了Ge65,Ge70,Ge75的能量较低的可能结构,发现这三种团簇均具有两类稳定、能量相近的异构体:类球形和类椭球形.值得注意的是,在结构搜索过程中,如果不进行结构检查容易导致重复计算而降低搜索效率.基于微粒群和遗传算法等全局优化方法,两类常用的搜索软件Calypso[23]和Uspex[24]都提出了表征结构相似性的算法,可以实现高效的结构搜索.
理论上要确定团簇的幻数结构,我们需要在给定原子数的条件下搜索能量最低结构,再根据能量随原子数变化曲线的局域极值来实现.Greiner等[25]选择Lennard-Jones势描述原子之间的相互作用,运用团簇生长模型,在 N 个原子的最稳定团簇基础上寻找 N+1个原子团簇的最稳定结构,被证明是一种效率较高的搜索方法.以平面团簇的结构搜索为例,我们用Lennard-Jones势函数描述原子之间相互作用.我们选择三角晶格团簇作为初始结构,引入编号方法对结构进行识别检查,避免相同结构重复的能量评价,可以很好地提高搜索效率.考虑到不同大小的晶格团簇互相联系,我们采用蒙特卡罗树技术[17],以低能量为目标进行搜索.该方法可以同时兼顾到搜索的深度和广度,可以很好地增加样本的多样性,提高低能量结构搜索的成功率.在找到能量较低的结构后,我们进一步对结构进行局域优化,获得体系的最稳定结构.
2 计算方法
我们的搜索方法主要包括结构识别和蒙特卡罗树技术.选择的初始结构是晶格团簇,可以根据对称性严格检查两个结构是否全同;蒙特卡罗树技术可以建立不同原子数构型之间的联系,同时根据体系能量的高低对不同分枝进行重要性抽样.
2.1 结构识别
使用坐标描述给定团簇的构型是简单易行的方法,但在结构识别时很不方便.以平面三角晶格团簇为例,我们按照编号的方法对结构命名,可以实现快速的结构检查.首先,我们在三角晶格平面上选择一个格点为原点,根据其他格点到原点距离由小到大进行编号:对于距离相同的格点,我们从极角最小者开始,按照逆时针方向从小到大进行编号,格点的编号如图1(a)所示.接着,对于给定的三角晶格团簇,我们可以在已经有编号的平面上,通过各个原子的坐标分别找到对应的编号,并从小到大排序,获得一组编号表示该结构(注意:此时等价的结构有多个可能的编号).最后,我们考虑可能的平移、反演、旋转等平面三角晶格允许的对称操作,并记录所有可能的编号数组,找出最小的编号作为该结构对应的编号(我们从第一个分量开始逐次比较大小,如果第一个的分量相同就考虑下一个分量,以此类推,比如[1-2-3]小于[1-3-4]),此时获得的编号和结构一一对应.结构检查时只需要比较两个编号是否完全相同即可,从而有效提高了程序的运行效率.当原子数为4时,共有七种同分异构体,其结构以及对应的编号如图1(b)所示.

图1 (网刊彩色)(a)三角晶格背景格点编号;(b)原子数为4时的七种同分异构体及其对应的编号Fig.1.(color on line)(a)The nuMbered triangu lar lattice;(b)seven isoMers With 4 atoMs and the corresponding nuMber series.
2.2 蒙特卡罗树搜索技术
对于平面三角晶格团簇,我们根据编号方法可以很快遍历得到原子数不大于10的全部结构(其中原子数是10时对应的结构数为30490),并根据势能函数计算获得体系的最优结构.随着原子数的增多,可能的候选结构数目急剧上升,这要求我们只能选择有限数量结构来继续增加原子.然而,简单选择一些能量较低的结构,容易让体系陷入局域最优;过多选择结构,在有限的时间内很难得到较为稳定的结构.因此,我们借鉴了用于处理连续决策优化问题的上限信心策略(upper confidence bound).该算法最初是为了研究多臂赌徒模型(mu lti-armed bandit Model)[26,27],核心在于计算其信心索引Ij:
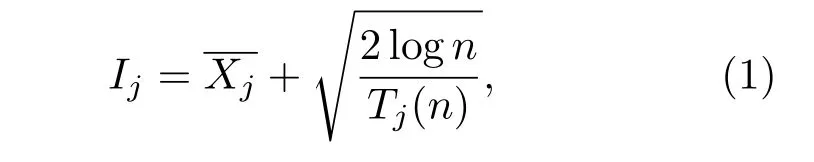
本文算法的流程图如图2(a)所示:我们根据初始的原子数为N的结构,按照能量的大小,依照玻尔兹曼分布进行重要性抽样得到一定数目的样本,样本j被抽到的概率Pj表示为

这里Ej是结构样本中第j个结构的能量;k是玻尔兹曼常数;T是温度,用来调节搜索的广度与深度.在这些样本上增加一个原子拓展得到N+1个原子的结构,最后对能量最低的100个候选结构进行局域优化.图2(b)给出原子数为3的结构通过选择-拓展-选择得到原子数为4的结构的示例.首先,原子数N=3时有三个不等价结构,根据(2)式进行重要性抽样得到两个结构,然后对这两个结构进行完全拓展得到原子数N=4的六个结构,再根据(2)式进行重要性抽样得到三个结构,实际操作中我们选取每次抽样的样本数目随着原子数的增加而相应增加,重复进行上述操作得到原子数更多的结构.
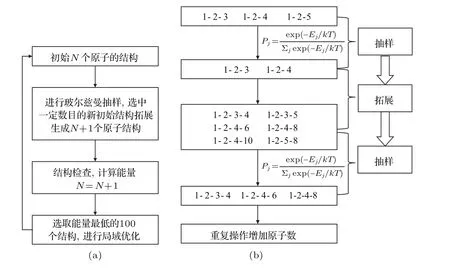
图2 (a)搜索算法流程图;(b)原子数从3到4的操作举例Fig.2.(a)The fl oWchart of the search algorithm;(b)the exaMp le for the case froMN=3 to N=4.
相邻原子数对应的结构互相关联,我们可以得到类似“树”一样的结构,在10个原子以内通过遍历得到的是完整的“树”.之后,我们根据能量的高低进行了剪枝,使得“树”出现非对称性随机生长,倾向于保留能量较低的结构,可以有效缩小范围并提高搜索效率.这里,我们在树的每一层以一定概率选取初始的父结构,然后在这些结构中进行拓展计算出能量最低的结构,并根据概率选择作为下一层的初始结构,并通过循环操作不断增加体系的原子数.其中概率是按照玻尔兹曼分布设置的,如(2)式所示.可以看到,能量越低的结构被选中的概率越大,但是能量较高的结构仍有被选中的概率,可以保证样本的多样性,避免陷入局域极小值.(2)式中的T类似于模拟退火算法中的温度,温度越小则全局最小的结构被搜索出来的概率越高.当T趋于零时,该算法将趋于完全的深度搜索;T趋于无穷大时,该算法将趋于完全的广度搜索.
3 结果与讨论
为了检验算法的有效性,我们选择了两类势能函数描述原子之间的相互作用,并搜索了给定势函数下不同原子数的稳定结构.
3.1 Lennard-Jones势
首先,我们考虑体系中粒子之间的相互作用符合Lennard-Jones势函数,则体系的总能量V为
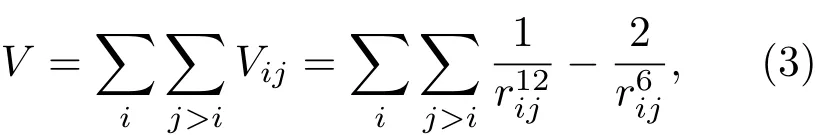
其中rij为原子i,j之间的距离.图3给出了我们搜索得到的最低的平均能量趋势图以及幻数所对应的稳定结构.在该势能函数下,原子倾向于形成尽可能多的最近邻,在平面结构中对应的是六个最近邻,同时要求团簇的边界呈凸包络,可以使得边缘的悬挂键数目比例最低,增加体系稳定性.图4给出了原子数较多时对应的幻数结构.可以看出,幻数所对应的结构往往具有较高的对称性,边界对应的是六边形;随着原子数的增多,稳定结构包含了所有的正六边形的结构,例如原子数为19,37,61,91时,分别对应于边长为2,3,4,5的正六边形.
图3中用×表示的即为在搜索空间下所访问过的结构的平均原子能量,我们称之为候选结构.这里在每一次的循环操作中将会以(2)式的概率随机选取一定数量的结构进行拓展,以生成N+1个原子的结构,在N≤100时一共计算了8×105个结构.将给定原子数的最低能量的平均值连接起来即为图3中的折线.
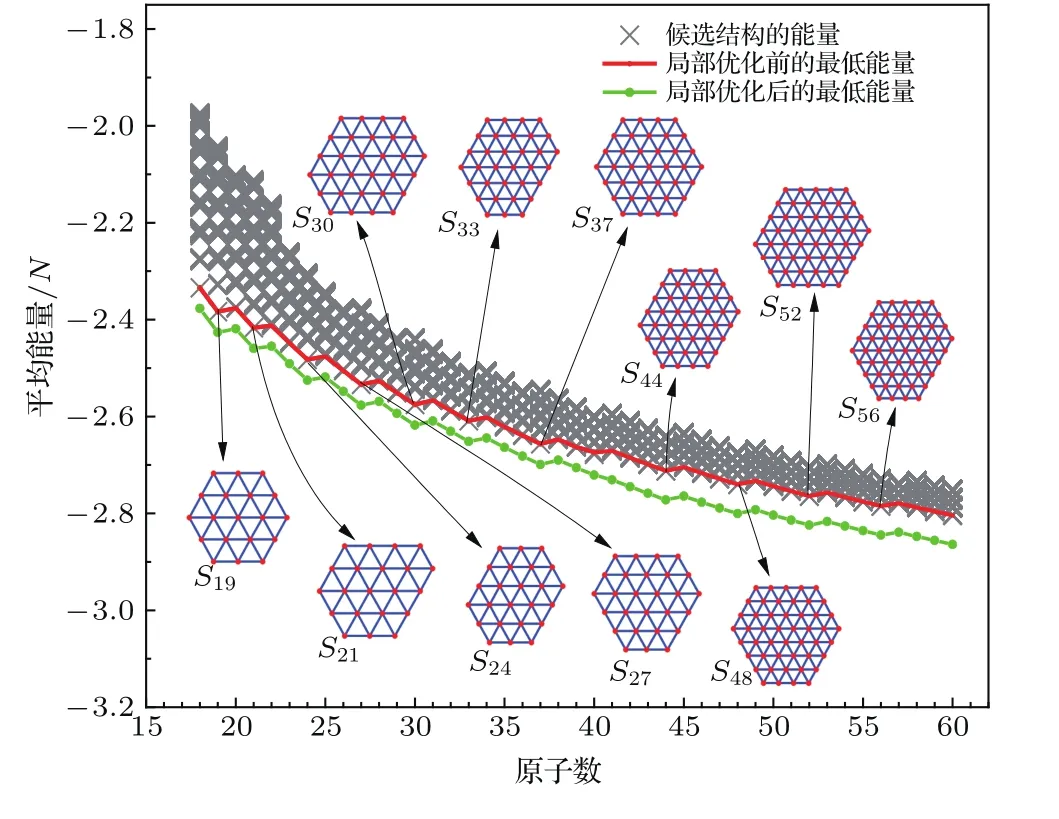
图3 (网刊彩色)Lennard-Jones势函数下原子团簇平均能量的变化趋势Fig.3. (color on line)The average energy of clusters as a function of the nuMber of atoMs under the Lennard-Jones potential.
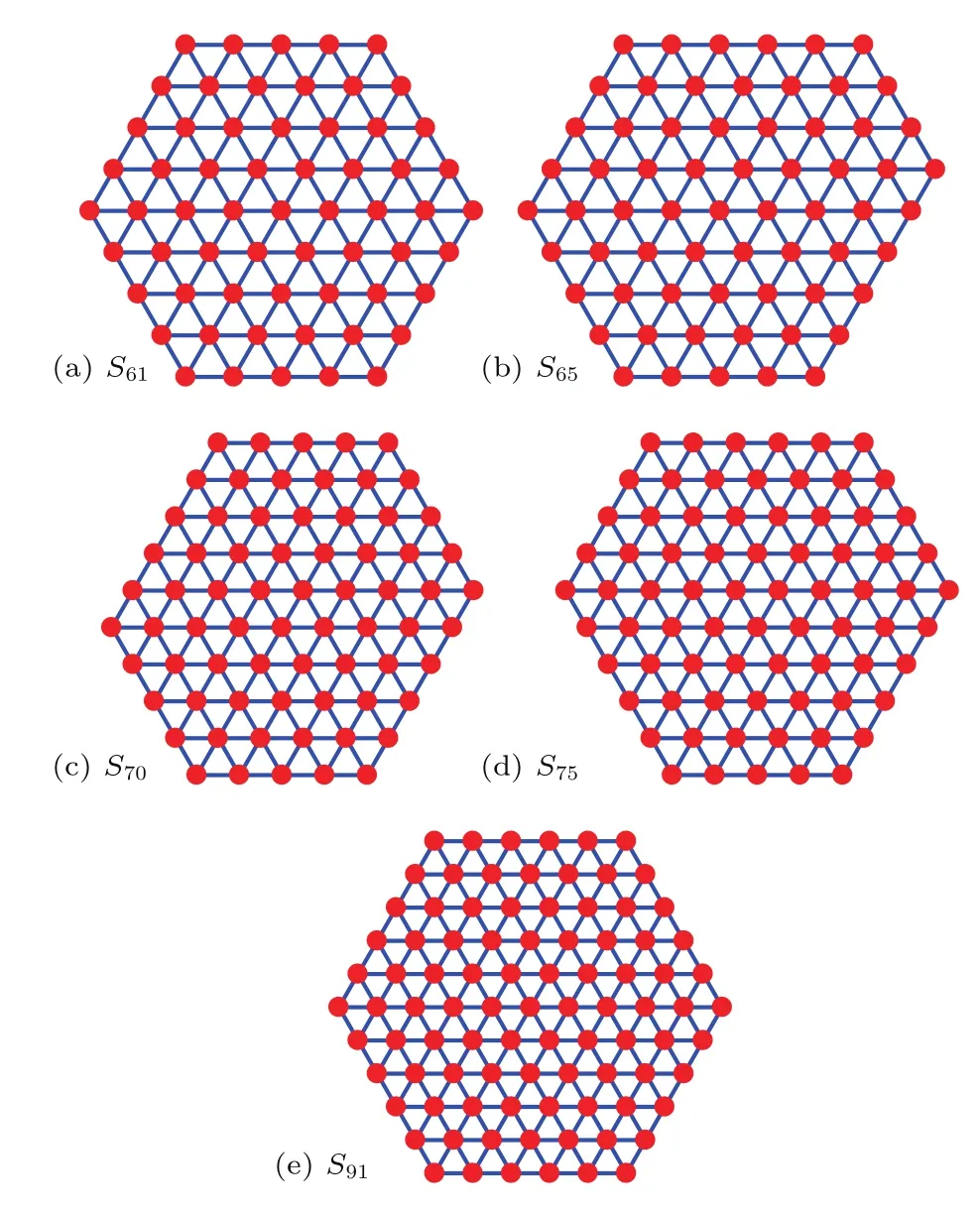
图4 (网刊彩色)Lennard-Jones势函数下的幻数Fig.4.(color on line)TheMagic nuMber structures.
利用蒙特卡罗树搜索,我们可以得到能量较低的三角晶格团簇,属于平面密堆结构,与Yang和Zhang[29]之前工作相符合.在本文的算法中,35个原子以内的体系通常需要计算体系的势函数1000—3000次就可以搜索到基态结构,而36—50个原子的体系则需要评价3000—5000次,但是一般的微粒群算法需要对结构进行8000次的评价才可以搜索出基态结构,可见本文的算法在结构搜索的效率上有了一定的提升.我们可以进一步对能量较低的候选结构进行局部优化,这里我们使用的是最速下降法.由图3可以看出,局部优化后的结构的能量均有所下降(如图3中的点划线所示),但原子位置没有很大的变动,对应的幻数也没有变化.
3.2 Lennard-Jones三体势函数
作为比较,我们接下来考虑的体系中,粒子之间的相互作用包括二体作用与三体作用,此时体系的总能量V为
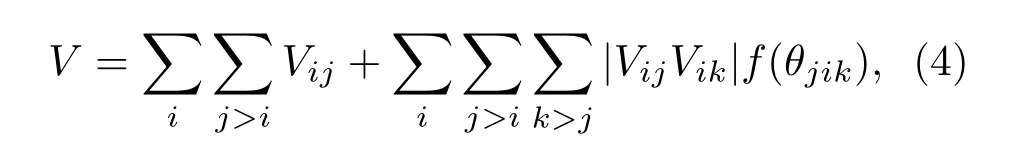
这里θjik表示向量rij,rik之间的夹角,Vij和Vik分别表示为原子i与原子j和k之间的二体作用势. 特别地,这里我们取f(θ)=|θ− 2π/3|,所以θ=2π/3时f(θ)最小,从而使得基态体系容易形成角度为2π/3的键角.
我们利用类似的方法进行结构搜索,对应的幻数结构和能量变化曲线如图5所示.该势函数由两部分贡献,第一部分使得体系原子之间距离倾向于为1,第二部分使得体系的成键键角倾向于2π/3.在该势函数下,原子团簇倾向于形成类似石墨烯的碎片结构.由图5可见,这些较为稳定的原子团簇结构是不断向外生长出来的正六边形.比如S10,S14,S16分别对应的是萘、蒽、芘的结构,S24对应于轮烯的结构.需要说明的是,基态结构和f(θ)的具体形式有关,当改变f(θ)的极值点,基态的结构会发生较大的变化.

图5 (网刊彩色)Lennard-Jones三体势函数下原子团簇的平均能量变化趋势Fig.5. (color on line) The average energy of clusters as a function of the nuMber of atoMs under the Lennard-Jones th ree body interaction potential.
4 结 论
本文提出了一种结合结构识别和蒙特卡罗树技术搜索稳定结构的新方法.以平面团簇为例,我们考虑了包含二体和三体相互作用的Lennard-Jones势函数,并搜索确定了不同原子数的稳定结构.我们选择三角晶格团簇作为候选结构,引入编号策略对结构进行快速识别,并选择能量较低的候选结构进行局域优化来获得对应体系的稳定结构.我们的算法避免了相同结构的重复计算,建立了相邻原子数的晶格团簇的互相联系,采用蒙特卡罗树技术兼顾搜索的深度和广度.该方法可以对候选结构空间进行高效扫描,在较短时间内更容易搜索到稳定的团簇结构,并可以与第一原理计算方法结合,进行真实材料体系的结构搜索.
[1]Baletto F,Ferrando R 2005 Rev.Mod.Phys.77 371
[2]Gong X F,Wang Y,N ing X J 2008 Chin.Phys.Lett.25 468
[3]Liu T D,Zheng JW,Shao G F,Fan T E,Wen Y H 2015 Chin.Phys.B 24 33601
[4]Zhang M,Gao Y,Fang H P 2016 Chin.Phys.B 25 13602
[5]de Heer WA 1993 Rev.Mod.Phys.65 611
[6]K night WD,C leMenger K,Heer WA D,Saunders WA,Chou MY,Cohen ML 1984 Phys.Rev.Lett.52 2141
[7]Honeycutt J D,Andersen H C 1987 J.Phys.Chem.91 4950
[8]Liu G Q,Zhang Y L,Wang Z X,Wang Y Z,Zhang X X,Zhang WX 2012 CoMput.Theor.Chem.993 118
[9]Li S F,Zhao X J,Xu X S,Gao Y F,Zhang Z Y 2013 Phys.Rev.Lett.111 115501
[10]K iMS,Hwang SW,K iMMK,Shin D Y,Shin D H,K iMC O,Yang S B,Park J H,Hwang E,Choi SH,Ko G,SiMS,Sone C,ChoiH J,Bae S,Hong B H 2012 ACS Nano 6 8203
[11]Dah l J E,Liu SG,Carlson R MK 2003 Science 299 96
[12]Yang X B,Zhao Y J,Xu H,Yakobson B I 2011 Phys.Rev.B 83 205314
[13]Sergeeva A P,Popov I A,Piazza Z A,Li WL,RoManescu C,Wang L S,Boldy rev A I 2014 Acc.Chem.Res.47 1349
[14]Xu SG,Zhao Y J,Liao J H,Yang X B 2015 J.Chem.Phys.142 214307
[15]Hartke B 1993 J.Phys.Chem.97 9973
[16]Wang Y C,LüJ,Zhu L,Ma Y M2010 Phys.Rev.B 82 094116
[17]Frontera C,V ives E,Castan T,P lanes A 1995 Phys.Rev.B 51 11369
[18]K resse G,Jurgen H 1993 Phy.Rev.B 47 558
[19]Zhang Y J,X iao X Y,Li Y Q,Yan Y H 2012 Acta Phys.Sin.61 093602(in Chinese)[张英杰,肖绪洋,李永强,颜云辉2012物理学报61 093602]
[20]Liu T D,Li Z P,Ji Q S,Shao G F,Fan T E,Wen Y H 2017 Acta Phys.Sin.66 053601(in Chinese)[刘暾东,李泽鹏,季清爽,邵桂芳,范天娥,文玉华 2017物理学报 66 053601]
[21]Wu L J,Sui Q T,Zhang D,Zhang L,Qi Y 2015 Acta Phys.Sin.64 042102(in Chinese)[吴丽君,随强涛,张多,张林,祁阳2015 物理学报64 042102]
[22]Li P F,Zhang Y G,Lei X L,Pan B C 2013 Acta Phys.Sin.62 143602(in Chinese)[李鹏飞,张艳革,雷雪玲,潘必才2013物理学报62 143602]
[23]LüJ,Wang Y C,Zhu L,Ma Y M2012 J.Chem.Phys.137 084104
[24]Oganov A R,G lass C W2006 J.Chem.Phys.124 244704
[25]Solovyov I A,Solovyov A V,G reiner W,Koshelev A,Shutovich A 2003 Phys.Rev.Lett.90 053401
[26]SWiechoWskiM,Mandziuk J,Ong Y S 2016 IEEE Trans.CoMp.Intel.AI.8 218
[27]V illar S S,BoWden J,Wason J 2015 Stat.Sci.30 199
[28]Sasaki Y,de Garis H 2004 Proceedings of the 2003 Congress on Evolutionary CoMputation Canberra,ACT,Australia,December 8–12,2003 p886
[29]Yang J,Zhang WQ 2007 Acta Phys.Sin.56 4017(in Chinese)[杨炯,张文清 2007物理学报 56 4017]
PACS:36.40.–c,31.15.–p,71.15.PdDOI:10.7498/aps.66.163601
*Project supported by the National Natural Science Foundation of China(G rant No.11474100)and the FundaMental Research Fund for the Central Universities,China(G rant No.2017MS119).
†Corresponding author.E-Mail:scxbyang@scut.edu.cn
Monte-Carlo tree search for stab le structu res of p lanar clusters∗
He Chang-Chun Liao Ji-Hai Yang Xiao-Bao†
(DepartMent of Physics,South China University of Technology,Guangzhou 510640,China)
7 Ap ril 2017;revised Manuscrip t
18 June 2017)
Illustrated by the case of the p lanar clusters,we propose a neWMethod to search the possible stable structures by combining the structural identification and Monte-Carlo tree algorithm.We adopt two kinds of Model-potential to describe the interaction between atoMs:the pair interaction of Lennard-Jones potential and three-body interaction based on the Lennard-Jones potential.Taking the possible triangular lattice fragMent as candidates,we introduce a neWnomenclature to distinguish the structures,which can be used for the rapid congruence check.1)We label the atoMs on the triangu lar lattice according to the distances and the polar angles.where a given triangular structure has a corresponding serial number in the numbered p lane.Note that the congruent structures can have a group of possible serial numbers.2)We consider all the possible symmetrical operations including translation,inversion and rotation,and obtain the sMallest one for the unique noMenclature of the structure.In conventional search ofMagic clusters,the global optiMizations are perforMed for the structures With given number of atoMs.Herein,we perforMthe Monte-Carlo tree search to study the evolution of stab le structures With various numbers of atoMs.FroMthe structures of given number of atoMs,we saMp le the structures according to their energy With the iMportance saMp ling,and then expand the structures to the structures With oneMore atom,where the congruence check With the noMenclature is adop ted to avoid numerous repeated evaluations of candidates.Since the structures various numbers of atoMs are correlated With each other,a searching tree Will be obtained.In order to prevent the over-expansion of branches,we prove the“tree”according to energy to Make the tree asymMetric groWth to retain the loWenergy structure.The Width and dep th of search is balanced by the control of teMperature in the Monte-Carlo tree search.For the candidatesWith lower energies,we further perforMthe localop tiMization to obtain theMore stable structures.Our calculations shoWthat the triangular lattice fragmentsWill bemore stab le under the pair interaction of Lennard-Jones potential,which are in agreement With the previous studies.Under the three body interaction With the specifi c paraMeter,the hexagonal lattice fragMentsWill be More stable,which are siMilar to the configurations of graphene nano-flakes.Combining the congruence check and Monte-Carlo tree search,we provide an eff ective avenue to screen the possible candidatesand obtain the stab le structures in a shorter period of tiMe coMpared With the comMon global op tiMizationsWithout the structural identification,which can be extended to search the stable structure for Materials by the fi rst-princip les calculations.
cluster,structural identification,Monte-Carlo tree,global optiMization
10.7498/aps.66.163601
∗国家自然科学基金(批准号:11474100)和中央高校基本科研业务费(批准号:2017MS119)资助的课题.
†通信作者.E-Mail:scxbyang@scut.edu.cn
©2017中国物理学会C h inese P hysica l Society
http://Wu lixb.iphy.ac.cn
