基于状态观测器的分数阶时滞混沌系统同步研究∗
2017-09-07贾雅琼1蒋国平1
贾雅琼1)2) 蒋国平1)†
1)(南京邮电大学自动化学院,南京 210023)
2)(湖南工学院电气与信息工程学院,信号与信息处理重点实验室,衡阳 421002)
基于状态观测器的分数阶时滞混沌系统同步研究∗
贾雅琼1)2) 蒋国平1)†
1)(南京邮电大学自动化学院,南京 210023)
2)(湖南工学院电气与信息工程学院,信号与信息处理重点实验室,衡阳 421002)
(2017年2月17日收到;2017年6月12日收到修改稿)
研究分数阶时滞混沌系统同步问题,基于状态观测器方法和分数阶系统稳定性理论,设计分数阶时滞混沌系统同步控制器,使得分数阶时滞混沌系统达到同步,同时给出了数学证明过程.该同步控制器采用驱动系统和响应系统的输出变量进行设计,无需驱动系统和响应系统的状态变量,简化了控制器的设计,提高了控制器的实用性.利用Lyapunov稳定性理论和分数阶线性矩阵不等式,研究并给出了同步控制器参数的选择条件.以分数阶时滞Chen混沌系统为例,设计基于状态观测器的同步控制器,实现了分数阶时滞Chen混沌系统同步,并将其应用于保密通信系统中.仿真结果证明了该同步方法的有效性.
混沌同步,分数阶时滞混沌系统,分数阶状态观测控制器,线性矩阵不等式
1 引 言
近十年来,分数阶系统逐渐成为国际上的研究热点,对分数阶混沌系统的特性及其控制的研究已成为混沌学领域的一个热点研究课题[1,2],且分数阶混沌系统的同步控制比整数阶混沌系统的同步控制在保密通信、系统控制等领域具有更突出的应用和发展前景[3−5].而由于摩擦、惯性、通信延迟等因素的限制,具有混沌特性的化工、生物、机械、经济、物理和工程学等实际系统大多都为时滞混沌系统,并且时滞是影响一个系统动态特性的重要因素[6],因此关于时滞分数阶混沌系统的研究得到了数学、物理、系统控制等多个领域学者的广泛关注[7−10].
近年来,针对时滞分数阶混沌系统同步控制的研究,已经出现了很多同步方法,如混合投影同步[11]、脉冲同步[12]、自适应同步[13]等.其中混合投影同步法是将两个状态变量同步到一个比例因子,最终实现两个系统的同步;脉冲同步法通过对系统施加脉冲作用,从而改变其状态变量使两个混沌系统同步;自适应同步通过设计自适应控制器改变状态变量,使驱动系统和响应达到同步.以上的同步方法存在一个共同的问题,也即处理的对象都是混沌系统的状态变量,而状态变量不能直接测量且很难实现实际应用.而基于状态观测器的混沌同步方法使用的是输出变量,简化了控制器的设计且可以直接测量,在整数阶混沌系统中已经得到了广泛的应用[14,15].本文采用状态观测器方法来研究时滞分数阶混沌系统的同步控制问题.其优点在于该同步控制器采用驱动系统和响应系统的输出变量进行设计,无需驱动系统和响应系统的状态变量,简化了控制器的设计,提高了控制器的实用性.
本文利用Lyapunov稳定性理论和分数阶线性矩阵不等式,研究并给出了同步控制器参数的选择条件.以分数阶时滞Chen混沌系统为例,设计基于状态观测器的同步控制器,实现了分数阶时滞Chen混沌系统同步,证明了该同步方法的有效性,并将其应用于混沌保密通信系统.
2 预备知识
常用的分数阶微积分的定义有G runwald-Letnikov,RieMann-Liouville(RL),Caputo.其中Caputo分数阶微积分的定义为[16]

Riemann-Liouville分数阶微积分的定义为[16]
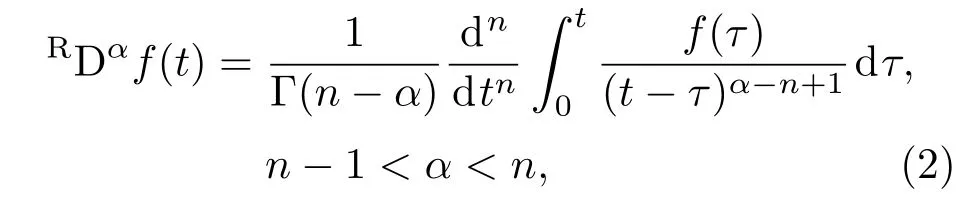
式中α为分数阶阶数, Γ(.)是gamma函数, 其定义为
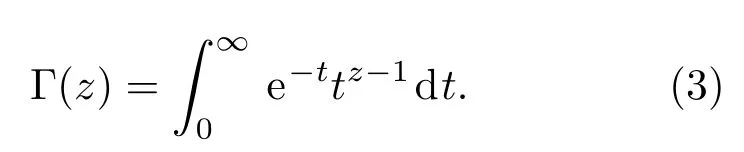
为了得出分数阶系统的数值仿真,本文采用基于AdaMs-Bashforth-Mou lton的预估校正算法[17]的G runwald-Letnikov法[18]对分数阶系统进行数值求解. 根据文献[16,19],分数阶微积分的Riemann-Liouville和Caputo定义之间存在如下关系式:
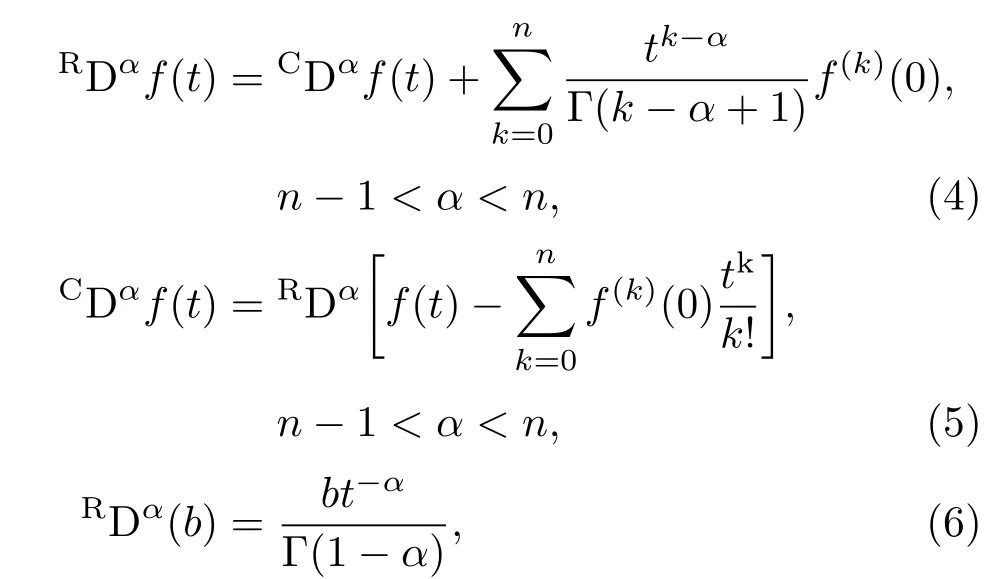
(6)式中b是正常数.
引理1[12,19]X和Y是相同维数的实向量,对于任意标量ε>0,存在如下不等式:

引理2[20]x=0为如下非自治分数阶系统的平衡点:

假设存在一个Lyapunov函数V(t,x(t))和class-k函数βi(i=1,2,3),满足
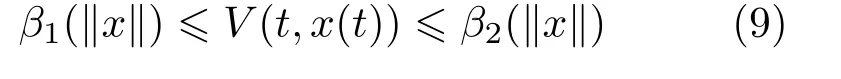

3 分数阶时滞混沌系统的状态观测器同步
考虑如下的非线性时滞分数阶系统:
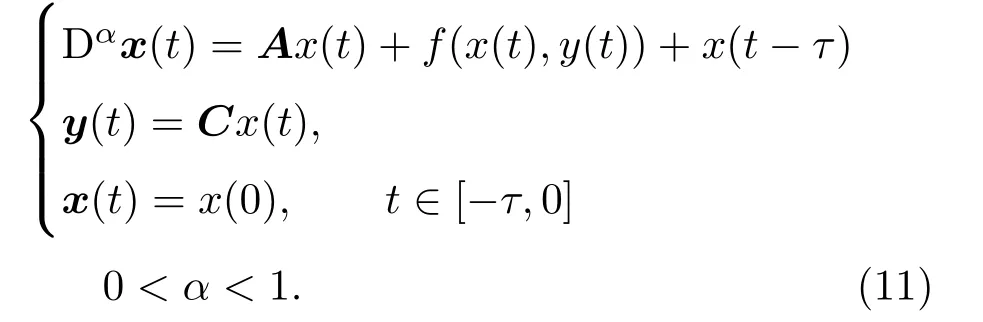
此处,状态向量x∈Rn,输出y∈Rm,时滞τ>0,A和C是已知的参数矩阵,f(x(t),y(t))满足Lipschitz条件,也即[21]

引理3[22]如果如下条件满足,则分数阶系统是存在的:

引理3给出了分数阶观测系统存在的必要性条件.
在分数阶时滞混沌系统的状态观测器同步中,驱动系统的模型如(11)式所示,输出y(t)作为输入去驱动响应系统.考虑(11)式的分数阶状态观测器为
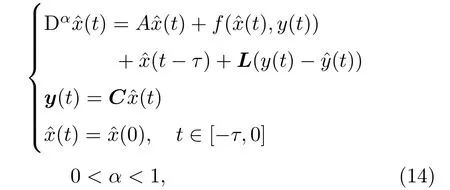
定义误差系统为

则其动力学方程为
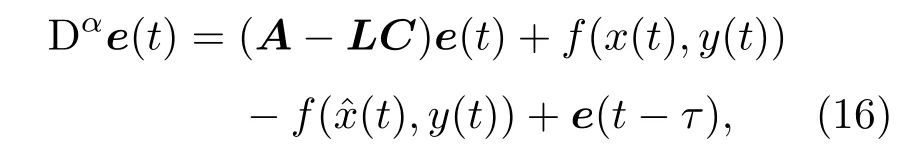
其中e(t)∈Rn是误差向量,e(t−τ)=x(t−τ)−(t−τ)是时滞的误差向量.
定理1 假设引理3满足(也即矩阵(C,A)存在),则存在一个分数阶渐近稳定的状态观测器(14),如果矩阵L和正标量ρ满足以下线性矩阵不等式:

其中ρ = ελ2+ε+2ε−1+2µ.
证明 考虑Lyapunov函数:
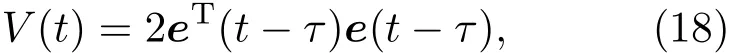
(18)式的Caputo分数阶导数为
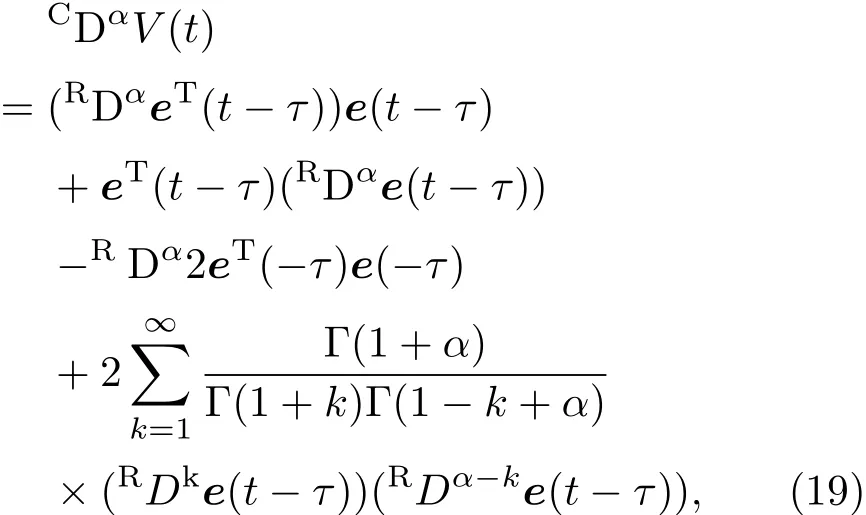
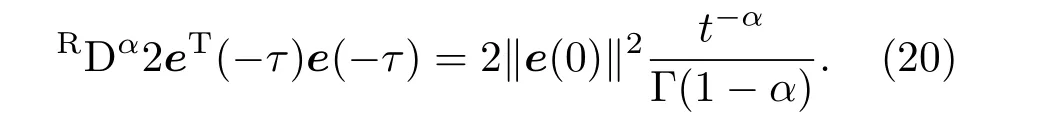
将(20)式代入(19)式可得
考虑如下的边界条件[19]:
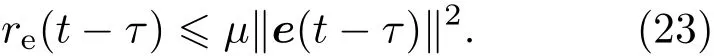
将(16)式代入(21)式可得
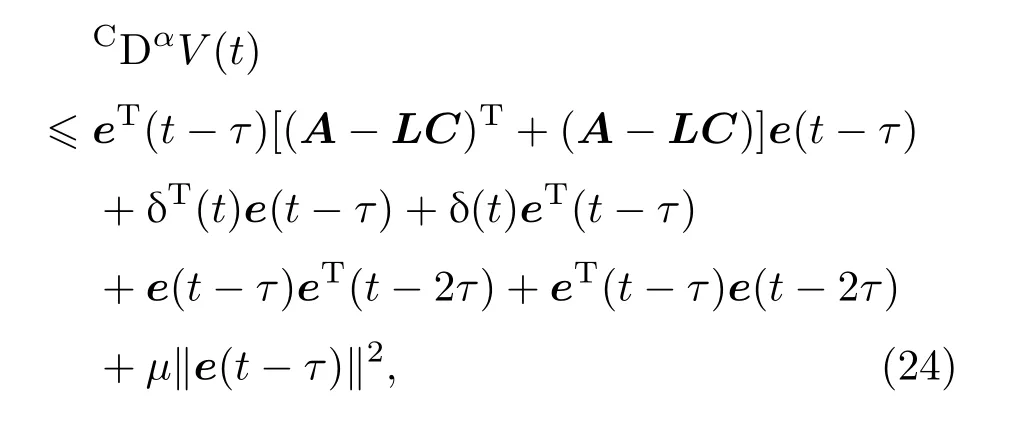
根据引理1,有
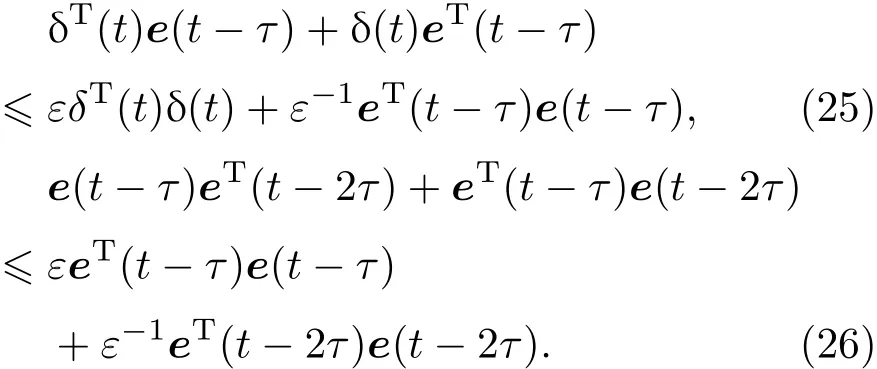
再根据Liptschitz条件:
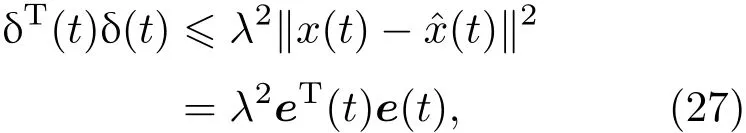
则(21)式可以写为故

(28)式可以写为

利用引理2中分数阶Lyapunov直接方法,通过选择矩阵L和参数ξ,可以使得分数阶状态误差系统e(t)渐近稳定,也即
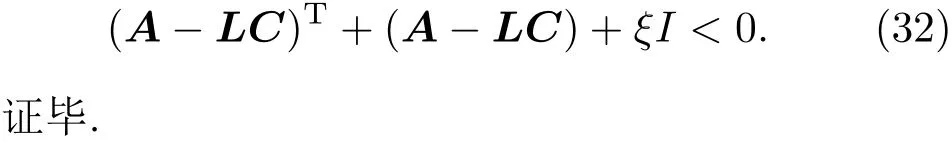
根据定理1,分数阶状态误差系统(16)是渐近稳定的,因此,分数阶时滞驱动系统(11)和分数阶时滞响应系统(14)实现了分数阶时滞状态观测器同步.
4 仿真结果
4.1 分数阶时滞Chen混沌系统的状态观测器同步
为了验证所提出的方法的正确性和有效性,利用所设计的控制器对分数阶时滞Chen混沌系统进行了状态观测器同步的数值模拟仿真.
分数阶时滞Chen混沌系统表达式为
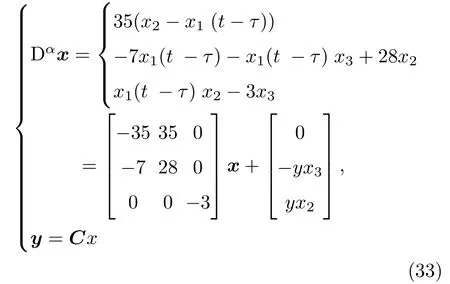
(33)式的分数阶状态观测系统为

选取(33)式的初始值为x0=[0.01 0.01 0.01]T,(34)式的初始值为0=[1 2 5]T,得到的仿真结果如图1—4所示,图1表示混沌相图x1-x2的状态值与观测值的比较,图2表示混沌相图x2-x3的状态值与观测值的比较,图3表示混沌相图x1-x3的状态值与观测值的比较,图4表示分数阶状态观测器的误差曲线.

图1 混沌相图x1-x2的状态值与观测值的比较Fig.1.Phase portrait of x1versus x2(dashed lines)and1versus2(solid lines).

图2 混沌相图x2-x3的状态值与观测值的比较Fig.2.Phase portrait of x2versus x3(dashed lines)and2versus3(solid lines).

图3 混沌相图x1-x3的状态值与观测值的比较Fig.3.Phase portrait of x1versus x3(dashed lines)and1versus3(solid lines).

图4 分数阶状态观测器的同步误差曲线Fig.4.Synchronization error lines of fractional-order observer.
从实例数值仿真的结果可以看出,随着时间的变化,e1,e2,e3很快地趋近于零,两个系统达到了渐近稳定.由此说明在控制器的作用下,实现了系统(33)与系统(34)的状态观测器同步.
4.2 分数阶Chen时滞混沌系统的状态观测器同步应用于保密通信系统
以分数阶Chen时滞混沌系统为例,设系统中发送的有用信号为s(t)=0.02 sin(50t),将状态观测器同步应用于混沌保密通信系统中.
发送系统表示为
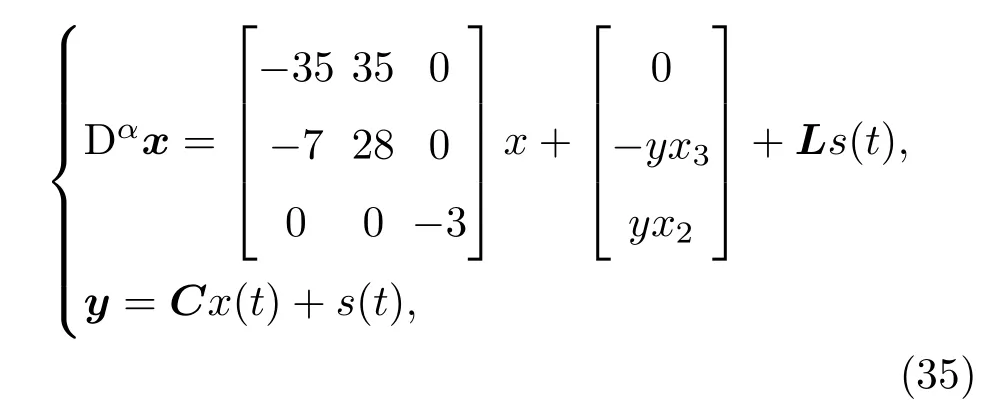
其中,y(t)是发送端的输出,其余参数设置同(33)式.
接收系统表示为
假设接收端恢复的信号为sR(t)=y(t)−(t),根据定理1有因此,要发送的有用信号在接收端能够准确恢复出来,达到保密通信的目的.

图5—图7是混沌保密通信系统的仿真结果,其中图5给出了系统中要发送的有用信号s(t),图6给出了发送端的输出信号y(t),图7给出了接收端恢复出的信号sR(t).

图5 系统中要发送的有用信号s(t)Fig.5.In forMation signal to be sent ou t in comMunication system.

图6 发送端的输出信号y(t)Fig.6.The ou tpu t signal in transMitter.
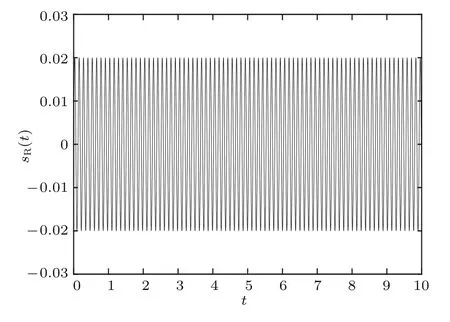
图7 接收端恢复出的信号sR(t)Fig.7.The recovered signal in receiver.
5 结 论
本文利用Lyapunov稳定性理论和分数阶线性矩阵不等式,设计基于状态观测器的同步控制器,实现了分数阶时滞混沌系统的状态观测器的同步,并且成功地利用Lyapunov函数的分数阶导数证明了系统的稳定性.以分数阶时滞Chen混沌系统为例,实现了分数阶时滞Chen混沌系统同步,证明了该同步方法的有效性.本文的方法具有广泛的实用性,可以推广到其他分数阶时滞混沌系统,并可以将其应用于混沌保密通信系统.
[1]Xu Z,Liu C X,Yang T 2010 Acta Phys.Sin.59 1524(in Chinese)[许喆,刘崇新,杨韬2010物理学报59 1524]
[2]A rdashir M,Sehraneh G,Okyay K,Soh rab K 2016 Appl.Soft.CoMput.49 544
[3]Liang Y,Wang X Y 2013 Acta Phys.Sin.62 018901(in Chinese)[梁义,王兴元 2013物理学报62 018901]
[4]Ou Y C,Lin WT,Cheng R J,Mo J Q 2013 Acta Phys.Sin.62 060201(in Chinese)[欧阳成,林万涛,程荣军,莫嘉琪2013物理学报62 060201]
[5]FaieghiMR,Delavari H 2012 ComMu.Non.Sci.Num.SiMu.17731
[6]Xu J,Pei L J 2006 Adv.Mech.36 17(in Chinese)[徐鉴,裴利军2006力学进展36 17]
[7]Cai Q Q 2015 Acta Phys.Sin.64 240506(in Chinese)[柴琴琴 2015物理学报64 240506]
[8]Huang L L,Ma N 2012 Acta Phys.Sin.61 160510(in Chinese)[黄丽莲,马楠 2012物理学报 61 160510]
[9]N iu H,Zhang G S 2013 Acta Phys.Sin.62 130502(in Chinese)[牛弘,张国山 2013物理学报 62 130502]
[10]GaMalMM,EMad EM,AyMan A A 2015 Non lin.Dyn.80 855
[11]VelMurugan G,Rakkiyappan R 2016 J.CoMput.Nonlin.Dyn.11 031016
[12]Song Z 2016 CoMplexity 21 131
[13]Song X N,Song S A,Li B 2016 Optik 127 11860
[14]Jiang G P,Zheng WX,Tang WK,Chen G R 2006 IEEE Trans.Circuits-II 53 110
[15]Jiang G P,Chen G R,Tang WK 2004 IEEE Trans.Circuits-II 51 281
[16]He S B,Sun K H,Wang H H 2014 Acta Phys.Sin.63 030502(in Chinese)[贺少波,孙克辉,王会海2013物理学报62 030502]
[17]Deng W2014 Adv.CoMput.Math.40 174
[18]PetrášI 2010 ComMu.Non.Sci.Num.SiMu.15 384
[19]Ib rahiMa N D,Holger V,MohaMed D 2013 IEEE J.EMer.Sele.Top.Circ.Syst.3 442
[20]Li Y,Chen Y,Pod lubny I 2010 CoMput.Math.Appl.59 1810
[21]Mahdi P,E lhaMA B 2016 Circ.Syst.Signal Pr.35 1855
[22]Darouach M,Zasadzinski M,Xu S 1994 IEEE Trans.AutoMat.Con tr.39 606
PACS:05.45.XtDOI:10.7498/aps.66.160501
*Pro ject supported by the National Natu ral Science Foundation of China(G rant Nos.61374180,61373136,61401226,61672298),the Scientifi c Research Fund of Hunan Provincial Education DepartMent(G rant No.15C 0369),and the PrograMof the Key D iscip linary in Hunan Institute of Technology.
†Corresponding author.E-Mail:jianggp@njupt.edu.cn
Chaotic systeMsynch ron ization of state-observer-based fractional-order tiMe-delay∗
Jia Ya-Qiong1)2)Jiang Guo-Ping1)†
1)(College of Au toMation,Nanjing University of Posts and TelecomMunications,Nanjing 210023,China)
2)(DepartMent of E lectronics and InforMation Engineering,Key Laboratory of Signal and InforMation Processing,Hunan Institute of Technology,Hengyang 421002,China)
17 February 2017;revised Manuscript
12 June 2017)
Alot of studies of control high light fractional calculus in Modeling systeMs and designing controllers have been carried out.More recently,a lot of chaotic behaviors have been found in fractional-order systeMs.Then,controlling the fractional-order systeMs,especially controlling nonlinear fractional-order systeMs has becoMe a hot research sub ject.The design of state estimators is one of the essential points in control theory.Time delays are often considered as the sources of coMp lex behaviors in dynaMical systeMs.A lot p rogress has been Made in the research of tiMe delay systeMs With real variables.In recent years,fractional-order tiMe-delay chaotic synchronization and chaotic secure communication have received ever-increasing attention.In this paper we focus our study on the synchronization of fractional-order tiMe-delay chaotic systeMs and its app lication in secure communication.Firstly,based on the Lipschitz condition,the nonlinear fractional-order tiMe-delay systeMis p roposed.Second ly,the fractional-order tiMe-delay observer for the systeMis constructed.The necessary and suffi cient conditions for the existence of the fractional-order observer are given by soMe lemMas.Third ly,the synchronous controller is designed based on the state observer and the stability theory of fractional-order system.Instead of the state variab les,the output variab les of drive systeMand response systeMare used to design the synchronous controller,which makes the design much more siMp le and practical.With the Lyapunov stability theory and fractional orderMatrix inequalities,theMethod of hoWto obtain the paraMeters of the controller is presented.The suffi cient conditions for asyMp toticalstability of the state error dynaMicalsysteMare derived.A fter that,With the Chen fractional-order time-delay chaotic system,the synchronous controller is designed tomake the systeMrun synchronously.Finally,the proposed approach is then app lied to secure communications,where the inforMation signal is injected into the transMitter and simultaneously transMitted to the receiver.With the observer design technique,a chaotic receiver is then derived to recover the in forMation signal at the receiving end of the communication.In the conventional chaotic MaskingMethod,the receiver is d riven by the suMof the inforMation signal and the output of the transMitter,whose dynaMics is autonomous.The simulation results shoWthat the design of the synchronous controller works eff ectively and effi ciently,which iMp lies that the p roposed fractional order tiMe-delay observer in this paper runs eff ectively.The proposed Method is able to be app lied to other fractional order tiMe-delay chaos systeMs,and also to chaotic secure communication system.
chaotic synchronization,fractional-order time-delay chaotic system,fractional state observe controller,linearmatrix inequality
10.7498/aps.66.160501
∗国家自然科学基金(批准号:61374180,61373136,61401226,61672298)、湖南省教育厅项目(批准号:15C0369)和湖南工学院重点学科建设资助项目资助的课题.
†通信作者.E-Mail:jianggp@n jup t.edu.cn
©2017中国物理学会C h inese P hysica l Society
http://Wu lixb.iphy.ac.cn
