有效质量法调控原子玻色-爱因斯坦凝聚体的双阱动力学∗
2017-09-07刘晓威张可烨
刘晓威 张可烨
(华东师范大学物理与材料科学学院,上海 200062)
有效质量法调控原子玻色-爱因斯坦凝聚体的双阱动力学∗
刘晓威 张可烨†
(华东师范大学物理与材料科学学院,上海 200062)
(2017年4月14日收到;2017年5月12日收到修改稿)
操控原子玻色-爱因斯坦凝聚体在双势阱中的动力学通常是通过改变势阱深度来实现,本文提出了一种基于调节原子有效质量的控制方案,可以在不改变双阱势的前提下操控凝聚体的双阱动力学.利用双模近似,本文解析地导出了超冷原子在双阱势中的隧穿强度和相互作用强度对有效质量的依赖关系,并基于平均场近似数值模拟了在有效质量调节下的凝聚体动力学演化,展示了隧穿振荡和自束缚等典型的双阱动力学行为.此外,本文的研究还发现,借助负有效质量效应,这一方案甚至可以等效地实现对负散射长度原子凝聚体双阱动力学行为的操控.
玻色-爱因斯坦凝聚,双势阱,有效质量
1 引 言
原子的玻色-爱因斯坦凝聚作为一种宏观量子力学效应,一直是物理领域的研究热点之一.其良好的量子相干性使它成为凝聚态物理、非线性物理、量子光学、量子信息与量子计算、精密测量等诸多基础与应用研究领域的共同热点,近年来更是成为了量子物理的研究工具,直接孕育出物质波光学、原子芯片、量子模拟等新的研究方向.在这些研究中,通过电磁场构建各种势场来精密操控原子凝聚体是必不可少的研究手段.例如使用磁场在芯片表面构建原子波导[1,2],利用携带角动量的磁场或光场制备原子团涡旋态[3,4],利用驻波光场作为原子分束器操纵凝聚体实现原子干涉仪或陀螺仪[5−7],或利用驻波光场实现光晶格势来操控凝聚体模拟各种理想的量子多体模型[8−15]等.其中,利用束缚在双阱势场中的原子凝聚体来模拟约瑟夫森超导结效应[16,17]是一个十分典型和基础的量子模拟研究例子.传统的研究方法一般通过操控形成双阱势的磁光场来改变势阱深度,或利用费许巴赫共振法(Feshbach resonance)调节原子的相互作用强度,可以使原子凝聚体展现量子隧穿振荡或自束缚等典型的约瑟夫森结动力学行为[18].
本文提出一种新的凝聚体双阱动力学操控方法,在不改变构成双阱势的磁光场的前提下,通过额外施加一个光晶格势场来调节凝聚体的有效质量,也可以完成动力学操控,使之展示各种典型的双阱量子动力学行为.有效质量理论本来只是一种可以便捷地描述电子、原子等物质波在周期势场中运动的近似理论,但近年来借助飞速发展的光晶格实验技术,原子有效质量已经成为一个可精密调节的物理量,并有希望发展成为一种可以改变原子凝聚体性质的工具.依据光晶格势的参量,原子有效质量可大可小,可以显著地偏离真实原子质量值,导致其动力学性质与量子特性发生显著改变.它甚至可以实现负质量效应,导致凝聚体悬浮[19]、亮孤子凝聚体[20−22]、负温度凝聚体[23]、量子测量反作用消除等[24]一些奇异的物理现象.本文借助平均场近似和数值模拟展示了有效质量法对凝聚体双阱动力学的调控,分析了其内在原因,并讨论了负有效质量情况下凝聚体动力学与负散射长度凝聚体动力学的等效性.
2 系统哈密顿量与有效质量近似
如图1所示,一维对称双阱势场U(x)中囚禁的原子玻色-爱因斯坦凝聚体还受到波矢为kL的驻波光场形成的一维周期势场V(x)=V0cos2(kLx)的操控,系统的完整哈密顿量为

其中M0是原子质量,g=4π2a/M0则代表散射长度为a的原子的碰撞相互作用强度,而(x)是玻色原子场的湮灭算符.双阱势U(x)的具体表达式为

式中参量b与d都是大于√零的实数,该势√阱的两个最低点分别位于x1=处,因此双阱的间距可以表示为D=,而双阱之间的势垒深度为L=.如果光晶格势V(x)的空间变化相对U(x)快得多,并且其势深V0较小不至于使原子凝聚体发生绝缘态相变[14],那我们就可以用慢变包络近似配合有效质量理论来研究原子凝聚体在空间慢变势场U(x)中的运动[19].原子场算符可以用布洛赫函数完备模式来展开


图1 (网刊彩色)装置示意图 原子玻色-爱因斯坦凝聚体除受到一个双阱势(红)束缚外,还额外受到一个细密的可以调节其有效质量的光晶格势(蓝)的影响;双阱的间距和阱间势垒高度分别用D和L表示Fig.1.(color on line)ScheMatic diagraMof setup:The atoMic Bose-Einstein condensate is located in a doub le-well trap(red)With an ex tra fine-grained op tical lattice(b lue)to ad just its eff ectiveMass.The well interval and the barrier height of the doub le-well trap are labelled by D and L,respectively.

式中εn(k)是布洛赫能量,n,k分别标示能带和布洛赫波矢,φn,k(x)满足正交条件

假设凝聚体质心与光晶格势之间的相对运动波矢为k0,则通过布洛赫波函数的慢变包络近似φn,k≈ e i(k−k0)xφn,k0,我们就可以将原子场算符(3)式近似表示为一个中心波矢为k0的空间慢变包络和描述由光晶格引起的快速空间振荡的布洛赫函数的乘积[24],

其中包络场算符

满足玻色场算符对易关系

简便起见,在下文中我们仅考虑原子波被激发到最低能带(即n=1)的情况,因此可以将下标n与k0都省去.将场算符的近似表达式(6)代入系统哈密顿量(1),通过一些计算[见附录A]我们可以得到凝聚体包络场的有效哈密顿量:

其中m∗= ħ2/ε′′(k0)是原子包络场的有效质量,ε′(k0)和 ε′′(k0)分别是第一能带布洛赫能量在波矢k=k0处的一阶和二阶导数.该哈密顿量意味着调节布洛赫能量ε(k)就可以改变原子包络场的有效质量,进而调控凝聚体在双阱势U(x)中的动力学.对布洛赫能量的调节可以通过改变光晶格势深来实现,而k0值的调节则可以通过控制光晶格相对凝聚体质心的移动速度来实现[24].如图2所示,当k0=0或kL时,即在第一布里渊区的中心或边界上,哈密顿量(9)中布洛赫能量的一阶导数项−iε′(k0)∇为零,改变光晶格势的深度V0就可以显著调节有效质量的大小.这种调节甚至可以使有效质量为负,从而导致与正常情况完全相反的动力学行为.为了方便研究有效质量对双阱系统动力学的影响,我们引入参量λ=m∗/M0来代表有效质量与真实质量的比值.

图2 (网刊彩色)(a)原子在光晶格势中的第一布洛赫能带图,布洛赫波矢k0和能量ε(k0)分别以形成光晶格势的驻波光场的波矢kL和原子反冲能量EL=2k2L/2M0为单位;(b)反有效质量比λ−1=M0/m∗随k0的变化.黑色圆圈线,蓝色虚线和红色实线分别对应晶格势深度V0=7EL,4EL,1EL的情况Fig.2.(color on line)(a)The fi rst-band B loch energy for the atoMs trapped in the op tical lattice With the B loch wave vector k0;(b)the inverted eff ective Mass ratio,λ−1=M0/m∗,as a function of k0,the b lack circle,the b lue dashed curves and the red solid curves are for the cases of lattice dep th V0=7EL,4EL,1EL,respectively.the B loch wave vector and the energy are norMalized by the wave vector of the op tical lattice kLand the atoMic recoil energy EL=ħ2k2L/2M0,respectively.
3 双阱动力学调控
以下我们展示有效质量对凝聚体在双阱势中动力学行为的调控.对于一维双势阱U(x),当势阱较深时我们可以采用双模近似,构建左右阱的局域波函数来近似描绘凝聚体的运动[10].包络场算符可表示成两个局域模的叠加形式:


式中Ω代表原子在双阱之间的遂穿率,而κ代表同一阱中原子的碰撞率.为了便于比较,我们引入未经有效质量调控时(即λ=1时)的双阱隧穿率Ω0=exp(−d/2b)以及相互作用率κ0=作为参考值,g′代表一维有效原子相互作用强度,则有关系

其中正负号取决于有效质量比λ的符号,即有效质量的正负.方程(12)和(13)说明可以通过调控有效质量来改变隧穿率和碰撞率.我们先考虑有效质量为正的一般情况,为负的情况将在本文末尾讨论.
为了对凝聚体的动力学演化做数值模拟,我们根据一些典型的实验参数来估计隧穿率和碰撞率的取值.以磁光阱束缚的碱金属原子凝聚体为例,实验中双阱间距D的尺度可在1—100µm之间调节,而光晶格势的每个格点尺度则在约0.1µm量级,完全可以满足之前我们对晶格势空间变化率远大于双阱势的假设.按照文献[26]中的实验数据,双阱宽度D=13µm,势垒深度L=h×4.7 kHz(h为普朗克常数),对应d=h×2.2×1014Hz/m2和b=h×2.6×1025Hz/m4.以87Rb原子为例,单原子质量M0=87×1.7×10−27kg,原子s波散射长度a=5.7 nm[27],由此可估算出原始遂穿率Ω0=2π×28.2 kHz,碰撞率κ0=2π×0.5 Hz.如图3所示,在固定双阱势参量的情况下,凝聚体隧穿率Ω和碰撞率κ随有效质量的改变展示出相反的变化趋势.以无光晶格调控有效质量时的值为参考,碰撞率随有效质量的增大而增大,而隧穿强度则变小.这也符合量子特征随质量增加而减弱这一通常的规律.

图3 原子遂穿率Ω (实线)和相互作用率κ(虚线)随着有效质量比λ的变化,计算所使用的双阱势和原子参数详见正文Fig.3.The atoMic tunneling rateΩ(solid line)and the interaction rateκ(dashed line)as functions of the eff ective Mass ratioλ.See the Main tex t for the detailed paraMeters used in the calculation.
在总原子数较大且碰撞相互作用较弱的情况下,我们可以安全地忽略所有的量子涨落和量子关联效应,用平均场近似理论来描述双阱系统的动力学[28].将原子产生湮灭算符用它们的平均值代替,L(R)≈L(R)〉=e iϕL(R)(t),式中N L(R)和ϕL(R)分别代表左(右)阱中原子的平均布居数和相位,再代入(11)式中就可以获得描述双阱系统的经典哈密顿量.如果进一步定义两个新的自由度,双阱之间的相位差ϕ=ϕL−ϕR和归一化的原子布居差ρ=(NL−NR)/N取值范围分别为[−π,π]和[−1,1],则经典哈密顿量简化为

其中,EJ=EJ0exp(−(− 1)d/2b)和Es=Es0λ1/4分别代表受有效质量调控的隧穿和相互作用能量,而EJ0= ħΩ0N/4和Es0= ħκ0N2/2则分别对应未受调控时的值.原子凝聚体的良好相干性使我们可以在短时间(约1 s量级)内安全地忽略各种损耗效应,通过哈密顿正则方程来描述体系的动力学,

该方程组说明双阱动力学演化对应一个摆角为ϕ、摆幅为ρ、并且摆长非线性变化的经典单摆.很容易发现它有两个不依赖于隧穿能量EJ和相互作用能Es的稳态解,{ρ =0,ϕ =0}和{ρ=0,ϕ = π},对应左右阱原子数和相位完全相同或原子数相同而相位完全相反.除了这两个平庸稳态之外,当相互作用能较大时,即|Es|>EJ,它还有两组原子数非对称的稳态解,{ρ2=1−E2J/E2s,ϕ =0,π},其中ϕ=0对应Es<0的情况而ϕ=π对应Es>0.而系统的动力学特征则取决于相互作用能量与隧穿能量的比值Es/EJ以及系统的初始条件ρ(0)和ϕ(0)的选取,可分为简谐振荡、非谐振荡、自束缚等一些类型[28].通常的双阱动力学操控是通过调节外场以改变双阱势U(x)的形状[29],或者通过费许巴赫共振法调节原子间的散射长度以改变相互作用强度来实现[30],最终都落实到改变Es0/EJ0的比值上.而现在我们可以通过光晶格势来操纵凝聚体的有效质量,即改变λ,同样也可以实现对Es/EJ的值以及对应的双阱动力学的操控.

图4 (网刊彩色)有效质量比为(a)λ=1,(b)λ=0.1,(c)λ=1.28,(d)λ=10情况下左右阱中原子凝聚体的归一化粒子数差ρ(蓝色实线)和相位差ϕ(红色虚线)随时间的演化,时间单位为ħ/EJ0 (e),(f),(g),(h)是与(a),(b),(c),(d)对应的在{ρ,ϕ}相空间中的能量等高图,如标尺所示颜色越深能量越低,能量值以EJ0为单位;所有情况下原子凝聚体的初始条件相同(ρ(0)=0.55,ϕ(0)=0,对应能量图中的白点)双阱势U(x)也相同,其余参量与图3一致Fig.4.(color on line)Left coluMn:The tiMe evolu tion of the popu lation diff erenceρ(b lue solid lines)and the phase diff erence ϕ(red dashed lines)of the atoMic condensate in the doub le-well trap With diff erent eff ective Mass ratios(a)λ=1,(b)λ=0.1,(c)λ=1.28,(d)λ=10.The initial cond itions for all the cases areρ(0)=0.55 andϕ(0)=0 and the paraMeters of the trap potential are the saMe as Fig.3.Right coluMn:The energy contou r p lots of the systeMin space of{ρ,ϕ}With lower energy labeled in deeper color.(e),(f),(g),and(h)correspond to the HaMiltonian of(a),(b),(c),and(d),respectively.The comMon initial cond itions are Marked by the White points.The tiMe and the energy are norMalized by h/EJ0and EJ0,respectively.
在图4中我们通过模拟动力学方程(15)在同一初始条件但不同λ值下的演化,来展示有效质量法对双阱中凝聚体动力学的调控.此外我们还通过分析有效质量比λ对哈密顿量(14)的影响来分析动力学发生显著改变的原因.图4的左列与右列分别展示了系统在同一初始条件但不同有效质量情况下,左右阱粒子数差ρ与相位差ϕ随时间的演化和哈密顿量即系统总能量在{ρ,ϕ}参量空间的等高图.由于忽略了所有的损耗效应,系统在演化过程中总能量守恒,所以其瞬时状态点{ρ(t),ϕ(t)}始终位于初态(ρ=0.55,ϕ=0)对应能量值所在的等高线上.然而当有效质量改变引起隧穿率和碰撞率变换时,能量等高线结构本身会发生对应的扭曲变形,导致系统动力学发生显著的改变.当没有用有效质量法调控时,即图4(a)和图4(e)中λ=1的情况,凝聚体初态所在的能量等高线呈一个两头尖的橄榄形,状态点沿这一形状运动时,ρ展现出三角波形的非谐振荡,而ϕ则为简谐振荡.当有效质量比λ=0.1时,即有效质量远小于真实质量,按照前文的分析隧穿率将会被放大而碰撞率变小,其能量等高线变为一个规则的椭圆,如图4(f)所示.状态点沿这一椭圆运动时,ρ与ϕ对应的动力学演化是振幅不同但周期相同的简谐振荡,如图4(b)所示.而当λ=1.28时,有效质量大于真实质量,情况则相反,碰撞增强而隧穿减弱,原来橄榄形的能量等高线在尖端处进一步扭曲.此时ϕ的运动变为近似矩形波的非谐振荡,而ρ的运动则在振荡之间展示出奇异的平坦段,这对应着非线性单摆的临界减慢效应[31].随着有效质量进一步变大,非线性效应显著地增强.当λ=10时,能量等高线趋向平直,ϕ的运动变成了高度非谐的锯齿波振荡,而ρ则不再振荡意味着左右阱原子数不同但差值固定,这对应着由高度非线性引起的自束缚效应[32].
4 负质量情况
费许巴赫共振法不但可以调节原子相互作用强度g的大小,还可以改变其正负使相互作用由排斥变为吸引,从而使得双阱系统的动力学发生显著改变.有效质量法虽然不能直接改变原子间的相互作用性质,但却可以利用负质量物体的力学响应与正质量物体完全相反这一特性,实现与改变原子相互作用性质等效的操控.
当有效质量为负时,势能最高处才是凝聚体运动的基态所在,因此只要完全翻转双阱势,即将哈密顿量(1)中的U(x)变为−U(x),就仍可以采用双模近似来描述凝聚体的动力学,所获得的动力学方程组如下:

与方程组(15)相比只是隧穿能量EJ的值变为负数.而另一方面,当原子质量为正而相互作用为吸引时,其动力学方程的改变则体现在Es值变负,


比较这两种情况下的动力学方程组不难发现,只要将负质量动力学方程组中的ρ变为−ρ而ϕ不变,或者将ϕ变为−ϕ而ρ不变,就可以使两组方程完全一致.因此,当凝聚体的有效质量为负而原子相互作用为正时,只要完全翻转双阱势,并在制备系统初态时注意将原子数差ρ的定义中的左右顺序反过来或赋予相位差ϕ一个额外的π相移,就完全可以模拟质量为正而相互作用为负的原子凝聚体在双阱势中的动力学行为.
5 结 论
本文提出了通过光晶格调节原子凝聚体有效质量,从而控制凝聚体在双阱势中的动力学行为的方案.借助双模近似与平均场近似,我们导出了双阱中凝聚体的隧穿率与原子相互作用率对有效质量值的依赖关系,并通过数值模拟展示了有效质量发生改变时,凝聚体在双阱中的动力学行为由量子隧穿占主导的简谐振荡到原子碰撞占主导的自束缚的转变.此外,我们还指出通过使有效质量变负的方法可以模拟吸引型原子相互作用的凝聚体的双阱动力学.与直接调整形成双阱势的磁光场或用费许巴赫共振法调节原子相互作用的传统方案不同,本文的方案不改变原有束缚场而是通过额外施加一个驻波光场来实现,对一些要求固定外场束缚条件的原子凝聚体应用研究或是对磁场调节不敏感的原子较有意义.此外尽管我们只分析了外场是双阱势的情况,但只要这些束缚势的空间变化率远小于用来调节有效质量的光晶格势,该方案对其他形状的束缚势同样有效.未来我们希望将有效质量法进一步拓展到对凝聚体原子量子多体动力学与量子关联的操控上.
附录A 包络场哈密顿量(8)的导出

式中,V(x)是光晶格势,U(x)是双阱势场,M0是原子真实质量.对布洛赫函数φk(x)进行慢变包络近似后,原子场算符(x)可近似表示为


k是准动量波矢,而k0代表BEC的质心动量波矢,k是原子在布洛赫模式上的湮灭算符,满足玻色对易关系.为简便起见我们只讨论第一布洛赫能带的情况.包络场算符(x)与k间有傅里叶逆变换关系,
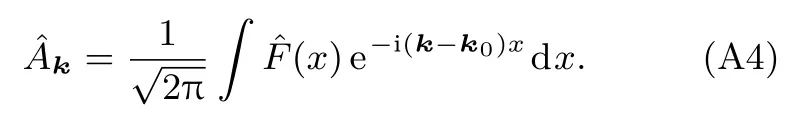


其中有效质量m∗=


[1]H inds E A,Boshier MG,Hughes IG 1998 Phys.Rev.Lett.80 645
[2]ThyWissen J H,O lshaniiM,ZaboWG,D rnd ic M,Johnson K S,Westervelt R M,Prentiss M1999 Eur.Phys.J.D 7 361
[3]Andersen MF,Ryu C,C ladéP,Natara jan V,Vaziri A,HelMeison K,Phillips WD 2006 Phys.Rev.Lett.97 170406
[4]Du tton Z,Ruostekoski J 2004 Phys.Rev.Lett.93 193602
[5]G iltner D M,McGowan R W,Lee S A 1995 Phys.Rev.Lett.75 2638
[6]Gustavson T L,Bouyer P,Kasevich MA 1997 Phys.Rev.Lett.78 2406
[7]Stringari S 2001 Phys.Rev.Lett.86 4725
[8]Densch lag J H,SiMsarian J E,Häff ner H,McKenzie C,B rowaeys A,Cho D,HelMerson K,Rolston S L,Phillips WD 2002 J.Phys.B:At.Mo l.Opt.Phys.35 3095
[9]Choi D,Niu Q 1999 Phys.Rev.Lett.82 2022
[10]Milburn G J,Corney J,Wright E M,Walls D F 1997 Phys.Rev.A 55 4318
[11]Bu rger S,Cataliotti F S,Fort C,Minardi F,Inguscio M,Chiofalo ML,Tosi MP 2001 Phys.Rev.Lett.86 4447
[12]Xu Z J,Cheng C,Yang H S,Wu Q,X iong H W2004 Acta Phys.Sin.53 2835(in Chinese)[徐志君,程成,杨欢耸,武强,熊宏伟2004物理学报53 2835]
[13]Q i R,Yu X L,Li Z B,Liu WM2009 Phys.Rev.Lett.102 185301
[14]Jaksch D,Bruder C,Cirac J I,Gard iner C W,Zoller P 1998 Phys.Rev.Lett.81 3108
[15]G reiner M,Mandel O,Esslinger T,Hänsch T W,B loch I 2001 Nature 415 39
[16]Ji A C,Sun Q,X ie X C,Liu WM2009 Phys.Rev.Lett.102 023602
[17]Liu WM,Fan WB,Zheng WM,Liang J Q,Chui S T 2002 Phys.Rev.Lett.88 170408
[18]SMerzi A,Fantoni S,G iovanazz S,Shenoy S R 1997 Phys.Rev.Lett.79 4950
[19]Pu H,BaksMaty L O,Zhang W,BigeloWN P,Meystre P 2003 Phys.Rev.A 67 043605
[20]Strecker K E,Partridge G B,Truscott A G,Hu let R G 2002 Nature 417 150
[21]He ZM,Wang D L,D ing JW,Yan X H 2012 Acta Phys.Sin.61 230508(in Chinese)[何章明,王登龙,丁建文,颜晓红2012物理学报61 230508]
[22]He Z M,Wang D L 2007 Acta Phys.Sin.56 3088(in Chinese)[何章明,王登龙 2007物理学报 56 3088]
[23]Mosk A P 2005 Phys.Rev.Lett.95 040403
[24]Zhang K Y,Meystre P,Zhang WP 2013 Phys.Rev.A 88 043632
[25]Ananikian D,BergeMan T 2006 Phys.Rev.A 73 013604
[26]Shin Y,Saba M,Pasquini T A,K etterle W,Pritchard D E,Leanhard t A E 2004 Phys.Rev.Lett.92 050405
[27]Dalfovo F,G iorgini S,Pitaevskii L P,Stringari S 1999 Rev.Mod.Phys.71 463
[28]Raghavan S,SMerzi A,Fantoni S,Shenoy S R 1999 Phys.Rev.A 59 620
[29]Michael A,Gati R,Fölling J,HunsMann S,CristianiM,Oberthaler MK 2005 Phys.Rev.Lett.95 010402
[30]Spagnolli G,SeMeghini G,Masi L,Ferioli G,Trenkwalder A,Coop S,Land ini M,PezzéL,Modugno G,Inguscio M,SMerzi A,Fattori M2017 arxiv 1703.02370[quant-ph]
[31]Gati R,Oberthaler MK 2007 J.Phys.B:At.Mol.Opt.Phys.40 R 61
[32]Jack MW,Collett MJ,Walls D F 1996 Phys.Rev.A 54 R 4625
PACS:03.75.Kk,05.30.Jp,03.75.lm,67.85.JkDOI:10.7498/aps.66.160301
*Pro ject supported by the National Natu ral Science Foundation of China(G rant Nos.11574086,91436211,11234003),the National Key Research and DevelopMent PrograMof China(G rant No.2016YFA 0302001),the Ma jor Research P lan of the National Natural Science Foundation of China(G rant No.11654005),and the Shanghai Rising-Star Program,China(G rant No.16QA 1401600).
†Corresponding author.E-Mail:kyzhang@phy.ecnu.edu.cn
E ff ective-Mass app roach to controlling doub le-Well dynaMics of atoMic Bose-Einstein condensates∗
Liu Xiao-Wei Zhang Ke-Ye†
(DepartMent of Physics and Material Science,East China NorMal University,Shanghai 200062,China)
14 Ap ril 2017;revised Manuscrip t
12 May 2017)
The realization of Bose-Einstein condensation in dilute atoMic gases opens an exciting way to quantuMMechanics and begins a neWarea of quantuMsimu lation.As aMacroscopic quantuMob ject and aMany-body bosonic system,the Bose-Einstein condensates can shoWnumerous exotic quantuMeff ects and have naturally attracted great attention.One of the siMp lest quantuMMany-body systeMs to be realized experiMentally and studied theoretically is u ltra-cold atoMs in a doub le-well potential.This systeMcan exhibit a great variety of quantuMinterference phenoMena such as tunneling oscillation,self-trapping and the entanglement of macroscopic superpositions.Specifically,the double-well potentials built by optical or Magnetic fields are easy to change and theMany-body interaction between ultra-cold atoMs can be changed by themethod of Feshbach resonance,enabling the precise quantuMcontrol of the double-well dynaMics of the condensates.
In the present work,we study the dynaMics of a condensate in Atrapping potential consisting of an unalterable double-well trap and an additionalmoving optical lattice.If the lattice space ismuch smaller than the size of the doublewell trap,the systeMcan be siMp lified into a double-well trapped condensate With Atunable eff ectiveMass.Using the Mean-field factorization assuMption,together With Atwo-Mode approxiMation,we obtain the analytic exp ressions for the dependence of the tunneling rate and the self-collision strength on the eff ectivemass.The tunneling rate decays and the collision strength groWs up With the increase of the eff ectiveMass.As a consequence of their diff erent changes,we conclude that the ad justMent of the eff ectiveMass of the ultra-cold atoMs,rather than the changing of the trap barrier or ad justing of the atoMic scattering length,is an alternative approach to controlling the double-well dynaMics of the condensate.V ia nuMerical simulations of the Mean-field dynaMical equations With soMe realistic paraMeters,we shoWthat Atransition between the quantuMcoherent tunneling and the self-trapping behaviors is experimentally realizable With the Mass-control approach.Specifi cally,we shoWthat the app roach is still valid for the case of negative Mass.Moreover,we find that the negative-Mass case can be used even to stimulate the doub le-well dynaMics of the condensate With a negative atoMic scattering length.
Bose-Einstein condensation,doublewell,eff ectivemass
10.7498/aps.66.160301
∗国家自然科学基金(批准号:11574086,91436211,11234003)、国家重点研发计划(批准号:2016YFA 0302001)、国家自然科学基金委应急管理项目(批准号:11654005)和上海市启明星人才计划(批准号:16QA 1401600)资助的课题.
†通信作者.E-Mail:kyzhang@phy.ecnu.edu.cn
©2017中国物理学会C h inese P hysica l Society
http://Wu lixb.iphy.ac.cn
