一道数学问题解法的自然生成及其教学启示

韩龙淑，郝晓鑫

（太原师范学院数学系）

一道数学问题解法的自然生成及其教学启示

韩龙淑，郝晓鑫

（太原师范学院数学系）

数学解题的思路和方法力求简单自然.以一道数学问题为例，在题目的思路分析与解法展示基础上进行解题反思.提出善于运用启发性提示语合乎情理地探索解题思路的自然生成；借助分割拼补图形与类比构造辅助问题，探寻解题思路的通法并学会一题多变；通过“少算多思”进行整体求解，提升学生的思维层次和思维品质.

数学问题；解题反思；自然生成；少算多思

探寻简单自然的方法是数学解题追求的基本要义.善于把未解决或不易解决的问题化归为已解决或易解决的问题是数学解题常用的思维方式和思考方法.正如波利亚所指出的：当原来的问题看起来似乎不好解时，就构想一个合适的辅助问题.而运用分割拼补图形与类比的思想方法，构建与所求图形面积有实质联系的特殊辅助图形是求面积问题自然生成的化归路径.

一、题目呈现

题目 数学活动——求重叠部分面积.

问题情境：数学活动课上，教师出示了一个问题.

如图1，将两块全等的直角三角形纸片△ABC和△DEF叠放在一起，其中∠ACB=∠E=90°，BC=DE=6，AC=FE=8，顶点D与边AB的中点重合，DE经过点C，DF交AC于点G.求重叠部分（△DCG）的面积.

（1）独立思考：试解答教师提出的问题.

（2）合作交流：“希望”小组受此问题的启发，将△DEF绕点D旋转，使DE⊥AB交AC于点H，DF交AC于点G，如图2，你能求出重叠部分（△DGH）的面积吗？试写出解答过程.

（3）提出问题：教师要求各小组向“希望”小组学习，将△DEF绕点D旋转，再提出一个求重叠部分面积的问题.“爱心”小组提出的问题是：如图3，将△DEF绕点D旋转，DE，DF分别交AC于点M，N，使DM=MN，求重叠部分（△DMN）的面积.

任务：①试解决“爱心”小组所提出的问题，直接写出△DMN的面积是______.

②试仿照以上两个小组，大胆提出一个符合教师要求的问题，并在图中画出图形，标明字母，不必解答（注：也可在图1的基础上按顺时针方向旋转）.

图1

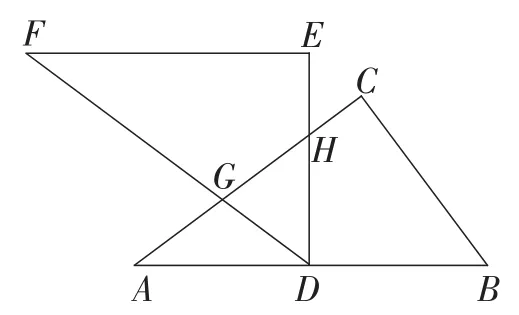
图2

图3

二、题目的思路分析与解法展示

1.第（1）小题的思路分析与解法展示

如图1，要求△DCG的面积，DC为Rt△ABC斜边上的中线可求，但DC边上的高不易入手求解.由于Rt△ABC的面积易求，而△DCG为Rt△ABC的一部分，因此需要进一步寻找△DCG与△ABC之间的联系，自然先从与二者有直接联系的特殊公共点D入手，探求△DCG是否有特殊性质呢？D为AB的中点，△ABC为直角三角形，由直角三角形斜边上的中线等于斜边的一半的性质，得DB=DC，∠BCD=∠B.而△ABC和△DEF全等，有∠CDG=∠B.所以∠CDG=∠BCD.可知DG∥CB.因此，∠CGD=90°，△DCG为直角三角形，且G为AC的中点.则GC=4，GD=3.所以S△CGD=6.

2.第（2）小题的思路分析与解法展示

如图2，要求△GDH的面积，发现其不是直角三角形，则与△ABC不相似.△GDH虽然为△ABC的一部分，但它们的顶点无公共点，面积比例关系难寻.能否寻找与△GDH有一个公共顶点且与△ABC相似的直角三角形，使△GDH成为该直角三角形的一部分呢？

从已知条件入手，看能得出什么新的信息.已知ED⊥AB，则∠EDA=90°.因此，Rt△ADH包含△GDH且与△ABC含有公共∠A，从而△ADH与△ABC相似.有. 推出 S△ADH∶ S△ABC=25∶64. 因此 S△ADH可知.Rt△ADH自然成为所找的辅助直角三角形.

此时需进一步寻找S△GDH与S△ADH的关系.经分析由ED⊥AB，FE⊥ED，可得FE∥AD.所以∠F=∠ADG.而∠A=∠F，则∠ADG=∠A.所以AG=GD.而∠A+∠GHD=90°， ∠ADG+ ∠GDH=90°， 故 ∠GHD=∠GDH.所以GD=GH.因此AG=GH.所以G为AH的中点，则 S△GDH∶ S△ADH=1∶2， S△GDH∶ S△ABC=25∶128.而 S△ABC=24 ，则.

3.第（3）小题中①的思路分析与解法展示

如图3，要求等腰三角形DMN的面积，但△DMN与△ABC不相似，比例关系不易获得.类比第（2）小题的思路受到启发，通过拼、补寻找与△DMN有一公共顶点且与△ABC相似的直角三角形，并使△DMN成为该直角三角形的一部分.

但已有△ADM不是直角三角形，尝试构造满足条件的直角三角形.而点D既为△DMN的顶点，又为△ABC边BC的中点，自然想到连接CD，构造△CDN.若∠CDN=90°，则△CDN可作为辅助的桥梁三角形.类比第（2）小题的方法，由MN=MD，得∠MND=∠MDN.而∠MDN=∠B=∠DCB，故∠MND=∠DCB.因为∠BCD+ ∠DCN=90°，所以∠MND+ ∠DCN=90°，∠CDN=90°. 从而△CDN为包含△DMN的辅助直角三角形.

由于△CDN与△ABC为含有等角∠CND与∠B的直角三角形，故它们相似.因此由CD∶AC=5∶8，可得S△CDN∶ S△ABC=25∶64. 再看 S△MDN与 S△CDN的比例，发现两三角形有一底边共线，故注意指向寻找MN与MC的长度关系.与第（2）小题的思路类似，因为∠MND+ ∠DCN=90°，∠MDN+ ∠MDC=90°，得出∠MDC=∠DCN.从而MN=MD=MC，即M为CN的中点. 故S△DMN∶S△CDN=1∶2.所以S△DMN∶S△ABC=25∶128.故.

三、解题反思与教学启示

1.善于运用启发性提示语合乎情理地探索解题思路的自然生成

波利亚在《怎样解题》中给出了一系列启发性提示语，对数学解题思路的探索和方法的自然生成具有重要的引导作用.此题中探索解题思路时运用启发性提示语：要求什么？（△DCG的面积）.已知数据和条件有哪些？（Rt△ABC的面积可求，DC为Rt△ABC斜边上的中线也可知）.还需求什么？（DC边上的高）.但把DC作为△DCG的底边后，DC边上的高不易求得，至此思维受阻.教师可继续运用启发性提示语顺乎自然地帮助学生：当DC边上的高看起来似乎不好解时，能否寻找△DCG与△ABC中角的关系？能从已知数据中再得到一些有用的信息吗？启发学生从角方面进一步思考，由直角三角形斜边上的中线的性质，得DB=DC，∠BCD=∠B.而∠CDG=∠B，所以∠CDG=∠BCD.可知DG∥CB.因此∠CGD=90°，G为AC的中点.从而△DCG的面积可求.

运用启发性提示语旨在使学生经历解题中自然而然的数学思考过程，体验思维过程展开的自然和思考方法生成的自然，以此感悟数学解题思路和思维方法的自然生成，从而积累数学解题的实践活动经验和思维活动经验.运用启发性提示语最终要使学生学会自我启发，逐步提炼具有自身认知风格的提示语，从而学会数学思考.

2.借助分割拼补与类比构造辅助问题，探寻解题思路的通法，并学会一题多变

当原来的问题看起来似乎不好解时，就需要想出一个合适的辅助问题，构造辅助问题是重要的思维活动.通过反思上述三个问题的共同思路发现，借助分解拼补图形与类比，构建与所求图形面积有实质联系且与母三角形相似的辅助直角三角形（已知与未知的中间桥梁）是求该面积问题自然生成的化归路径，即要求的三角形面积均为辅助直角三角形面积的一部分，使所求三角形与易求面积的辅助直角三角形建立联系，且这些辅助直角三角形与△ABC相似，面积易求，从而原三角形面积可求.第（1）小题中所求△DCG的面积本身为直角三角形的面积；第（2）小题中寻找与△ABC相似的辅助Rt△ADH，并将要求面积的△GDH分割为辅助Rt△ADH的一部分；第（3）小题中类比第（2）小题的思路，通过连接CD拼补出与Rt△ABC相似且包含所求△DMN的辅助Rt△CDN，从而求得原△DMN的面积，由此可见特殊的辅助图形“直角三角形”具有广阔的拓展空间.

在解题时，若学生具有将一般三角形与特殊的辅助直角三角形建立自然的、内在联系的意识，抓住问题的本质，便可突破植根于基本辅助图形“直角三角形”的大量题目.学生有了反思解题的思维过程和思考方法的习惯后，自然地可继续发现提出新问题.由此研究第（3）小题中的问题②.

前面问题中都是△DEF绕点D逆时针方向旋转，分别使DF⊥AC，DE⊥AB，DM=MN，由此自然发现新问题：△DEF绕点D顺时针方向旋转如何呢？从而自然提出新问题：如图4，△DEF绕点D顺时针方向旋转，使DE⊥BC交于点M，DF交AC于点N.如何求重叠部分（四边形DMCN）的面积呢？自然类比解前三个问题的通法，四边形DMCN的面积可化归为△ABC的面积减去与母三角形相似的两直角三角形AND和直角三角形DMB的面积，重叠部分四边形DMCN的面积同样可求.

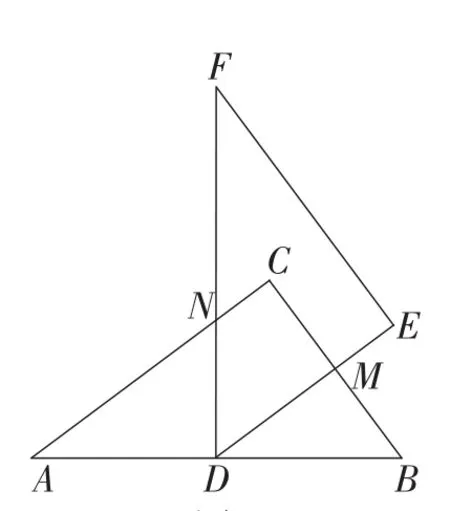
图4

数学学习离不开解题，而数学题终身解不完，需要获得手边题目中那些对解后来题目有用的特征，以此设法揭示出隐藏在眼前具体情形中的一般模型，以此彰显提出数学问题、解决数学问题和拓展数学问题的自然.通过一法多思，即直接求图形面积不易时，可构造与基本图形相似且与所求图形有内在联系的、易求面积的特殊辅助图形.并在分析和解决问题的过程中不断发现、提出有意义的新问题，从而实现一题多变.使数学解题成为学生“分析、解决问题—发现、提出新问题—再分析、解决问题—再发现、提出新问题……”的循环“四能”链.重在使学生通过一个或几个问题的解决获得解决一类问题的通法，从而由数学母题形成数学题链，乃至数学题网，最终提高学生数学解题的收益率.

3.通过“少算多思”进行整体求解，提升学生的思维层次和思维品质

继续反思上述问题中探寻解题自然路径的通法，直接求解原三角形面积不易时，关键在于构造与所求图形面积有内在联系的辅助直角三角形，而辅助直角三角形与母三角形相似，因此面积之比等于相似比的平方，从而不需要分别求辅助三角形的底和高（如第（2）小题中的Rt△ADH，第（3）小题中的问题①的Rt△CDN，第（3）小题中的问题②的Rt△AND和Rt△DMB），就可直接通过面积之比的整体求解来获得辅助图形的面积，以此大大简化运算，避免学生陷入思维在同一层次、低水平重复的单一运算中，并克服求三角形面积时需要分别求出底和对应高的思维定势.通过“少算多思”进行整体求解，体现了运算方法与步骤的自然性和简洁性.由于运算简单的解题方法，往往要求有较高的思维品质，因此通过“少算多思”简化数学运算，有利于提升学生数学解题的思维强度和思维层次，从而完善数学思维品质.

［1］波利亚.怎样解题［M］.涂泓，译.上海：上海科技教育出版社，2007.

［2］韩龙淑.数学教学中如何引导学生进行解题学习的反思［J］. 数学教学研究，2006（3）：7-9.

［3］孙朝仁.中考试题解法自然性的四个“引擎”［J］. 中国数学教育（初中版），2016（10）：54-55.

［4］郝晓鑫，韩龙淑.面积法在解中考数学试题中的运用［J］.中国数学教育（初中版），2016（10）：52-53.

［5］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2017—06—20

韩龙淑（1965—），女，教育学博士，太原师范学院教授，主要从事数学课程与教学论研究.