构造圆，“拔开云雾见月明”——“有公共斜边的直角三角形”模型的建构与应用

吴方建

（福建省尤溪县文公初级中学）

构造圆，“拔开云雾见月明”
——“有公共斜边的直角三角形”模型的建构与应用

吴方建

（福建省尤溪县文公初级中学）

2017年中考命题重视对学生发展性的评价，关注核心素养层次性的考查，数学抽象、数学建模、直观想象是数学学科核心素养的重要内容.文章以2017年质检卷、中考模拟卷中，选择题、填空题的压轴题的倒数第一题、倒数第二题中的一类题型为素材进行整合，抽丝剥茧，挖掘这类题型的共同特点，对核心图形进行探究，建构模型，实现“多题同解”，达到思路分析“化难为易”、解题过程“化繁为简”的效果.

公共斜边；直角三角形；构造圆；数学抽象；几何模型

中考复习中，对一类含有相同数学本质的试题进行整合，追根溯源，揭示图形的本质，归纳解决这类图形中问题的方法，并建构模型.既能让学生夯实基础，达到“知一形，晓一类”、以点破面的效果，同时也是以解决具体问题为载体，发展学生的数学核心素养.

一、题型呈现

例1 如图1，在△ABC中，AC=BC，∠ACB=90°，点D在BC的延长线上，连接AD，过点B作BE⊥AD，垂足为点E，交AC于点F，连接CE.

（1）求证：△BCF≌△ACD.

（2）猜想∠BEC的度数，并说明理由.

（3）探究线段AE，BE，CE之间满足的等量关系，并说明理由.

图1

图2

学生解题反馈（笔者重点聚焦第（2）小题）：绝大多数的学生能猜想出∠BEC=45°；在说理环节，第（2）小题结论的证明方法很多.例如，割长补短法.如图2，在BE上截取BE′=AE，利用第（1）小题的结论△BCF≌△ACD，可证△BCE′≌△ACE.由全等三角形的性质，得∠BCE′= ∠ACE，CE′=CE.又因为∠BCE′+ ∠FCE′=90°，等量代换，得∠FCE′+∠ACE=90°.因此，得△E′CE是等腰直角三角形.从而证得∠BEC=45°.

例2 如图3，已知点A（-8，0），点B（2，0），点C在直线上，则使△ABC是直角三角形的点C的个数为（ ）.

（A）1

（B）2

（C）3

（D）4

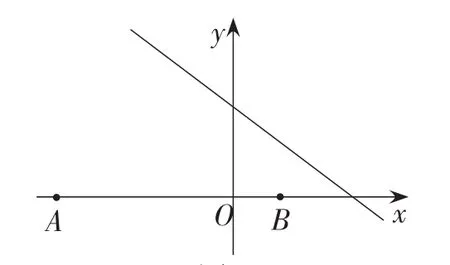
图3

学生解题反馈：此题分三种情况进行讨论，即直角顶点分别是点A，B，C三种情况，学生通过画图，易找到点A，B为直角顶点时，点C的个数分别为1个，点C为直角顶点时，点C的个数有几个？多数学生无法确定.

二、图形解析

综合例1、例2进行分析，例1中Rt∆ACB与Rt∆AEB有公共斜边AB；例2中点C为直角顶点时.由于点A，B是定点，所以点C是以AB为斜边的所有直角三角形的直角顶点.由此可见，例1、例2都含有相同的特定结构的图形，即“有公共斜边的直角三角形”.我们知道直角三角形的外接圆是以斜边为直径的圆.如果一些直角三角形都以某一线段（如线段AB）为斜边，那么这些直角三角形就会共圆，对于这类图形的问题，构造圆，常常可以收到“四两拨千斤”的效果.

例如，例1的第（2）小题，因为Rt∆ACB与Rt∆AEB有公共斜边AB，构造以AB为直径的圆，如图4所示.由同弧所对的圆周角相等，即可推出∠BEC=∠BAC=45°，与其他解法相比，显而易见，这种思路直观、简单.

图4

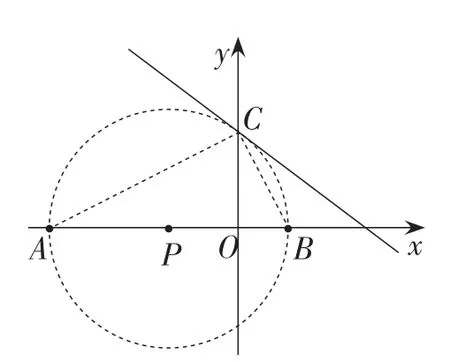
图5

又如，例2，当△ABC中C为直角顶点（即Rt∆ACB始终以AB为斜边）时，如果我们能从“有公共斜边的直角三角形”共圆角度分析，构造圆，问题就迎刃而解.如图5，平面内满足∠ACB=90°的所有点C组成的图形，是以AB为直径的⊙P；而点C又是直线上的点.因此，点C的个数是⊙P与直线交点的个数（或将问题转化为确定直线与圆的位置关系），通过画图（或计算）可得此情况时点C的个数是1.

由此可见，“有公共斜边的直角三角形”中的问题，构造圆，即可轻松“破题”，简化推理过程，减少、甚至省略计算.如何让学生在今后的解题中，善于发现图中“有公共斜边的直角三角形”，并能通过构造圆来解决问题呢？

三、建构模型

本模型的教学要做好三个方面：（1）熟练掌握图形的特点，善于在图中发现本模型；（2）理解图形的性质，能构造圆；（3）结合文本条件，辅以圆的知识，寻找解决问题的途径.

活动1：看图，说说你的发现.

几何画板软件动态演示：如图6，一条固定的线段AB，变化以AB为斜边的直角三角形的形状与位置.

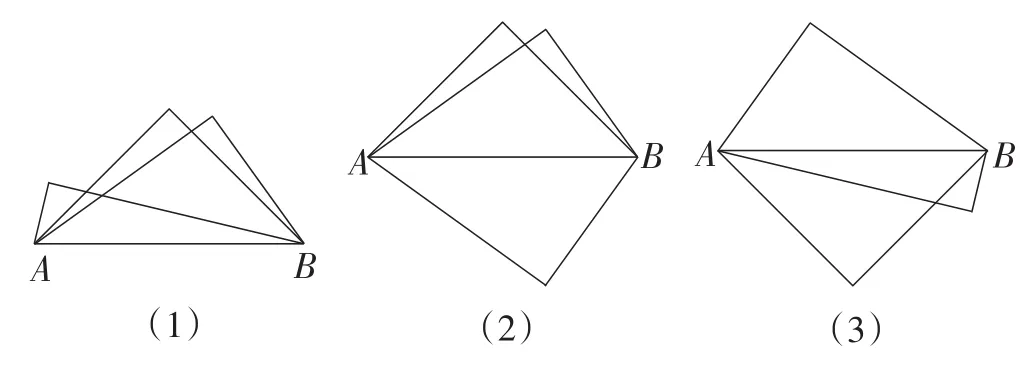
图6

【活动意图】通过几何画板软件动态演示如图6所示的情境，不断变化直角三角形的形状与位置，使学生比较全面、深刻、直观地认识有公共斜边的直角三角形的模型.提升学生在复杂图形中抽象出本模型的直观感知能力.

活动2：画图.

如图7，已知线段AB，画出平面内满足∠ACB=90°的所有点C组成的图形.

图7

图8

在学生完成画图（如图8）后，进行追问.

追问1：⊙O上各点都是使∠ACB=90°的点C吗？并说明理由.

追问2：⊙O外是否存在满足条件的点C，并说明理由.

追问3：⊙O内是否存在满足条件的点C，并说明理由.

追问4：在“活动1看图”中，除了发现变化的直角三角形始终都是以AB为直径外，我们还能发现什么？

【活动意图】画图是让学生发现“有公共斜边的直角三角形”具有共圆的性质.而此题画图需要学生联想到“直径所对的圆周角是90°”，但以此为依据画图，仅仅是对结论的一种猜想，并不能充分说明“以AB为斜边的所有直角三角形的顶点构成的图形，就是以AB为直径的圆（点A，B除外）”，因此，在画图后追加1，2，3问，旨在说明画图的正确性.4问的目的是，使学生发现与理解本模型有显性与隐性两种，并能将两种进行统一，加深对模型的全面认识与理解.

活动3：证图.

如图9，已知∠ACB=∠ADB=90°.

求证：A，B，C，D四点共圆.

【活动意图】本活动，从证明的角度得出“有公共斜边的直角三角形”共圆的性质，掌握了建构本模型的基本依据.也使学生在应用本模型解题时，能保证解题的严谨性.

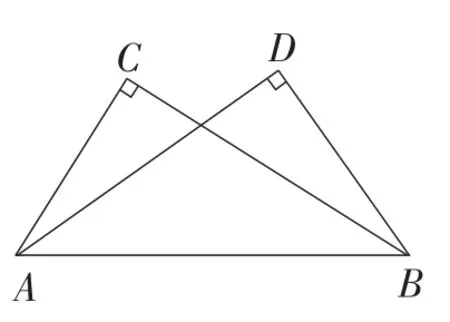
图9

四、模型应用

1.显性模型

例3 （2016年山东·青岛卷）如图10，在四边形ABCD中，∠ABC=∠ADC=90°，E为对角线AC的中点，连接BE，ED，BD，若∠BAD=58°，则∠EBD的度数为_______.

解析：由文本条件，可知Rt∆ABC 与 Rt∆ADC 有公共斜边AC.

由“有公共斜边的直角三角形”共圆的模型，可知A，B，C，D四点在以AC为直径的⊙E上（如图10）.

根据圆周角定理，可得∠BED=2∠BAD=116°.

又因为半径ED，EB相等，

所以△BED是等腰三角形.

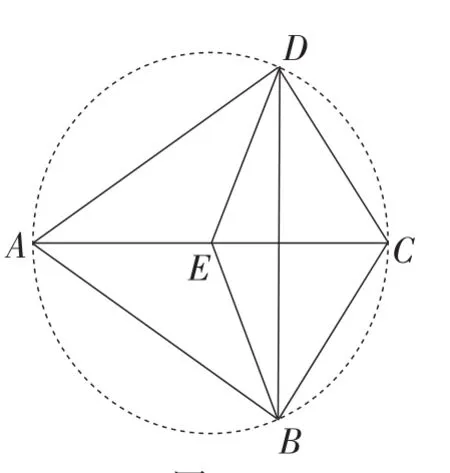
图10

2.半隐模型

（1）显直角隐公共斜边.

例4 （2017年福建卷）如图11，在矩形ABCD中，AB=6，AD=8，P，E分别是线段AC，BC上的点，且四边形PEFD为矩形.

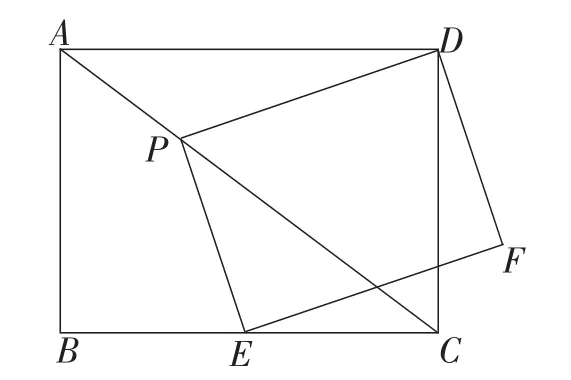
图11

（1）若△PCD是等腰三角形，求AP的长；

解析：如图12，此题聚焦第（2）小题，此题的主要思路是：证△CFD∽△APD，得.从而求得.

图12

从题干分析易证∠6=∠5.

而困难在于证∠1=∠4.

由图形可知，当点P，E分别在线段AC，BC上运动时，始终有∠EPD=∠EFD=∠ECD=90°.

连接DE，得到模型，构造以ED为直径的⊙O，

则P，E，C，F，D五点在⊙O上.

由已知条件及圆的相关知识可知，

因为PE=DF，∠3=∠1，∠3+∠2=90°，

所以∠1+∠2=90°.

因为∠4+∠2=90°，

所以∠1=∠4.

（2）显公共斜边隐直角.

（1）求m的值.

笔者聚焦第（2）小题：易求二次函数y=x2-4x，得A（0，0），B（4，0）. 因为点A，B是定点，又有∠ACB=90°，即“有公共斜边的直角三角形”模型，所以满足条件的点C都在以AB为直径的⊙P上（如图13（1））；点C又在直线上，由于直线的活动范围是直线y=-x向y轴正方向平移过程中任意时刻的情况.由图13（2）、图13（3）可知，直线在过原点的位置和直线与⊙P相切的位置之间时，直线与⊙P有公共点，此时直线存在满足条件的点C，故只需算出图13（3）中直线与圆相切时的b值，即可得b的取值范围.

图13

近几年在中考模拟、质检卷，以及中考试题中的选择题、填空题的压轴题和解答题的最后一两道题，常藏有“有公共斜边的直角三角形”模型，命题的立意是考查学生核心素养的层次性，重视对学生发展性的评价，需要学生综合运用知识解决问题.这些试题一般有多种解法，构造圆的方法少见；“有公共斜边的直角三角形”模型的应用，不仅呈现了“一题多解”，开拓学生思维，更是有集“抽象问题直观化”“烦琐过程简单化”“以不变应万变”展示“优化解题”“多题同解”的魅力.

波利亚在《数学的发现》中提出，数学离不开解题，解题的灵魂是数学思想，而数学模型是思想的载体.每一个几何图形中都蕴含着一定的规则，每一类题都有着相似的解题思想，同一类型的几何问题，采用相同的数学模型，使学生的思维过程形象化、程序化.这样，抽象、晦涩的几何问题变得更加简单、直观.对一些含有特定结构的几何图形，除去无用的部分，聚焦核心图形，引导学生探究核心图形的特点、内在的数学本质.让学生立足基础之上，在知识之间的交叉、渗透和综合中进行知识的再生、数学模型的建构、数学思想的感悟.从而体验数学知识的发生、发展和应用的过程，丰富学生的活动经验，提高学生的数学素养.

［1］沈岳夫.抓特征找规律 解一题会一类：对一道中考选择题求解的前思后想［J］.中国数学教育（初中版），2016（10）：21-25.

［2］李发勇.运用模型思想驱动几何解题有效思考：以一道几何题的多种解法探究为例［J］. 中国数学教育（初中版），2016（11）：45-47.

2017—06—01

吴方建（1974—），男，中学一级教师，主要从事初中数学教学研究.