借“题”发挥 借“力”拓展——一道中考几何题的变式与拓展

刘方剑

（浙江省江山市上余初中）

借“题”发挥 借“力”拓展
——一道中考几何题的变式与拓展

刘方剑

（浙江省江山市上余初中）

数学教学过程不仅是教材知识的传授，更重要的是学生学习能力和学习方法的培养.中考数学试题都是命题者用心设计、精心挑选的，充分挖掘中考试题的功能，借“题”发挥变式效应，并借“力”拓展训练，学生的思维定能达到严谨、深刻的境界，我们的课堂教学也就能收到意想不到的效果.通过对一道中考几何题的变式拓展，延伸出几个精彩鲜活的案例.

中考几何题；借题发挥；变式拓展

《义务教育数学课程标准（2011年版）》指出：学生的数学学习内容应当是现实的、有意义的、富有挑战性的，这些内容要有利于学生主动地进行观察、实验、验证、推理与交流等教学活动.内容的呈现方式应采用不同的表达方式，以满足多样化的学习需求.数学教学过程不仅是教材知识的传授，更重要的是学生学习能力和学习方法的培养.抓住典型习题，并借“题”发挥，借“力”拓展，灵活进行变式训练，才能满足学生的好奇心和求知欲，促使学生的思维向多方向、深层次发散，我们的课堂教学就能取得意想不到的效果.

下面笔者从一道中考几何题出发，进行有效的变式和拓展，与大家共赏.

题目 （2009年浙江·丽水卷）如图1，已知，在△ABC中，∠ABC=90°，AB=BC，三角形的顶点在互相平行的三条直线l1，l2，l3上，且l1，l2之间的距离为2，l2，l3之间的距离为3，则AC的长是（ ）.

（D）7

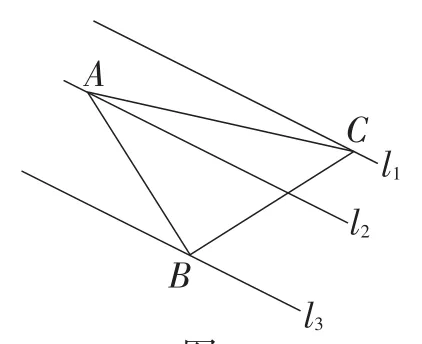
图1

分析：这是2009年浙江省丽水市中考试题，大家非常熟悉，解题难度不大，只需过点A，C分别作直线l3的垂线段，然后利用三角形全等和勾股定理求出等腰直角三角形的腰长，最后求出斜边长即可.

解：如图2，过点A，C分别作直线l3的垂线段AD，CE，垂足分别为点D，E.

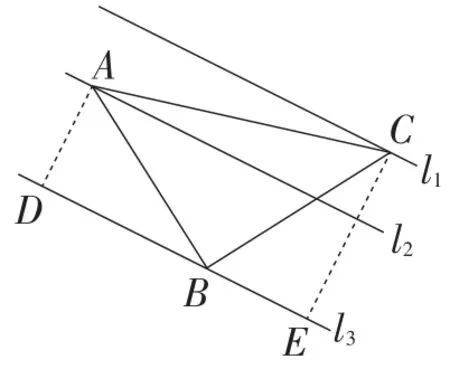
图2

因为∠ABC=90°，

所以∠ABD+∠CBE=90°.

因为∠CBE+∠BCE=90°，

所以∠ABD=∠BCE.

因为∠ADB=∠BEC=90°，AB=BC，

所以△ADB≌△BEC.

所以BE=AD=3.

故选A.

变式1：改变图形的位置.

例1 如图3，已知，在等腰Rt△ABC中，∠ACB=90°，AC=BC，三角形的顶点在互相平行的三条直线l1，l2，l3上，且l1，l2之间的距离为1，l2，l3之间的距离为2，求AB的长.

图3

分析：此题图形形状与原题一样，只是位置发生了改变，过点C作直线l1，l3的垂线段，构造全等三角形，运用全等三角形的性质和勾股定理即可求解.

解：如图4，过点C作CD⊥l1，CE⊥l3，垂足分别为点D，E.

因为∠ACB=90°，

所以∠ACD+∠BCE=90°.

因为∠CBE+∠BCE=90°，

所以∠ACD=∠CBE.

因为∠ADC=∠BEC=90°，AC=BC，

所以△ACD≌△CBE.

所以AD=CE=2.

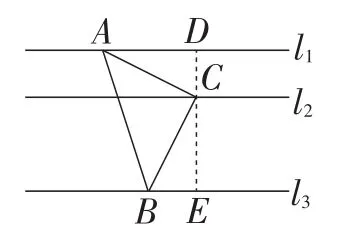
图4

【点评】例1中的等腰直角三角形顶点在直线l2上，而原题的等腰直角三角形顶点在直线l3上，所以变式出的例题与原题相比，只是图形位置不同，其他已知条件和求证结论基本相同，这种“神似形异”的变式训练，能满足学生的好奇心，提高学生学习数学的兴趣和热情.

学生通过变式训练，熟练掌握了同类型题目的解法，要求线段AB的长，首先要求等腰直角三角形的腰长.在此基础上，将题目按预设进行纵向拓展.

拓展训练：

例2 如图5，已知，在等腰Rt△ABC中，∠ACB=90°，AC=BC，三角形的顶点在互相平行的三条直线l1，l2，l3上，AC交直线l2于点D，且l1，l2之间的距离为1，l2，l3之间的距离为3，求BD的长.

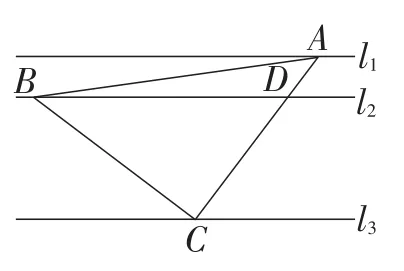
图5

分析：例2与原题的已知条件基本相同，只是求证的结论深度在原题基础上进行拓展，要求线段BD的长，只要求出CD的长即可，而要求出CD的长，顺理成章想到过点A，D作直线l3的垂线段，构造相似三角形，然后利用相似三角形的性质求出CD，再利用勾股定理求出BD的长即可.

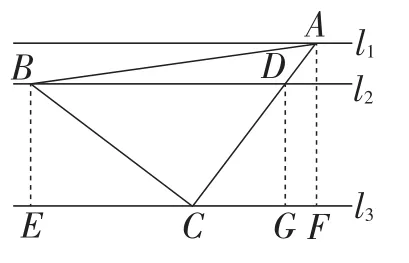
图6

解：如图6，过点A，B，D作AF⊥l3，BE⊥l3，DG⊥l3，垂足分别为点F，E，G.

因为∠EBC+ ∠BCE=90°，∠BCE+ ∠ACF=90°，

所以∠EBC=∠ACF.

因为BC=AC，∠BEC=∠CFA=90°，

所以△BCE≌△CFA.

所以CF=BE=3，CE=AF=3+1=4.

因为AF⊥l3，DG⊥l3，

所以△CDG∽△CAF.

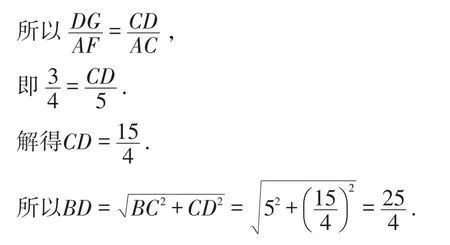
【点评】拓展训练对学生的解题能力提出了更高的要求，学生需要积累一定的类似题目的解题经验，构建相似三角形模型，综合运用相似三角形的性质、勾股定理等解决问题.

变式2：改变图形的角度.

例3 如图7，已知，在等腰△ABC中，∠ACB=120°，AC=BC，三角形的顶点在互相平行的三条直线l1，l2，l3上，且l1，l2之间的距离为1，l2，l3之间的距离为2，求AB的长.

图7

分析：例3只是将原题的条件“等腰三角形顶角∠ABC=90°”变为“等腰三角形顶角∠ACB=120°”. 表面上看解题难度有所增加，但只要认真思考，细心斟酌，还是能找到巧妙的解题方法.例如，延长BC至点D，使CD=CB，连接DA.过点B，D分别作三条平行线的垂线段，构造全等三角形和相似三角形，然后利用相似三角形的性质等求出AB的长.

解：如图8，延长BC至点D，使CD=CB，连接DA. 过点B作BE⊥l1，BH⊥l3，过点D作DF⊥l1，垂足分别为点E，H，F.DF交l3于点G.

因为∠ACB=120°，AC=BC，

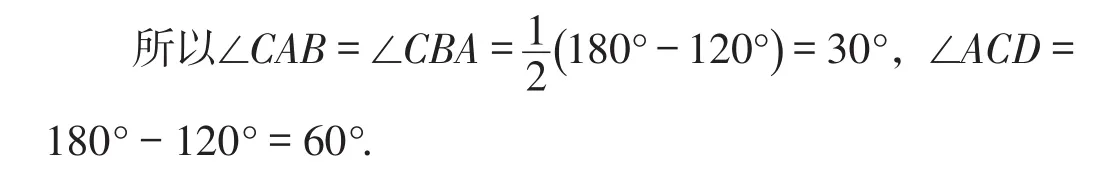
因为CD=CA，

所以△ACD是等边三角形.

所以∠CAD=60°.

所以∠BAD=90°.

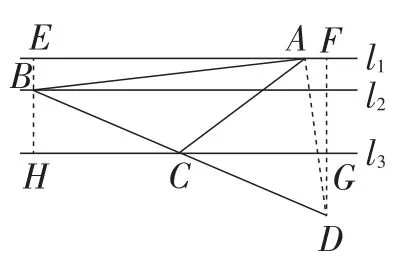
图8

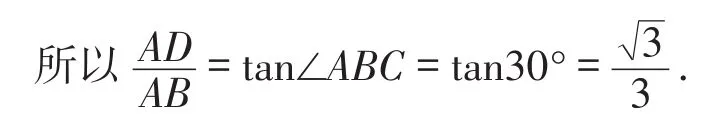
因 为 ∠BCH= ∠DCG， ∠BHC= ∠DGC=90°，CD=CB，

所以△BCH≌△DCG.

所以DG=BH=2.

所以DF=5.

由∠BAD=90°，得∠BAE+ ∠DAF=90°.

而∠ADF+∠DAF=90°，

所以∠BAE=∠ADF.

因为∠AFD=∠AEB=90°，

所以△AFD∽△AEB.

【点评】变式前的原题求解，大家普遍感觉比较简单，因为只需要利用三角形全等和勾股定理就可以解决问题，而三角形全等和勾股定理是学生需要熟练掌握的知识内容，其实变式后的例3求解也不烦琐复杂，它无非是巧妙构造全等三角形和相似三角形罢了.

拓展训练：

例4 如图9，l1，l2，l3是同一平面内的三条平行直线，l1与l2之间的距离是1，l2与l3之间的距离是2，正△ABC的三个顶点分别在l1，l2，l3上，求△ABC的边长.

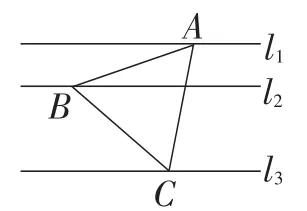
图9

分析：例4拓展训练将原题条件“等腰三角形顶角90°”改为“等腰三角形顶角60°”，即△ABC是等边三角形，思考复杂，难度较大.它需要巧妙地作点B关于直线l3的对称点D，然后综合利用轴对称性质、圆周角定理和勾股定理等巧妙求解.

解：如图10，作点B关于直线l3的对称点D，延长DB交直线l1于点F，连接AD，CD.

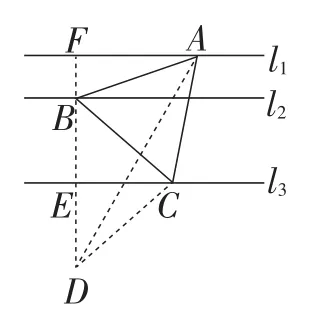
图10

因为CA=CB=CD，

所以点A，B，D在以点C为圆心，以CA为半径的圆上.

因为∠ACB=60°，

因为DF=2+2+1=5，

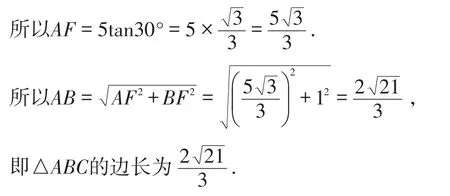
【点评】此题利用轴对称性质和圆周角定理求解，解法巧妙独特.当然此题方法有多种，如利用例3的解法也能轻松求解，读者不妨一试.它对训练学生思维的广阔性、灵活性和深入性都有较好的作用，是一道综合性较强的好题.

变式3：改变图形的形状.

例5 如图11，已知直线l1∥l2∥l3∥l4，相邻两条平行直线间的距离都是1，如果正方形ABCD的四个顶点分别在四条直线上，求sin a的值.

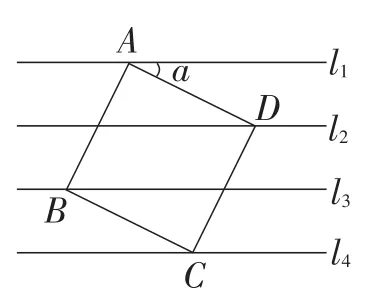
图11

分析：例5与原题相比，图形的形状发生了变化，即将原来的“等腰直角三角形”改变为“正方形”，并添加了三角函数知识，解法大同小异.过点D作直线l1，l4的垂线段，构造全等三角形，先利用勾股定理求出正方形的边长，再利用三角函数定义求出sin a的值.

解：如图12，过点D作EF⊥l1，交l1于点E，交l4于点F.

因为l1∥l2∥l3∥l4，

所以EF与l2，l3，l4都垂直.

因为∠ADC=90°，

所以∠ADE+∠CDF=90°.

又因为∠a+∠ADE=90°，

所以∠a=∠CDF.

图12

因为AD=CD，∠AED= ∠DFC=90°，

所以△ADE≌△DCF.

所以AE=DF=2.

【点评】此题变式求解，虽然在题目图形上有所变化，但解法难度不大，无非是在原题的基础上加入了三角函数知识，学生做完类似题目会感觉意犹未尽，如果能将此题继续拓展深入，将更多新、旧知识综合串联运用，学生方可解答尽兴.

拓展训练：

例6 如图13，已知直线l1∥l2∥l3∥l4∥l5，相邻两条平行直线间的距离相等且为1，如果四边形ABCD的四个顶点在平行直 线上，∠BAD=90°，AB=3AD，DC⊥l4，求四边形ABCD的面积.

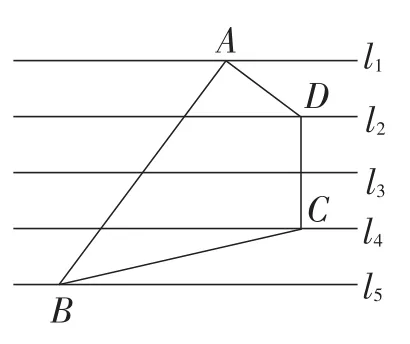
图13

分析：四边形ABCD是个不规则四边形，要求它的面积，只需要求出△ABD和△DBC的面积即可.将DC向两边延长，分别交直线l1，l5于点E，F，过点B作BH⊥l1，连接BD.利用△BAH∽△ADE，求出AH，AE的长，再利用勾股定理求出AB，AD的长.由于△DBC中DC边上的高线长即为HE的长，于是求出了△ABD和△DBC的面积，它们之和就是四边形ABCD的面积.

解：如图14，将DC向两边延长，分别交l1，l5于点E，F，过点B作BH⊥l1于点H，连接BD.

因为DC⊥l4，l1∥l2∥l3∥l4∥l5，

所以DC⊥l1，DC⊥l5.

所以∠BHA= ∠DEA=90°.

所以∠ABH+ ∠BAH=90°.

因为∠BAD=90°，

所以∠BAH+ ∠DAE=90°.

所以∠ABH=∠DAE.

所以△BAH∽△ADE.

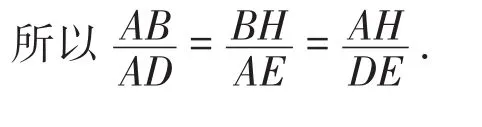
图14

因为AB=3AD，BH=4，DE=1，

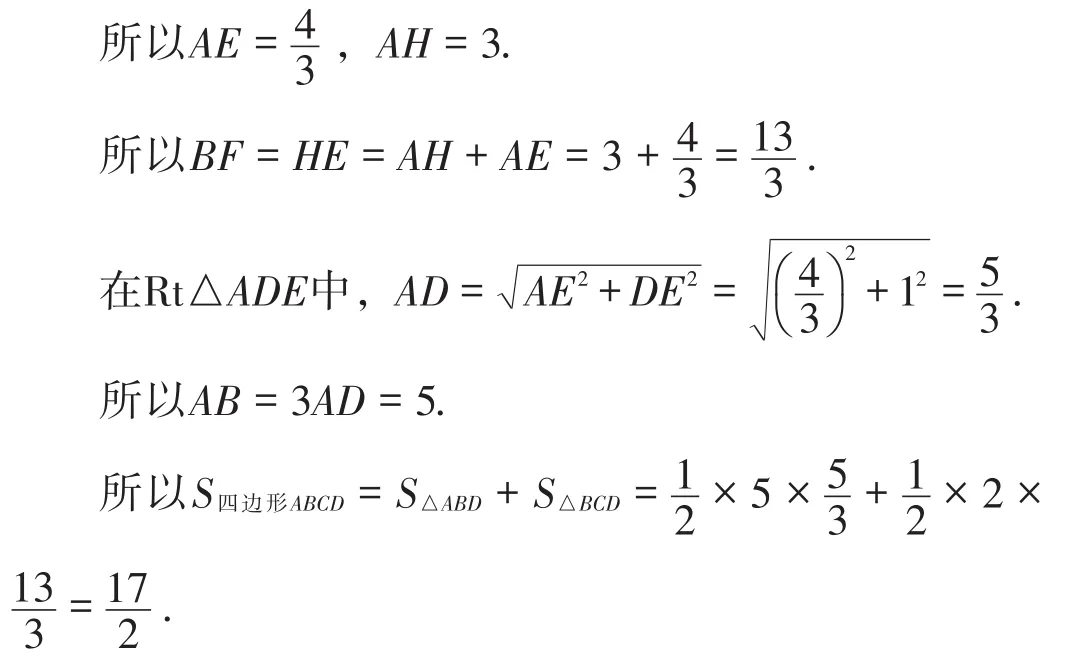
【点评】例6拓展训练将原来的规则图形即正方形改变为不规则四边形，初看会感觉无从下手，但从已知条件∠BAD=90°入手，根据上述变式题的解题经验，很快判断三角形相似，再根据三角形相似性质求出相应线段的长，问题便可迎刃而解.

一道普通的中考试题，能创造延伸出如此丰富多彩的变式拓展题，令人拍手叫绝！中考题、竞赛题，甚至教材中的例题、习题，都是命题者或编者用心设计、精心挑选的，是知识、技能、思想和方法运用联系的纽带，具有较高的开发价值.充分挖掘试题、例题、习题的功能，借“题”发挥变式效应，并顺势借“力”拓展训练，学生的数学思维定能达到严谨、深刻的完美境界，我们的课堂教学一定能锦上添花，大放异彩.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］吴晶君，刘海涛.基于变异理论的初中数学变式教学实践与思考［J］.中国数学教育（初中版），2015（7/8）：17-20.

［3］王华.关注概念形成，激活学生思维［J］.中国数学教育（初中版），2014（3）：36-40.

［4］王学先.2013年中考数学试题分类解析［J］.中国数学教育（初中版），2014（1/2）：43-62.

2017—04—24

刘方剑（1970—），男，中学高级教师，江山市数学学科带头人，主要从事初中数学教育教学研究.