依托实验教学 提升核心素养

陈海烽

（福建省厦门市五缘实验学校）

依托实验教学 提升核心素养

陈海烽

（福建省厦门市五缘实验学校）

“实验”是学生重要的学习方式之一，文章通过对初中数学概念的学习、数学公式的探究、数学定理的发现、数学规律的探索四个方面阐述了“实验教学”在课堂中的运用，通过引导学生进行操作实验，在此基础上培养学生的核心素养.

数学实验；数学概念；数学公式；数学定理；核心素养

《义务教育数学课程标准（2011年版）》（以下简称《标准》）指出：认真听讲、积极思考、动手实践、自主探索、合作交流等，都是学习数学的重要方式.在谈到“资源开发”时指出：教师应当努力开发制作简便实用的教具和学具，有条件的学校可以建立“数学实验室”供学生使用，以拓宽他们的学习领域，培养他们的实践能力，发展其个性品质与创新精神，促进不同的学生在数学上得到不同的发展.为了全面落实上述理念，更好地培养和提高学生的数学综合素养，我们应积极开展数学实验教学.

笔者研究发现，在初中课程中的多数数学概念、公式、定理、法则等具体知识的教学，根据具体的课程内容，精心设计实验问题，引导学生完成对这些核心知识的学习.

一、数学概念学习

数学概念是最重要的基础知识，概念明确是决定教学效果的重要因素，也是我们应贯穿整个课堂教学始终的因素.注重数学概念教学既是数学教学的重要环节，又是数学学习的核心.我们一直强调概念教学要经历过程，只有这样学生对概念的印象才能更加深刻，记忆长远.经历过程的手段之一就是动手实验.

案例1：一次函数概念的建立过程.

为了引导学生建立一次函数概念，我们可以引导学生进行下面的实验.

实验探究：

我们知道弹簧的长度与所受力的大小有关，为了测定一根弹簧的长度与所挂重物之间的函数关系，小凯设计了如图1所示的一个的装置.

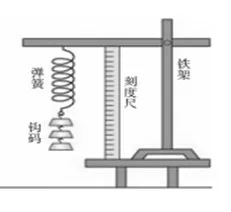
图1

首先把弹簧的上端固定在铁架的横臂上，把一个刻度尺垂直竖立在铁架台上面，并且量出弹簧下面不挂任何重物时的长度S0.然后在弹簧的下端挂上一个钩码，在钩码静止不动后，量出弹簧的长度S1.之后，依次在弹簧下端挂2个，3个，…，10个钩码时，同时测量出弹簧的长度S2，S3，…，S10，把得到的数据填写在表1中.

表1

思考与解答：

根据上述实验获得的数据进行思考，并解答下面的问题.

（1）如果设悬挂的钩码数量为n，弹簧长度用S表示，在弹簧的弹性限度内，随着n的逐渐增加，S将会怎样变化？

（2）钩码n每增加1个时，弹簧的长度S伸长了多少？

（3）你能直接写出弹簧长度S与钩码个数n之间的函数关系式吗？

【设计意图】本案例是在学生上节课学习了函数概念之后设计的，目的是为了引进了函数的概念.

学生通过实验，很容易得到表2中的数据.

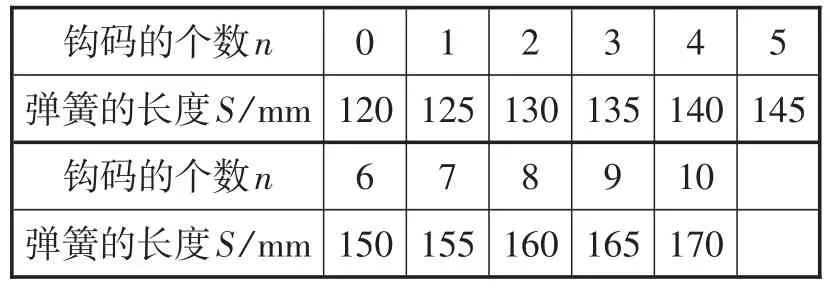
表2

并且根据上面的数据很容易得到前三个问题的答案，得出下面的结论.

（1）在弹簧的弹性限度内，当n逐渐增加时，S逐渐变大.

（2）每增加1个钩码，弹簧的长度S都会增加5 mm.

（3）弹簧的长度S与钩码的个数n之间函数的表达式是S=120+5n.

问题（4）的目的在于让学生概括出它们的共同特征：表达式都是自变量的一次式，都可以写成y=kx+b的形式.有了这样的认识，给出一次函数的概念就水到渠成了.

学生在做上述实验并探究建立函数模型的过程中，其数感、符号意识、运算能力、推理能力、模型思想等核心素养都将得到培养和发展.

二、数学公式探究

数学公式是重要的基础知识，很多数学公式都可以通过教师设计的问题情境，通过数学实验获取.学生在经历数学公式的推导过程中，不仅能获得公式，还能够加深对数学公式本质的理解.

案例2：一元二次方程求根公式的推导过程.

在目前所使用的数学教材中，对于一元二次方程的求根公式都是利用配方法推导出来的，其基本过程如下.

在代数学发展的初期，对于很多代数问题都是利用几何知识来解决的.今天看来，这样做有利于《标准》提出的“几何直观”素养的形成与培养.

古埃及是通过实验的方法，推导一元二次方程求根公式的.

问题的提出：

一个正方形与一个长方形的面积之和为c，其中长方形的一边长为b，另一边长等于正方形的边长，求此正方形的边长.

由于尼罗河的河水泛滥，每次洪水过后，原来土地的界线标志被损坏，测量人员需要重新丈量土地的面积，时间久了，便得到了利用“出入相补”的原理推导一元二次方程求根公式的方法.

问题的解决过程：

如图2，正方形的边长为x，长方形的长为x，宽为b.

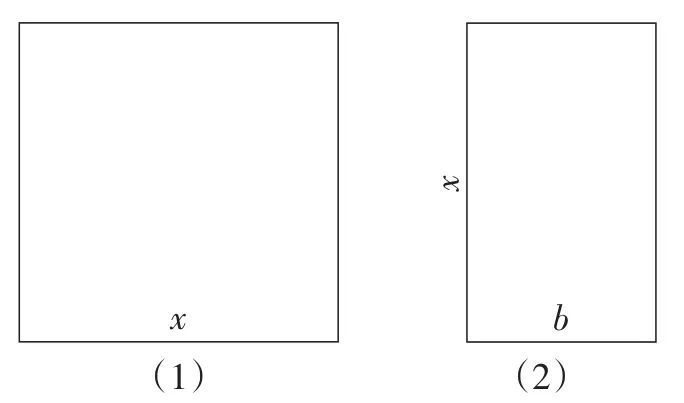
图2

如图3，把长方形平均分为两个面积相等的小长方形，同时，把一个小长方形拼放到图2的右边，另外一个放到图2的下面，并且在右下角补上一个边长等于的小正方形，于是得到一个边长为的大正方形，如图4所示.

图3

图4

根据题意，则有x2+bx=c，

即x2+bx=c的解为.

推广1：如何利用代数的方法解方程ax2+bx=c(a≠0)呢？

【设计意图】一元二次方程求根公式是《标准》界定的“数与代数”方面的重要基础知识，事实上，在代数学发展的初期阶段，许许多多的代数问题都是利用几何图形的知识来解决的.古埃及推导一元二次方程求根公式的方法的关键首先是分割图形——拼接图形；然后是利用图形的面积相等建立方程，进而推导出来的.这个过程从实验入手得到了一元二次方程求根公式，从数学思想方法的高度看，推导过程体现了数形结合的思想.数与形分别代表着《标准》界定的“数与代数”“图形与几何”中的部分内容，事实上，二者之间的内容是相互渗透的，教学中恰当的利用数形结合的思想能收到出奇制胜的效果.另外，推导过程还体现了转化与化归的思想.

三、数学定理发现

在数学中，一些重要的命题或公式就是定理，证明定理是数学教学中的重要活动.证明的过程对于各种数学能力的提高是非常重要的.初中数学中的一些重要定理，特别是有关图形与几何的定理都可以通过设置问题情境，引导学生通过数学实验而获取.

案例3：勾股定理的探究发现过程.

勾股定理是数学中的一个重要定理，在探究这个定理的过程中，学生的数学思考、探究，以及发现问题、解决问题的能力都将得到发展，对这个定理我们可以通过精心设计的系列问题，在经历数学实验的过程中自主探究得到.

（1）用绿色硬纸片剪8个如图5所示的完全相同的直角三角形，直角三角形的直角边为a，b，斜边为c；

（2）在纸上画出两个边长都是a+b的正方形；把所剪得的4个直角三角形按如图6所示的方式摆放在第一个正方形内；将另外的4个直角三角形按如图7所示的方式摆放在第二个正方形内.

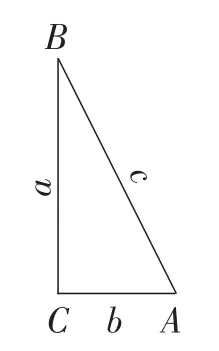
图5

图6

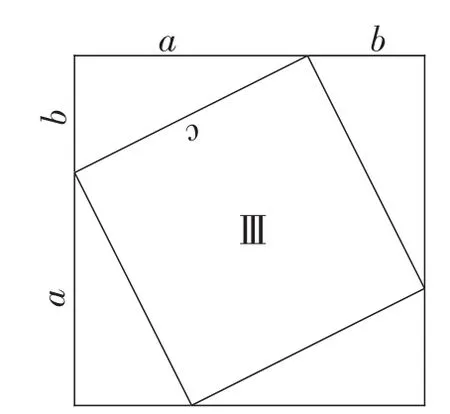
图7

（3）观察图6和图7中三个四边形Ⅰ，Ⅱ，Ⅲ的形状，并说明理由.

（4）判断图6中小正方形Ⅰ的面积是_______，小正方形Ⅱ的面积是_______，图7中小正方形Ⅲ的面积是_______.

（5）猜测三个小正方形Ⅰ，Ⅱ，Ⅲ的面积之间有什么关系？由此你有什么发现？

【设计意图】勾股定理的结论非常简洁.教学中如果直接把结论告诉学生，学生也一定能记住，但是这样的教学留给学生的只是一个数学符号而已，他们根本不知道学习这个定理的必要性，更为重要的是，课堂教学中放弃了一次培养学生探究学习的好机会.

为了让学生在自主探究的过程中发现勾股定理，并且经历实验、观察、计算、猜想、推理、验证等数学活动.我们设计了上面的一系列问题.引导学生在这些问题的探究中，通过动手操作、观察、比较等活动，自主探究到a2+b2=c2的结论，这个结论就是勾股定理.学生在探究的同时，不仅能获得勾股定理，还能体验到数形结合思想的作用，积累数学活动的经验.

四、数学规律探索

数学中存在大量的规律，其中很多规律，我们可以通过数学实验获得.

取一张大正方形硬纸片，设它的面积等于1.引导学生开展下面的折叠实验活动.

第1次双折叠，先把四边形对折一次得到长方形，再把长方形对折一次，这样就把大正方形纸片的面积四等分，则图8（1）中阴影部分的面积为；

第2次双折叠，把图8（1）中空白部分的长方形对折两次，这样就把长方形折叠成4个面积相等的小正方形，每1个小正方形的面积为，则阴影部分的面积为；

第3次双折叠，把上一次折叠图中空白部分的面积继续四等分，……；

……

第n次双折叠，把上一次折叠图中空白部分的面积最后四等分，所有阴影部分的面积之和为，最后空白部分的面积是，如图8（4）所示.

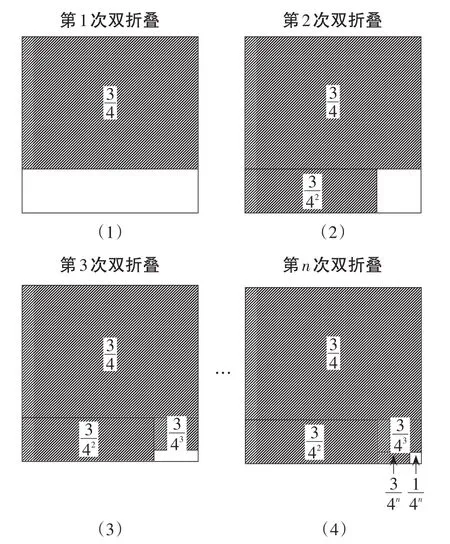
图8

在大部分数学概念、数学定理、数学公式的背后都存在一个几何“原型”，事实上，这种“原型”就是它们的本质特征，同时这些几何“原型”为我们进行实验教学提供了可能.学生在数学概念、定理、公式探究规律时，往往感觉很抽象，不好理解，究其根本原因就是没有利用好这些“原型”的直观作用.实践证明，对于这些知识的学习，我们都可以在认真研读课程内容的基础上，精心设置问题情境，以此引导学生在数学实验的过程中获取.学生在实验操作、思考探究、合作交流等过程中完成对这些知识的掌握.不仅如此，学生在实验的过程中还能形成数学的基本技能，感悟数学的基本思想方法，积累数学活动的经验，不断提高其数学核心素养.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］李树臣.实施问题解决策略 让学生真正会学习［J］. 中学教研，2014（12）：14-18.

2017—06—26

福建省教育科学“十三五”规划2016年度课题——依托数学实验提升学生数学核心素养的案例研究（FJJKXB16-176）.

陈海烽（1971—），男，中学高级教师，主要从事高效课堂和试题研究.