从几个教学片断谈概念教学立意的三个层次——观市优质课“分式”有感

张安军

（浙江省台州市白云中学）

从几个教学片断谈概念教学立意的三个层次
——观市优质课“分式”有感

张安军

（浙江省台州市白云中学）

数学概念课教学中，授课者的立意和教学目标定位不同，不同的教师会有不同的教学设计和教学效果.本研究采用一次市优质课评比中3节有代表性的同课异构进行分析.知其然——以知识为立意；知其所以然——以能力为立意；何由以知其所以然——以育人为立意.文章对概念教学的三个层次之间的关系以及如何提升概念教学的层次性提出了思考.

概念教学；课堂立意；教学片断

笔者有幸于2016年9月担任本市优质课评比的评委，其中一个比赛的课题是人教版《义务教育教科书·数学》八年级上册第15章“分式”的章起始课“从分数到分式”.多人中选取3节有代表性“从分数到分式”的同课异构进行分析，由于授课者的立意和教学目标定位不同，引发笔者对概念教学层次性的思考.

一、概念教学的三个层次

第1个层次：知其然——知识为立意（教师A的教学流程）

（1）类比分数，概念形成.

问题1：四张卡片分别写着2，3，a，b，从中任取若干张进行四则运算，你会得到哪些运算结果？

学生独立思考后，教师整理得到如下的代数式.

追问1：你能给上述中的式子按一定标准分类吗？

追问2：你能给这类新的式子取一个名字、下一个定义吗？

（2）概念辨析，再探新知.

①下列式子中，哪些是整式？哪些是分式？

（A）整式

（B）分式

（C）可能是整式，可能是分式

（D）既不是整式，也不是分式

x-1 xx

教师A让学生运用运算符号连接已有的数或字母，然后对这些代数式进行分类；代数式中一类是整式，另一类是“分式”，从而引入课题，再通过观察、比较、归纳、概括形成分式的概念.分式概念的引入看似快速有效，然而为什么要对数或字母进行四则运算，没有让学生经历自然、合理的发现或提出“分式”概念，对“分式”概念的产生、发展内在的逻辑没有追根溯源.在得到分式的概念后，马上进行概念的辨析.“分式”概念巩固后进行分式求值的练习，通过学生尝试性进行分式求值练习，得到了字母取何值时，分式的值为0、分式有意义和无意义.在这个求值过程中，教师仅仅让学生反复地进行模仿性、低层次的操练，分式的取值为0仅是分式的一个特殊值，由于分式的分母中含有字母，因此在取值时要注意分母不为0，这样分式才有意义.没有让学生体悟到字母取不同的值可以得到不同分式的值，从而体现“分式”比“分数”更具一般性.

上述教师A重视基础知识和基本技能的落实，及时巩固反馈，对于学生容易出错的问题，有针对性的强化训练，重在基础知识和基本技能的落实，重在概念的知识层面，概念教学仅停留在知其然的状态，重在知识立意.

第2个层次：知其所以然——能力为目标（教师B的教学流程）

（1）温故知新，概念引入.

问题1：对于整式及其运算，我们已经学习了整式的哪些运算？

（2）类比分数，概念形成.

问题2：一艘轮船在静水中的航速为30 km/h，它沿江顺流航行90 km所用的时间，与逆流航行60 km所用的时间相等，则水流的速度为多少？

问题3：完成下列问题.

（1）长方形的面积为10 cm2，长为7 cm，则宽为______.长方形的面积为S，长为a，则宽为______.

（2）把体积为200 cm3的水倒入底面积为33 cm2的圆柱形容器中，则水面高为______；把体积为V+3的水倒入底面积为S的圆柱形容器中，则水面高度为______.

问题4：下列6个式子有什么共同点？

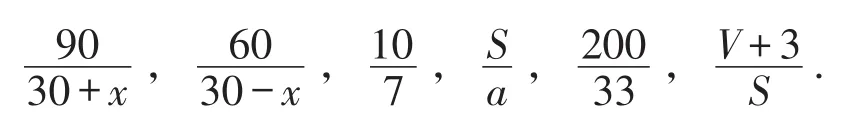
问题5：你能对这6个式子进行分类吗？你分类的标准是什么？

问题6：通过刚才的研究，你认为怎样的式子叫做分式？你能对分式下个定义吗？

问题7：类比分数的研究思路，你认为学习“分式”要学习哪些内容？

（3）概念辨析，再探新知.

教师B与教师A练习类似，只是在感悟分数和分式的关系时，教师B设计与教师A不同的如下的练习.

追问1：这些分数所对应的x的值是什么？从中你能体会到分数与分式的关系吗？

追问2：x能取0吗？x能取1吗？为什么？

追问3：你能得到分式有意义的条件吗？

教师B从“分式”的产生源头上进行回顾，类比整数的运算，对于整式又学习了哪些运算，让学生进行回顾，首先学习整式的加、减，而后学习整式的乘法，此时在学生的最近发展区中提出问题，“类比整数的运算，对于整式还要学习哪些运算？”分式在本质上是两个整式相除，且除数的整式中含有字母，对“分式”概念的产生不仅知其然，而且知其所以然，注重概念的产生与发展，重视概念的过程性教学.由于分式和分数在形式上类似，分式类比分数，开展数学中的章前课学什么，怎样学；分式是代数式的一种，教师以教材中提供的问题让学生感受分式在生活中也有广泛的应用，感悟学习“分式”的概念的必要性.当x取不同的数值，得到了不同的分式的值，字母取不同的数时，分式就有无数多个值与之对应，使学生体会到一般到特殊、抽象到具体的关系，感悟分式比分数更具一般性.在取值过程中，当字母取某一些数时，发现分式有意义；当字母取某一特定的值时，分母为0，分式无意义；当分式的值为0时等分式的特殊值；当学生理解分式有意义和无意义时，再进行相应的巩固和提升练习.

教师B与教师A比较而言，对知识的所以然进行追溯，注重学生的前概念，善于用类比的方法对新知识进行有效的迁移，在分式的求值过程中，让学生自然地感悟到分式比分数更具一般性，从而体会到学习分式的必要性.然而教师B仅从教材的编排上对“整式及其运算”进行了回顾，没有对“分式”的概念为何知其所以然进行追溯.第三，对于概念的产生、形成阶段，学生对什么是分式，还没有形成认识，此时课堂中要求学生对一组代数式进行分类，这就涉及到分式概念的内涵和外延的辨析，这不利于分式概念的抽象.

从上述分析可知，教师B在概念的教学中重视概念的过程性教学，能从课程的知识结构追溯概念的产生与发展，重视概念教学中所蕴涵的数学思想和方法，概念教学中不仅知其然，而知其所以然的层次．

第3个层次：何由以知其所以然——育人之道（教师C的教学流程）

（1）温故知新，概念引入.

（微视频）数的产生和发展离不开生活和生产的需要，由记数等产生数1，2，3，…，由表示“没有”，产生数0，两自然数相加或相乘还是自然数，但是两个自然数相除不一定是自然数，表现在日常生产和生活中的分物、测量等，于是产生了分数，如等.后来人们发现，用一个数减去一个较大的数，数就不够用，于是产生了负数.数学内在张力和现实生活的需要推动数的范围不断地扩大.

用字母表示数，是数学史上一次巨大的变革.我们已经学过整式，整式是数的进一步推广，数有运算，整式也有运算；两个整式的加、减、乘法，运算的结果都是整式，那么两个整式相除呢？结果还是整式吗？

（2）类比分数，概念形成.

问题1：取3，5，7三个整数中的两个进行“+”“-”“×”中的一种运算，你会得到哪些结果？

追问：这些结果都是什么数？

问题2：取上面三个整数中的两个进行“÷”运算，又会得到哪些结果？

追问：这些结果都是什么数？

问题3：更一般地记“5=a”，那么3和7分别表示a-2和a+2，对a，a-2和a+2中任取两个进行除法运算，并写出运算结果.

追问1：整式除法运算所得的结果都能用整式表示吗？

追问2：类比分数的结构特征，你能给这类式子取个名字并下一个定义吗？

分式这一章编者意图强调类比思想，强调数、式通性，数是式的具体体现，式是数的一般化；那么整式、分式相对于整数、分数，回忆分数是怎样产生的？类比数的产生，那么分式又是如何产生的？教师利用多媒体技术，图文并茂进行简短的回顾，即分数的产生一方面来自于数学外部，即生产和生活中的需要，客观上推动数学的进步.例如，在平均分配或者工程丈量时遇到不能分尽单位量，就产生了分数.另一方面是来自于数学内部，两个自然数进行加法、乘法，运算的结果还是自然数，也就是说自然数对加法和乘法运算是封闭的；但是两个自然数进行减法，运算的结果不一定是自然数，于是引入负数；同样两个整数进行除法，运算的结果不一定是整数，于是引入分数.类比数系的扩充，两个整式进行加法、减法、乘法运算，结果还是整式，但是两个整式进行除法运算，结果不一定是整式，于是产生了分式，从数学内部理清分式概念的产生，当然另一条主线来自于数学外部，生产和生活中有大量分式的实例.

从数到式，数式通性，类比整数到分数，两个整式相除可以得到分式，分式的实质是两个整式不能整除时，结果用分式表示，可见分式从形式上看类似于分数，都有分数线；从分式产生的角度看，是因为两个整式进行除法运算.这样通过提供多个类比源或者进行多次类比，可以使学生感受到分式概念认知图式.

从上述分析可知，教师C概念教学不仅停留在知其所以然，而且为何知其所以然，从它的背景、形成过程，以及与其他概念的联系中感受到分式概念的起源是那么自然而合理.不仅让学生体会从数到字母及整式，是数学史上的一大进步，而且让学生感受到从分数到分式是数学逻辑内在使然，分式比分数更具一般性.同时该教师在后继的教学中列举生产和生活中分式的实例，从中在数学内部和外部感受学习分式的必要性.在概念中渗透数学思想和方法，既关注了学生的眼前利益，又注重学生的长远发展，充分体现了以学生终身发展为目标，从而实现了课堂教学的育人价值，达到教学的育人之道.

二、对概念教学三个层次的思考

中国近代数学教育家傅种孙在《高中平面几何》序中说过，几何之务，不在知其然，而在知其所以然；不在知其所以然，而在何由以知其所以然.傅先生说的虽然是几何教学的三个层次，事实上用在数学概念教学中也未尝不可.教师在概念教学的过程中，对概念教学的第一个层次是“知其然”，只知概念是什么，不知为什么，没有对概念的来龙去脉进行追根溯源；第二个层次是“知其所以然”，不仅知道概念的要义是什么，而且揭示概念的发生过程为什么是这样，第二个层次的教学是在第一个层次概念的教学的基础上的进一步发展和提升；第三个层次是“何由以知其所以然”，讲究概念的重构（再发现、再发明），亲历概念（可能）的生长过程，揭示概念定义构想、发现或发明的大致过程，以及相关数学思想方法的脉络；概念教学中既见树木又见森林，将原有的概念置于新的认知图景中，对概念的认识和理解置于数学整体的高度去理解，从而达到文化、美学的欣赏，具有创造性的理解.概念第三个层次不仅包含前两个层次的教学，而且它是前两个层次概念的进一步发展和升华.

每一个层次的概念教学都有其独特的价值和作用.例如，第一个层次概念教学能让学生理解概念是什么，理解概念的本质属性，对典型实例以及与若干其他对象之间的差异，能对概念与自我已有的相关数学概念之间建立本质上的联系，扩展知识网络，它是其他两个层次概念的基础.

日常概念教学中，如何进行高层次的概念教学设计呢？概念教学层次提升的前提是教师应有明确的追求高远立意的意识.古人云，取法乎上，仅得其中；取法乎中，仅得其下.教师在教学设计时应有追求高立意的意识，只有这样，在教学实施时才有可能有高质量、高效益的课堂.这就要求我们教师自己对教师的职业有较强的认同感，对自己的课堂教学怀着崇高的敬意和追求，在追求过程中不断提升教学理念.

其次，数学概念教学层次的提升，关键在于章建跃先生所倡导的读懂“三个理解”，特别是“理解数学”，高层次数学概念教学要求教师自己对数学本身有透彻的理解，能在更宽的领域里进行居高临下的观察，多角度地思考原有的概念和问题，达到一种新的思维水平.

挖掘数学概念所蕴涵的思想及其方法，以提高数学素养、发展思维能力、培育理性精神为核心，使学生在数学概念的形成过程中学会思考，成为善于认识问题、解决问题的人才.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.

［3］石树伟.数学课堂教学立意的“层次”“关系”及“提升”［J］. 数学教育学报，2013（1）：74-76.

［4］傅种孙.高中平面几何（第四版）［M］.北京：北京师范大学出版社，1982.

2017—05—07

张安军（1975—），男，中学高级教师，浙江省台州市名师，主要从事初中数学教学研究.