三角形中半角正弦和下界的一个猜想的证明

山东省威海职业学院信息工程系(264210) 姜卫东

三角形中半角正弦和下界的一个猜想的证明

山东省威海职业学院信息工程系(264210) 姜卫东

设△ABC的三边长分别为a,b,c,半周长为s,外接圆和内切圆半径分别为R,r.则有熟知的不等式[1]

引理1[2]在非钝角三角形中,有

引理2[3]内是减函数,在上为增函数.

(2)式的证明 由三角形中已知的恒等式

代入(2),得到如下的等价式

对(3)式作角变换

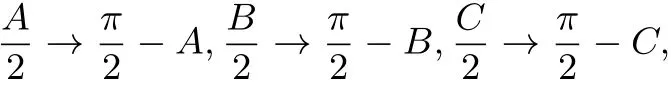
可知(3)等价于:在锐角三角形ABC中,

再由熟知的恒等式:

可知不等式(4)等价于

对(5)变形,可知只要证明下面的

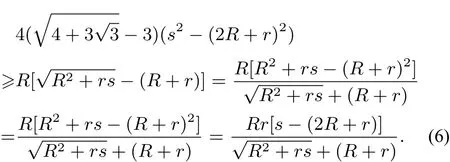
即可.注意到在锐角△ABC中,有s＞2R+r(见[1]P.123),要证(6),只需证

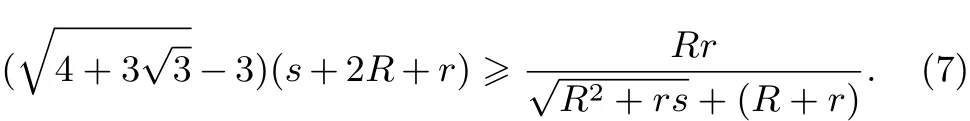
从而,要证(7),只要证明如下较强的不等式

由引理1可知,只需证

引入函数

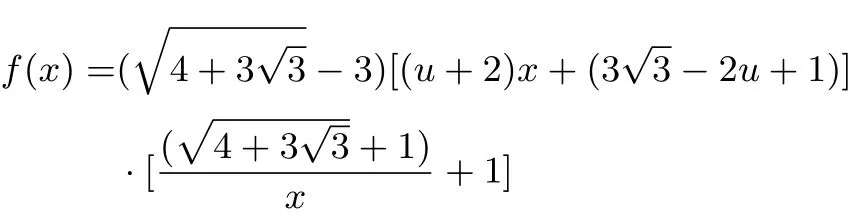
其中

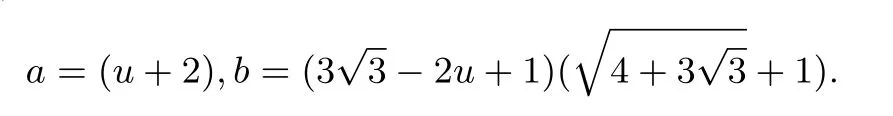
经简单计算,可得

再由引理2可知,f(x)在[2,∞)为增函数.从而f(x)≥f(2)=1,即(11)成立,从而猜想(2)成立.

致谢 本文受威海职业学院科研项目基金资助,编号2016ky001.

[1]O.Bottema等著,单墫译.几何不等[M].北京大学出版社,1991,9.

[2]杨学枝,尹华焱.我国研究三角形中半角三角函数不等式情况综述[C].杨学枝主编,不等式研究(第1版),西藏人民出版社,2000,6.

[3]胡长好.“对钩”函数的单调性及其运用[J].数理化学习,2013(1).